当前位置：首页 > news >正文

Lc 大数运算--快速幂 | 统计好数字的数目

news 来源：原创 2025/9/10 9:59:45

快速幂算法是一种高效计算大数幂运算的方法，能将时间复杂度从传统算法的O(n)降低到O(log n)。它的核心思想是 分解指数+分治思想，类似生活中的「拆快递」—— 把大包裹拆成小份，分批处理更高效。

一、生活示例：存钱罐的复利计算

假设你有一个每天利息翻倍的存钱罐：

第1天：本金1元 → 总金额 1元
第2天：1元变2元 → 总金额 2元
第4天：2元变4元 → 总金额 4元
第8天：4元变8元 → 总金额 8元

若想计算 第10天 的总金额，传统方法是连乘10次（1×2×2×2…），但快速幂会这样算：

拆解天数：10天 = 8天 + 2天（二进制：1010）
分步计算：

- 先算8天的金额：8元
- 再算2天的金额：2元

合并结果：8元 × 2元 = 16元

这种「拆分指数+复用中间结果」的方式，就是快速幂的核心

二、算法原理与代码实现

1. 二进制分解思想

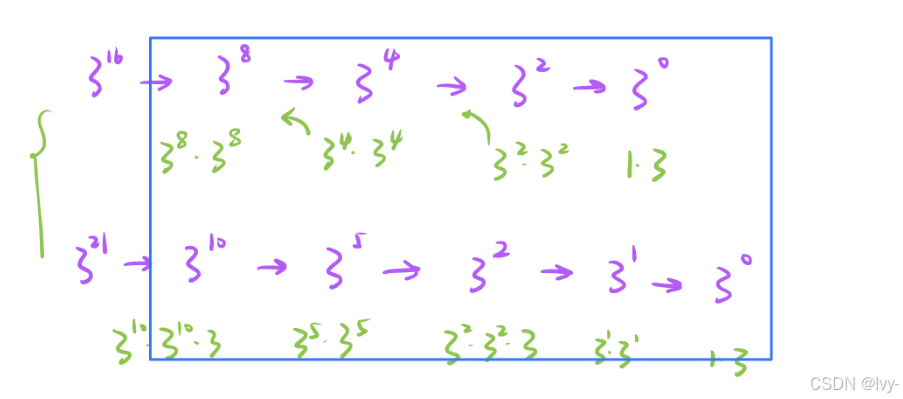
将指数看作二进制数，每一位代表是否需要乘当前底数的幂。例如计算3^5：

5的二进制是101 → 对应3(4+1) = 34 × 3^1
通过右移和底数平方逐步缩小指数规模

2. C++代码实现（位运算优化）

// 快速幂计算 a^b % mod
long long fastPow(long long a, long long b, long long mod) {long long res = 1;a %= mod; // 防止a过大while (b > 0) {if (b & 1) res = (res * a) % mod; // 当前二进制位为1时累乘a = (a * a) % mod; // 底数平方b >>= 1; // 右移一位（相当于b /= 2）}return res;
}

代码解析：

b & 1：判断二进制末位是否为1（奇偶性）
b >>= 1：指数右移，相当于除以2
a = a * a：底数平方，复用中间结果

三、对比传统方法

假设计算2^10：

传统方法：2×2×2×2×2×2×2×2×2×2 → 10次乘法
快速幂：

- 2^2 → 4（1次乘法）
- 4^2 → 16（第2次）
- 16^2 → 256（第3次）
- 256×16=4096（第4次）
  仅需4次乘法，效率显著提升

四、递归实现（分治思想）

分奇数偶数 return

long long fastPowRecur(long long a, long long b) {if (b == 0) return 1;long long half = fastPowRecur(a, b/2);if (b % 2 == 0) return half * half;else return half * half * a;
}

原理：将ab分解为a(b/2)×a^(b/2)，若b为奇数则额外乘a

五、应用场景

密码学：RSA加密中的大数模幂运算
动态规划：矩阵快速幂求解斐波那契数列
竞赛编程：处理1e18级别的指数运算

通过这种「化整为零」的思想，快速幂算法将复杂的幂运算转化为高效的位操作，如同把大任务拆解成小步骤分批完成，是算法优化中的经典范例。

1922. 统计好数字的数目

我们称一个数字字符串是 好数字 当它满足（下标从 0 开始）偶数下标处的数字为偶数且奇数下标处的数字为质数（2，3，5 或 7）。

比方说，"2582" 是好数字，因为偶数下标处的数字（2 和 8）是偶数且奇数下标处的数字（5 和 2）为质数。但 "3245" 不是好数字，因为 3 在偶数下标处但不是偶数。

给你一个整数 n ，请你返回长度为 n 且为好数字的数字字符串总数。由于答案可能会很大，请你将它对 109 + 7 取余后返回 。

一个 数字字符串 是每一位都由 0 到 9 组成的字符串，且可能包含前导 0 。

示例 1：

输入：n = 1
输出：5
解释：长度为 1 的好数字包括 "0"，"2"，"4"，"6"，"8" 。

示例 2：

输入：n = 4
输出：400

示例 3：

输入：n = 50
输出：564908303

提示：

1 <= n <= 10^15

数据很大时，我们就能想到快速幂了

模运算满足以下性质：
（a*b) mod m =[(a mod m) *(b mod m)] mod m
这意味着，在计算幂的过程中，每一步乘法后都可以立即取模，保持中间结果始终在合理范围内。
偶数位共有5种取值方式：0 2 4 6 8 。所以 len_even即有 5exp{len_even}
同理奇数位共有四种取值方式 2 3 5 7 。所以共有 4exp{len_odd}

一、题目分析

核心条件：

偶数下标（0,2,4...）必须是 0/2/4/6/8（共5种选择）。
奇数下标（1,3,5...）必须是 2/3/5/7（共4种选择）。

总组合数公式：
设字符串长度为 n：

偶数下标有 even = (n + 1) / 2 个位置 → 每个位置5种选择 → 总可能数为 5^even。
奇数下标有 odd = n / 2 个位置 → 每个位置4种选择 → 总可能数为 4^odd。
最终结果为 (5^even * 4^odd) % MOD（MOD=1e9+7）。

由于 n 最大为 1e15，直接计算幂会超时，必须用快速幂

二、生活实例：密码锁的排列组合

想象一个特殊的密码锁，长度为 n，每位数字有不同限制：

偶数位（如第0、2、4位）必须用 0/2/4/6/8（类似密码锁的“偶数环”）。
奇数位（如第1、3位）必须用 2/3/5/7（类似“质数环”）。

要计算所有可能的密码组合，传统方法是逐个计算每个环的可能性并相乘。但当锁的长度极大时（如1e15位），逐个计算显然不可行。
快速幂的作用：将指数分解为二进制位，通过“平方翻倍”的方式，像快速拆解密码环一样，大幅减少计算步骤

三、快速幂算法实现

1. 快速幂函数

long long fastPowRecur(long long a, long long b) {if (b == 0) return 1;long long half = fastPowRecur(a, b/2);if (b % 2 == 0) return half * half;else return half * half * a;
}

2. 主函数逻辑

int countGoodNumbers(long long n) {long long even = (n + 1) / 2; // 偶数位个数long long odd = n / 2;        // 奇数位个数long long part1 = fastPow(5, even); // 5^even % MODlong long part2 = fastPow(4, odd);  // 4^odd % MODreturn (part1 * part2) % MOD; // 合并结果
}

示例验证：

n=1 → even=1, odd=0 → 5^1 * 4^0 = 5 ✔️
n=4 → even=2, odd=2 → 5^2 *4^2=25*16=400 ✔️

四、快速幂如何优化计算？

以 5^4 为例：

传统计算：5*5*5*5=625（3次乘法）。
快速幂：

- 5^1 = 5
- 5^2 = (5^1)^2 = 25（1次平方）
- 5^4 = (5^2)^2 = 625（第二次平方）
  仅需2次平方操作，时间复杂度从 O(n) 降到 O(log n)

五、复杂度分析

时间复杂度：O(log n)，快速幂的二进制分解使指数规模每次减半。
空间复杂度：O(1)，仅用常数空间存储中间结果 [6] [12]。

通过快速幂算法，我们将原本需要 O(n) 时间的幂运算优化到 O(log n)，完美解决了大数取幂的问题。这种“分治+复用中间结果”的思想，如同拆解密码锁的环一样，将复杂问题高效拆解，是算法竞赛中的经典技巧。

class Solution {typedef long long ll;
const int mod=1e9+7;public:
ll fastpow(ll a,ll b)
{if(b==0) return 1;ll half=fastpow(a,b/2);//!!!!要分奇偶if(b%2==0) return half*half%mod;elsereturn half*half*a%mod;
}int countGoodNumbers(long long n) 
{ll ret=0;ll even=(n+1)/2;//oull odd=n/2;//jill part_ou=fastpow(5,even);//偶数可能：0 2 4 6 8//偶数位数：evenll part_ji=fastpow(4,odd);return (part_ji*part_ou)%mod;
}
};

数据规模挺大，使用快速幂时，记得乘一次就取余一次