5.4学习记录

今天的目标是复习+刷过往的提高课的DP题目：重点是数位DP，状态压缩DP，然后去做一些新的DP题目

然后明天的任务就是把DP的题目汇总，复习一些疑难的问题

方格取数：

题目背景

NOIP 2000 提高组 T4

题目描述

设有 N×N 的方格图 (N≤9)，我们将其中的某些方格中填入正整数，而其他的方格中则放入数字 0。如下图所示（见样例）:

某人从图的左上角的 A 点出发，可以向下行走，也可以向右走，直到到达右下角的 B 点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字 0）。
此人从 A 点到 B 点共走两次，试找出 2 条这样的路径，使得取得的数之和为最大。

输入格式

输入的第一行为一个整数 N（表示 N×N 的方格图），接下来的每行有三个整数，前两个表示位置，第三个数为该位置上所放的数。一行单独的 0 表示输入结束。

输出格式

只需输出一个整数，表示 2 条路径上取得的最大的和。

一次的走法：

f[i1][j1][i2][j2] 表示两个路径，从(1,1)走到(i1,j1),从(1,1)走到(i2,j2)

什么时候两个路径会重合尼？：

显然当他们重合的时候有i1+j1==i2+j2这个是很显然的

所以我们可以用k表示总步数

f[k][i1][i2]表示我们需要考虑的情况（其他状态下一步他们两个一定不会重合）

j1=k-i1    j2=k-i2

下面看我们的状态转移的方程：
四个推广的方向：
1下2下，1下2右，1右2右，1右2下

当然要判断一下这两个点走完过后不能够到同一个位置

如果重合的话，只加一次w(i,j)

如果没有重合的话，就要加上两次

代码：

#include<bits/stdc++.h>

using namespace std;

const int N=15;

int w[N][N];

int f[N*2][N][N];

int n;

int main(){

    cin>>n;

    while(1){

        int x,y,c;

        cin>>x>>y>>c;

        if(x==0&&y==0&&c==0)break;

        w[x][y]=c;

    }

    for(int k=2;k<=2*n;k++){

        for(int i=1;i<=n;i++){

            for(int j=1;j<=n;j++){

                int ii=k-i;

                int jj=k-j;

                if(ii<1||jj<1)continue;

                if(ii>n||jj>n)continue;

                int val=w[i][ii];

                if(i!=j)val+=w[j][jj];

                f[k][i][j]=max(f[k][i][j],f[k-1][i-1][j-1]+val);

                f[k][i][j]=max(f[k][i][j],f[k-1][i][j-1]+val);

                f[k][i][j]=max(f[k][i][j],f[k-1][i][j]+val);

                f[k][i][j]=max(f[k][i][j],f[k-1][i-1][j]+val);

            }

        }   

    }

    cout<<f[2*n][n][n];

}

导弹防御系统：

为了对抗附近恶意国家的威胁，RR 国更新了他们的导弹防御系统。

一套防御系统的导弹拦截高度要么一直 严格单调 上升要么一直 严格单调 下降。

例如，一套系统先后拦截了高度为 33 和高度为 44 的两发导弹，那么接下来该系统就只能拦截高度大于 44 的导弹。

给定即将袭来的一系列导弹的高度，请你求出至少需要多少套防御系统，就可以将它们全部击落。

输入格式

输入包含多组测试用例。

对于每个测试用例，第一行包含整数 nn，表示来袭导弹数量。

第二行包含 nn 个不同的整数，表示每个导弹的高度。

当输入测试用例 n=0n=0 时，表示输入终止，且该用例无需处理。

输出格式

对于每个测试用例，输出一个占据一行的整数，表示所需的防御系统数量。

代码：

#include<bits/stdc++.h>

using namespace std;

const int N=55;

int a[N];

int n;

int up[N];

int down[N];

int ans=0x3f3f3f3f;

void dfs(int pos,int pu,int pd){

    if(pu+pd>=ans)return;

    if(pos==n+1){

        ans=min(ans,pu+pd);

        return;

    }

    

    //放入上升序列

    int k=0;

    while(k<pu&&a[pos]<=up[k])k++;

    int back=up[k];

    up[k]=a[pos];

    if(k>=pu){

        dfs(pos+1,pu+1,pd);

    }else dfs(pos+1,pu,pd);

    up[k]=back;

    

    //放入下降序列

    k=0;

    while(k<pd&&a[pos]>=down[k])k++;

    back=down[k];

    down[k]=a[pos];

    if(k>=pd){

        dfs(pos+1,pu,pd+1);

    }else dfs(pos+1,pu,pd);

    down[k]=back;

}

int main(){

    while(scanf("%d",&n),n!=0){

        for(int i=1;i<=n;i++)scanf("%d",&a[i]);

        ans=0x3f3f3f3f;

        memset(up,0,sizeof up);

        memset(down,0,sizeof up);

        dfs(1,0,0);

        cout<<ans<<endl;

    }

}

最长公共子序列：

（融合了LIS的nlogn的LCS）

题目描述

给出 1,2,…,n 的两个排列 P1​ 和 P2​ ，求它们的最长公共子序列。

输入格式

第一行是一个数 n。

接下来两行，每行为 n 个数，为自然数 1,2,…,n 的一个排列。

输出格式

一个数，即最长公共子序列的长度。

#include<iostream>

#include<cstdio>

using namespace std;

int a[100001],b[100001],map[100001],f[100001];

int main()

{

int n;

cin>>n;

for(int i=1;i<=n;i++){scanf("%d",&a[i]);map[a[i]]=i;}

for(int i=1;i<=n;i++){scanf("%d",&b[i]);f[i]=0x7fffffff;}

int len=0;

f[0]=0;

for(int i=1;i<=n;i++)

{

int l=0,r=len,mid;

        int ans=0;

if(map[b[i]]>f[len])f[++len]=map[b[i]];//f存的是长度为i的最后一个数的位置，如果和b[i]相等的a[i]，可以接在最长的len后面

else //不能接在最后面，就找到所有已有长度中最长的，满足f[ans]<map[b[i]],以此去更新f[ans+1]

{

while(l<=r)

{

    mid=(l+r)/2;

    if(f[mid]>map[b[i]]){//不能接在后面

                r=mid-1;

            }

else if(f[mid]<map[b[i]]){//可以接在f[mid]后面，去找找更长的

                ans=mid;

                l=mid+1;

            }

}

f[ans+1]=min(map[b[i]],f[ans+1]);//可以接在ans后面，尝试去更新ans+1长度的最后一个值的更小的位置

      }

    }

    cout<<len;

    return 0;

}

最长上升子序列：

题目描述

这是一个简单的动规板子题。

给出一个由 n(n≤5000) 个不超过 106 的正整数组成的序列。请输出这个序列的最长上升子序列的长度。

最长上升子序列是指，从原序列中按顺序取出一些数字排在一起，这些数字是逐渐增大的。

输入格式

第一行，一个整数 n，表示序列长度。

第二行有 n 个整数，表示这个序列。

#include <bits/stdc++.h>

using namespace std;

const int N=5010;

int n;

int a[N];

int f[N];

int main(){

    cin>>n;

    for(int i=1;i<=n;i++){

        scanf("%d",&a[i]);

    }

    int len=0;

    memset(f,0x3f,sizeof f);

    f[0]=0;

    for(int i=1;i<=n;i++){

        int l=0,r=len;

        int ans=0;

        if(f[len]<a[i])f[++len]=a[i];//可以接在最后面

        else{//尝试优化内部结构

            while(l<=r){

                int mid=(l+r)/2;

                if(f[mid]>=a[i]){

                    r=mid-1;

                }else if(f[mid]<a[i]){

                    ans=mid;

                    l=mid+1;

                }

            }    

            //可以接在ans的后面

            f[ans+1]=min(f[ans+1],a[i]);

        }

    }

    

    cout<<len;

}

货币系统：

题目背景

NOIP2018 提高组 D1T2

题目描述

在网友的国度中共有 n 种不同面额的货币，第 i 种货币的面额为 a[i]，你可以假设每一种货币都有无穷多张。为了方便，我们把货币种数为 n、面额数组为 a[1..n] 的货币系统记作 (n,a)。

在一个完善的货币系统中，每一个非负整数的金额 x 都应该可以被表示出，即对每一个非负整数 x，都存在 n 个非负整数 t[i] 满足 a[i]×t[i] 的和为 x。然而， 在网友的国度中，货币系统可能是不完善的，即可能存在金额 x 不能被该货币系统表示出。例如在货币系统 n=3, a=[2,5,9] 中，金额 1,3 就无法被表示出来。

两个货币系统 (n,a) 和 (m,b) 是等价的，当且仅当对于任意非负整数 x，它要么均可以被两个货币系统表出，要么不能被其中任何一个表出。

现在网友们打算简化一下货币系统。他们希望找到一个货币系统 (m,b)，满足 (m,b) 与原来的货币系统 (n,a) 等价，且 m 尽可能的小。他们希望你来协助完成这个艰巨的任务：找到最小的 m。

输入格式

输入文件的第一行包含一个整数 T，表示数据的组数。

接下来按照如下格式分别给出 T 组数据。 每组数据的第一行包含一个正整数 n。接下来一行包含 n 个由空格隔开的正整数 a[i]。

输出格式

输出文件共有 T 行，对于每组数据，输出一行一个正整数，表示所有与 (n,a) 等价的货币系统 (m,b) 中，最小的 m。

代码：
#include <bits/stdc++.h>

using namespace std;

const int N=150;

int a[N];

int f[300000];

int n;

int t;

bool st[N];

int main(){

    scanf("%d",&t);

    while(t--){

        scanf("%d",&n);

        for(int i=1;i<=n;i++)scanf("%d",&a[i]);

        sort(a+1,a+1+n);

        memset(f,0,sizeof f);

        f[0]=1;

        int res=0;

        for(int i=1;i<=n;i++){

            if(f[a[i]])continue;

            res++;

            for(int j=a[i];j<=a[n];j++){

                f[j]=f[j]|f[j-a[i]];

            }

        }

        cout<<res<<endl;

    }

}

有依赖的背包问题

有 N个物品和一个容量是 V 的背包。

物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点。

如下图所示：

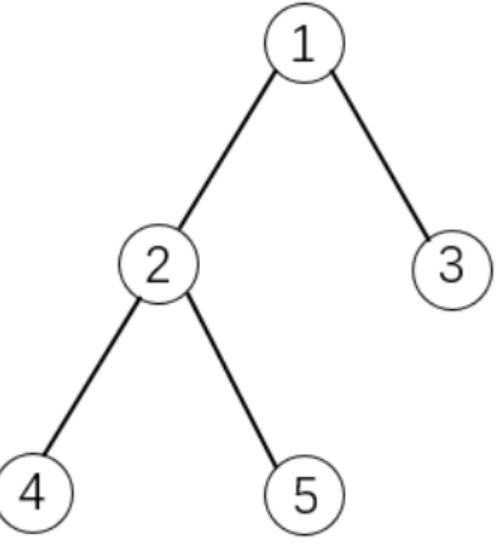
如果选择物品5，则必须选择物品1和2。这是因为2是5的父节点，1是2的父节点。

每件物品的编号是 ii，体积是 vivi，价值是 wiwi，依赖的父节点编号是 pipi。物品的下标范围是 1…N1…N。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

输入格式

第一行有两个整数 N，VN，V，用空格隔开，分别表示物品个数和背包容量。

接下来有 NN 行数据，每行数据表示一个物品。
第 ii 行有三个整数 vi,wi,pivi,wi,pi，用空格隔开，分别表示物品的体积、价值和依赖的物品编号。
如果 pi=−1pi=−1，表示根节点。 数据保证所有物品构成一棵树。

输出格式

输出一个整数，表示最大价值。

数据范围

1≤N,V≤1001≤N,V≤100
1≤vi,wi≤1001≤vi,wi≤100

父节点编号范围：

内部结点：1≤pi≤N1≤pi≤N;

根节点 pi=−1pi=−1

代码：

#include<bits/stdc++.h>

using namespace std;

const int N=110;

int f[N][N];

int v[N],w[N];

unordered_map<int,vector<int>>e;

int n,m;

void dfs(int u){

    for(int to:e[u]){

        dfs(to);

        for(int j=m;j>=w[u];j--){//循环 子树 使用体积,最少是w[u]

            for(int k=w[u];k<=j;k++)//循环 根 用的体积,最少是w[u]

                f[u][j]=max(f[u][j],f[u][k]+f[to][j-k]);//f[u][k]+f[to][j-k]

        }

    }

    

    for(int j=w[u];j<=m;j++)f[u][j]+=v[u];

    

}

int main(){

    scanf("%d%d",&n,&m);

    int root=0;

    for(int i=1;i<=n;i++){

        int a,b,c;

        scanf("%d%d%d",&b,&a,&c);

        v[i]=a;

        w[i]=b;

        if(c==-1)root=i;

        else e[c].push_back(i);

    }

    dfs(root);

    cout<<f[root][m];

}

状态压缩dp基础：

二进制枚举

#include<bits/stdc++.h>

using namespace std;

int n;

void op(int x){

    for(int i=0;i<n;i++){

        if((x>>i)&1){

            cout<<i+1<<' ';

        }

    }

    

}

int main(){

    scanf("%d",&n);

    for(int i=0;i<1<<n;i++){

        op(i);

        if(i+1!=1<<n)cout<<endl;

    }

}

棋盘型状态压缩dp

蒙德里安的梦想：

求把 N×MN×M 的棋盘分割成若干个 1×21×2 的长方形，有多少种方案。

例如当 N=2，M=4N=2，M=4 时，共有 55 种方案。当 N=2，M=3N=2，M=3 时，共有 33 种方案。

如下图所示：

输入格式

输入包含多组测试用例。

每组测试用例占一行，包含两个整数 NN 和 MM。

当输入用例 N=0，M=0N=0，M=0 时，表示输入终止，且该用例无需处理。

输出格式

每个测试用例输出一个结果，每个结果占一行。

#include <bits/stdc++.h>

using namespace std;

// 定义常量 N 表示棋盘的列数相关的一个上限值，M 表示所有可能的状态数（2 的 N 次方）

const int N = 12, M = 1 << N;  

// f 数组用于动态规划，第一维表示列数，第二维表示每一列的所有可能状态，存储方案数

long long f[N][M];  

// st 数组用于存储每种状态是否有奇数个连续的 0，若有奇数个连续 0 则该状态无效，否则为 true

bool st[M];  

// state 是一个二维数组（这里用 vector<vector<int>> 实现），用于记录每一种状态下合法的前一列状态

vector<vector<int>> state(M);  

int m, n;  // m 表示棋盘的列数，n 表示棋盘的行数

int main() {

    // 持续读入 n 和 m，只要 n 和 m 不同时为 0，就继续执行循环体

    while (cin >> n >> m, n || m) {

        // 遍历所有可能的状态（用二进制数表示，范围是 0 到 2 的 n 次方减 1）

        for (int i = 0; i < (1 << n); i++) {

            int cnt = 0;  // 用于记录连续的 0 的个数

            bool isValid = true;  // 标记某种状态是否没有奇数个连续的 0，初始设为 true

            // 遍历当前状态的每一位（对应棋盘的每一行），判断是否存在奇数个连续的 0

            for (int j = 0; j < n; j++) {

                // 判断状态 i 的二进制表示中第 j 位是否为 1

                if ((i >> j) & 1) {  

                    // 如果当前位为 1，检查前面连续的 0 的个数是否为奇数

                    if (cnt & 1) {

                        // 如果是奇数个连续的 0，则该状态不合法，标记为 false 并跳出循环

                        isValid = false;

                        break;

                    }

                    // 重置连续 0 的计数器，因为当前位为 1，新的连续 0 计数开始

                    cnt = 0;

                }

                else {

                    // 当前位为 0，连续 0 的计数器加 1

                    cnt++;

                }

            }

            // 检查最后一段连续的 0 的个数是否为奇数，如果是则状态不合法

            if (cnt & 1)  

                isValid = false;

            // 将状态 i 是否有奇数个连续 0 的情况记录到 st 数组中

            st[i] = isValid;

        }

        // 遍历第 i 列的所有状态（用二进制数表示，范围是 0 到 2 的 n 次方减 1）

        for (int j = 0; j < (1 << n); j++) {

            // 清空上一次操作遗留的状态，避免影响本次状态的判断

            state[j].clear();

            // 遍历第 i - 1 列的所有状态（用二进制数表示，范围是 0 到 2 的 n 次方减 1）

            for (int k = 0; k < (1 << n); k++) {

                // 判断第 i 列的状态 j 和第 i - 1 列的状态 k 是否没有冲突（按位与为 0）

                // 并且它们合并后的状态是合法的（st[j | k] 为 true）

                if ((j & k) == 0 && st[j | k])

                    // 如果满足条件，则将第 i - 1 列的状态 k 记录为第 i 列状态 j 的合法前一状态

                    state[j].push_back(k);  

            }

        }

        // 动态规划部分开始，初始化 f 数组为 0

        memset(f, 0, sizeof f);  

        // 初始化第 0 列，状态为 0 的方案数为 1

        f[0][0] = 1;

        // 遍历每一列（从第 1 列到第 m 列）

        for (int i = 1; i <= m; i++) {

            // 遍历当前列（第 i 列）的所有状态 j（用二进制数表示，范围是 0 到 2 的 n 次方减 1）

            for (int j = 0; j < (1 << n); j++) {  

                // 遍历第 i - 1 列中与当前状态 j 合法的所有状态 k

                for (auto k : state[j])  

                    // 当前列状态 j 的方案数等于上一列（第 i - 1 列）状态 k 的方案数之和

                    f[i][j] += f[i - 1][k];    

            }

        }

        // 输出第 m 列，状态为 0 的方案数

        cout << f[m][0] << endl;

    }

    return 0;

}

最短hamilton路径：

题目描述

给定一张 n 个点的带权无向图，点从 0∼n−1 标号，求起点 0 到终点 n−1 的最短 Hamilton 路径。

Hamilton 路径的定义是从 0 到 n−1 不重不漏地经过每个点恰好一次。

输入格式

第一行输入整数 n。

接下来 n 行每行 n 个整数，其中第 i 行第 j 个整数表示点 i−1 到 j−1 的距离（记为 a[i−1,j−1]）。

对于任意的 x,y,z，数据保证 a[x,x]=0，a[x,y]=a[y,x] 并且 a[x,y]+a[y,z]≥a[x,z]。

输出格式

输出一个整数，表示最短 Hamilton 路径的长度。

代码：
#include <bits/stdc++.h>

using namespace std;

const int N=21;

int g[N][N];

int f[1<<N][N];

int n;

int main(){

    cin>>n;

    for(int i=0;i<n;i++)

        for(int j=0;j<n;j++)

            cin>>g[i][j];

    memset(f,0x3f,sizeof f);

    f[1][0]=0;

    int m=1<<n;

    for(int i=0;i<m;i++){//遍历所有集合

        for(int j=0;j<n;j++){//从集合中的j

            if((1<<j)&i){//j在i中

                for(int k=0;k<n;k++){//走到k

                    if(k!=j&&(1<<k)&i){//j不等于k,并且k在i中

                        f[i][j]=min(f[i][j],f[i-(1<<j)][k]+g[k][j]);//从k转移过来

                    }

                }

            }

        }

    }

    cout<<f[m-1][n-1];

    return 0;

}

玉米田：

农夫约翰的土地由 M×NM×N 个小方格组成，现在他要在土地里种植玉米。

非常遗憾，部分土地是不育的，无法种植。

而且，相邻的土地不能同时种植玉米，也就是说种植玉米的所有方格之间都不会有公共边缘。

现在给定土地的大小，请你求出共有多少种种植方法。

土地上什么都不种也算一种方法。

输入格式

第 11 行包含两个整数 MM 和 NN。

第 2..M+12..M+1 行：每行包含 NN 个整数 00 或 11，用来描述整个土地的状况，11 表示该块土地肥沃，00 表示该块土地不育。

输出格式

输出总种植方法对 108108 取模后的值。

代码：
#include<bits/stdc++.h>

using namespace std;

const int mod=1e9;

const int N=15;

int f[N][1<<N];

int n,m;

vector<int> t;

unordered_map<int,vector<int>> e;

int g[N];

int op(int x){

    return ((x+mod)%mod+mod)%mod;

}

bool check(int x){//连续的两个不能都是1

    if(x&(x<<1))return false;

    return true;

}

int main(){

    cin>>n>>m;

    for(int i=0;i<(1<<m);i++){

        if(check(i))t.push_back(i);

    }

    for(int i:t){

        for(int j:t){//和j匹配的i

            if((i&j)==0)e[i].push_back(j);

        }

    }

    

    for(int i=1;i<=n;i++){

        for(int j=0;j<m;j++){

            int tmp;

            cin>>tmp;

            if(tmp==0){

                g[i]+=(1<<j);

            }

        }

    }//读入状态

    

    f[0][0]=1;

    for(int i=1;i<=n+1;i++){

        for(int j:t){

            if(j&g[i])continue;//没有种在坏地上

            for(int k:e[j]){

                if(k&g[i-1])continue;//上一行也合法

                f[i][j]=op(f[i][j]+f[i-1][k]);

            }

        }

    }

    cout<<f[n+1][0];

}

炮兵阵地：

题目描述

司令部的将军们打算在 N×M 的网格地图上部署他们的炮兵部队。

一个 N×M 的地图由 N 行 M 列组成，地图的每一格可能是山地（用 H 表示），也可能是平原（用 P 表示），如下图。

在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。

图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。

现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

输入格式

第一行包含两个由空格分割开的正整数，分别表示 N 和 M。

接下来的 N 行，每一行含有连续的 M 个字符，按顺序表示地图中每一行的数据。

输出格式

一行一个整数，表示最多能摆放的炮兵部队的数量。

代码：
#include <bits/stdc++.h>

using namespace std;

const int N=110,M=(1<<10);

int s[N]={0},cnt[M];

int n,m;

int state[M];

int f[2][M][M]={0};

bool check (int st){

    for(int i=0;i<10;i++){

        if(((st>>i)&1)&&(((st>>(i+1))&1)||((st>>(i+2))&1)))//3个连续的地方只有1个1

            return false;

    }

    return true;

}

int count(int st){

    int res=0;

    for(int i=0;i<11;i++){

        if((st>>i)&1)res++;

    }

    return res;

}

int main(){

    cin>>n>>m;

    for(int i=1;i<=n;i++){

        for(int j=0;j<m;j++){

            char tmp;

            cin>>tmp;

            if(tmp=='H')

                s[i]+=(1<<j);

        }

    }

    

    int cn=0;

    int t=1<<m;

    

    for(int i=0;i<t;i++){//遍历所有的状态

        if(check(i)){//i状态合法

            state[cn++]=i;//将其加入到state种

            cnt[i]=count(i);//同时计算状态中的炮兵数量

        }

    }

    

    for(int i=1;i<=n+2;i++)//遍历到n+2,最后的答案是n+2行的状态是0

        for(int j=0;j<cn;j++)//第i-1行的状态

            for(int k=0;k<cn;k++)//第i行的状态

                for(int u=0;u<cn;u++){//i-2行的状态

                    int a=state[k],b=state[j],c=state[u];

                    

                    if((a&c)||(b&c)||(a&b))continue;//3行里面不能有炮兵重叠

                    if(s[i]&a||s[i-1]&b)continue;//山地冲突

                    if(i>=2&&s[i-2]&c)continue;//山地冲突

                    f[i&1][j][k]=max(f[i&1][j][k],f[i-1&1][u][j]+cnt[a]);

                }

    cout<<f[n+2&1][0][0];//state[0]对应状态0000000000

}

愤怒的小鸟：

题目背景

NOIP2016 提高组 D2T3

题目描述

Kiana 最近沉迷于一款神奇的游戏无法自拔。

简单来说，这款游戏是在一个平面上进行的。

有一架弹弓位于 (0,0) 处，每次 Kiana 可以用它向第一象限发射一只红色的小鸟，小鸟们的飞行轨迹均为形如 y=ax2+bx 的曲线，其中 a,b 是 Kiana 指定的参数，且必须满足 a<0，a,b 都是实数。

当小鸟落回地面（即 x 轴）时，它就会瞬间消失。

在游戏的某个关卡里，平面的第一象限中有 n 只绿色的小猪，其中第 i 只小猪所在的坐标为 (xi​,yi​)。

如果某只小鸟的飞行轨迹经过了 (xi​,yi​)，那么第 i 只小猪就会被消灭掉，同时小鸟将会沿着原先的轨迹继续飞行；

如果一只小鸟的飞行轨迹没有经过 (xi​,yi​)，那么这只小鸟飞行的全过程就不会对第 i 只小猪产生任何影响。

例如，若两只小猪分别位于 (1,3) 和 (3,3)，Kiana 可以选择发射一只飞行轨迹为 y=−x2+4x 的小鸟，这样两只小猪就会被这只小鸟一起消灭。

而这个游戏的目的，就是通过发射小鸟消灭所有的小猪。

这款神奇游戏的每个关卡对 Kiana 来说都很难，所以 Kiana 还输入了一些神秘的指令，使得自己能更轻松地完成这个游戏。这些指令将在【输入格式】中详述。

假设这款游戏一共有 T 个关卡，现在 Kiana 想知道，对于每一个关卡，至少需要发射多少只小鸟才能消灭所有的小猪。由于她不会算，所以希望由你告诉她。

输入格式

第一行包含一个正整数 T，表示游戏的关卡总数。

下面依次输入这 T 个关卡的信息。每个关卡第一行包含两个非负整数 n,m，分别表示该关卡中的小猪数量和 Kiana 输入的神秘指令类型。接下来的 n 行中，第 i 行包含两个正实数 xi​,yi​，表示第 i 只小猪坐标为 (xi​,yi​)。数据保证同一个关卡中不存在两只坐标完全相同的小猪。

如果 m=0，表示 Kiana 输入了一个没有任何作用的指令。

如果 m=1，则这个关卡将会满足：至多用 ⌈n/3+1⌉ 只小鸟即可消灭所有小猪。

如果 m=2，则这个关卡将会满足：一定存在一种最优解，其中有一只小鸟消灭了至少 ⌊n/3⌋ 只小猪。

保证 1≤n≤18，0≤m≤2，0<xi​,yi​<10，输入中的实数均保留到小数点后两位。

上文中，符号 ⌈c⌉ 和 ⌊c⌋ 分别表示对 c 向上取整和向下取整，例如：⌈2.1⌉=⌈2.9⌉=⌈3.0⌉=⌊3.0⌋=⌊3.1⌋=⌊3.9⌋=3。

输出格式

对每个关卡依次输出一行答案。

输出的每一行包含一个正整数，表示相应的关卡中，消灭所有小猪最少需要的小鸟数量。

代码：

#include<bits/stdc++.h>

using namespace std;

typedef pair<double,double> pdd;

const int N=20;

bool same(double x,double y){

    if(fabs(x-y)<1e-6)return 1;

    return 0;

}

int t,n,m;

pdd a[N];

int f[N][N];

int g[1<<N];

int main(){

    scanf("%d",&t);

    while(t--){

        cin>>n>>m;

        for(int i=0;i<n;i++){

            cin>>a[i].first>>a[i].second;

        }

        memset(f,0,sizeof f);

        

        for(int i=0;i<n;i++){

            f[i][i]=1<<i;

            

            for(int j=0;j<n;j++){

                if(i==j)continue;

                

                double x1=a[i].first,y1=a[i].second;

                double x2=a[j].first,y2=a[j].second;

                if(same(x1,x2))continue;

                

                double aa=(y1/x1-y2/x2)/(x1-x2);

                if(aa>0)continue;

                double bb=y1/x1-aa*x1;

                int st=0;

                for(int k=0;k<n;k++){

                    double x=a[k].first,y=a[k].second;

                    if(same(aa*x*x+bb*x,y)){

                        st+=1<<k;

                    }

                }

                f[i][j]=st;//表示从依据i和j建立的抛物线覆盖的点集合

            }

        }

    

        memset(g,0x3f,sizeof g);

        g[0]=0;

        for(int i=0;i<1<<n;i++){

            int x=0;

            for(int j=0;j<n;j++){//找到没有被覆盖的点

                if(i>>j&1){

                    continue;

                }else {

                    x=j;

                    break;

                }

            }

            for(int j=0;j<n;j++){

                g[i|f[x][j]]=min(g[i|f[x][j]],g[i]+1);

            }

        }

        cout<<g[(1<<n)-1]<<endl;

        

    }

    

}

明天从区间Dp开始看