当前位置：首页 > news >正文

【C++】数据结构九种排序算法的实现

news 来源：原创 2025/7/5 2:29:41

本篇博客给大家带来的是直接插入、希尔、直接选择、堆、冒泡、快速、归并、计数、排序算法的实现！

🐟🐟文章专栏：数据结构

🚀🚀若有问题评论区下讨论，我会及时回答

❤❤欢迎大家点赞、收藏、分享！

今日思想：疯狂的不是我，是整个世界！

一、常见排序算法

二、插入排序

插入排序：把待排序的值按大小一个个插入到有序的序列中，例如：玩扑克牌。

1、直接插入排序

我们看一下这个数组，这是一个降序的数组，我们让它变成升序。

步骤：

一开始我们定义两个值（end和tmp）: end = 0，tmp= arr [ end+1 ]，然后进行比较（如果arr[end]>tmp，就arr[end+1] = arr[ end ]，然后end--，这时候end= - 1，end<0，再把arr[ end+1 ] = tmp）。

接下来end来到下标为1的值那里，tmp保存下标为2的值，然后再比较（比较方法和上面一样）。

重复上面的步骤之后：

思想风暴：

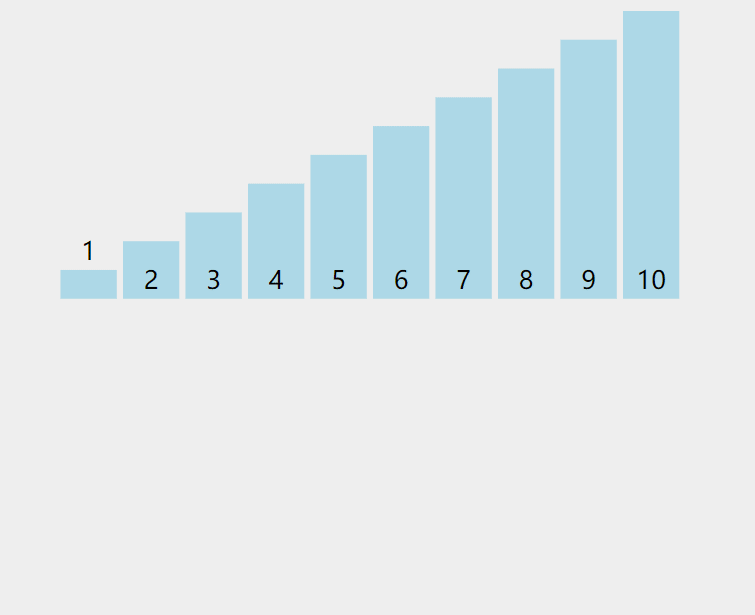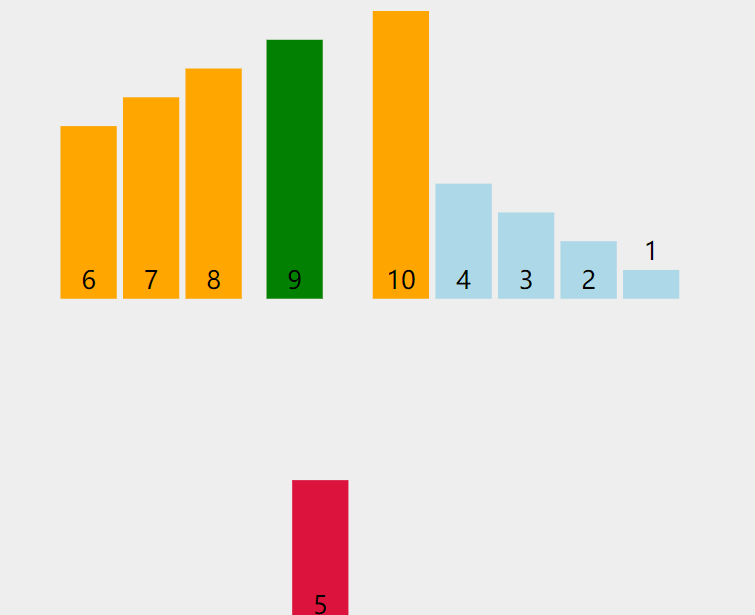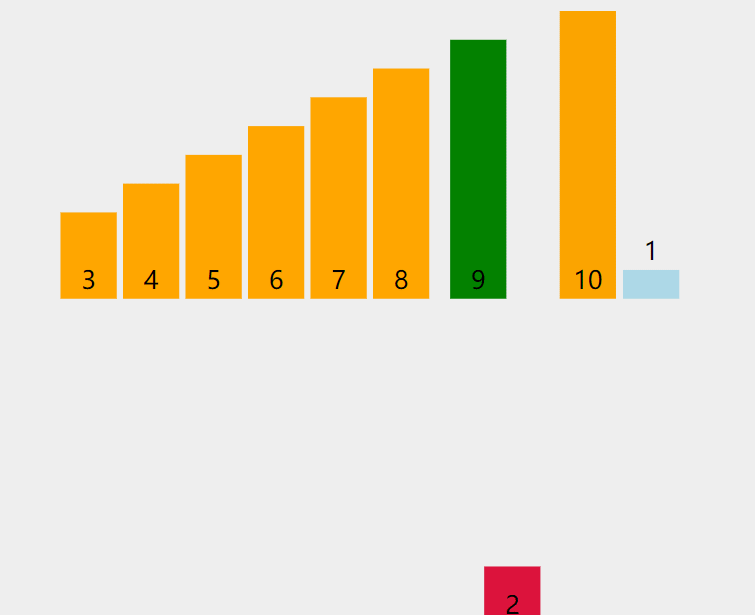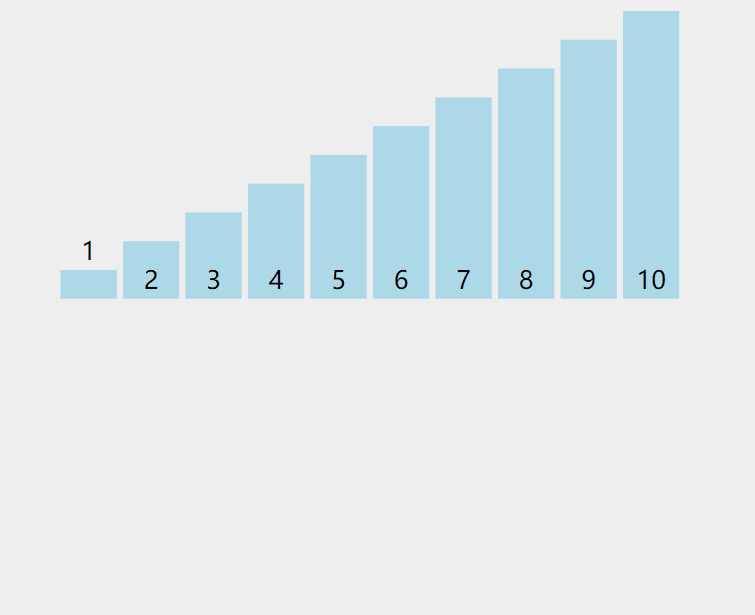
代码实例：

//直接插入排序
void InserSort(int* arr, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = arr[end + 1];while (end >= 0){if (arr[end] > tmp){arr[end + 1] = arr[end];end--;}else{break;}}arr[end + 1] = tmp;}
}

时间复杂度：
最差情况：O(n^2)数组为降序，当大部分大的值放到数组前面，大部分小的值放到数组的后面，时间复杂度近似最差情况。

最好情况：O(n)数组为升序，当大部分的值放到数组的后面，大部分小的值放到数组的前面，时间复杂度近似最好情况。

空间复杂度：O(1)

2、希尔排序

希尔排序是在直接插入排序的基础上优化的，通过一系列的分组把大部分大的数据放到数组的后面来降低时间复杂度。

步骤：

注意：上面有10个数字，一开始gap=10，gap=gap/3+1之后gap=4，由于一些原因这里的gap=5，但是不影响讲解。gap是组数和两个数字之间的距离例如9到4的距离是5。上面排序完之后的数据不是最终有序数据而是当gap=5时排序完之后的数据。

首先：进行分组之后，我们进行排序，这里的排序跟直接插入排序差不多，我们让end=0,tmp=arr[end+gap],然后就是比较大小，end-=gap，之后arr[end+gap]=tmp;

接着end++

经过一系列end++之后

排序完之后gap=gap/3+1,再接着完成上面的步骤，最终为：

只要gap>1，就继续分组排序。

注意：当gap=1时并没有判断gap>1,gap=1是在gap=2判断结束之后gap=1,所以还会继续执行排序。当gap=1时跟直接插入排序没什么区别了，不过大部分大的数据放到数组的后面了，大大降低了时间复杂度。

代码实例：

//希尔排序
void ShellSort(int* arr, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){int end = i;int tmp = arr[end + gap];while (end >= 0){if (arr[end] > tmp){arr[end + gap] = arr[end];end -= gap;}else{break;}}arr[end + gap] = tmp;}}
}

希尔排序时间复杂度：O（n^1.3）

推演：

外层循环时间复杂度：我们可以直接给出外层时间复杂度为：O（log2^n）或者O（log3^n），即O（logn）。原因：外层循环就是上面while循环，他的时间复杂度看gap/2还是gap/3.

内层循环：假设n=9，若gap=3，则一共gap组，每组n/gap个数据。

根据上面的图我们来分析一下第一组数据移动的次数：第一组3个数据，次数移动=1+2=3。

假设有n个数据，一共gap组每组n/gap个数据

因为一共有gap组，所以总的移动次数：gap*[1+2+3.....(n/gap-1)]

注意：上面的公式是由上面的1+2=3推来的，2是每组的数据个数-1的来的，所以n/gap-1。

gap取值：n/3，n/9，n/27.....1

注意：一开始gap=n，所以gap和n没啥区别，这里不用gap/3+1，因为+1是一个非常小的值，在时间复杂度里面不算什么。

当gap为n/3时，移动总数为：n/3*(1+2)=n

注意：套用上面的公式：gap*[1+2+3+....+(n/gap-1)]

当gap/9时，移动总数为：n/9*[1+2+3+....+8]=(n/9)*([8(1+8)]/2)=4n

注意：([8(1+8)]/2)这个是由等差求和公式得来的

。。。。。

最后gap肯定得1，这时候就是直接插入排序，当然这时候大的数据大部分放到数组的后面，所以移动总是近似为：n

总结：移动总数一开始慢慢变大，达到顶点之后慢慢变小近似n，没有达到n。

注意：顶点我们目前无法求取，为什么呢，因为涉及一些目前数学上未解决的问题。

我们只要知道根据《数据结构（C语言版）》——严蔚敏给出的希尔排序的时间复杂度为O（n^1.3）就行。

三、选择排序

基本思想：每一次从待排序的数据元素中选出一个最小或者最大的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

图解：

1、直接选择排序

直接选择是定义begin和end两个变量，begin起始位置在数组下标为0的数字，end的起始位置在最后一个数字那里，我们又定义两个变量maxi和mini，他们的起始位置都在下标为0那里，再定义一个变量 i 一开始i=begin，它遍历数组的数据只要 i > maxi 那么maxi = i，如果 i < mini，那么minx=i，最后 maxi 和 end 交换位置，mini 和 begin 交换位置，begin++，end-- 。重复以上的操作得到最后的升序序列。

注意：i 遍历数组的范围 [ begin , end ]

思想风暴：

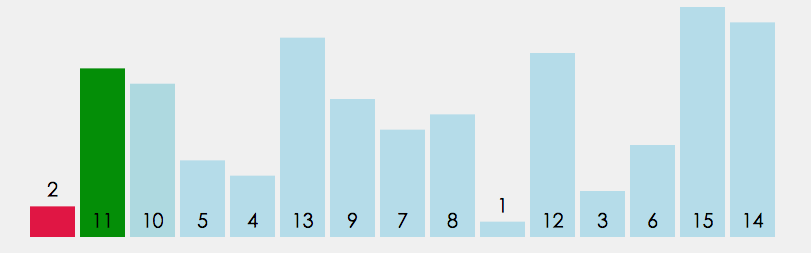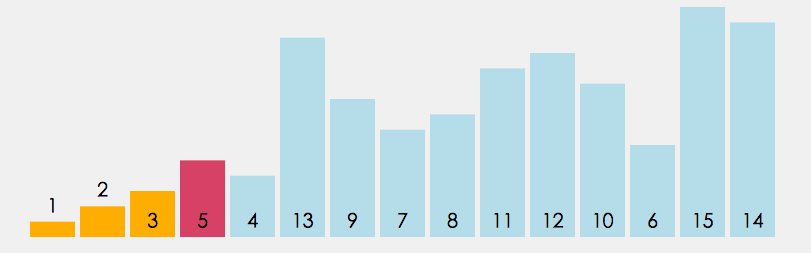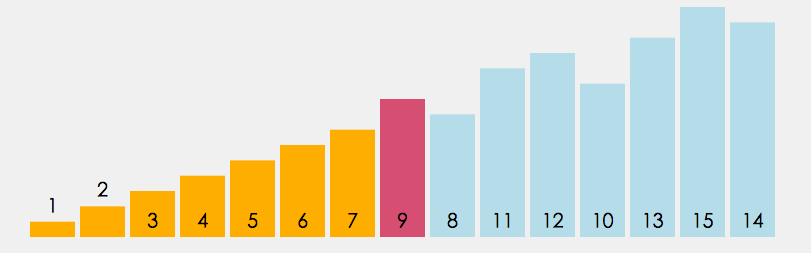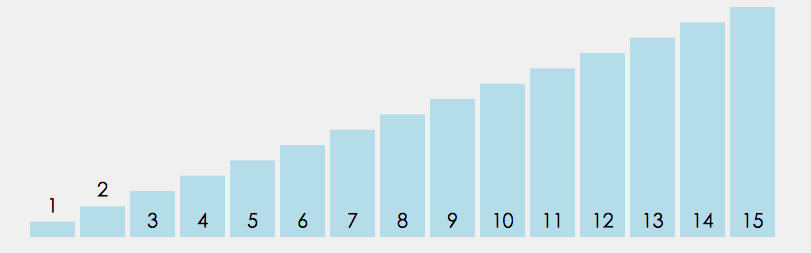
图解：

关于上面细节的解释：

代码实例：

void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}
//直接选择排序
void SelectSort(int* arr, int n)
{int begin = 0, end = n - 1;while (begin < end){int mini = begin, maxi = begin;for (int i = begin; i <= end; i++){if (arr[i] > arr[maxi]){maxi = i;}else if (arr[i] < arr[mini]){mini = i;}}if (maxi == begin){maxi = mini;}Swap(&arr[begin], &arr[mini]);Swap(&arr[end], &arr[maxi]);begin++;end--;}
}

时间复杂度：O（n^2）

2、堆排序

关于堆排序之前我的一篇博客说过，这里就不再细讲了，具体内容请看博客：

【C++】树和二叉树的实现（上）-CSDN博客

【C++】树和二叉树的实现（下）-CSDN博客

注意：第一个博客是为第二个博客做铺垫，堆排序就是第二个博客内容的建大堆和小堆。

四、交换排序

关键：大的值向序列的尾部移动，小的往前面移动。

1、冒泡排序

通过一个个值的比较，达到最佳位置。

图解：

思想风暴：

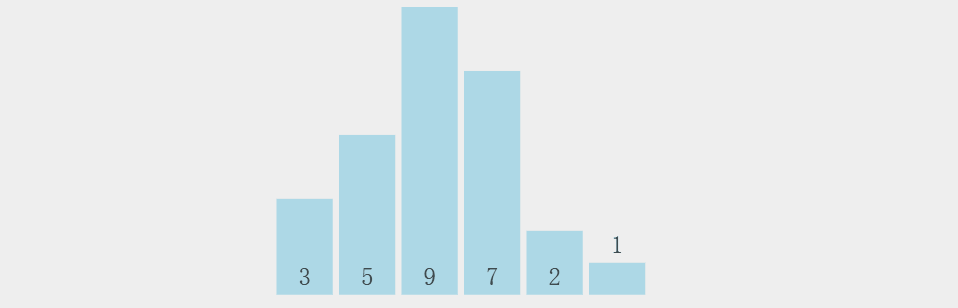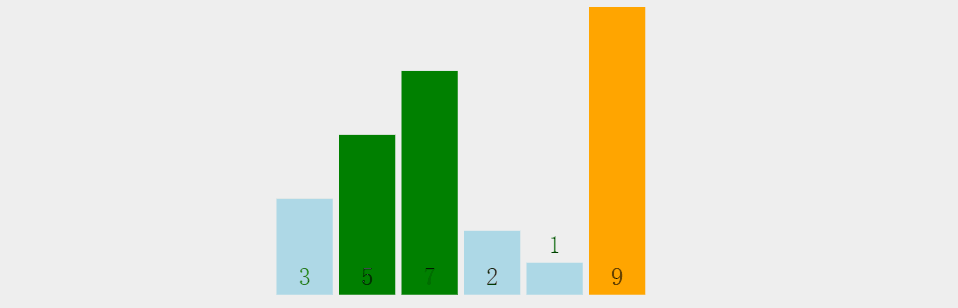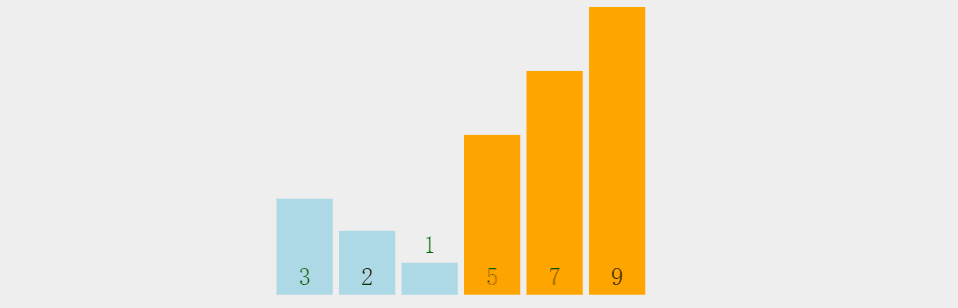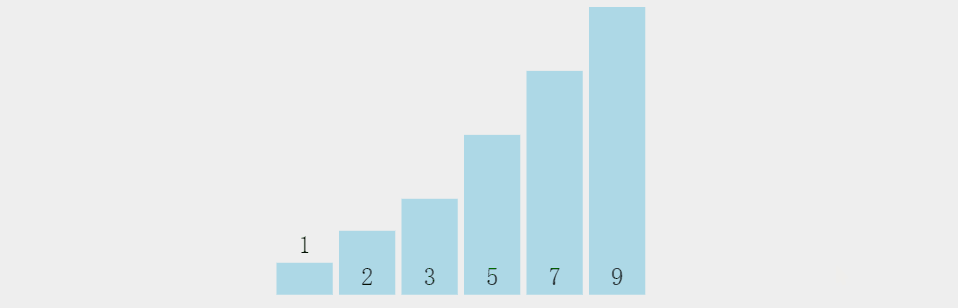时间复杂度：O（n^2）

空间复杂度：O（1）

代码实例：


void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}//冒泡排序
void BubbleSort(int* arr, int n)
{int k = 0;//标记，如果经过一系列的交换k还是等于0，表示这个数组的有序的for (int i = 0; i < n; i++){for (int j = 0; j < n - 1; j++){if (arr[j] > arr[j + 1]){Swap(&arr[j], &arr[j + 1]);k = 1;}}if (k == 0){break;}}
}

2、快速排序

2.1递归版本

快速排序是Hoare在1962年提出的一种二叉树结果的交换排序方法，其实就是递归。思想：通过寻找序列的基准值，然后将待排序分成两部分序列，然后将这两个序列排序，再将这两个序列再分，重复分，最后得到有序序列。

图解：

思想风暴：

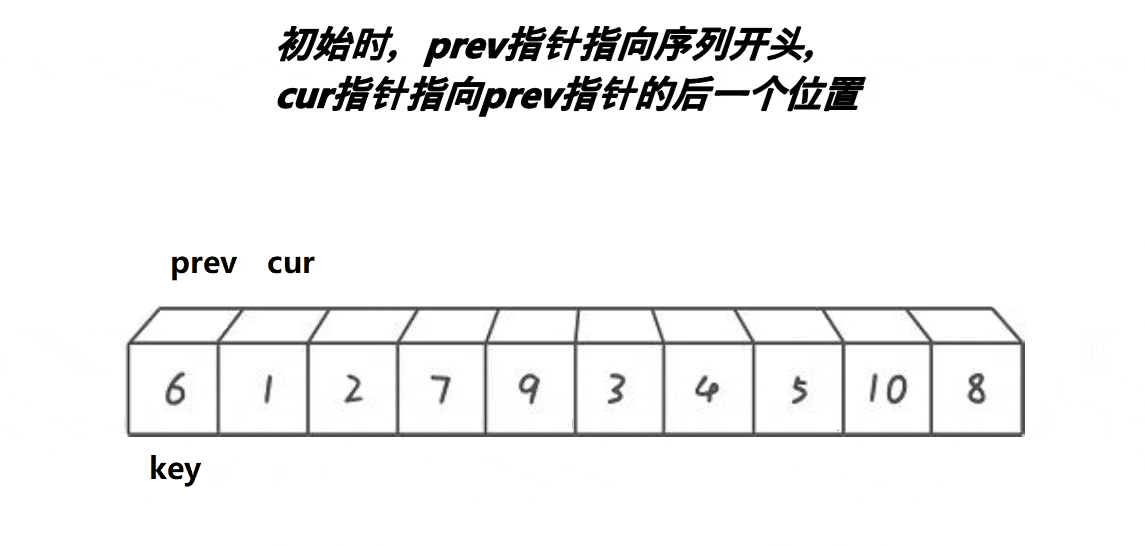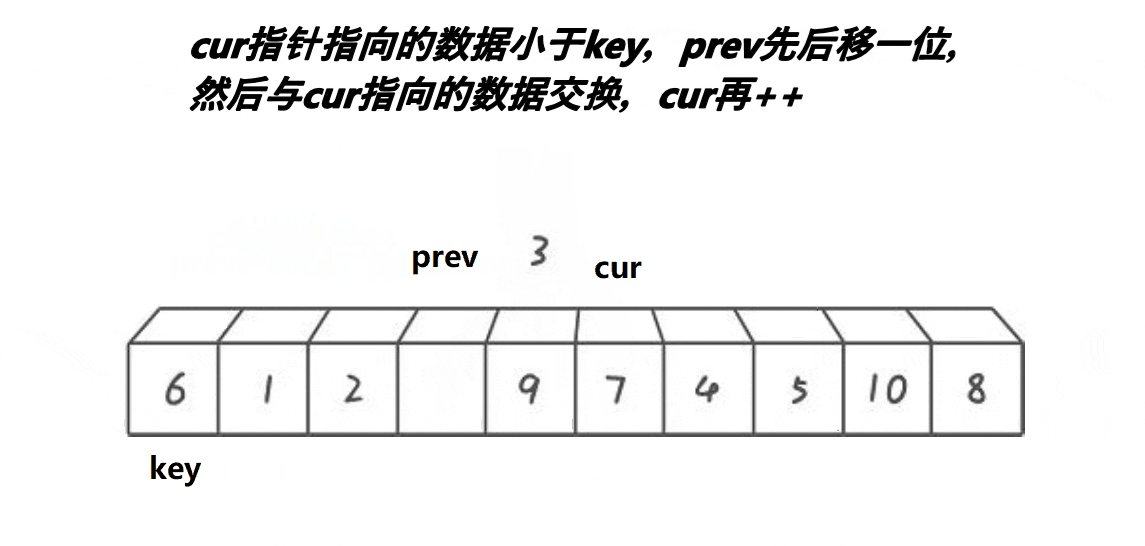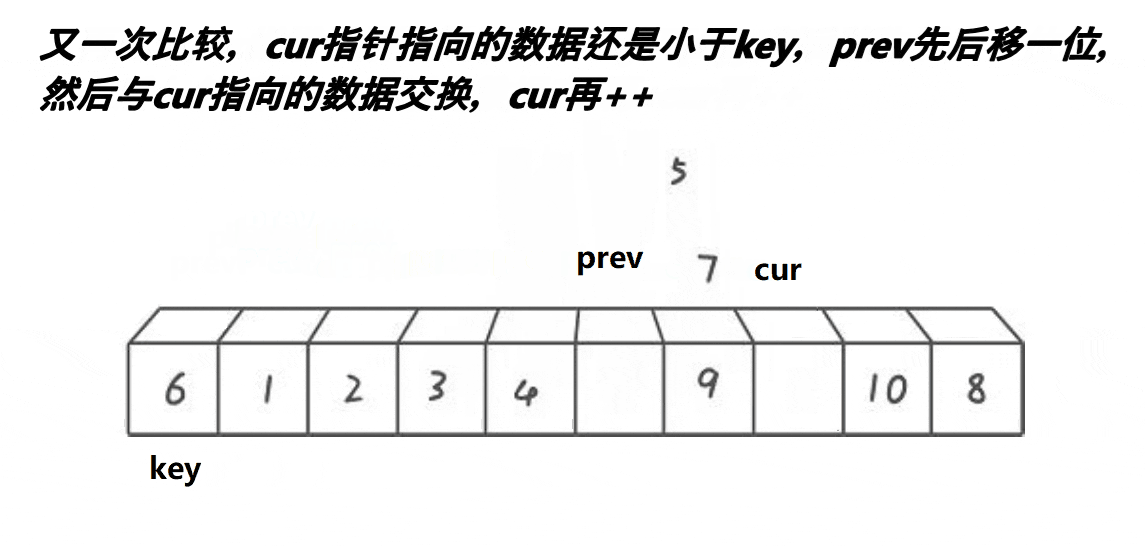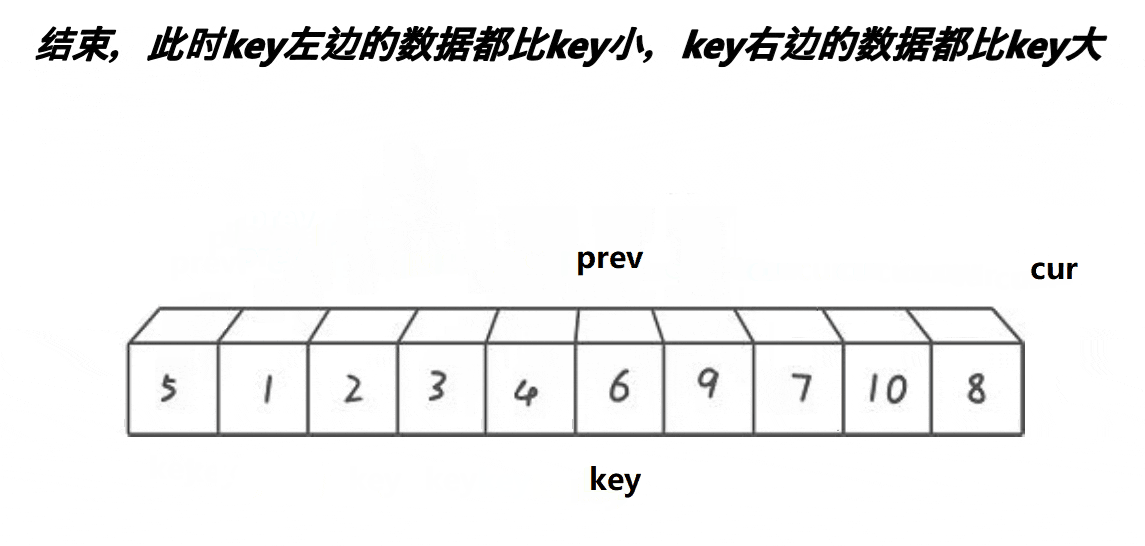
代码实例：

void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}
int _QuickSort(int* arr, int left, int right)
{int keyi = left;left++;while (left <= right){while (left <= right && arr[right] > arr[keyi]){right--;}while (left <= right && arr[left] < arr[keyi]){left++;}if (left <= right){Swap(&arr[left++], &arr[right--]);}}Swap(&arr[keyi], &arr[right]);return right;
}
}
//快速排序
void QuickSort(int* arr, int left, int right)
{if (left >= right){return;}//找基准值int keyi = _QuickSort(arr, left, right);//左序列[left,keyi-1]	右序列：[keyi+1,right]QuickSort(arr, left, keyi - 1);QuickSort(arr, keyi+1,right);
}

时间复杂度：O（nlogn）

注意：如果基准值找的不好或者序列有序，时间复杂度为O（n^2）。例如：

那么这里有个更好找基准值的办法：

lomuto前后指针找基准值法：

创建三个变量（keyi，cur，prev），keyi指向第一个数据，prev一开始指向第一个数据，cur指向prev+1。cur在前面找比keyi指向的值小的数据，找到：prev++，arr[ prev ]和arr[ cur ]交换（注意当当 prev = cur 时不能交换）之后 cur++，找不到：cur++。当cur越过数组下标的最大值时交换arr[ prev ]和arrp[ keyi ]并且返回 prev ，此时 prev 就是基准值。

图解：

代码实例：

int _QuickSort2(int* arr, int left, int right)
{int keyi = left;int prev = left, cur = prev + 1;while (cur <= right){if (arr[cur] < arr[keyi] && ++prev != cur){Swap(&arr[prev], &arr[cur]);}cur++;}Swap(&arr[prev], &arr[keyi]);return prev;
}
//快速排序
void QuickSort(int* arr, int left, int right)
{if (left >= right){return;}//找基准值int keyi = _QuickSort2(arr, left, right);//左序列[left,keyi-1]	右序列：[keyi+1,right]QuickSort(arr, left, keyi - 1);QuickSort(arr, keyi+1,right);
}

2.2非递归版本

我们上面利用了递归来实现对数组不断的裂开进而通过找基准值来排序，那么不用递归我们怎么实现裂开数组然后对数组找基准值来排序呢？答案是：我们通过栈来实现，把数组的下标入栈栈，不断的出栈和入栈来实现递归的裂开。

注意：如果大家对栈有点遗忘可以看一下我写的博客：

【C++】数据结构栈的实现_c++ 栈实例-CSDN博客

图解：

代码实例：

int _QuickSort2(int* arr, int left, int right)
{int keyi = left;int prev = left, cur = prev + 1;while (cur <= right){if (arr[cur] < arr[keyi] && ++prev != cur){Swap(&arr[prev], &arr[cur]);}cur++;}Swap(&arr[prev], &arr[keyi]);return prev;
}
//非递归版本的快速排序
void QuickSortNonR(int* arr, int left, int right)
{ST st;STInit(&st);StackPush(&st, right);StackPush(&st, left);while (!StackEmpty(&st)){//取两次栈顶int begin = StackTop(&st);StackPop(&st);int end = StackTop(&st);StackPop(&st);//找基准值int keyi = _QuickSort2(arr, begin, end);//左序列：【begin,keyi-1】右序列：【keyi+1,end】if (keyi + 1 < end){StackPush(&st, end);StackPush(&st, keyi + 1);}if (begin < keyi - 1){StackPush(&st, keyi - 1);StackPush(&st, begin);}}STDestroy(&st);
}

五、归并排序

归并排序就是把一个数组不断的分成两个数组，最终分成单个数据，让后不断的两两比较把单个数据合并。

图解：

代码实例：

void _MergeSort(int* arr, int left, int right, int* tmp)
{//分解if (left >= right){return;}int mid = (left + right) / 2;//划分左右两个序列：【left，mid】【mid+1,right】_MergeSort(arr, left, mid, tmp);_MergeSort(arr, mid + 1, right, tmp);//合并两个序列：[left,mid] [mid+1,right]int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;int index = begin1;while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] < arr[begin2]){tmp[index++] = arr[begin1++];}else{tmp[index++] = arr[begin2++];}}//右序列的数据没有完全放到tmp数组中//左序列的数据没有完全放到tmp数组中while (begin1 <= end1){tmp[index++] = arr[begin1++];}while (begin2 <= end2){tmp[index++] = arr[begin2++];}//把数据放回到原来的数组中for (int i = left; i <= right; i++){arr[i] = tmp[i];}
}
//归并排序
void MergeSort(int* arr, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);_MergeSort(arr, 0, n - 1, tmp);free(tmp);
}

时间复杂度：O(n^logn)

六、总结

运行时间：堆排序 < 快速排序 < 希尔排序 < 归并排序 < 直接插入排序 < 直接选择排序 < 冒泡排序。

建议使用前四种排序方法。

七、附加算法（计数排序）

计数排序又称鸽巢原理，是对哈希直接定址法的变形应用。

规则：统计相同数据出现的次数，把次数放到数组里面进而排序。

图解：

注意：如果序列的值相差的值太大就不能用计数排序。例如：1，4，5，6，10000，10。申请空间范围range=10000-1=9999，造成空间浪费。

代码实例：

//非比较排序——计数排序
void CountSort(int* arr, int n)
{int min = arr[0], max = arr[0];//默认最大值和最小值都是arr[0]for (int i = 1; i < n - 1; i++)//找最大值和最小值{if (arr[i] < min){min = arr[i];}if (arr[i] > max){max = arr[i];}}int range = max - min + 1;int* count = (int*)malloc(sizeof(int) * range);if (count == NULL){perror("malloc fail!");}memset(count, 0, sizeof(int) * range);for (int i = 0; i < n; i++){count[arr[i] - min]++;}//把数据回原来的数组int index = 0;for (int i = 0; i < range; i++){while(count[i]--){arr[index++] = i + min;}}
}

时间复杂度:O（n*range）

八、稳定性

稳定性就是一个数组的任意两个数据经过排序之后前后顺序不变。

例如：a，n，b，c，d，e，f经过排序之后a还在b的前面。

目前来说以上这么多的排序算法只有冒泡排序、归并排序、直接插入排序稳定其他都不稳定。

完！！！！

一、常见排序算法

二、插入排序

1、直接插入排序

2、希尔排序

三、选择排序

1、直接选择排序

2、堆排序

四、交换排序

1、冒泡排序

2、快速排序

2.1递归版本

2.2非递归版本

五、归并排序

六、总结

七、附加算法（计数排序）

八、稳定性

相关文章：