当前位置： 首页 > news >正文

STM32江科大----------PID算法

news 来源：原创 2025/8/25 14:21:40

声明：本人跟随b站江科大学习，本文章是观看完视频后的一些个人总结和经验分享，也同时为了方便日后的复习，如果有错误请各位大佬指出，如果对你有帮助可以点个赞小小鼓励一下，本文章建议配合原视频使用❤️

如果你也正在学习STM32可以订阅本专栏，后续将不定期更新( ˘ ³˘)❤️
如有侵权，请私信联系删除
在这里插入图片描述

文章目录

  • 前言
  • 理论部分
    • 1.PID基本原理
      • PID简介
      • 开环与闭环
    • 2.PID算法原理
      • 比列项
      • 积分项
      • 微分项
    • 3.离散PID&程序实现思路
      • 连续和离散形式PID
      • 位置式PID和增量式PID
      • PID程序实现
    • 4.常见优化算法方法
      • 积分限幅（只用于位置式）
      • 积分分离（定位置）
      • 变速积分
      • 微分先行
      • 不完全微分
      • 输出偏移
      • 输入死区
      • 注意事项
    • 5.双环PID基本原理
      • 串级PID简介
      • 单双环对比
    • 6.调参技巧
  • 代码部分

前言

  • 这一块的学习还是得有实践，不亲自感受一下pid调参那么无异于没学
  • 想要制作平衡车的小伙伴建议再去学习一下姿态解算也是很有趣的
  • 了解PID每一项的作用以及计算方式很重要
  • 优化算法一定要根据实际情况来，不然容易起到反效果
  • 串级PID的优点和建立方法要理解
  • 调参要懂取舍，多调参才能积累经验

理论部分

1.PID基本原理

PID简介

在这里插入图片描述

  • 做小车就会用到PID算法，因为小车想要走直线就要保证两个轮子PWM输出的占空比一致，不一致小车就会走不直，可是你若只考虑输出相同的占空比，但是还会存在润滑油多少等外力因素，导致两个轮子速度肯定不一样，这时候为了保证速度相同就要使用PID算法

开环与闭环

在这里插入图片描述

  • 闭环相较于开环相当于多了一个反馈电路形成闭合环路，可根据反馈不断调节输出值来接近目标值，开环不会自己调节，输出一个值后就定死了，哪怕被控对象受外部因素而偏离目标值，输出值仍然不会自我调整

2.PID算法原理

在这里插入图片描述

  • 看这个图就知道PID是一种基于误差调控的算法，PID的目的是让误差为0
  • 第二个输出值公式更为常用，因为分别调节三个参数可以改变三项的值，便于调参，Kp,Ki,Kd是每一项的权重

比列项

在这里插入图片描述

  • Kp*error(t)就是系统调控的力度，假如error(t)=10，单位可能是速度转速等等，那么Kp给0.1的话，调控力度就是1，给1的话力度就是10，依次类推，所以Kp不能太大了，否则误差只要变化很小，比列这一项就会猛的一调，也就是超调，太小的话也不行系统响应会很慢
  • 但是不能只有比列这一项用于调节输出值，会存在稳态误差
    在这里插入图片描述
  • 红色线条表示电机目标速度，紫色线条是电机实际速度
  • 红色框框表示超调，蓝色差值表示稳态误差，稳定后的实际速度与目标速度的差值
  • 这个图就是只看P比例项的波形图，可以看到Kp越大红色框框的超调就越大
  • 按理来说只要存在误差P就会一直进行调节，那为什么会有稳态误差呢？先看看下面对稳态误差的介绍

稳态误差
在这里插入图片描述

  • 在理想情况时不存在稳态误差，但是由于电机旋转必然存在摩擦力，PID最终目的是误差为0，但是误差为0时我们的P项输出也为0，PID的输出结果直接送到了PWM的输出函数，也就是PWM输出为0了，电机也就没有驱动力不在转动，由于摩擦力肯定会减速，一旦减速就会有误差，PID又要开始加速，也就是PWM输出又会增加，驱动力也会增加，直到驱动力等于摩擦力时系统达到稳态
  • 可能有人会问当驱动力和摩擦力达到平衡时，稳态的值还没达到目标值，难道系统系统看不到吗，不会继续增大PWM吗？但是由于P项过后误差已经很小了，算法得出的结论是我提供这么多驱动力就够了，但是系统不知道有摩擦力这么个东西，导致提供的驱动力一直达不到目标值，也没人告诉他驱动力已经和摩擦力平衡了需要继续增大驱动力，所以才需要其他项来帮助PID算法
  • 积分项就是用于帮助消除稳态误差的，因为比列项输出值仅取决于当前误差，与历史时刻误差无关，这意味你想实现使用当前误差产生的占空比，并在此基础上加上比例项的输出作为新的占空比（这样误差为正必然加大占空比加速，为负必然减小占空比减速）是行不通的，或者说这其实是积分项的任务

积分项

在这里插入图片描述

  • 积分项用于消除稳态误差，也就是提醒系统你的驱动力用来平衡摩擦力了，还得更努力增大驱动力才能达到目标值
  • 写积分项程序要单独定义一个变量存储历史误差，误差不断累计并求和然后乘以一个积分系数得到积分项的输出
  • 积分项不断累积使其控制力度越来越大，直到能够让电机占空比变大，最终达到目标值消除稳态误差
  • 积分项的弊端就是系统滞后性：也就是当系统稳态误差消除后，此时突然要求电机反转，那么先要不断反向积分来消除正向的驱动力，然后再继续累计使其反转
  • 比列项相对于积分项来说变化非常快，因为只用考虑当前时刻，你说正就是正，你说负就是负，系统响应很快

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

微分项

在这里插入图片描述

  • 微分项不会消除误差
  • 主要作用是防止超调，阻止变化过快，提前调控
  • 打个比方，平衡车如果只有PI项很难稳定立起来，因为倒下太快了，PI来不及做出调整让重新平衡，D项的作用就是让他到下更慢一点，这是PI有更多时间调整
  • 缺点就是微分系数过大时会卡顿，因为D项权重太大，导致PI想发生变化时,D项想让变化慢一点，阻止了PI产生的变化，导致卡顿
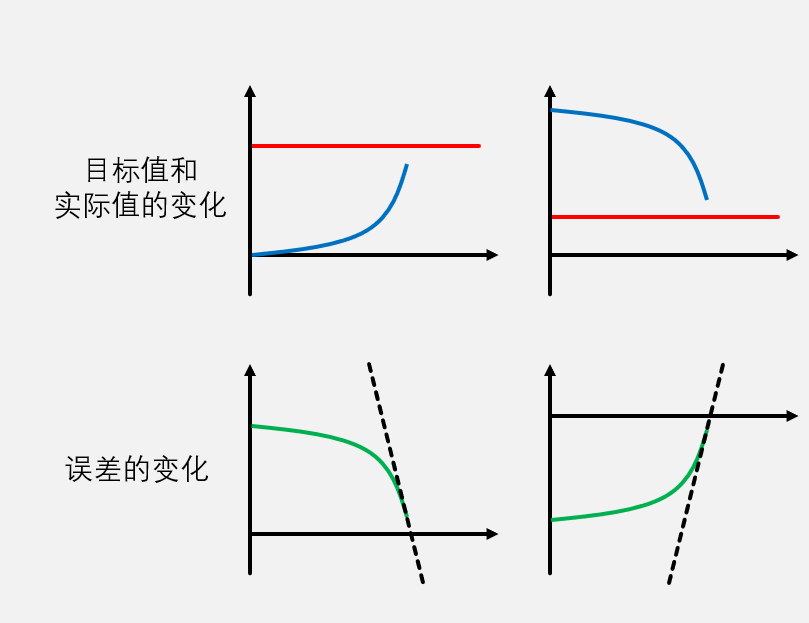
    在这里插入图片描述
  • 蓝色曲线为实际值，红色为目标值，绿色为误差值（红色-蓝色）
  • 上面两个中蓝线都是越接近目标值变化越快，这种就一定要加D项
  • 下面两个图也能看出来误差变化太快需要D项帮助
    在这里插入图片描述
    这就很明显了，第一个图中只有PI作用，那么每当有误差时，PI的调节就会超调导致误差更大，越调越超调，离目标值越来越远，但是加上D项之后就发现会离目标值越来越近，而且微分系数越大阻尼越大，阻尼振荡越来越小

3.离散PID&程序实现思路

连续和离散形式PID

在这里插入图片描述

  • 连续PID需要用模拟电路实现，不断进行计算和调控
  • 离散PID则是一个周期进行一次PID计算和调控
  • 对离散形式PID的理解:
  • 比例项：这里的k表示第k次调控，P项也就是比例系数乘以第k次的调控时刻的误差
  • 积分项：看下面这个图就是连续和离散化的区别，第一个图就是积分的定义，其实就是蓝色矩形面积之和，T就是宽（T越小求和越准确），error(j)就是长，乘积就是面积，j是一个临时变量用于使用循环求和
  • 微分项：某一点的微分就是斜率，这里也是使用两点来计算斜率，T也是越小计算结果越精准
    在这里插入图片描述

位置式PID和增量式PID

在这里插入图片描述

  • 位置式PID能够应用于各种场景
  • 增量式PID其实就是相邻两次PID之间的差值
    在这里插入图片描述
  • 两者的区别：位置式可直接给被控对象，增量式需要被控对象有积分功能，也就是需要被控对象拥有记录上一次状态的功能，才能在此基础上根据增量改变
  • 两者直接皆可以实现相互转化
  • 位置式PID输出的得到的是全量输出值，如果有噪声干扰，不同输出值相差会很大，导致执行机构大幅度变化；增量式PID则可以单独对输出值增量进行限幅，防止执行机构大幅度变化
  • 增量式PID适合自动控制和手动控制切换的场景，自动控制也就是使用PID，手动控制也就是不使用PID，当你将三个参数全部给0时就是自动控制，这个时候如果是位置式电机会由于参数为0输出值也立马变为0，点击停转，但是增量式具有存储上一个输出量的功能，输出值可以位置在当前值所以不会停，这个时候就可以手动调节输出值

PID程序实现

首先确定周期T的值，不能太快也不能太慢，太慢起不到平衡作用，太快硬件传感器分辨率受限,以下是三种实现每隔时间T实现一次PID调控的方法
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
第一个方法最简单但是阻塞式弊端太多；第二个方法定时中断一般最常用，但是要注意不能在中断和主函数里操作同一个硬件，避免资源访问冲突； 第三种也是定时中断，但是自定义标志位可以在主函数里执行PID调控，该方法主程序一定不能阻塞了

位置式PID程序的实现思路
在这里插入图片描述

  • 输出限幅是因为怕PID的输出值超过了硬件的接受范围，所以设置一个接受的上下限

增量式PID程序的实现思路
在这里插入图片描述

  • 这里是控制器内积分得到out而不是out的增量

4.常见优化算法方法

在这里插入图片描述

积分限幅（只用于位置式）

在这里插入图片描述

  • 造成原因：断电或者电机卡死等原因会使电机的实际速度为0，和目标值相差过大，导致积分项会一直无限制积分，而此时一旦又通电，由于积分项太大了电机会满速运转，直到积分项反向积分使电机转速实际值与目标值重合，此时改变目标值才会有效果，在此之前无论如何修改目标值都没用。电机通电满速运转一段时间且无法控制是危险的
  • 实现思路：限制误差积分的增大上限，也就是哪电机停转了，也不能让积分项一直增大，而是增大到一定值就停止增大
  • 阈值设置：最大阈值也就是让积分项=最大输出值，此时误差积分=最大out值/Ki
    在这里插入图片描述

积分分离（定位置）

在这里插入图片描述

  • 常见的都是定速使用PI，定位置用于PD就够了，当定位置使用PD时会发现实际值与目标值总会有那么一点点误差无法消除，是因为理论上只要有PWM电机就会动，但是实际上有摩擦力，PWM很小时驱动力只能够平衡摩擦力，推不动电机旋转，导致一点点的稳态误差，我们也知道积分项可以用来消除稳态误差，实际上确实可以，但是用于定位置控制时又会出现更大的问题——超调，而且这个超调微分项不能解决
  • 使用积分项的超调原因：理论上定位置不存在稳态误差，因为摩擦力基本可以忽略不计，我们只使用比例项完全就够用了，因为定位置最后OUT输出值也为0，电机不旋转，也就是比例项的输出值刚好就是整个OUT输出值（OUTp=OUT），此时加上积分项后，就会是OUTp+OUTi>OUT，这就会导致超调，实际图像就是下图所示，会先超过目标值，然后此时比例项迅速反应并进行反向积分，积分项会迅速反向积分，当积分项正向积分与反向积分抵消时，此时比例项才会使误差为0
    在这里插入图片描述
  • 解决方法：当误差大时使用PD，误差很小时使用PID，防止积分项一直积分导致驱动力不可避免的过大导致超调，如果只在后半段接近目标值才积分，积分时间很短，积分项很小不会产生过大驱动力导致超调
    在这里插入图片描述
  • 分离阈值的设置：使用外力施加于电机并观察波形，使用较大外力时，此时误差会很大，此时阈值比误差值大一点就行，太小了会导致当外力迅速变化时积分项迅速为0，导致此时无积分项来抗衡外力；太大了会导致积分项还是太大了导致超调

变速积分

在这里插入图片描述

  • 变速积分其实就是积分分离的升级版，积分分离是只存在有积分项和无积分项两种情况，变速积分则是积分项大小会随误差大小变化而变化，麻烦的是需要设置一个函数表示变化关系，如果函数不好的话，效果甚至不如积分分离
    在这里插入图片描述
    在这里插入图片描述

微分先行

在这里插入图片描述
在这里插入图片描述

  • 当目标值突然变化时，微分项是误差的斜率，也就是起初微分项接近正无穷大，后面误差变化正常，斜率是负的反向微分而且微分项会越来越小
    在这里插入图片描述
  • 目标值频繁切换导致数据产生尖峰，且Kd越大尖峰越高，按理来说只存在微分项时，只改变目标值电机不会旋转，因为微分项只起到给实际值添加阻尼效果，应该不具备输出能力，但是实际上纯微分项控制时电机会由于误差快速变化导致旋转，那么其实可以只对实际值进行微分，无论误差如何变化，此时微分项就只起到加阻尼效果而不具备输出能力，而且实际值也不会突变。在计算误差进行PI之前提前对实际值进行微分，这就是微分先行的原理
  • 但是实际情况要看使不使用微分先行，因为微分项可以帮助比例项更快响应目标值变化，尤其是误差较大的变化，如果只需要微分项起到阻尼效果可以加微分先行
    在这里插入图片描述

不完全微分

在这里插入图片描述
在这里插入图片描述

  • 观察上面的图，红色曲线代表噪声，绿色曲线是理想值，噪声对比例项来说影响很小，就是噪声和理想值的误差值之差，一般噪声和理想值不会相差很大；对积分项来说就是曲线下的面积，噪声有时候比理想值高有时候也有低的时候，所以实际面积两者相差不大；微分项代表斜率，看图可知理想值的斜率为正的时候，噪声可能直接为负值了，这个影响就很大，所以需要过滤噪声也就是添加滤波器，也就是不完全微分
  • 之所以不对开始的值全部滤波，是因为滤波会增加时延，导致PID响应速度变慢
  • 不完全微分的微分项就是本次微分项和上次微分项占不同权重然后加起来得到新的微分项，a取0.5相当于均值滤波，a越大本次微分项权重越低，滤波效果就越好
  • 一阶惯性单元滤波公式：假设输入是x(k),输出是y(k),则有y(k)=(1-a)x(k)+ay(k-1),意思是本次输出为本次输入和上次输出的加权平均值
    在这里插入图片描述

输出偏移

在这里插入图片描述

  • 也就是PWM要么就不输出，一旦输出，该PWM就一定要能驱动电机
  • 偏移量需要单独写一个测试程序测量
  • 缺点就是很难稳定，因为PID但凡调控电机必定转动，目标值与实际值会一直存在误差很难为0，甚至目标值都在抖动有噪声，所以就会一直抖动
    在这里插入图片描述

输入死区

在这里插入图片描述

  • 死区阈值
    在这里插入图片描述

注意事项

  • 积分限幅一般都要使用
  • 微分项可以帮助比例项更快响应目标值变化，尤其是误差较大的变化，如果只需要微分项起到阻尼效果可以加微分先行
  • 输出偏移+输入死区可以将误差控制在可接受范围，但是积分分离可以无误差，但是会有积分项的滞后性
  • 滤波有延时性，滤波效果越好延时一般越严重

5.双环PID基本原理

串级PID简介

在这里插入图片描述

  • 关键所在：使用外环PID的输出值作为内环PID的目标值，但是内外环的PID的实际值都会返还给当前环
  • 可以对更多物理量进行控制，性能更好，比如可以实现点击定速定位控制，也就是让电机以指定速度来到指定位置停下来

单双环对比

在这里插入图片描述

  • 双环PID相当于单环PID自带一个定速控制的电机，而且位置环想控制位置时输出一个值给速度环，当实际位置与目标位置越接近时，位置环输出越小，速度环目标速度也就越小直到为0，此时电机达到指定位置而且速度也为0
  • 不存在启动力度过小电机转不起来的问题，因为位置环的目标位置设置很小时输出值给到了PI控制的速度环，由于是PI控制那么只要有目标速度而且目标位置与实际位置存在误差电机一定为转动而且最终会与目标位置重合
  • 抵抗外力的作用更强，因为施加外力时，速度环的目标速度应该为0，却由于外力产生实际速度，有了误差就会PI调控产生一个阻力对抗外力，而且又存在位置环，施加外力导致位置改变，位置环又要产生负向输出值给到速度环，让速度环的误差变大，速度环的积分项就会更大从而产生更大的对抗力
  • 优点也就是响应速度快，稳定性好，准确性高
  • 调参顺序：先内环后外环
    在这里插入图片描述
  • 内环和外环调控周期可以不同，可以设计总PID调控周期，然后在里面分别设置内环外环的调控周期
  • 一般外环调控周期大于或等于内环，一是因为外环输出值刷新很快内环读取不过来没什么意义，二是因为内环一般调控反应更快的物理量，频率更大
  • 需要修改内环PID的积分阈值，为外环的目标值的阈值，然后加上InnerTarget=OuterOut
  • 修改内环参数时，先要取消外环对内环的控制，也就是注释这一句InnerTarget=OuterOut
  • 修改内环的速度可以修改内环数值的积分限幅幅值

6.调参技巧

  • Kp：不断改变目标值观察实际值，然后逐步增大Kp直到实际值开始抖动，然后适当减小KP让抖动消失，此时Kp就比较适合
  • Ki ：看消除稳态误差的速度不满不满意，不满意就加大Ki但是不能够出现大幅度超调
  • Kd：太大会出现振荡，调节PD时，可以将P参数给大一点也没啥，超调可以用D来调节但是不能振荡，如果振荡就要调小KP
  • 三个参数的值建议量程显示大一点，尤其是使用电位器时候由于电位器的抖动，三个参数并不能完全为0，会出现实际值仍然缓慢跟踪目标值，量程够大的话能够看见应该不是0
  • 学会取舍，参数越响应快但是抖动振荡越严重，参数小响应慢但是动作平滑

代码部分

PID.c

#include "stm32f10x.h"                  // Device header
#include "PID.h"void PID_Update(PID_t *p)
{p->Error1 = p->Error0;p->Error0 = p->Target - p->Actual;if (p->Ki != 0){p->ErrorInt += p->Error0;}else{p->ErrorInt = 0;}p->Out = p->Kp * p->Error0+ p->Ki * p->ErrorInt+ p->Kd * (p->Error0 - p->Error1);if (p->Out > p->OutMax) {p->Out = p->OutMax;}if (p->Out < p->OutMin) {p->Out = p->OutMin;}
}

PID.h

#ifndef __PID_H
#define __PID_Htypedef struct {float Target;float Actual;float Out;float Kp;float Ki;float Kd;float Error0;float Error1;float ErrorInt;float OutMax;float OutMin;
} PID_t;void PID_Update(PID_t *p);#endif

相关文章：

STM32江科大----------PID算法

声明&#xff1a;本人跟随b站江科大学习&#xff0c;本文章是观看完视频后的一些个人总结和经验分享&#xff0c;也同时为了方便日后的复习&#xff0c;如果有错误请各位大佬指出&#xff0c;如果对你有帮助可以点个赞小小鼓励一下&#xff0c;本文章建议配合原视频使用❤️ 如…...

编程日记 2025/8/25 14:21:40

计算机视觉相机模型与标定：如何让计算机“看懂”三维世界？

计算机视觉相机模型与标定：如何让计算机“看懂”三维世界？ 一、前言二、相机模型基础​2.1 针孔相机模型​2.1.1 模型原理​2.1.2 代码示例​2.2 透视变换与相机内参​2.2.1 透视变换矩阵​2.2.2 内参矩阵的作用​2.3 相机外参​2.3.1 世界坐标系与相机坐标系的转换​2.3.2 外…...

编程日记 2025/8/20 15:27:58

ETL数据集成平台在制造业有哪些应用场景

在制造业的数字化转型中&#xff0c;数据如同散落的拼图——生产线的实时参数、供应链的物流轨迹、质量检测的海量报告……每一块都承载着关键信息&#xff0c;却因系统割裂、格式混乱而难以拼出完整价值图谱。如何让数据从“成本负担”变为“战略资产”&#xff1f;ETL&#x…...

编程日记 2025/8/24 7:42:53

Redis-07-常见Redis使用场景

文章目录 01.缓存数据&#xff08;Cache&#xff09;02.布式锁&#xff08;Distributed Lock&#xff09;03.计数器&#xff08;Counter&#xff09;04.排行榜&#xff08;Leaderboard&#xff09;05.消息队列&#xff08;Message Queue&#xff09;06.限流&#xff08;Rate Li…...

编程日记 2025/8/24 6:34:20

开源模型应用落地-Podcastfy-从文本到声音的智能跃迁-Gradio（一）

一、前言 在当今信息呈现方式越来越多样化的背景下&#xff0c;如何将文字、图片甚至视频高效转化为可听的音频体验&#xff0c;已经成为内容创作者、教育者和研究者们共同关注的重要话题。Podcastfy是一款基于Python的开源工具&#xff0c;它专注于将多种形式的内容智能转换成…...

编程日记 2025/8/24 8:17:30

【AI News | 20250416】每日AI进展

AI Repos 1、Tutorial-Codebase-Knowledge 自动分析 GitHub 仓库并生成适合初学者的通俗易懂教程&#xff0c;清晰解释代码如何运行&#xff0c;还能生成可视化内容来展示核心功能。爬取 GitHub 仓库并从代码中构建知识库&#xff1b;分析整个代码库以识别核心抽象概念及其交互…...

编程日记 2025/8/23 2:04:53

iOS内存管理中的强引用问题

iOS内存管理 关于强引用循环 强引用循环是 ARC 无法自动处理的常见问题。如果两个对象互相强引用对方&#xff0c;就会造成引用计数不为零&#xff0c;导致对象无法释放。典型的情况是在闭包中引用 self 时&#xff0c;self 和闭包之间可能会互相持有&#xff0c;形成强引用循…...

编程日记 2025/8/25 11:18:07

电脑一直不关机会怎么样？电脑长时间不关机的影响

现代生活中&#xff0c;许多人会让自己的电脑24小时不间断运行&#xff0c;无论是为了持续的工作、娱乐&#xff0c;还是出于忘记关机的习惯。然而&#xff0c;电脑长时间不关机&#xff0c;除了提供便利之外&#xff0c;也可能对设备的健康产生一系列影响。本文将为大家介绍电…...

编程日记 2025/8/21 7:03:25

openGauss DataVec + Dify，快速搭建你的智能助手平台

在当今数字化和智能化的时代&#xff0c;大语言模型&#xff08;LLM&#xff09;的应用正以前所未有的速度改变着各个领域的工作方式和用户体验。Dify 作为一个开源的大语言模型应用开发平台&#xff0c;为开发者们提供了便捷且强大的工具&#xff0c;助力构建从基础智能体到复…...

编程日记 2025/8/22 23:07:25

React 入门教程：构建第一个 React 应用

本教程将带你从零开始构建你的第一个 React 应用。我们将创建一个简单的计数器应用&#xff0c;涵盖 React 的基本概念和开发流程。 准备工作 在开始之前&#xff0c;请确保你的开发环境满足以下要求&#xff1a; Node.js (建议使用最新的 LTS 版本) npm 或 yarn (Node.js 安…...

编程日记 2025/8/22 3:11:16

【数字图像处理】数字图像空间域增强（3）

图像锐化 图像细节增强 图像轮廓&#xff1a;灰度值陡然变化的部分 空间变化&#xff1a;计算灰度变化程度 图像微分法&#xff1a;微分计算灰度梯度突变的速率 一阶微分&#xff1a;单向差值 二阶微分&#xff1a;双向插值 一阶微分滤波 1&#xff1a;梯度法 梯度&#xff1…...

编程日记 2025/8/25 12:45:18

mapstruct使用详解

一、背景&#xff1a;为什么需要 mapstruct 在 Java 开发中&#xff0c;对象之间的映射&#xff08;如 DTO 转实体类、实体类转 VO&#xff09;是一项高频且繁琐的任务。手动编写映射代码存在以下问题&#xff1a; 冗余代码多&#xff1a;每个类都需要重复编写 setter 和 get…...

编程日记 2025/8/24 20:50:54

Token与axios拦截器

目录 一、Token 详解 1. Token 的定义与作用 2. Token 的工作流程 3. Token 的优势 4. Token 的安全实践 5. JWT 结构示例 二、Axios 拦截器详解 1. 拦截器的作用 2. 请求拦截器 3. 响应拦截器 4. 拦截器常见场景 5. 移除拦截器 三、完整代码示例 四、总结 五、…...

编程日记 2025/8/21 16:03:26

windows上安装Jenkins

1. 下载windows版 jenkins安装包 2. 配置本地安全策略 在 Windows 11/10 上打开本地安全策略。 Secpol.msc 或本地安全策略编辑器是一个 Windows 管理工具&#xff0c;允许您在本地计算机上配置和管理与安全相关的策略。 安全设置-》本地策略-》用户权限分配-》作为服务登录…...

编程日记 2025/8/24 1:04:21

鸿蒙NEXT开发文件预览工具类（ArkTs）

import { uniformTypeDescriptor } from kit.ArkData; import { filePreview } from kit.PreviewKit; import { FileUtil } from ./FileUtil; import { AppUtil } from ./AppUtil; import { WantUtil } from ./WantUtil;/*** 文件预览工具类* 提供文件预览、加载、判断等功能。…...

编程日记 2025/8/23 23:09:06

【WPF-VisionMaster源代码】应用OpenCVSharp仿Vision Master页面开发的软件源代码

一、目的&#xff1a;开放WPF-VisionMaster源代码 二、简介 WPF-Vision Master 视觉处理软件源码 WPF-Vision Master是基于WPF-Control的UI框架与OpenCVSharp计算机视觉库联合&#xff0c;并参考Vision Master界面开发的视觉处理软件。该平台深度融合WPF强大的界面控制能力和Op…...

编程日记 2025/8/23 22:20:18

软件研发过程中的技术债

引言&#xff1a;数字时代的“技术利息” 在金融领域&#xff0c;债务是推动发展的杠杆&#xff1b;而在软件开发中&#xff0c;技术债&#xff08;Technical Debt&#xff09;却是一把双刃剑。据行业调查显示&#xff0c;70%的软件项目存在技术债&#xff0c;其中超过半数团队…...

编程日记 2025/8/25 14:14:16

鸿蒙应用（医院诊疗系统）开发篇2·Axios网络请求封装全流程解析

一、项目初始化与环境准备 1. 创建鸿蒙工程 src/main/ets/ ├── api/ │ ├── api.ets # 接口聚合入口 │ ├── login.ets # 登录模块接口 │ └── request.ets # 网络请求核心封装 └── pages/ └── login.ets # 登录页面逻辑…...

编程日记 2025/8/24 15:10:55

重新定义“边缘”：边缘计算如何重塑人类与数据的关系

在数字化浪潮中&#xff0c;云计算曾是科技界的宠儿&#xff0c;但如今&#xff0c;边缘计算正在悄然改变游戏规则。它不仅是一种技术进步&#xff0c;更是对人类与数据关系的一次深刻反思。本文将探讨边缘计算如何从“中心化”走向“分布式”&#xff0c;以及它如何在效率、隐…...

编程日记 2025/8/24 19:42:59

Flink CDC 出现错误码 1236 和 SQL 状态 HY000 的原因及解决方法

Flink CDC 出现错误码 1236 和 SQL 状态 HY000 的原因及解决方法 常见原因 server-id 冲突：当多个 Flink CDC 任务连接同一个 MySQL 实例，且使用了相同的 server-id 时，会导致该冲突。因为 MySQL 服务器通过 server-id 来区分不同的从服务器，如果多个 Flink CDC 任务使用相…...

编程日记 2025/8/17 12:08:24

如何解除Excel只读状态？4种方法全解析

在日常办公中&#xff0c;我们经常会遇到Excel文件被设置为只读模式的情况。只读模式可以防止文件被意外修改&#xff0c;但在需要编辑时&#xff0c;解除只读模式就显得尤为重要。下面小编分享退出Excel只读方式的4种方法&#xff0c;让你能够轻松编辑工作表。 方法1&#xf…...

编程日记 2025/8/24 2:01:15

深度学习与 Flask 应用常见问题解析

在深度学习和 Flask 应用开发过程中&#xff0c;我们常常会遇到一些关键的知识点和容易混淆的问题。下面我们就来对这些问题进行详细的解析。 一、卷积神经网络&#xff08;CNN&#xff09;常用层 在定义卷积神经网络时&#xff0c;有一些常用的层&#xff1a; Conv2D&#x…...

编程日记 2025/8/20 8:23:50

零浪费，最高效率：通往0%废品率的道路

在工业自动化领域&#xff0c;努力实现废品率为 0% 是最大的挑战之一。这意味着不生产任何有缺陷的产品 —— 从而减少浪费、降低成本&#xff0c;并提高客户满意度。尽管实现这一目标颇具雄心壮志&#xff0c;但企业可以采取几个步骤来改进自身流程&#xff0c;以达成这一目标…...

编程日记 2025/8/24 8:53:25

【c++深入系列】：new和delete运算符详解

&#x1f525; 本文专栏&#xff1a;c &#x1f338;作者主页&#xff1a;努力努力再努力wz &#x1f4aa; 今日博客励志语录&#xff1a; “生活不会向你许诺什么&#xff0c;尤其不会向你许诺成功。它只会给你挣扎、痛苦和煎熬的过程。但只要你坚持下去&#xff0c;终有一天&…...

编程日记 2025/8/23 21:38:49

基础（测试用例：介绍，测试用例格式，案例）

目录 测试用例介绍 测试用例编写格式 案例 测试用例介绍 用例&#xff1a;用户使用软件的案例场景 测试用例&#xff1a;是为测试项目而设计的测试执行文档 测试用例的作用&#xff1a; 防止漏测是实施测试的标准可以作为测试工作量的评估 测试用例编写格式 用例编号 用例…...

编程日记 2025/8/24 8:17:32

MCP协议，.Net 使用示例

服务器端示例 基础服务器 以下是一个基础的 MCP 服务器示例&#xff0c;它使用标准输入输出&#xff08;stdio&#xff09;作为传输方式&#xff0c;并实现了一个简单的回显工具&#xff1a; using Microsoft.Extensions.DependencyInjection; using Microsoft.Extensions.H…...

编程日记 2025/8/24 22:52:24

Node.js 数据库 事务 项目示例

1、参考&#xff1a;JavaScript语言的事务管理_js 函数 事务性-CSDN博客 或者百度搜索&#xff1a;Nodejs控制事务&#xff0c; 2、实践 2.1、对于MySQL或MariaDB&#xff0c;你可以使用mysql或mysql2库&#xff0c;并结合Promise或async/await语法来控制事务。 使用 mysql2…...

编程日记 2025/8/19 16:56:33

【AI插件开发】Notepad++ AI插件开发实践：支持多平台多模型

引言 上篇文章我们的Notepad插件介绍到Dock窗口集成&#xff0c;本篇将继续完善插件功能&#xff0c;主要包括两个部分&#xff1a; 支持多平台、多模型支持多种授权验证、接口类型 一、多平台 原先的配置项很简单&#xff1a; // PluginConf.h class PlatformConf { publ…...

编程日记 2025/8/24 8:26:50

微信小程序数字滚动效果

效果图 .wxml <view class"container"><view class"container-num" wx:for"{{number}}" wx:key"index"><view class"num-container" style"--h:{{h}}px;--y:{{-item * h }}px;"><view wx:f…...

编程日记 2025/8/24 0:04:42

wx219基于ssm+vue+uniapp的教师管理系统小程序

开发语言&#xff1a;Java框架&#xff1a;ssmuniappJDK版本&#xff1a;JDK1.8服务器&#xff1a;tomcat7数据库&#xff1a;mysql 5.7&#xff08;一定要5.7版本&#xff09;数据库工具&#xff1a;Navicat11开发软件&#xff1a;eclipse/myeclipse/ideaMaven包&#xff1a;M…...

编程日记 2025/8/22 20:10:20

Python 注释进阶之Google风格

文章目录 1. Google 风格 Docstring 的核心特点2. Google 风格的基本结构3. 编写规则和注意事项4. 最常用的 Google 风格 Docstring 示例示例 1&#xff1a;普通函数 示例 2&#xff1a;带默认参数和可变参数的函数示例 3&#xff1a;类示例 4&#xff1a;生成器函数示例 5&…...

编程日记 2025/8/22 23:16:55

写测试文档时，需要的环境配置怎么查看

操作系统 cat /etc/os-releaseCPU信息 lscpu 内存 sudo dmidecode --type memory | grep -E "Size:|Type:|Speed:"硬盘 列出当前系统中 所有块设备&#xff08;Block Devices&#xff09; 的信息&#xff0c;并显示指定列&#xff08;-o 参数&#xff09; lsblk…...

编程日记 2025/8/19 2:47:49

强化学习的数学原理（十）actor-critic 方法

由于全文太长&#xff0c;只好分开发了。(已完结&#xff01;在专栏查看本系列其他文章&#xff09; 个人博客可以直接看全文~ 本系列为在学习赵世钰老师的“强化学习的数学原理” 课程后所作笔记。 课堂视频链接https://www.bilibili.com/video/BV1sd4y167NS/ 第十章 acto…...

编程日记 2025/8/19 7:34:49

多个定时器同时工作时，会出现哪些常见的bug ，如何解决？？（定时任务未实时更新但刷新后正常的问题分析）

1. 定时器冲突与覆盖 问题&#xff1a;后设置的定时器可能覆盖先前的定时器&#xff0c;导致前一个定时器失效 原因&#xff1a;未正确管理定时器ID或未清除前一个定时器 2. 性能问题 内存泄漏&#xff1a;未清除不再需要的定时器会导致内存占用不断增加 CPU过载&#xff1a…...

编程日记 2025/8/21 18:22:32

代码随想录算法训练营day5（哈希表）

华子目录 有效的字母异位词思路 有效的字母异位词 https://leetcode.cn/problems/valid-anagram/description/ 思路 使用哈希表&#xff0c;这里哈希表使用数组先申请一个26空间的大小的数组遍历第一个字符串&#xff0c;记录每个字符出现的次数1遍历第二个字符串&#xff0c…...

编程日记 2025/8/22 8:51:33

Python（17）Python字符编码完全指南：从存储原理到乱码终结实战

目录 背景介绍一、字符编码核心原理1. 计算机存储本质2. Python3的编码革命3. 主流编码格式对比 二、编码转换核心方法1. 编码&#xff08;Encode&#xff09;过程2. 解码&#xff08;Decode&#xff09;过程3. 错误处理策略 三、文件操作编码实战1. 文本文件读写2. 二进制模式…...

编程日记 2025/8/22 17:11:56

Node.js 文件读取与复制相关内容

Node.js 文件读取与复制相关内容的系统总结&#xff0c;包括 同步读取、异步读取、流式读取、复制操作、两者对比及内存测试。 &#x1f9e9; 一、Node.js 文件读取方式总结 Node.js 使用 fs&#xff08;文件系统&#xff09;模块进行文件操作&#xff1a; 1. 同步读取&#…...

编程日记 2025/8/24 8:49:26

大数据面试问答-HBase/ClickHouse

1. HBase 1.1 概念 HBase是构建在Hadoop HDFS之上的分布式NoSQL数据库&#xff0c;采用列式存储模型&#xff0c;支持海量数据的实时读写和随机访问。适用于高吞吐、低延迟的场景&#xff0c;如实时日志处理、在线交易等。 RowKey&#xff08;行键&#xff09; 定义&#xf…...

编程日记 2025/8/20 21:44:56

jupyter 文件浏览器，加强版，超好用，免费exe

第一步&#xff1a;github搜索 lukairui的 jupyter-viewer-plus 仓库 第二步&#xff1a; git clone 到本地。 解压zip包 第三步&#xff1a; 进入压缩包&#xff0c;第一次双击打开jupyter-viewer-plus.exe运行&#xff0c;第一次运行后&#xff0c;界面上有一个“设为…...

编程日记 2025/8/17 20:53:40

【AI工具】用大模型生成脑图初试

刚试用了一下通过大模型生成脑图&#xff0c;非常简单&#xff0c;记录一下 一、用大模型生成脑图文件 关键&#xff1a;存在markdown文件 举例&#xff1a;使用Deepseek&#xff0c;输入问题&#xff1a;“针对大模型的后训练&#xff0c;生成一个开发计划&#xff0c;用ma…...

编程日记 2025/8/23 13:59:09

数据结构-树与二叉树

一、树的定义与基本术语 1.1 树的定义 树&#xff08;Tree&#xff09;是一种非线性的数据结构&#xff0c;它是由 n&#xff08;n ≥ 0&#xff09;个有限节点组成的集合。如果 n 0&#xff0c;称为空树&#xff1b;如果 n > 0&#xff0c;则&#xff1a; 有一个特定的节…...

编程日记 2025/8/25 1:01:46

STL_unordered_map_01_基本用法

&#x1f44b; Hi, I’m liubo&#x1f440; I’m interested in harmony&#x1f331; I’m currently learning harmony&#x1f49e;️ I’m looking to collaborate on …&#x1f4eb; How to reach me …&#x1f4c7; sssssdsdsdsdsdsdasd&#x1f383; dsdsdsdsdsddfsg…...

编程日记 2025/8/23 5:00:15

ARCGIS国土超级工具集1.5更新说明

ARCGIS国土超级工具集V1.5版本更新说明&#xff1a;因作者近段时间工作比较忙及正在编写ARCGISPro国土超级工具集&#xff08;截图附后&#xff09;的原因&#xff0c;故本次更新为小更新&#xff08;没有增加新功能&#xff0c;只更新了已有的工具&#xff09;。本次更新主要修…...

编程日记 2025/8/21 6:40:28

主流物理仿真引擎和机器人/强化学习仿真平台对比

以下是当前主流的物理仿真引擎和机器人/强化学习仿真平台的特点和适用场景&#xff0c;方便根据需求选择&#xff1a; &#x1f9e0; NVIDIA 系列 ✅ Isaac Lab v1.4 / v2 特点&#xff1a; 基于 Omniverse Isaac Sim&#xff0c;属于高端视觉机器人仿真框架v2 更加模块化&a…...

编程日记 2025/8/24 14:58:46

STM32 HAL库内部 Flash 读写实现

一、STM32F407 内部 Flash 概述 1.1 Flash 存储器的基本概念 Flash 存储器是一种非易失性存储器&#xff0c;它可以在掉电的情况下保持数据。STM32F407 系列微控制器内部集成了一定容量的 Flash 存储器&#xff0c;用于存储程序代码和数据。Flash 存储器具有擦除和编程次数的…...

编程日记 2025/8/20 8:30:26

C++学习：六个月从基础到就业——面向对象编程：构造函数与析构函数

C学习&#xff1a;六个月从基础到就业——面向对象编程&#xff1a;构造函数与析构函数 本文是我C学习之旅系列的第十篇技术文章&#xff0c;主要讨论C中构造函数与析构函数的概念、特点和使用技巧。这些是C对象生命周期管理的关键组成部分。查看完整系列目录了解更多内容。 引…...

编程日记 2025/8/24 1:17:01

dfs二叉树中的深搜(回溯、剪枝)--力扣129、814、230、257

目录 1.1题目链接&#xff1a;129.求根节点到叶结点数字之和 1.2题目描述&#xff1a;给你一个二叉树的根节点 root &#xff0c;树中每个节点都存放有一个 0 到 9 之间的数字。 1.3解法(dfs-前序遍历)&#xff1a; 2.1题目链接&#xff1a;814.二叉树剪枝 2.2题目描述&…...

编程日记 2025/8/22 7:53:59

Python Selenium 一小时速通教程

Python Selenium 一小时速通教程 实战案例 一、环境配置&#xff08;10分钟&#xff09; 安装Python 确保已安装Python 3.x&#xff08;官网下载&#xff09;。 安装Selenium 在终端运行&#xff1a; pip install selenium下载浏览器驱动 Chrome&#xff1a;访问 ChromeDriv…...

编程日记 2025/8/25 12:27:25

通过GO后端项目实践理解DDD架构

最近在工作过程中重构的项目要求使用DDD架构&#xff0c;在网上查询资料发现教程五花八门&#xff0c;并且大部分内容都是长篇的概念讲解&#xff0c;晦涩难懂&#xff0c;笔者看了一些github上入门的使用DDD的GO项目&#xff0c;并结合自己开发中的经验&#xff0c;谈谈自己对…...

编程日记 2025/8/22 15:55:20

MybatisPlus最新版分页无法使用

在使用分页的时候发现分页拦截器关键API会报错&#xff0c;其实根本原因是在之前只需要导入一个mybatisplus依赖&#xff0c;而现在分页似乎被单独分离出来了&#xff0c;需要额外导入新依赖使其支持 ​ <dependency><groupId>com.baomidou</groupId><art…...

编程日记 2025/8/24 2:01:24