dfs二叉树中的深搜(回溯、剪枝)--力扣129、814、230、257

目录

1.1题目链接：129.求根节点到叶结点数字之和

1.2题目描述：给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。

1.3解法(dfs-前序遍历)：

2.1题目链接：814.二叉树剪枝

2.2题目描述：

2.3解法(dfs-后序遍历)：

3.1题目链接：98.验证二叉搜索树

3.2题目描述：

3.3解法(利用中序遍历)

4.1题目链接：230.二叉搜索树中第K小的元素

4.2题目描述：

4.3解法(中序遍历+计数器剪枝)

5.1题目链接：257.二叉树的所有路径

5.2题目描述：

5.3解法(回溯)：

---

本文提供了四道关于二叉树的问题及它们的解法：

1. 求根节点到叶结点数字之和：给定一个二叉树，树中每个节点存放一个0到9之间的数字，求从根节点到叶节点生成的所有数字之和。解法使用深度优先搜索（DFS）的前序遍历，整合父节点信息与当前节点信息计算当前节点数字，并递归向下传递，在叶子节点处返回结果。

2. 二叉树剪枝：给定一个二叉树，节点值为0或1，返回移除所有不包含1的子树的原二叉树。解法使用DFS的后序遍历，逐步删除叶子节点，保证删除后节点仍满足条件。

3. 验证二叉搜索树：判断给定二叉树是否是有效的二叉搜索树。解法利用中序遍历，递归判断左子树是否为BST，当前节点是否满足BST条件，以及右子树是否为BST。

4. 二叉搜索树中第K小的元素：在二叉搜索树中查找第K小的元素。解法使用中序遍历配合计数器进行剪枝，当计数器等于0时找到第K小的元素。

此外，还提供了第5道题目二叉树的所有路径，返回所有从根节点到叶子节点的路径的解法，使用回溯法将路径存储在结果中。

1.1题目链接：129.求根节点到叶结点数字之和

1.2题目描述：
给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。

每条从根节点到叶节点的路径都代表一个数字：

• 例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。

计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

示例 1：

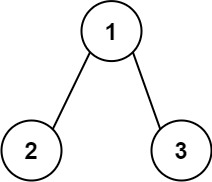
输入：root = [1,2,3]
输出：25
解释：
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此，数字总和 = 12 + 13 = 25

示例 2：

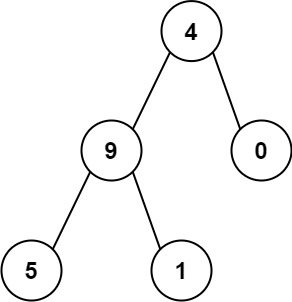
输入：root = [4,9,0,5,1]
输出：1026
解释：
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此，数字总和 = 495 + 491 + 40 = 1026

提示：

• 树中节点的数目在范围 [1, 1000] 内
• 0 <= Node.val <= 9
• 树的深度不超过 10

1.3解法(dfs-前序遍历)：

前序遍历按照根结点、左子树、右子树的顺序遍历二叉树的所有结点，通常用于子节点的状态依赖于父节点状态的题目。

算法思路：

在前序遍历的过程中，我们可以往左右子树传递信息，并且在回溯时得到左右子树的返回值。递归函数可以帮我们完成两件事：

1. 将父节点的数字与当前结点的信息整合到一起，计算出当前结点的数字，然后传递到下一层进行递归；
2. 当遇到叶子结点的时候，就不再向下传递信息，而是将整合的结果向上一直回溯到根节点。

当递归结束时，根结点需要返回的值也就被更新为了整棵数的数字和。

算法流程：
递归函数设计：int dfs(TreeNode* root, int num)

1. 返回值：当前子树计算的结果(数字和)；
2. 参数num：递归过程中往下传递的信息(父结点的数字)
3. 函数作用：整合父节点的信息与当前结点的信息计算当前结点数字，并向下传递，在回溯时返回当前子树(当前结点作为子树根结点)数字和

递归函数流程：

1. 当遇到空节点的时候，说明这条路从根节点开始没有分支，返回0
2. 结合父节点传下的信息以及当前节点的val，计算出当前节点数字sum
3. 如果当前节点是叶子节点，直接返回整合后的结果sum
4. 如果当前节点不是叶子节点，将sum传到左右子树中去，得到左右子树中节点路径的数字和，然后相加返回结果。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int sumNumbers(TreeNode* root) {return dfs(root,0);}int dfs(TreeNode* root, int sum){sum = sum*10 + root->val;if(root->left == nullptr && root->right == nullptr){return sum;}int ret = 0;if(root->left)ret += dfs(root->left, sum);if(root->right)ret += dfs(root->right, sum);return ret;}
};

2.1题目链接：814.二叉树剪枝

2.2题目描述：

给你二叉树的根结点 root ，此外树的每个结点的值要么是 0 ，要么是 1 。

返回移除了所有不包含 1 的子树的原二叉树。

节点 node 的子树为 node 本身加上所有 node 的后代。

示例 1：

输入：root = [1,null,0,0,1]
输出：[1,null,0,null,1]
解释：
只有红色节点满足条件“所有不包含 1 的子树”。 右图为返回的答案。

示例 2：

输入：root = [1,0,1,0,0,0,1]
输出：[1,null,1,null,1]

示例 3：

输入：root = [1,1,0,1,1,0,1,0]
输出：[1,1,0,1,1,null,1]

提示：

• 树中节点的数目在范围 [1, 200] 内
• Node.val 为 0 或 1

2.3解法(dfs-后序遍历)：

后序遍历按照左子树、右子树、根节点的顺序遍历二叉树的所有结点，通常用于父节点的状态依赖于子结点状态的题目。

算法思路：

如果我们选择从上往下删除，我们需要收集左右子树的信息，这可能导致代码编写相对困难。然而，通过观察我们可以发现，如果我们先删除最底部的叶子结点，然后再处理删除后的结点，最终的结果并不会受到影响。

因此，我们可以采用后序遍历的方式来解决这个问题。在后序遍历中，我们先处理左子树，然后处理右子树，最后再处理当前节点。在处理当前节点时，我们可以判断其是否为叶子节点且其值是否为0，如果满足条件，我们可以删除当前节点。

• 需要注意的是，在删除叶子节点时，其父节点很可能会成为新的叶子节点。因此，在处理完子节点后，我们仍然需要处理当前节点。这也是为什么选择后序遍历的原因（后序遍历首先遍历到的一定是叶子节点）。
• 通过使用后序遍历，我们可以逐步删除叶子节点，并且保证删除后的节点仍然满足删除操作的要求。这样，我们可以较为方便地实现删除操作，而不会影响最终的结果。
• 若在处理结束后所有叶子节点的值均为1，则所有子树均包含1，此时可以返回。

算法流程：

递归函数设计：void dfs(TreeNode* root)

1. 返回值：无；
2. 参数：当前需要处理的节点
3. 函数作用：判断当前节点是否需要删除，若需要删除，则删除当前节点。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* pruneTree(TreeNode* root) {if(root == nullptr) return nullptr;root->left = pruneTree(root->left);root->right = pruneTree(root->right);if(root->left == nullptr && root->right == nullptr && root->val == 0){delete root;//防止内存泄漏root = nullptr;}return root;}
};

3.1题目链接：98.验证二叉搜索树

3.2题目描述：

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

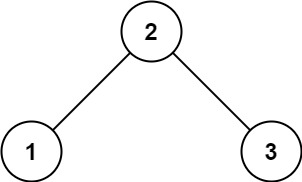
输入：root = [2,1,3]
输出：true

示例 2：

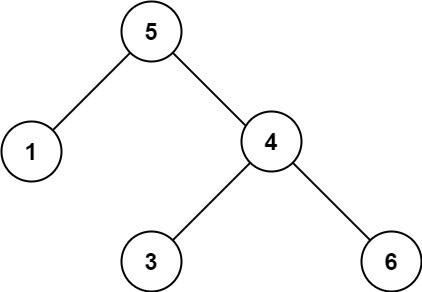
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 10^4] 内
• -2^31 <= Node.val <= 2^31 - 1

3.3解法(利用中序遍历)

后序遍历按照左子树、根节点、右子树的顺序遍历二叉树的所有节点，通常用于二叉搜索树相关题目。
算法思路：
如果一棵树是二叉搜索树，那么它的中序遍历的结果一定是一个严格递增的序列。
因此，我们可以初始化一个无穷小的全区变量，用来记录中序遍历过程中的前驱结点。那么就可以在中序遍历的过程中，先判断是否和前驱结点构成递增序列，然后修改前驱结点为当前结点，传入下一层的递归中。
算法流程：
1. 初始化一个全局的变量 prev，用来记录中序遍历过程中的前驱结点的val；
2. 中序遍历的递归函数中：

• 设置递归出口：root == nullptr的时候，返回true；
• 先递归判断左子树是否是二叉搜索树，用left标记
• 然后判断当前节点是否满足二叉搜索树，用cur标记                                                               如果当前节点的val大于prev，说明满足条件，cur改为true                                                 如果当前节点的val小于等于prev，说明不满足条件，cur改为false                              
• 最后递归判断右子树是否是二叉搜索树，用right标记

3.只有当left，cur，right都是true的时候，才返回true

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int prev;bool isValidBST(TreeNode* root) {if(root == nullptr)return true;bool left = isValidBST(root->left);//剪枝if(left == false)return false;bool cur = false;if(root->val > prev)cur = true;//剪枝if(cur == false)return false;prev = root->val; bool right = isValidBST(root->right);return left&&right&&cur;}
};

4.1题目链接：230.二叉搜索树中第K小的元素

4.2题目描述：

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 小的元素（从 1 开始计数）。

示例 1：

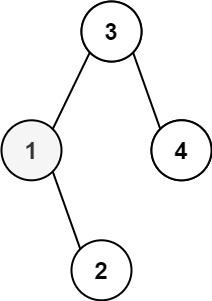
输入：root = [3,1,4,null,2], k = 1
输出：1

示例 2：

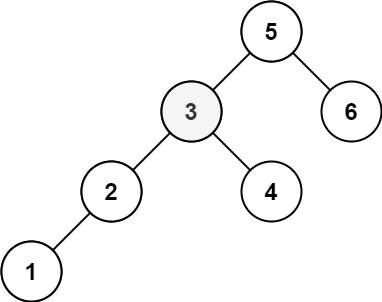
输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3

提示：

• 树中的节点数为 n 。
• 1 <= k <= n <= 10^4
• 0 <= Node.val <= 10^4

4.3解法(中序遍历+计数器剪枝)

算法思路：
我们可以根据中序遍历的过程，只需扫描前k个结点即可。因此，我们可以创建一个全局的计数器count，将其初始化为k，每遍历一个节点就将count--。直到某次递归的时候，count 的值等于 1，说明此时的结点就是我们要找的结果。

算法流程：
1. 定义一个全局的变量count，在主函数中初始化为k的值（不用全局也可以，当成参数传入递归过程中）；

递归函数的设计：int dfs(TreeNode* root):
• 返回值为第k个结点；

递归函数流程(中序遍历):
1. 递归出口：空节点直接返回-1，说明没有找到；
2. 去左子树上查找结果，记为 left：
        a. 如果 left == -1，说明没找到，继续执行下面逻辑；
        b. 如果 left ！= -1，说明找到了，直接返回结果，无需执行下面代码（剪枝）
3. 如果左子树没找到，判断当前结点是否符合：
        a. 如果符合，直接返回结果
4.如果当前结点不符合，去右子树上寻找结果

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int count;int ret = 1;int kthSmallest(TreeNode* root, int k) {count = k;dfs(root);return ret;}void dfs(TreeNode* root){if(root == nullptr||count == 0)return;dfs(root->left);count--;if(count==0)ret = root->val;dfs(root->right);}
};

5.1题目链接：257.二叉树的所有路径

5.2题目描述：

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

示例 1：

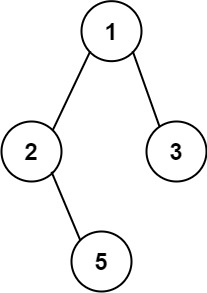
输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

示例 2：

输入：root = [1]
输出：["1"]

提示：

• 树中节点的数目在范围 [1, 100] 内
• -100 <= Node.val <= 100

5.3解法(回溯)：

算法思路：
使用深度优先遍历（DFS）求解。
路径以字符串形式存储，从根节点开始遍历，每次遍历时将当前节点的值加入到路径中，如果该节点为叶子节点，将路径存储到结果中。否则，将"->”加入到路径中并递归遍历该节点的左右子树。
定义一个结果数组，进行递归。递归具体实现方法如下：
        1. 如果当前节点不为空，就将当前节点的值加入路径 path 中，否则直接返回；
        2. 判断当前节点是否为叶子节点，如果是，则将当前路径加入到所有路径的存储数组 paths 中；
        3. 否则，将当前节点值加上“->"作为路径的分隔符，继续递归遍历当前节点的左右子节点。
        4. 返回结果数组。

         特别地，我们可以只使用一个字符串存储每个状态的字符串，在递归回溯的过程中，需要将路径中的当前节点移除，以回到上一个节点。

具体实现方法如下：
1.定义一个结果数组和一个路径数组。
2. 从根节点开始递归，递归函数的参数为当前节点、结果数组和路径数组。
        a. 如果当前节点为空，返回
        b. 将当前节点的值加入到路径数组中。
        c.如果当前节点为叶子节点，将路径数组中的所有元素拼接成字符串，并将该字符串存储到结果数组中。
        d. 递归遍历当前节点的左子树。
        e. 递归遍历当前节点的右子树。
        f.回溯，将路径数组中的最后一个元素移除。以返回到上一个节点

3.返回结果数组

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<string> ret;vector<string> binaryTreePaths(TreeNode* root) {dfs(root,"");return ret;}void dfs(TreeNode* root, string path){path += to_string(root->val);if(root->left == nullptr&&root->right == nullptr){ret.push_back(path);return;}path += "->";if(root->left)dfs(root->left,path);if(root->right)dfs(root->right,path);}
};