【数据结构】排序

目录

1.排序的概念及其运用

1.1排序的概念

1.2常见排序算法

2插入排序

2.1直接插入排序

2.1.1基本思想

2.1.2代码实现

2.1.3特性总结

2.2 希尔排序

2.2.1基本思想

2.2.2代码实现

3.选择排序

3.1选择排序

3.1.1基本思想

3.1.2代码实现

3.1.3特性总结 

3.2 堆排序

4. 交换排序

4.1冒泡排序

4.2快速排序

4.2.1基本思想

4.2.2快排的单趟排序

4.2.3快排的递归实现

4.2.4快排非递归实现

4.2.5时间复杂度分析

5、归并排序

5.1基本思想

5.2代码实现

5.2.1递归实现

5.2.2非递归实现

5.3特性总结

6算法总结

---

1.排序的概念及其运用

1.1排序的概念

排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。

稳定性有意义的场景：

场景1：对一场考试学生成绩的排名，要求相同分数的先交卷的排名较高，这时就要用稳定性好的排序算法

场景2：高考成绩排名，现要求总分相同的学生，按语文成绩高低排名，这时可以先用一个稳定或不稳定的排序算法以语文成绩高低来排序，再用一个稳定的排序算法以总分成绩来排名

内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。

1.2常见排序算法

插入排序：直接插入排序、希尔排序
选择排序：选择排序、堆排序
交换排序：冒泡排序、快速排序
归并排序：归并排序

2插入排序

2.1直接插入排序

2.1.1基本思想

直接插入排序是一种简单的插入排序法,其基本思想是:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列。

实际中我们玩扑克牌时,就用了插入排序的思想

2.1.2代码实现

当插入第 i (i>=1)个元素时,前面的array[0],array[1] ...; array[i-1]已经排好序,将第 i (i>=1) 个元素与array[i-1]、array[i-2]、array[i-3]依次进行比较,找到插入位置,原来位置上的元素顺序后移

以升序为例：

    //将 n 插入一个升序数组，插入后保持有序 int end;//有序数组最后的一个元素的下标 int tmp;//待插入的数据while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];--end;}else{break;}}//退出循环后，有两种情况：1、end == -1 （n 比数组所有元素都要小）//                      2、end 在待插入位置的前一个//                     （两种情况都可以看成end 在待插入位置的前一个）a[end + 1] = tmp;

 如果那个已排好升序的数组初始元素个数只有一个，假定为数组第一个元素，待插入的元素是数组第二个元素，将待插入的元素插入到数组中（其实就是数组第一个元素与第二个元素做比较，然后让它们排升序），这样已排好升序的数组元素个数就有两个了，再将第三个元素作为待插入的元素，按照以上代码那样插入到数组中去，以此类推。

void InsertSort(int* a, int n)
{for(int i = 1; i < n; i++){int end = i - 1; int tmp = a[i];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];--end;}else{break;}}a[end + 1] = tmp;}
}

2.1.3特性总结

直接插入排序的特性总结:
1.元素集合越接近有序,直接插入排序算法的时间效率越高
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1),它是一种稳定的排序算法
4. 稳定性:稳定（如果 tmp > a[end] 或 == a[end]，就 break 了）

2.2 希尔排序

2.2.1基本思想

希尔排序法又称缩小增量法。（shell sort）

希尔排序法的基本思想是:先选定一个整数 n （gap）, 把待排序数组中从第一个元素开始以 n 为间隔分到一个组，然后对该组元素进行直接插入排序。再把从第二个元素开始以 n 为间隔分到一个组，然后对该组元素进行直接插入排序，直到从某个元素开始是已经排过序的了。

（以下例子为排升序）

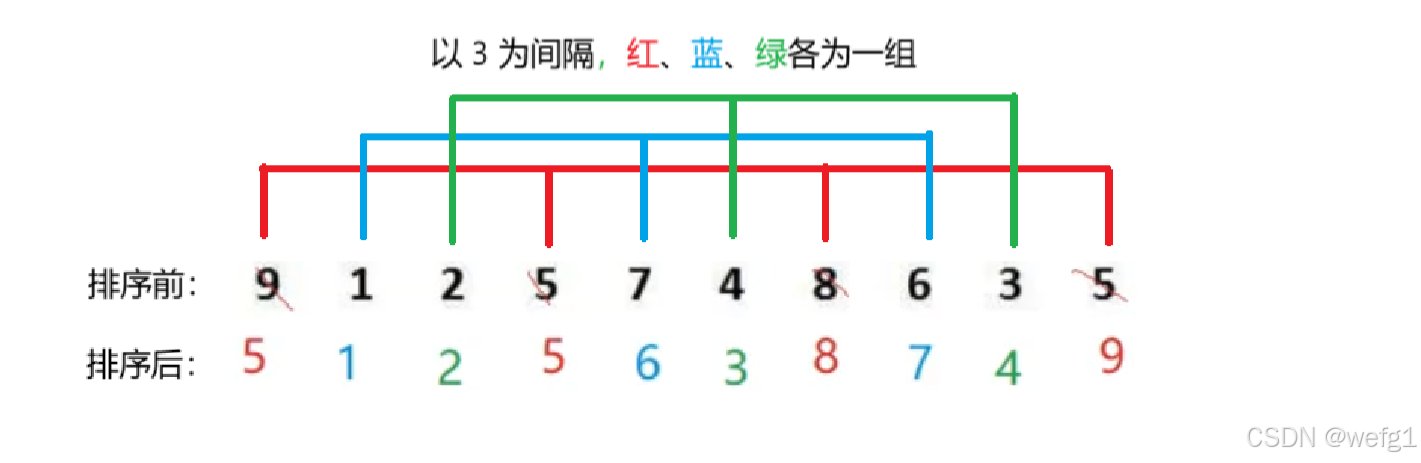
以上过程称为预排序，目的是让大的元素更快到数组的后面，小的元素更快到数组前面，从而让数组接近有序。 （让大的元素更快到数组的后面：如 上面的 9，要到数组的最后，要调换 9 次，而现在只需要调换 3 次）

那么 gap （选定一个整数 n）是多少比较合适呢?

如果 gap == 3，数组 == { 9，8，7，6，5，4，3，2，1，0} 结果：

如果 gap == 5，结果：

可以看出：gap越大 , 跳得越快 , 越不接近有序；gap越小 , 跳得越慢 , 越接近有序

实际上 gap 是一个变化的值，它开始时等于数组的长度，然后每次预排序前都除以 2，直到最后 gap == 1（最后 gap 一定要等于 1 ，任何一个正整数连续除以 2 取商，最后的结果都是 1）

数组 == { 9，1，2，5，7，4，8，6，3，5}，每次预排序后的结果：

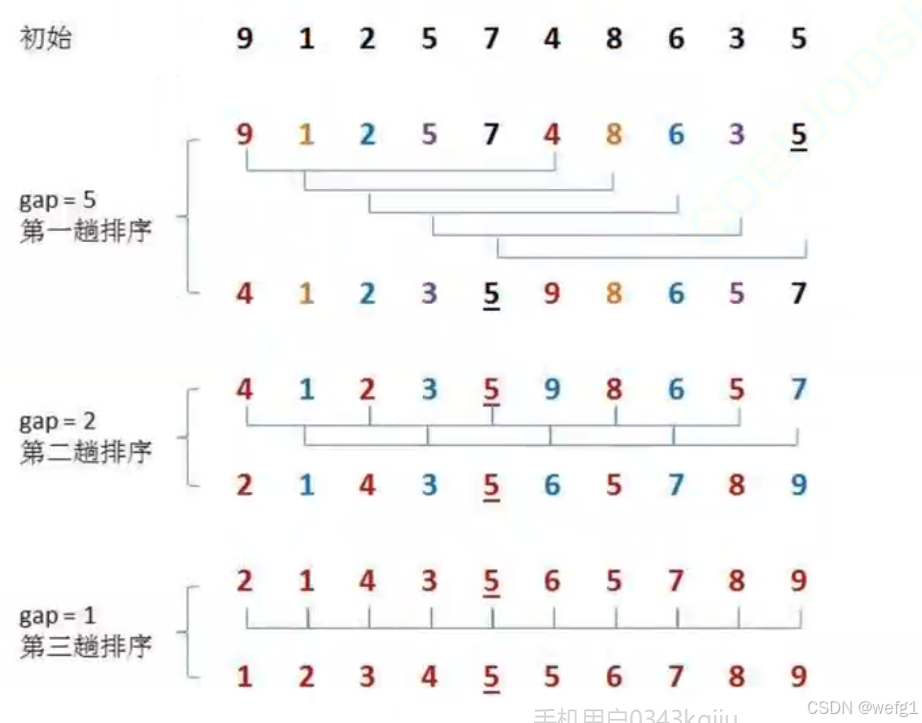
当 gap > 1 时，是预排序，gap == 1 时，是直接插入排序。

希尔排序不稳定，因为大小相同的元素可能会被分到不同的组。

2.2.2代码实现

先实现排好红色组的代码：

for(int i = 0; i < n - gap; i += gap)
{int end = i;int tmp = a[i + gap]; while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end]; end -= gap;}else{break;}}a[end + gap] = tmp;
}

以上代码中的 i 是控制 end 的位置的，可以看出，直接插入排序就是 gap == 1 时的情况，

然后实现排好各组的代码： 

    int gap = 3; for(int j = 0; j < gap; j++){for(int i = 0; i < n - gap; i++){int end = i;int tmp = a[i + gap]; while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end]; end -= gap;}else{break;}}a[end + gap] = tmp;}} 

这种写法是先排好红色组，再排好蓝色组，最后排好绿色组(排好一组，再排另一组），还有一种写法，可以去掉一层循环，这种写法是先排一下红色组，再排一下蓝色组，然后再排一下绿色组，再排一下红色组...（多组并排）。虽然少了一层循环，但是时间复杂度没有发生变化，所以，算时间复杂度不能看有多少层循环。

    int gap = 3; for(int i = 0; i < n - gap; i++){int end = i;int tmp = a[i + gap]; while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end]; end -= gap;}else{break;}}a[end + gap] = tmp;}

最后让 gap 每次预排序前都除以 2，直到最后 gap == 1：

void ShellSort(int* a , int n)
{ int gap = n; while(gap > 1){gap /= 2;for(int i = 0; i < n - gap; i++){int end = i;int tmp = a[i + gap]; while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end]; end -= gap;}else{break;}}a[end + gap] = tmp;}}
}

3.选择排序

3.1选择排序

3.1.1基本思想

每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。

3.1.2代码实现

void SelectSort(int* a, int n)
{int left = 0, right = n - 1;while (left ‹ right){int mini = left, maxi = left; for (int i = left + 1; i <= right; i++){if (a[i] < a[mini]){mini = i;}if (a[i] > a[maxi]){maxi = i;}}Swap(&a[left], &a[mini]); //如果 left 和 maxi 重叠了，交换后需要修正一下if( left == maxi ){maxi = mini}Swap(&a[right], &a[maxi]);++left;--right;}
}

解析：在 left 和 right 之间选出最大值和最小值，然后将最大值和 right 交换，将最小值与 left 交换，然后将 left 向右移动，将 right 向左移动。要小心 left 就是最大值（或 right 就是最小值）的情况，因为如果 left 就是最大值（或 right 就是最小值），将 left 与 mini 交换后，下标 maxi 所表示的元素就不是最大值了。

3.1.3特性总结 

时间复杂度分析：

第一次需要遍历整个数组，遍历的元素的数量为 n，第二次遍历的元素的数量为 n - 2... 所以时间时间复杂度为 O(N^2) ，最好和最坏的情况都是 O(N^2)。 

3.2 堆排序

HeapSort 函数

函数原型：

void HeapSort ( int*a , int n )

a: 待排序的数组的数组名，n：数组元素个数

如果 HeapSort 函数一开始就建立一个堆，然后把数组的所有元素 push 进堆，再 pop 到数组，会有很大的弊端：

1、空间复杂度为O(N)

2、考试时要从头写堆的所有接口，很麻烦

所有我们要使用堆的思想直接对数组排序：

以下是排升序的例子：

先以数组下标为 1 的元素开始，将它作为孩子，然后向上调整，再以下标为 2 的元素向上调整，直到数组最后一个元素，这一步就是在模拟建一个大堆。

然后再根据堆 pop 的思想，模拟堆 pop 的过程，每次 “pop” 出数组最大的元素，将 “pop” 出的元素排在数组倒数第一个位置、倒数第二个位置、倒数第三个位置......，这样，数组就排好升序了。

上文说过，向下调整建堆的方法比向上调整建堆的方法效率更高，所以在该函数中模拟建一个大堆时我们也可以采取向下调整建堆的方法。

注意：

排升序不能建小堆，因为建好小堆之后，最小的元素在根上了，如果把接下来的元素看成一个堆，接下来的元素的关系就全乱了，又要重新建好小堆，其效率还不如每次遍历找最小的元素。

所以，排升序要建大堆：(排降序要建小堆）

建好大堆后，用 pop 的思想将数组的首元素（此时它就是最大的元素）与末尾的元素互换，然后向下调整，向下调整时，将数组元素的个数减一，即将末尾的元素（那个最大的元素）排除在外，因为它已经排好了，向下调整后，数组的首元素就是第二大的元素，以此类推。

堆排序的时间复杂度 

上文已经证明，向下调整建堆的时间复制度是 O(N)，

接下来看看用堆 pop 的思想调整顺序的时间复制度：

排好堆最后一层（数组的后 2 ^（h - 1）个元素）的顺序所需的调整元素的次数为：

2 ^ ( h - 1) * ( h - 1)（堆最后一层一共有 2 ^ ( h - 1) 个结点，每次互换结点后要调整 h - 1 次）

以此类推，设 T(N) 是调整结点位置的总次数，h 是完全二叉树的层数，以最坏的情况来看，

T(N) = 2 ^ 1 * 1 + 2 ^ 2 * 2 + .... + 2 ^ (h-2) * (h-2) + 2 ^ (h-1) * (h-1)

所以，用堆 pop 的思想调整顺序的时间复制度是 O(N * logN)。

所以，不管堆排序中使用向上还是向下调整建堆，时间复制度都是 O(N * logN)。

综上所述，堆排序的时间复杂度是 O(N * logN)

TOP-K问题
即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。

比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

对于Top-Ki问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大（10000亿）,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:

1. 用数据集合中前K个元素来建堆
○ 前k个最大的元素,则建小堆
○ 前k个最小的元素,则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素后向下调整
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。

堆排序不稳定，以下是反例：

4. 交换排序

4.1冒泡排序

void BubbleSort(int* a, int n)
{for (int j = 0; j < n; j++){for (int i = 1; i < n-j; i++){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);}}}
}

先写出单躺的排序（内循环），再写整体的排序（外循环）

判断是否已经有序的优化版本：

void BubbleSort(int* a, int n)
{for (int j = 0; j < n; j++){bool exchage = false;for (int i = 1; i < n-j; i++){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchage = true;}}if(exchage == false){break;}}
}

与直接插入排序的比较

冒泡排序和直接插入排序的时间复杂度最好 (O(N)) 和最坏 (O(N^2)) 都是一样的，为什么直接插入排序比冒泡排序的性能要好呢？

如果数据是有序的，冒泡排序与直接插入排序的效率一样，都是只遍历一遍数组就停止了。如果是接近有序，两者就有一点差距了。如果是部分有序，两者的差距就很大了。

稳定性

如果 a[i - 1] == a[i] ，程序没有做出处理，a[i - 1] 与 a[i] 没有交换，所以是稳定的

4.2快速排序

4.2.1基本思想

快速排序是 Hoare 于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该基准值将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。

如果以基准值（key）成功将区间中数据进行划分，那么这个基准值就已经被放在了它排好序后应出现的位置。

// 假设按照升序对array数组中[left,right)区间中的元素进行排序
void QuickSort(int array[], int left, int right)
{if(right - left <= 1)return;// 按照基准值对array数组的 [left, right)区间中的元素进行划分int div = partion(array, left, right);// 划分成功后以div为边界形成了左右两部分 [left, div)和 [div+1, right) // 递归排[left, div) QuickSort(array, left, div);// 递归排[div+1, right) QuickSort(array, div+1, right);
}

上述为快速排序递归实现的主框架,发现与二叉树前序遍历规则非常像,写递归框架时可想想二叉树前序遍历规则即可快速写出来,后续只需分析如何按照基准值来对区间中数据进行划分的方式即可。

4.2.2快排的单趟排序

将区间按照基准值划分为左右两半部分的常见方式有:

1、霍尔版本

 过程分析：

1、将第一个数组元素作为 key，L 从第一个数组元素出发，R 从最后一个元素出发。

2、R 先出发，一直找到小于或等于 key 的元素后 L 再出发，找到大于或等于 key 的元素。

3、交换 R 和 L 所指示的元素的值

4、重复第 2 步和第 3 步，直到 L 和 R 相遇。

5、将 L 和 R 相遇时所指示的元素和 key 交换。

 注意点：

1、如果是将第一个元素作为 key，那么 R 先出发，找到比 key 小的元素，L 后出发，找到比 key 大的元素；如果是将最后一个元素作为 key，那么 L 先出发，找到比 key 小的元素，R 后出发，找到比 key 大的元素。最后 L 和 R 相遇时指示的元素的值一定比 key 要小。

为什么最后 L 和 R 相遇时指示的元素的值一定比 key 要小呢？

相遇有两种情况:
1、R找到小,L找大没有找到,L遇到R。此时相遇位置的元素显然比 key 要小。
2、R找小,没有找到,遇到L,此时 L 要么经过上一轮交换后是比 key 小的位置，要么没有发生交换 L 还在 key 位置（R 一直找，直接遇到 L）。

2、R 先出发，一直找到小于或等于 key 的元素后 L 再出发，找到大于或等于 key 的元素。R 不能是找严格小于 key 的元素，L 也不能是找严格大于 key 的元素，不然程序可能陷入死循环（L 和 R 都遇到了等于 key 的元素，交换后 L 和 R 所指示的元素仍然等于 key，L 和 R 的位置永远不变了，不能退出循环了）

代码实现：

int keyi = left; 
while (left < right)
{// 右边找小while (left < right && a[right] >= a[keyi])--right;// 左边找大while (left < right && a[left] <= a[keyi])++left;Swap(&a[left], &a[right]);
}Swap(&a[keyi], &a[left]);

代码注意点：

1、在 left 找大和 right 找小的过程中，也要判断 left 是否小于 right ，因为如果数据已经有序，right 可能会发生数组越界。

2、在开始的时候不能让 left 先走一步，因为如果数据已经有序，right 和 left 就会在数组下标为 1 的位置相遇，最后还会将 kay 与 right 和 left 相遇的位置的元素交换。

2、挖坑法

过程分析：

1、 将数组第一个元素存放在 key 变量中，让该位置成为一个坑位。

2、R 往左走，找到比 key 小的元素，将该元素放到坑位去，让该位置成为一个新的坑位。

3、L 往右走，找到比 key 大的元素，将该元素放到坑位去，让该位置成为一个新的坑位。

4、重复第 2 步和第 3 步，直到 L 和 R 相遇。

5、如果 L 和 R 相遇，将 key 放到相遇坑位。

int key = a[left]; 
int hole = left; 
while (left < right)
{// 右边找小while (left < right && a[right] >= key)--right;a[hole] = a[right]; hole = right;// 左边找大while (left < right && a[left] <= key)++left;a[hole] = a[left]; hole = left;
}a[hole] = key;

 注意点：

L 和 R 的相遇位置一定是坑位，因为 L 和 R 相遇时要么 L 是坑位，要么 R 是坑位。 

3、前后指针法

过程分析：

1、开始时 prev 指向 key ，cur 指向 prev 的下一个位置，cur 开始向后走

2、如果cur找到比key小的值,++prev, cur和prev位置的值交换再++cur；

      如果cur找到比key大的值,++cur

3、重复步骤 2 ，直到 cur 越界

4、如果 cur 越界，交换 prev 和 key 的值

说明:
1、prev要么紧跟着cur (prev下一个就是cur)

2、prev要么跟cur中间间隔着比key大的一段数据

代码实现：

    // 三数取中int midi = GetMidNumi(a, left, right);if (midi != left)Swap(&a[midi], &a[left]);int keyi = left;int prev = left; int cur = left + 1; while (cur <= right){if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[cur], &a[prev]);++cur;}Swap(&a[prev], &a[keyi]);return prev;

4.2.3快排的递归实现

1、霍尔版本的递归实现

霍尔版本单趟排序后，将 key 左边的元素和右边的元素又进行单趟排序，即在 key 左边的元素和右边的元素再确定一个 key ，把比 key 小的放在 key 左边，比 key 大的放在 key 的右边...直到 key 左边的元素个数只有一个或为零为止。

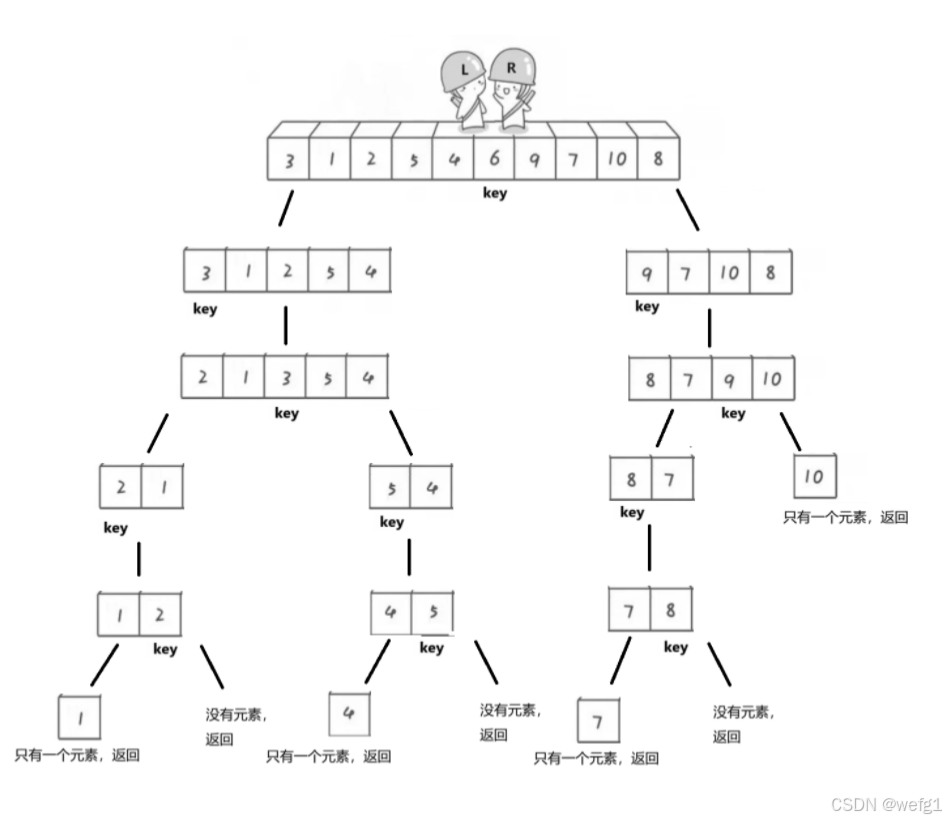
代码实现：

void QuickSort(int* a, int left, int right)
{if (left >= right)return;int begin = left, end = right;int keyi = left; //三数取中或随机选 keywhile (left ‹ right){// 右边找小while (left < right && a[right] >= a[keyi])--right;// 左边找大while (left < right && a[left] <= a[keyi])++left;Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]); keyi = left;// [begin, keyi-1] keyi [keyi+1, end] // 递归QuickSort(a, begin, keyi - 1); QuickSort(a, keyi+1, end);
}

2、挖坑法的递归实现 

void QuickSort(int* a, int left, int right)
{if (left >= right)return;int begin = left, end = right;int key = a[left]; int hole = left; //三数取中或随机选 keywhile (left < right){// 右边找小while (left < right && a[right] >= key)--right;a[hole] = a[right]; hole = right;// 左边找大while (left < right && a[left] <= key)++left;a[hole] = a[left]; hole = left;}a[hole] = key;// [begin, hole-1] hole [hole+1, end] // 递归QuickSort(a, begin, hole - 1); QuickSort(a, hole+1, end);
}

4.2.4快排非递归实现

用栈这种数据结构来非递归实现快排，为什么用栈可以实现快排的非递归呢？观察发现，快排的递归过程类似于二叉树的前序遍历。具体实现细节如下：

1、开始时栈中存放整个数组区间的左右下标

2、栈里面取一段区间,进行单趟排序

3、将单趟排序后的左右子区间入栈

4、重复步骤 2 和 3，如果子区间只有一个值或者不存在就不入栈

5、如果栈为空，结束

代码实现： 

void QuickSortNonR(int* a, int left, int right)
{ST st; StackInit(&st);//将整个数组的左右下标入栈StackPush(&st, right); StackPush(&st, left) ;while (!StackEmpty(&st)){//取出一段区间的左右下标int begin = StackTop(&st); StackPop(&st); int end = StackTop(&st); StackPop(&st);int keyi = PartSort(a, begin, end); // [begin, keyi - 1] keyi [keyi+1, end] if (keyi + 1 < end){StackPush(&st, end); StackPush(&st, keyi+1);}if (begin < keyi - 1){StackPush(&st, keyi); StackPush(&st, begin);}}StackDistroy(&st);
}

代码注意点：

栈中每个结点存储的是一个区间的某个端点，也可以将每个结点变成一个结构体，结构体中存储区间的左右端点，但那样太麻烦了，我们采用每次将两个数据入栈，即左右端点入栈，每次将两个数据出栈，要注意如果先入的左端点后入的右端点，就要先出右端点后出左端点。 

4.2.5时间复杂度分析

最坏的情况，即数组是降序时， 单趟排序后 key 放在了数组的最后，递归时，key 的左边是除 key 外的整个数组，key 的右边没有元素，也就是说，每次递归时待排序的元素个数都减 1，那么递归的次数就是数组元素个数（个数太多会栈溢出），每次递归都要遍历 n - 1、n - 2、n - 3 ... 个元素，此时的时间复杂度就是 O(N^2) 。

当数组本身就是升序时，时间复杂度也是 O(N^2)。

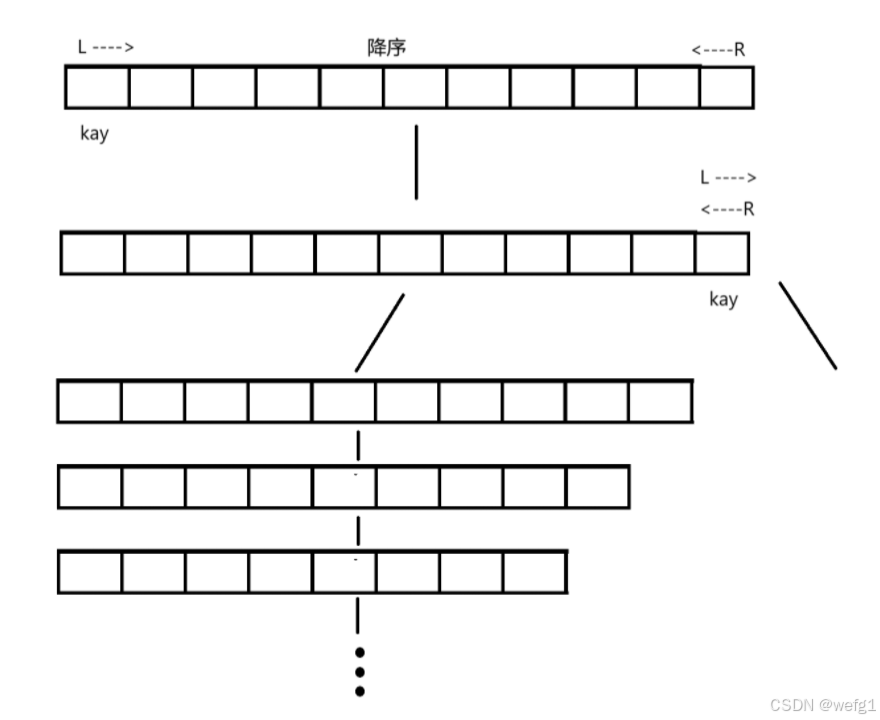
所以快排的效率快慢关键在于 key 被调换后的位置是否在数组偏中间的位置，因为如果在数组偏中间的位置，那么 key 左右就分得均匀，递归的层数就越少，遍历数组的次数就越少（每层递归都大概要遍历一次数组）。

如果 key 被调换后的位置在数组偏中间的位置，那么 key 左右就分得均匀，此时快排的递归层数是 log(N - 1)，N 是数组元素个数，每层递归都要遍历一次数组，所以时间复杂度是 O(N*logN)

那么如何使 key 被调换后的位置在数组偏中间的位置，使 key 左右的元素个数相近呢？

1、随机选 key

让 key 的选择变得随机而不是默认是第一个元素。

int randi = left + (rand() % (right - left)); 
Swap(&a[left], &a[randi]) ;

把 a[randi] 和 a[left] 位置互换的目的是使随机选择的 key 位置在最左边

2、三数取中

在待排序的区间中，选择首元素、最后一个元素或中间的元素中既不是最大也不是最小的元素。

void GetMidNumi(int* a, int left, int right)
{int mid = (left + right) / 2; if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]){return left;}else{return right;}}else // a[left] > a[mid]{if (a[mid] > a[right]){return mid;}else if (a[left] < a[right]){return left;}else{return right;}}
}

// 三数取中
int midi = GetMidNumi(a, left, right); 
if(midi != left)Swap(&a[midi], &a[left]);

三数取中的优化比随机选 key 的优化更好 

 除了对选 key 进行优化以减少递归层数外，还可以对递归过程进行优化：

如果待排序的区间数据量已经很少，此时如果继续使用递归，会显得很麻烦，因为即使数据量已经很少，却递归调用了很多次函数。所以我们可以在待排序的区间数据量已经很少时，采用直接插入排序方法让该区间有序。

void QuickSort(int* a, int left, int right)
{if (left >= right)return;// 小区间优化 -- 小区间使用直接插入排序if ((right - left + 1) > 10){int keyi = PartSort(a, left, right); //PartSort 是单趟排序QuickSort(a, left, keyi - 1); QuickSort(a, keyi + 1, right);}else{InsertSort(a + left, right - left + 1);}
}

5、归并排序

5.1基本思想

归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。归并排序核心步骤:

 

5.2代码实现

5.2.1递归实现

要创建一个临时数组，来存储合并后的结果，再将临时数组的内容拷贝到原数组

void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n); if (tmp == NULL){perror("malloc fail\n");return;}_MergeSort(a, 0, n - 1, tmp);free(tmp);
}

为了实现递归，MergeSort 函数不能调用自己，不然每次递归都要创建数组。所以我们新命名一个函数 _MergeSort ，在这个函数中实现递归。

void _MergeSort(int* a, int begin, int end, int* tmp)
{if(begin >= end)reurn;int mid = (begin + end) / 2; // [begin, mid] [mid+1,end], 子区间递归排序_MergeSort(a, begin, mid, tmp); _MergeSort(a, mid+1, end, tmp);// [begin, mid] [mid+1,end]归并int begin1 = begin, end1 = mid; int begin2 = mid+1, end2 = end; int i = begin; while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++]}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}

 代码注意点：

1、while 循环的条件是循环继续的条件而不是循环结束的条件，所以 while (begin1 <= end1 && begin2 <= end2) 中 && 不能写成 || 。只要有一个子区间全部归并到了 tmp ，就结束循环，由下面的代码判断是哪个子区间还有元素没有归并。

2、归并时如果两个数相等，就把 a[begin1] 放在 tmp 数组，这样可以保证稳定性。 

5.2.2非递归实现

为什么归并排序的非递归不能像快排那样使用栈这种数据结构呢？原因在于归并排序的过程类似于二叉树的后序遍历，而快排的过程类似于前序遍历。

可以跳过分割的过程，直接对数组进行归并：开始时一 一归并，然后二二归并... 如下图所示：

void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n); if (tmp == NULL){perror("malloc fail\n"); return;}int gap = 1; while( gap < n ){for (int i = 0; i < n; i += 2 * gap){//[begin1,end1] 和 [begin2,end2] 归并int begin1 = i, end1 = i + gap - 1; int begin2 = i + gap, end2 = i + 2 * gap - 1; if(end1 >= n || begin2 >= n){break;}if(end2 >= n){end2 = n - 1;}int j = i; while(begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while(begin1 <= end1){tmp[i++] = a[begin1++];}while(begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;}free(tmp);
}

代码注意点：

1、gap 是归并时每组的元素个数，刚开始是 1（两个元素归并成一组），然后是 2（两个元素和两个元素归并成一组），循环每走一次，表示归并一组，所以 i 每次都 += 2 * gap。 

2、begin1 是不可能越界的，因为 begin1 就是 i，循环的条件是 i < n; end1、begin2、end2 可能越界

 end1 越界：

end1 越界了，begin2 和 end2 肯定都越界了，不需要进行归并了，但 [ begin1 , end1] 仍要拷贝到 tmp 再拷贝回原数组，否则 tmp 对应原数组位置的地方可能不是与原数组一样的值。

（最好不要将 tmp 一次性全部拷贝到原数组，而是归并一组后拷贝一次，这样会简化代码）

这种情况如何修正呢？

直接退出循环

end1 没有越界，begin2 越界：

begin2 就在 end1 的后面，如果 begin2 越界，处理方式可以与 end1 越界一样。 

end1 、begin2没有越界，end2 越界：

这种情况较好处理：修正 end2 = n - 1；然后继续归并

5.3特性总结

1. 归并的缺点在于需要O(N)的空间复杂度,归并排序更多是解决在磁盘中的外排序问题。
2. 时间复杂度:O(N*logN)
3. 空间复杂度: O(N)
4. 稳定性:稳定

6算法总结