当前位置：首页 > news >正文

动态规划dp专题-（上）

news 来源：原创 2025/9/21 4:51:23

dp理论知识🔥🔥

🎯一、线性DP

（1）🚀斐波那契数 -入门级

（2）🚀898. 数字三角形-acwing ---入门级

（3）往期题目

①选数异或：在 [l, r] 区间是否能找到 a[i] ^ a[j] = x 的数对？

②🚀破损的楼梯：

③🚀安全序列：

🎯二、背包问题 ✅✅✅【很重要！！】

（1） 494. 目标和 - 力扣 --(0-1背包) 【给定背包容量，装满背包有多少种方法】

🤯🤯🤯🤯🤯🤯🤯🤯🤯

（2）322. 零钱兑换 - 力扣（完全背包）--

（3）518. 零钱兑换 II - 力扣（完全背包）-和25-3-2的csp题基本一样

（4）377. 组合总和 Ⅳ - 力扣（LeetCode） --完全背包

（5）57. 爬楼梯（卡玛）

🤯🤯🤯🤯🤯🤯🤯🤯🤯

（6）46. 携带研究材料（0-1背包）【给定背包容量装满背包的最大价值是多少】

（7）最快洗车时间（0-1）背包

（8）474. 一和零 - 力扣（0-1背包）【给定背包容量，装满背包最多有多少个物品】

（9）279. 完全平方数 -（完全背包）

🎯三、子序列LSCDP 【线性DP的一个分支】

（1）895. 最长上升子序列 - AcWing题库

（2）674. 最长连续递增序列 - 力扣（LeetCode）

（3）最长公共子序列 - acwing

（4）1035. 不相交的线 - 力扣

（5）718. 最长重复子数组 - （最长连续公共子序列）

（6）53. 最大子数组和 - 力扣

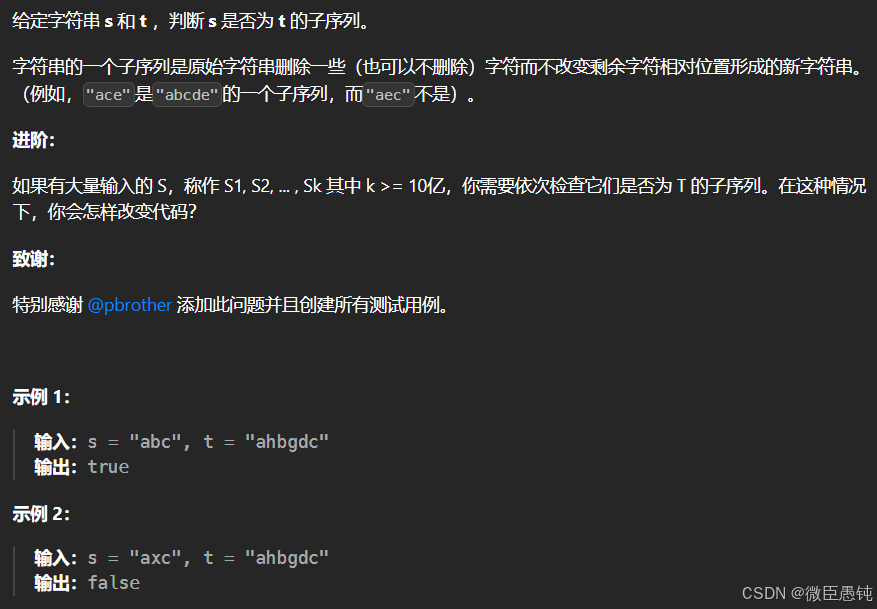
（7） 392. 判断子序列 - 力扣

（8）拍照【最长山峰子序列】---已发博客，点击标题跳转

（9）72. 编辑距离 - 力扣

dp理论知识🔥🔥

很多讲解动态规划的文章都会讲最优子结构啊和重叠子问题啊这些，这些东西都是教科书的上定义，晦涩难懂而且不实用。家知道动规是由前一个状态推导出来的对于刷题来说就够用的。

通常用于求解最值问题（最大值、最小值、最短路径等）或计数问题（方案总数等），一般看到题目中有"最大/最小"、"最多/最少"、"最长/最短"、"最高/最低、"有多少种方法"、"可能的方案数"、"不同方式的数量"等可以考虑是否用dp。

动态规划，一般分为5个步骤：

①确定dp数组以及下标的含义

就是 dp[i] 这个值，是什么意思？以i为结尾，如何如何；或者以i为起点，如何如何。

🌰dp[i][j] 表示 A 的前 i 个字符和 B 的前 j 个字符的最长公共子序列

dp[i][j] 表示二维网格中从 (0,0) 到 (i,j) 的最短路径

dp[i][j] 表示考虑前 i 件物品，背包容量为 j 时的最大价值

dp[i] 表示以 nums[i] 结尾的最长递增子序列长度

②确定递推公式【状态转移方程】（核心）

状态转移方程就是：dp[i] 等于什么 ？【我的经验是多做题，一般都是模版题或者模版题的变形】

状态转移方程，就是根据 dp[ i ] 之前或者 dp[ i ] 之后，来推导出 dp[ i ] 的值
只要你能根据之前或或者之后的值来推导出 dp[ i ] 的值，那么，状态转移方程就出来了
但是，怎么推？
这个就要就题目而言，大体的思路是这样的：根据最近的状态来划分问题
一般来说，dp[i] 的值，要么是前面的 dp[i-1] 或者后面的 dp[i+1]，一定要十分明确dp数组的含义

③dp数组如何初始化

初始化就是保证，在我们进行填表的时候不越界，dp[0]、dp[1] 是多少？
例如说，我要求 dp[0] / dp[1] 的值，需要前面的位置，但是此时明显已经越界
因此，这两个位置需要单独处理

④确定遍历（填表）顺序：从前往后还是从后往前？

什么是填表顺序？

如i位置值得求解，需要前面两个位置的值已经存在才能求解
因此，也就是说在算i位置时，i-1 和 i-2 位置已经填了，已经有值了
所以，我们的填表顺序应该是从前往后，因为后面的值的求解需要前面的值
反之，就是从后往前。

⑤举例推导dp数组

代入具体数值，检查推导是否正确

动态规划应该如何debug？ 找问题的最好方式就是把dp数组打印出来，看看究竟是不是按照自己思路推导的！

如果代码写出来了，一直AC不了，灵魂三问：

这道题目我举例推导状态转移公式了么？
我打印dp数组的日志了么？
打印出来了dp数组和我想的一样么？

🎯一、线性DP

emm 比较基础的DP问题，挺简单的-求解具有线性结构的最优子问题

线性DP指问题的状态转移沿单一维度展开，通常表现为：

状态定义在一维数组或线性序列（如字符串、数组）上
状态转移方程仅依赖前序有限个状态

dp[i]：以第i个元素结尾的最优解 dp[i]：前i个元素构成的子问题的解

（1）🚀斐波那契数 -入门级

https://leetcode.cn/problems/fibonacci-number/description/

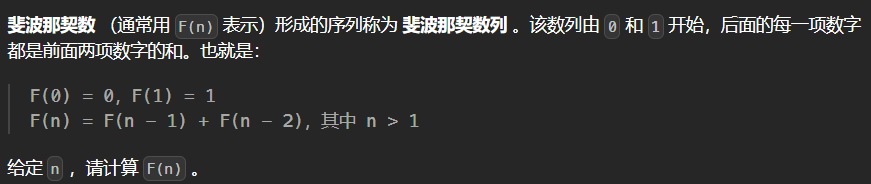509. 斐波那契数 - 力扣（LeetCode） ----写的超好的一篇题解！！！最有收获的一段话：

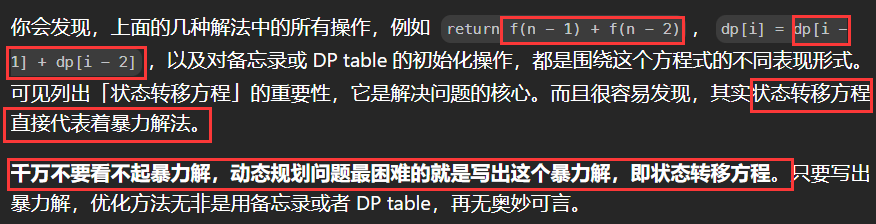
① dp[i]的定义为：第i个数的斐波那契数值是dp[i]

②题目已经把递推公式直接给我们了：状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];

③dp数组如何初始化：dp[0]=0,dp[1]=1;

④确定遍历顺序：从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出，dp[i]是依赖 dp[i - 1] 和 dp[i - 2]，那么遍历的顺序一定是从前到后遍历的

⑤举例推导：

按照这个递推公式dp[i] = dp[i - 1] + dp[i - 2]，我们来推导一下，当N为10的时候，dp数组应该是如下的数列：

0 1 1 2 3 5 8 13 21 34 55

如果代码写出来，发现结果不对，就把dp数组打印出来看看和我们推导的数列是不是一致的。

class Solution {
public:int fib(int N) {if (N <= 1) return N;vector<int> dp(N + 1);dp[0] = 0;dp[1] = 1;for (int i = 2; i <= N; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[N];}
};

当然可以发现，我们只需要维护两个数值就可以了，不需要记录整个序列：将空间复杂度由n将为1

class Solution {
public:int fib(int N) {if (N <= 1) return N;int dp[2];dp[0] = 0;dp[1] = 1;for (int i = 2; i <= N; i++) {int sum = dp[0] + dp[1];dp[0] = dp[1];dp[1] = sum;}return dp[1];}
};

（2）🚀898. 数字三角形-acwing ---入门级

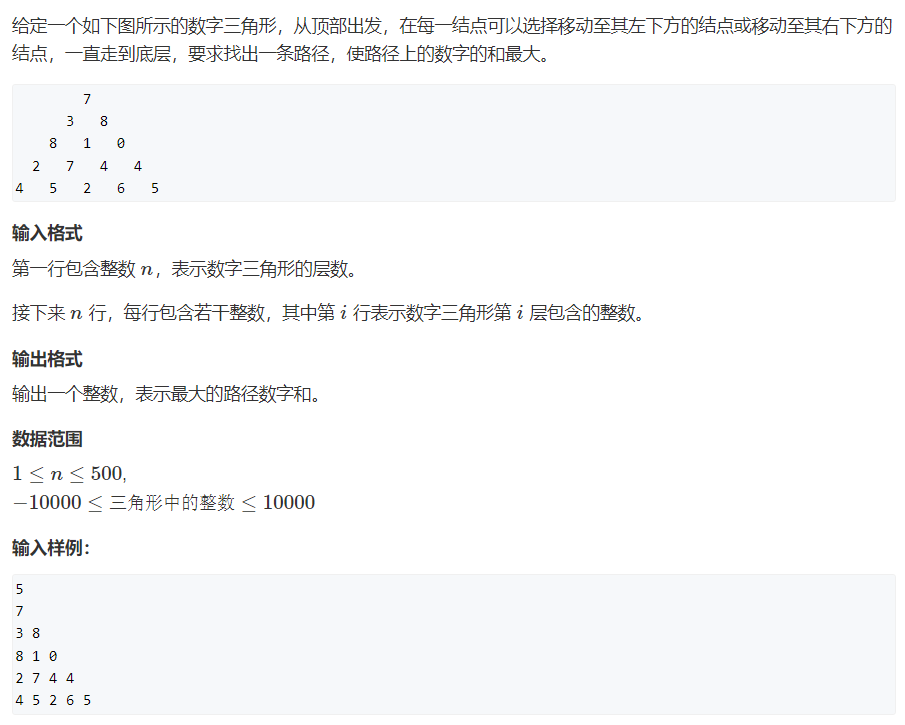
如何确定状态转移方程呢？因为每个位置只能由上一层的相邻位置到达，也就是对于第i行第j列的位置，它只能从第i-1行的第j-1列或者第j列的位置下来（假设每行是从左到右编号的）。所以，状态转移方程应该是dp[i][j] = max(dp[i-1][j-1], dp[i-1][j]) + a[i][j]，其中a[i][j]是三角形中第i行第j列的数字。

#include<bits/stdc++.h>
using namespace std;
const int N=510;
int dp[N][N]; //dp[i][j]:到达第i行第j列的位置时，所能获得的最大路径和
int a[N][N];//三角形
int n;
int main(){cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){cin>>a[i][j];}}//初始化memset(dp, -0x3f3f3f3f, sizeof dp); dp[1][1]=a[1][1];//dpfor(int i=2;i<=n;i++){for(int j=1;j<=i;j++){//转移方程dp[i][j]=max(dp[i-1][j-1],dp[i-1][j])+a[i][j];}}int res=INT_MIN;//最后一行找最大的for(int i=1;i<=n;i++){res=max(res,dp[n][i]);}cout<<res;return 0;
}

（3）往期题目

【AcWing】动态规划-线性DP -选数异或-CSDN博客

【蓝桥】线性DP-破损的楼梯-CSDN博客

【蓝桥】线性DP-安全序列-CSDN博客

回顾了一下这几道题目，简单总结下吧~

①选数异或：在 `[l, r]` 区间是否能找到 `a[i] ^ a[j] = x` 的数对？

dp[i] ：在前 i 个元素中，能够与第 i 个元素构成异或为 x 的元素的最左位置

dp[i] = max(dp[i - 1], last[x ^ a])

这道题思维很奇特！！我真的想不到可以如此定义dp数组，第一遍看题解理解了好久，这次再回顾的时候一下就顿悟了哈哈哈，真的很有趣的一道题，不过我自己真的想不到这样的dp定义.......（题还是做少了吧·······）

②🚀破损的楼梯：

看到这道题目第一眼，很明显就是用dp解决（求方案数）

dp[i]:到第i级台阶的方案数

dp[i] = dp[i-1] +dp[i-2]

dp数组的定义和转移方程都不难想到，其实就是斐波那契数列。，但是题目多了一个特殊条件（有破损的楼梯），（分情况！！）这里可以学到遇到破损的（障碍）时候应该如何应对，即让其dp[i] =0 ,到达破损楼梯的方案数为0,注意初始化 dp[0] = 1

③🚀安全序列：

类似“在长度为 n 的位置中，按照一定规则放置物品（如桶）”的问题。(求方案数）

需要分情况！！

我自己写的时候dp[i] 的含义很好猜前i个位置已经安放好的方案总数，然后我反推状态方程，也分了第 i 空位可以放桶和不可以放两种情况，还是很简单的一道题dp[i]=(dp[i-1]+1) 【不放】 当第i位放时，要求第i-k那不能放，此时dp[i]=dp[i-1] + dp[i-k-1]

注意初始化dp[0]=1(就是全空一种情况)

🎯二、背包问题 ✅✅✅【很重要！！】

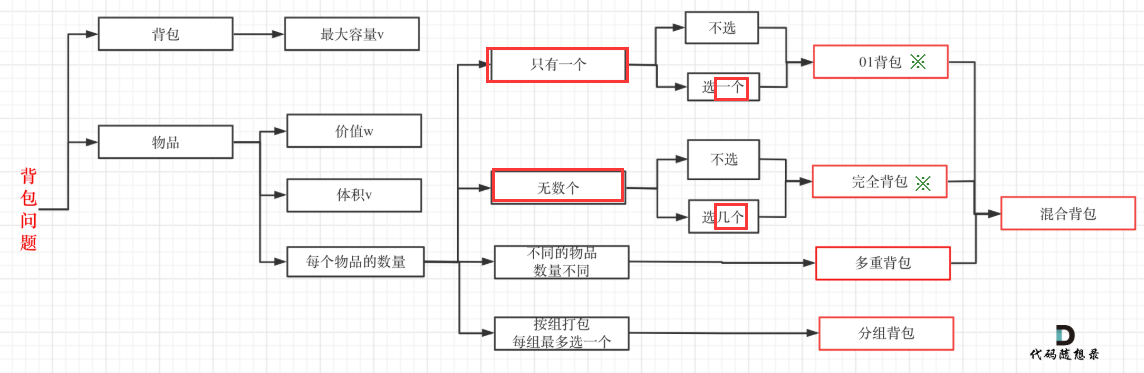
【Acwing】背包问题汇总--理解DP动态规划-CSDN博客 ---之前总结的背包的原始题目很详细了（yxc版本）我在原文章进一步优化了一下，直接看原文章的背包问题汇总叭~~~

下面几个是背包问题的应用，都是用的背包问题的模版（包括2025/3月份csp考试的第二题【与100分失之交臂！！！！啊啊】）

（1） 494. 目标和 - 力扣 --(0-1背包) 【给定背包容量，装满背包有多少种方法】

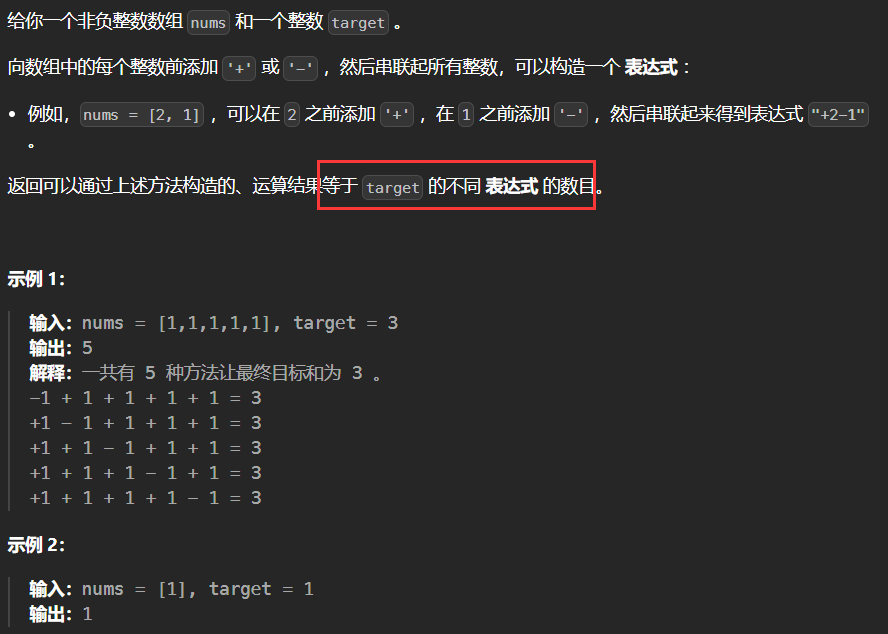
emmm有点难度但是很有趣哇，不是简单套末班就可以AC的，每个数可以选择加或者减，那么总和的话，可以看成是把这些数分成两个子集，一个是正数的和，一个是负数的和的绝对值。假设正数的和是S，负数的和是total_sum - S。那么总的效果就是S - (total_sum - S) = target。也就是2S = target + total_sum。所以，我们需要找到有多少个子集，使得它们的和等于(target + total_sum)/2。 此时问题就转化为，用nums装满容量为(target + total_sum)/2的背包，有几种方法。

然后套0-1背包问题的模版就好啦~~注意return 0 的两种情况

class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {// 计算数组的总和int sum = accumulate(nums.begin(), nums.end(), 0);// 如果 |target| > sum，说明不可能找到符合条件的子集，返回 0// 如果 (sum + target) 不是偶数，说明无法拆分成两个整数子集，返回 0if (abs(target) > sum || (sum + target) % 2 != 0) return 0;// 计算子集和 s，使得 P - N = target，且 P + N = sum// 解得 P = (sum + target) / 2，即找到一个子集 P 使其和为 sint s = (sum + target) / 2;// 定义 dp 数组，dp[j] 表示能够凑成 j 的方案数vector<int> dp(s + 1, 0);dp[0] = 1; // 只有一种方法能凑成 0，即什么都不选// 遍历每个数for (int num : nums) {// 逆序遍历 dp 数组，确保每个 num 只被使用一次（避免重复选择）for (int j = s; j >= num; j--) {// 状态转移：dp[j] 表示选择 num 之后的方案数dp[j] += dp[j - num];}}// 返回凑成 s 的方案数return dp[s];}
};

🤯🤯🤯🤯🤯🤯🤯🤯🤯

（2）322. 零钱兑换 - 力扣（完全背包）--

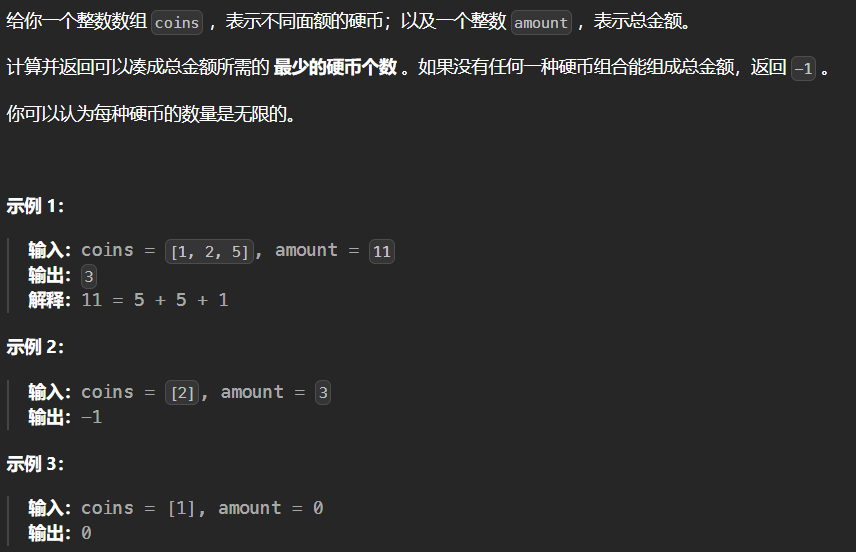
class Solution {
public:int coinChange(vector<int>& coins, int amount) {//dp[i][j]:前i个coins凑成金额为j的最小硬币个数vector<vector<unsigned long long>> dp(coins.size(),vector<unsigned long long>(amount+1,INT_MAX ));for (int i = 0; i < coins.size(); i++) {dp[i][0] = 0;}// 处理第一种硬币的情况for (int j = coins[0]; j <= amount; j++) {if (j % coins[0] == 0) {dp[0][j] = j / coins[0];}}//dpfor(int i=1;i<coins.size();i++){for(int j=1;j<=amount;j++){if(coins[i]>j) dp[i][j]=dp[i-1][j];else{dp[i][j]=min(dp[i-1][j],dp[i][j-coins[i]]+1);}}}return (dp[coins.size()-1][amount]==INT_MAX)? -1:dp[coins.size()-1][amount];        }
};

dp 的第二维大小必须是 amount + 1，以便包含所有可能的金额从 0 到 amount

滚动数组优化~：

class Solution {
public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount+1,INT_MAX-1);//避免 INT_MAX + 1 溢出dp[0]=0;// 金额 0 需要 0 枚硬币//dpfor(int i=0;i<coins.size();i++){for(int j=coins[i];j<=amount;j++){dp[j]=min(dp[j],dp[j-coins[i]]+1);}}return dp[amount]==INT_MAX-1?-1:dp[amount];}};

（3）518. 零钱兑换 II - 力扣（完全背包）-和25-3-2的csp题基本一样

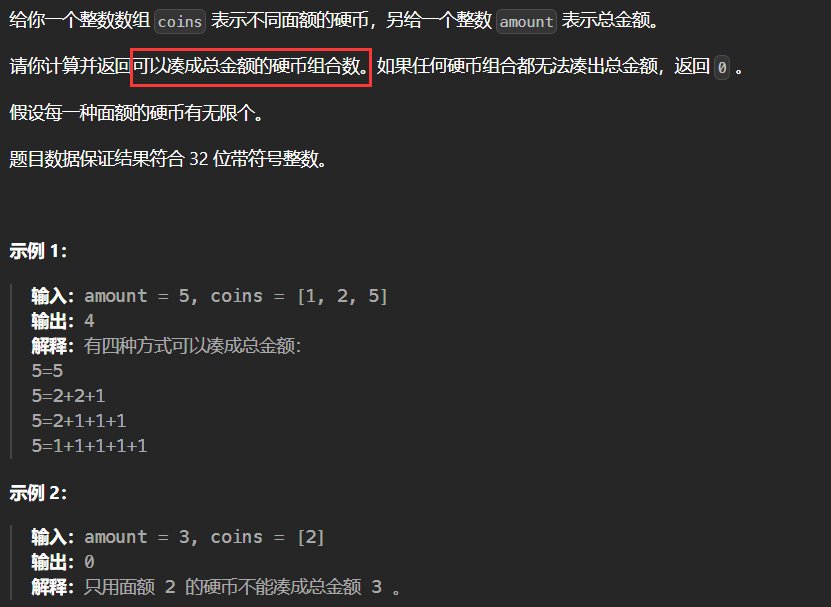
类似这种题目：给出一个总数，一些物品，问能否凑成这个总数。（1--3题都是这样的）

这是典型的背包问题！但本题和纯完全背包不一样，纯完全背包是凑成背包最大价值是多少，而本题是要求凑成总金额的物品组合个数！

因为每一种面额的硬币有无限个，所以这是完全背包（laoz当时咋就没想到，，）

这里注意初始化问题：

当金额为0时，无论使用多少种硬币，只有一种组合方式，即不选择任何硬币，因此所有的dp[i][0] = 1；
对于第一种硬币（i=0），只有当金额是其倍数时，组合数为1，否则为0。
dp[0][j] = (j % coins[0] == 0) ? 1 : 0
遍历顺序：

因为纯完全背包求得装满背包的最大价值是多少，和凑成总和的元素有没有顺序没关系，即：有顺序也行，没有顺序也行！

而本题要求凑成总和的组合数，元素之间明确要求没有顺序。所以纯完全背包是能凑成总和就行，不用管怎么凑的。

【本题是求组合数，所以先遍历物品再遍历背包容量】

然后就是完全背包的模版啦（注意开unsigend long long）

class Solution {
public:int change(int amount, vector<int>& coins) {// dp[i][j]：从前i个coin中选能够凑满j（包括j）这么大容量的包，有dp[i][j]种组合方法。vector<vector<int>> dp(coins.size(),vector<int>(amount+1,0));// 初始化：金额为0时组合数为1for (int i = 0; i < coins.size(); ++i) {dp[i][0] = 1;}// 处理第一种硬币的情况for (int j = 1; j <= amount; ++j) {dp[0][j] = (j % coins[0] == 0) ? 1 : 0;}//dpfor(int i=1;i<coins.size();i++)//遍历物品{for(int j=1;j<=amount;j++)//遍历容量{if(coins[i]>j) dp[i][j]=dp[i-1][j];else dp[i][j]=dp[i-1][j]+dp[i][j-coins[i]];}}return dp[coins.size()-1][amount];}
};

数组开小了~~

滚动数组优化+扩宽存储范围：

class Solution {
public:int change(int amount, vector<int>& coins) {vector<unsigned long long> dp(amount+1,0);dp[0]=1;//dpfor(int i=0;i<coins.size();i++){for(int j=coins[i];j<=amount;j++){dp[j]=dp[j]+dp[j-coins[i]];}}return dp[amount];}};

（4）377. 组合总和 Ⅳ - 力扣（LeetCode） --完全背包

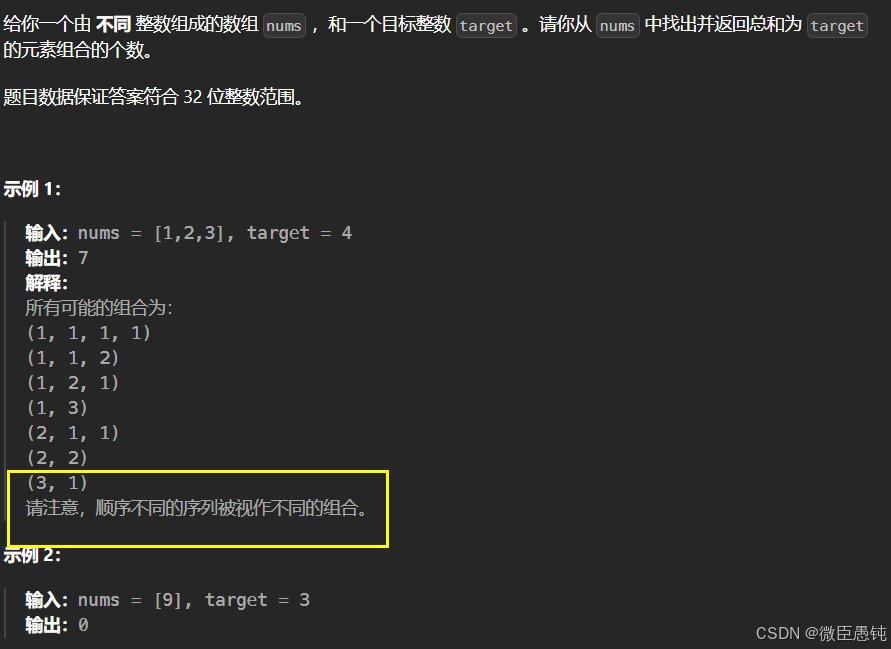
（2）要求最少硬币数量，要求硬币是组合数还是排列数都无所谓！所以两个for循环先后顺序怎样都可以！ (3）是求硬币凑出来的方案个数，每个方案个数是组合数，所以必须外层for循环遍历物品，内层for遍历背包；而（4）本题目描述说是求组合，但又说是可以元素相同顺序不同的组合算两个组合，其实就是求排列！（直接记住滚动数组优化后的模版！！！）

class Solution {
public:int combinationSum4(vector<int>& nums, int target) {// dp[j] 表示组成和为j的排列总数vector<int> dp(target + 1, 0);// 初始化：和为0的排列只有1种（空集）dp[0] = 1;// 外层循环遍历所有可能的目标和（背包容量）for (int j = 0; j <= target; j++) { // 内层循环遍历所有数字（物品）for (int i = 0; i < nums.size(); i++) { // 当目标和>=当前数字时，可以进行状态转移if (j >= nums[i]) {/* 状态转移方程：当前和为j的排列数 = 已计算的排列数 + 使用当前数字前的排列数（j - nums[i]时的排列数）例如：当nums[i]=2，j=5时dp[5] += dp[3] 表示所有和为3的排列末尾加上2的情况这体现了排列顺序不同视为独立解的特性*/dp[j] += dp[j - nums[i]];}}}return dp[target];}
};

有两个测试用例相加超过Int的范围，所以开大一点：

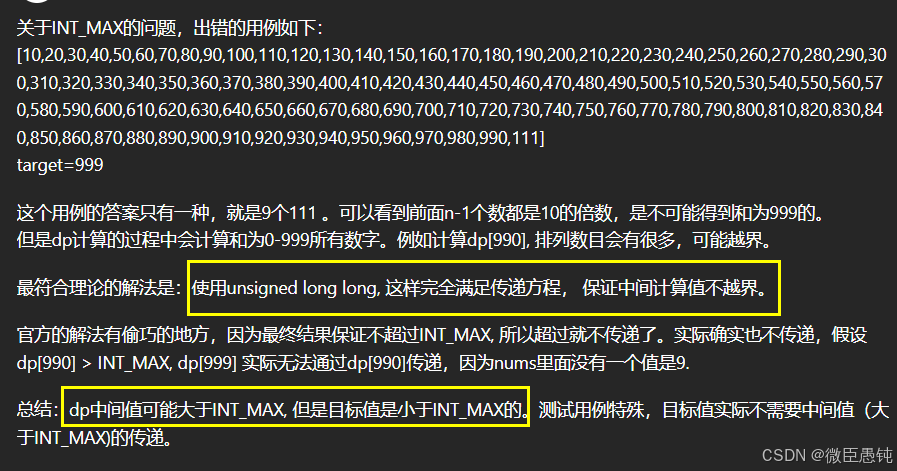
class Solution {
public:int combinationSum4(vector<int>& nums, int target) {// dp[j] 表示组成和为j的排列总数vector<unsigned long long> dp(target + 1, 0);// 初始化：和为0的排列只有1种（空集）dp[0] = 1;// 外层循环遍历所有可能的目标和（背包容量）for (int j = 0; j <= target; j++) { // 内层循环遍历所有数字（物品）for (int i = 0; i < nums.size(); i++) { // 当目标和>=当前数字时，可以进行状态转移if (j >= nums[i]) {/* 状态转移方程：当前和为j的排列数 = 已计算的排列数 + 使用当前数字前的排列数（j - nums[i]时的排列数）例如：当nums[i]=2，j=5时dp[5] += dp[3] 表示所有和为3的排列末尾加上2的情况这体现了排列顺序不同视为独立解的特性*/dp[j] += dp[j - nums[i]];}}}return dp[target];}
};

（5）57. 爬楼梯（卡玛）

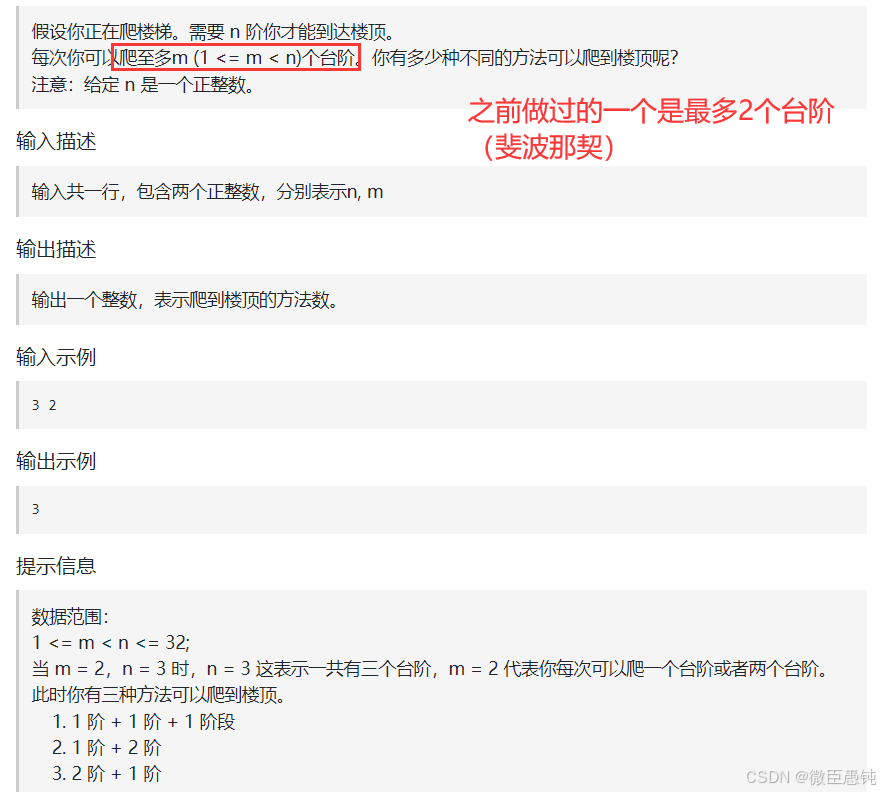
很明显是求排列数，允许顺序不同~~直接套末班

一遍AC~~~开心

#include<bits/stdc++.h>
using namespace std;
const int N=35;
int dp[N];
int n,m;
int main()
{cin>>n>>m;//m为物品 n为背包容量dp[0]=1;for(int j=1;j<=n;j++){for(int i=1;i<=m;i++){dp[j]+=dp[j-i];}}cout<<dp[n];return 0;
}

🤯🤯🤯🤯🤯🤯🤯🤯🤯

（6）46. 携带研究材料（0-1背包）【给定背包容量装满背包的最大价值是多少】

//纯模版 和0-1背包没什么不同ok?
#include<bits/stdc++.h>
using namespace std;
const int N=5010;
int dp[N][N];
int weight[N],value[N];
int main()
{int m,n;cin>>m>>n;//输入所占空间for(int i=1;i<=m;i++) cin>>weight[i];for(int i=1;i<=m;i++) cin>>value[i];//dpfor(int i=1;i<=m;i++){for(int j=0;j<=n;j++){if(weight[i]>j) dp[i][j]=dp[i-1][j];elsedp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);}}cout<<dp[m][n];return 0;
}

（7）最快洗车时间（0-1）背包

已发bolg

        基于 0/1 背包思想 解决洗车时间分配问题，不是完全的模版题，本质上是子集和问题【给定一个正整数数组 nums 和一个目标值 target，判断是否可以从 nums 选择若干个数（每个数最多选一次），使其和恰好等于 target】每辆车的洗车时间类似于 物品的重量

dp[i][j] 表示前 i 辆车是否可以凑出洗车时间 j

不选当前车：dp[i][j] = dp[i-1][j]

选当前车（当前车时间 car[i]）：dp[i][j] |= dp[i-1][j - car[i]]（如果没有|会丢失一种情况，不能直接等于）

（一维：  dp[j] 能否恰好放入总时间不超过 j 的任务,滚动数组优化，注意逆序遍历）

（8）474. 一和零 - 力扣（0-1背包）【给定背包容量，装满背包最多有多少个物品】

这题也有点难度，这个背包有两个维度，一个是m 一个是n，而不同长度的字符串就是不同大小的待装物品

本题中strs 数组里的元素就是物品，每个物品都是一个！这就是一个典型的01背包！ 只不过物品的重量有了两个维度而已。

dp[i][j]：最多有i个0和j个1的strs的最大子集的大小为dp[i][j]

dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1)

知道这些代码就很好写啦【因为背包已经有两个维度了，所以我们直接使用滚动数组的模版，否则要建三维数组！！】

class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {// 初始化dp数组，dp[i][j] 表示在最多有 i 个 '0' 和 j 个 '1' 的情况下，能够组成的最大子集大小vector<vector<int>> dp(m+1, vector<int>(n+1, 0));// 遍历每个字符串（物品）for(string str : strs) { int one_num = 0, zero_num = 0;// 统计当前字符串中的 '0' 和 '1' 的数量for(char c : str) {if(c == '0') zero_num++;else one_num++;}// 采用 **逆序遍历**，确保每个字符串只能被选择一次（类似 0/1 背包问题）for(int i = m; i >= zero_num; i--) { // 遍历 '0' 的背包容量for(int j = n; j >= one_num; j--) { // 遍历 '1' 的背包容量// 状态转移：当前选择该字符串后，取最大值dp[i][j] = max(dp[i][j], dp[i - zero_num][j - one_num] + 1);}}}// 返回能组成的最大子集大小return dp[m][n];}
};

（9）279. 完全平方数 -（完全背包）

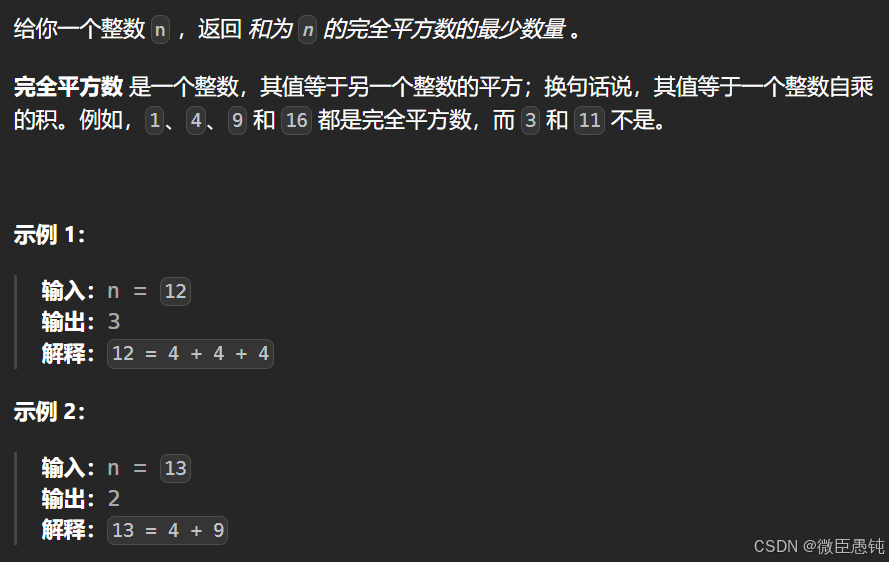
求求最小数，遍历顺序不重要

dp[j]：和为j的完全平方数的最少数量为dp[j]超简单，和零钱兑换的原理一样

class Solution {
public:int numSquares(int n) {vector<int> dp(n+1,INT_MAX);dp[0]=0;for(int i=1;i*i<=n;i++) //遍历物品{for(int j=i*i;j<=n;j++){dp[j]=min(dp[j],dp[j-i*i]+1);}}return  dp[n];}
};

🎯三、子序列LSCDP 【线性DP的一个分支】

“子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序”。

（1）895. 最长上升子序列 - AcWing题库

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

①dp[i]表示以nums[i]结尾的最长递增子序列的长度

②位置i的最长升序子序列等于 j从0到i-1各个位置的最长升序子序列 + 1 的最大值。

所以转移方程：if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1)

③初始化：每一个i，对应的dp[i]（即最长递增子序列）起始大小至少都是1

比较简单~~~

【acwing】动态规划系列_acwing memset dp-CSDN博客含有此题

（2）674. 最长连续递增序列 - 力扣（LeetCode）

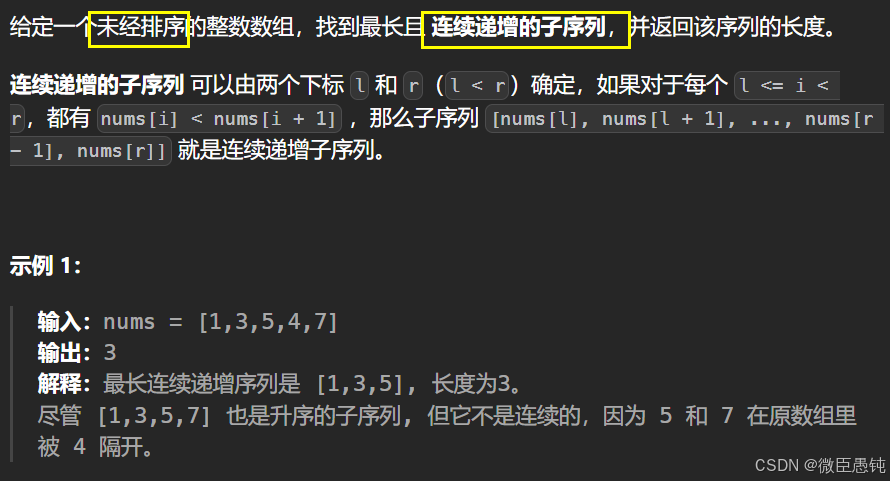
自己写的，一遍AC！！！！！！！！！！

class Solution {
public:int findLengthOfLCIS(vector<int>& nums) {vector<int> dp(nums.size(),1);//dpfor(int i=1;i<nums.size();i++){if(nums[i-1]<nums[i])//连续记录dp[i]=max(dp[i],dp[i-1]+1);}//找最长的int res=0;for(auto it:dp){res=max(res,it);}return res;}
};

（3）最长公共子序列 - acwing

【acwing】动态规划系列_acwing memset dp-CSDN博客

博客中有这道题

数组索引从1开始

dp[i][j]: a数组中以i结尾和b数组中以j结尾的最长公共子序列

a[i] 和b[j] 相等： dp[i][j]=dp[i-1][j-1]+1;

不相等：则选择去掉s1的一个字符或去掉s2的一个字符, 最大的公共子序列长度来自于去掉一个字符的情况,这里求max,dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])

喝喝，一开始初始化的时候写的int dp ，应该是char dp!!!!!!

（4）1035. 不相交的线 - 力扣

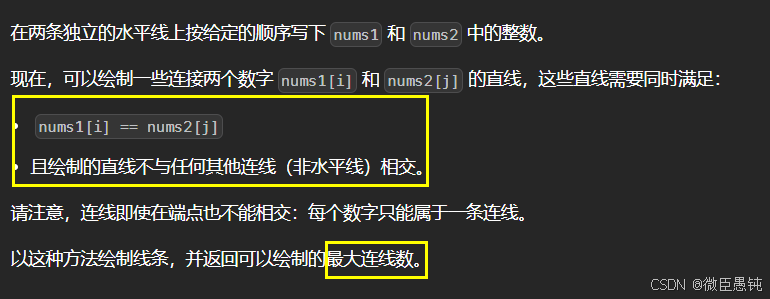
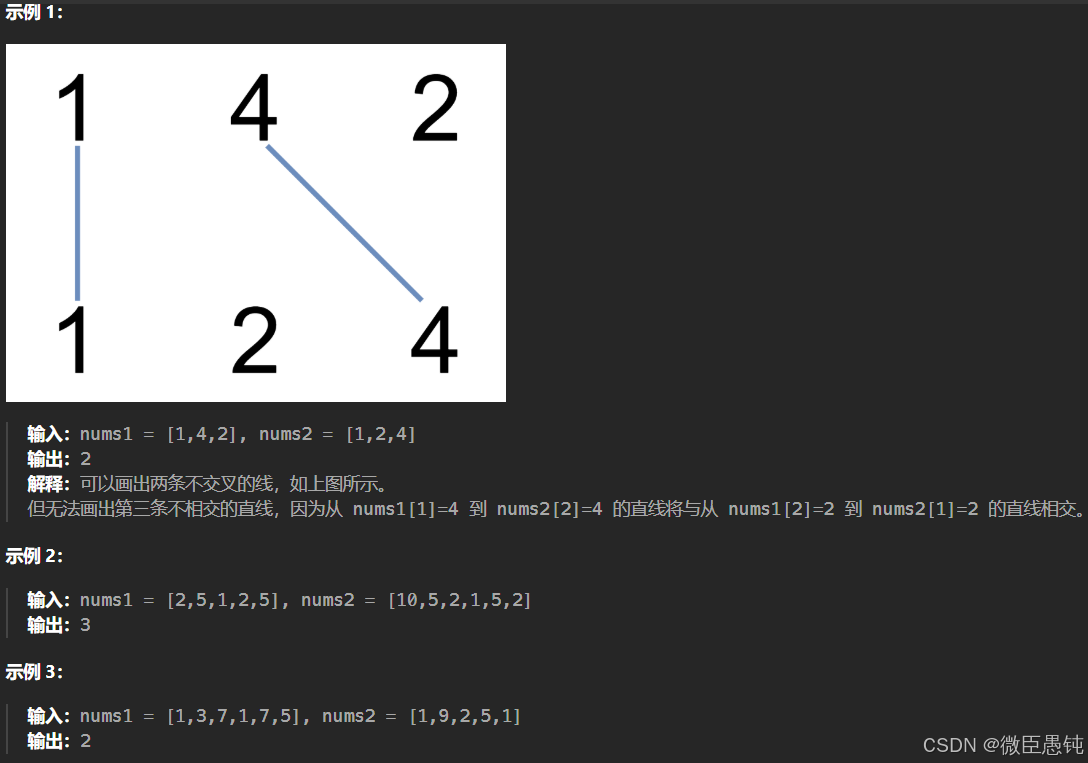
题目看起来挺抽象的，其实转换以下题意就是：直线不能相交，说明在字符串nums1中找到一个与字符串nums2相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，连接相同数字的直线就不会相交。所以！！本题说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度！

数组索引从0开始，但 dp 数组的大小是 (n + 1) × (m + 1)，由于 dp 数组的大小是 (n + 1) × (m + 1)，dp[n][m] 正好对应于 nums1 和 nums2 的完整长度

所以需要判断的是nums1[i-1]==nums2[j-1]

class Solution {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {int n = nums1.size();int m = nums2.size();// dp[i][j] 表示 nums1 的前 i-1 个元素和 nums2 的前 j-1 个元素的最长公共子序列长度vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));// 动态规划填表for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {if (nums1[i - 1] == nums2[j - 1]) {// 如果当前元素相等，则在之前的基础上加 1dp[i][j] = dp[i - 1][j - 1] + 1;} else {// 如果当前元素不相等，则取两种情况的最大值dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}// 返回最终结果，即 nums1 和 nums2 的最长公共子序列长度return dp[n][m];}
};

（5）718. 最长重复子数组 - （最长连续公共子序列）

子数组，其实就是连续子序列。注意区分与最长公共子序列问题的求解差异

①dp数组的含义：dp[i][j] ----以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j] （注意是i-1,所以遍历的时候要从1开始）

②转移方程：当A[i - 1] 和B[j - 1]相等的时候，dp[i][j] = dp[i - 1][j - 1] + 1

③初始化：根据dp[i][j]的定义，dp[i][0] 和dp[0][j]其实都是没有意义的，为了后续可以正常递推，dp[i][0] 和dp[0][j]均初始化为0

④遍历顺序：先遍历a还是b都行

⑤举例推导：

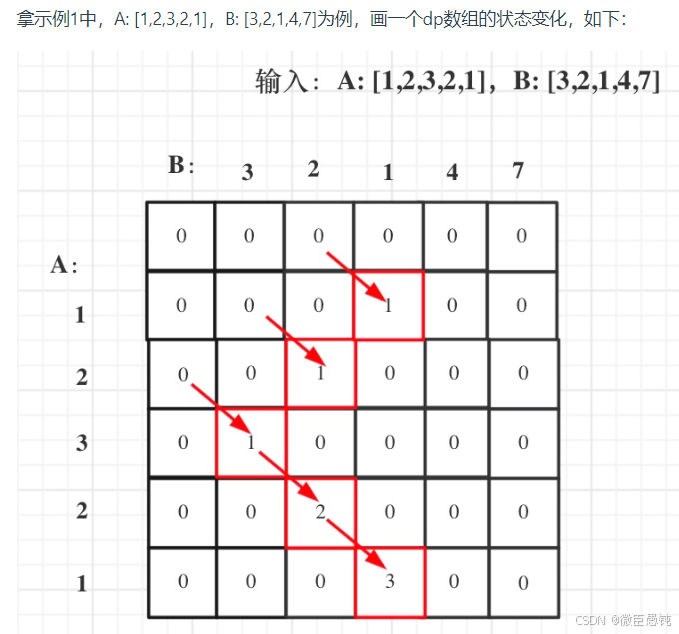
class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {//定义dp数组int n=nums1.size();int m=nums2.size();vector<vector<int>> dp(n+1,vector<int>(m+1,0));int res=0;////dpfor(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(nums1[i-1]==nums2[j-1])dp[i][j]=dp[i-1][j-1]+1;res=max(res,dp[i][j]);}}return res;}
};

注意数组索引从0开始，第一遍写的时候没定义res记录最大值~~~~ 呜呜呜

滚动数组优化：

dp[i][j]都是由dp[i - 1][j - 1]推出。那么压缩为一维数组，也就是dp[j]都是由dp[j - 1]推出。

也就是相当于可以把上一层dp[i - 1][j]拷贝到下一层dp[i][j]来继续用。

class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {//定义dp数组int n=nums1.size();int m=nums2.size();vector<int> dp(n+1,0);int res=0;////dpfor(int i=1;i<=n;i++){for(int j=m;j>0;j--){if(nums1[i-1]==nums2[j-1])dp[j]=dp[j-1]+1;else dp[j] = 0; // 注意这里不相等的时候要有赋0的操作res=max(res,dp[j]);}}return res;}
};

拓展：

如果dp[i][j]为以下标i为结尾的A，和以下标j 为结尾的B，最长重复子数组长度

那么第一行和第一列毕竟要进行初始化，如果nums1[i] 与 nums2[0] 相同的话，对应的 dp[i][0]就要初始为1，因为此时最长重复子数组为1。 nums2[j] 与 nums1[0]相同的话，同理。

// 版本三
class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {vector<vector<int>> dp (nums1.size() + 1, vector<int>(nums2.size() + 1, 0));int result = 0;// 要对第一行，第一列经行初始化for (int i = 0; i < nums1.size(); i++) if (nums1[i] == nums2[0]) dp[i][0] = 1;for (int j = 0; j < nums2.size(); j++) if (nums1[0] == nums2[j]) dp[0][j] = 1;for (int i = 0; i < nums1.size(); i++) {for (int j = 0; j < nums2.size(); j++) {if (nums1[i] == nums2[j] && i > 0 && j > 0) { // 防止 i-1 出现负数dp[i][j] = dp[i - 1][j - 1] + 1;}if (dp[i][j] > result) result = dp[i][j];}}return result;}
};

（6）53. 最大子数组和 - 力扣

①dp含义：dp[i]：包括下标i（以nums[i]为结尾）的最大连续子序列和为dp[i]

②转移方程：

dp[i]只有两个方向可以推出来：

dp[i - 1] + nums[i]，即：nums[i]加入当前连续子序列和
nums[i]，即：从头开始计算当前连续子序列和（没考虑到这种情况，因为是连续的！！！）

一定是取最大的，所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);

③初始化：dp[0] = nums[0]

class Solution {
public:int maxSubArray(vector<int>& nums) {//找最大和的连续子数组if (nums.size() == 0) return 0;//dp[i][j]:以i-1结尾的连续子数组的和vector<int> dp(nums.size());dp[0]=nums[0];int res=dp[0];//dpfor(int i=1;i<nums.size();i++){dp[i]=max(nums[i],dp[i-1]+nums[i]);res=max(res,dp[i]);}return res;}
};

dp 的大小应该是 nums.size()，以便索引范围从 0 到 nums.size() - 1

（7） 392. 判断子序列 - 力扣

编辑距离的入门题目

dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]

if (s[i - 1] == t[j - 1])，那么dp[i][j] = dp[i - 1][j - 1] + 1

if (s[i - 1] != t[j - 1])，此时相当于t要删除元素 dp[i][j] = dp[i][j - 1]

最终判断dp[n][m]是否和 s子串的长度相等

【和 1143.最长公共子序列 (opens new window)的递推公式基本那就是一样的，区别就是本题如果删元素一定是字符串t，而最长公共子序列是两个字符串都可以删元素。】

class Solution {
public:bool isSubsequence(string s, string t) {int n = s.length(); // 获取字符串 s 的长度int m = t.length(); // 获取字符串 t 的长度// dp[i][j] 以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));// 遍历字符串 s 和 tfor (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {if (s[i - 1] == t[j - 1]) {// 如果当前字符匹配，则最长公共子序列长度加 1dp[i][j] = dp[i - 1][j - 1] + 1;} else {// 如果当前字符不匹配，则取 t 的前 j-1 个字符与 s 的前 i 个字符的最长公共子序列长度// 因为 dp[i][j] 已经初始化为 0，所以这里可以直接赋值dp[i][j] = max(dp[i][j], dp[i][j - 1]);}}}// 如果 s 是 t 的子序列，则 dp[n][m] 应该等于 s 的长度 n// 因为 s 的所有字符都必须在 t 中按顺序出现if (dp[n][m] == n) return true;else return false;}
};

（8）拍照【最长山峰子序列】---已发博客，点击标题跳转

在这里总结一下，就是用两个dp，一个求最长上升子序列，一个求最长下降子序列（也就是倒序最长上升，改一下遍历顺序就可以啦）

dp1 (最长上升子序列)：

dp2 (最长下降子序列)：

最终结果（最少出队人数）是总长度(n)减去可以组成的最长序列的长度（dp1+dp2-1）

（9）72. 编辑距离 - 力扣

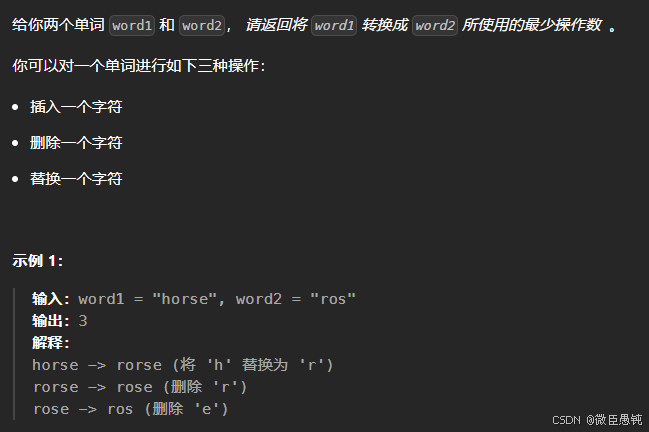
【acwing】动态规划系列_acwing memset dp-CSDN博客 ----最短编辑距离【同款题目】

①dp定义：dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]

②转移方程：

if (word1[i - 1] == word2[j - 1])不操作 dp[i][j] = dp[i - 1][j - 1]
if (word1[i - 1] != word2[j - 1])① 增
//word2添加一个元素，相当于word1删除一个元素② 删
//word1删除一个元素，那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作
dp[i][j] = dp[i - 1][j] + 1
//操作二：word2删除一个元素，那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作
dp[i][j] = dp[i][j - 1] + 1③ 换
//替换元素，word1替换word1[i - 1]，使其与word2[j - 1]相同，此时不用增删加元素。if (word1[i - 1] == word2[j - 1])的时候我们的操作 是 dp[i][j] = dp[i - 1][j - 1] ，那么只需要一次替换的操作，就可以让 word1[i - 1] 和 word2[j - 1] 相同。所以 dp[i][j] = dp[i - 1][j - 1] + 1

综上，当 if (word1[i - 1] != word2[j - 1]) 时取最小的，即：dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;

③初始化：

dp[i][0] 和 dp[0][j] 表示什么呢？

dp[i][0] ：以下标i-1为结尾的字符串word1，和空字符串word2，最近编辑距离为dp[i][0]。

那么dp[i][0]就应该是i，对word1里的元素全部做删除操作，即：dp[i][0] = i;

同理dp[0][j] = j;

class Solution {
public:int minDistance(string s, string t) {//定义dp数组vector<vector<int>> dp(s.size()+1,vector<int>(t.size()+1,0));//初始化dp[i][0]  dp[0][j]for(int i=1;i<=s.size();i++) dp[i][0]=i;for(int j=1;j<=t.size();j++) dp[0][j]=j;//dpfor(int i=1;i<=s.size();i++){for(int j=1;j<=t.size();j++){if(s[i-1]==t[j-1])dp[i][j]=dp[i-1][j-1];elsedp[i][j]=min({dp[i-1][j-1],dp[i-1][j],dp[i][j-1]})+1;}}return dp[s.size()][t.size()];}
};

dp理论知识🔥🔥

🎯一、线性DP

（1）🚀斐波那契数 -入门级

（2）🚀898. 数字三角形-acwing ---入门级

（3）往期题目

①选数异或：在 [l, r] 区间是否能找到 a[i] ^ a[j] = x 的数对？

②🚀破损的楼梯：

③🚀安全序列：

🎯二、背包问题 ✅✅✅【很重要！！】

（1） 494. 目标和 - 力扣 --(0-1背包) 【给定背包容量，装满背包有多少种方法】

🤯🤯🤯🤯🤯🤯🤯🤯🤯

（2）322. 零钱兑换 - 力扣（完全背包）--

（3）518. 零钱兑换 II - 力扣（完全背包）-和25-3-2的csp题基本一样

（4）377. 组合总和 Ⅳ - 力扣（LeetCode） --完全背包

（5）57. 爬楼梯 （卡玛）

🤯🤯🤯🤯🤯🤯🤯🤯🤯

（6）46. 携带研究材料（0-1背包）【 给定背包容量 装满背包 的最大价值是多少】

（7）最快洗车时间（0-1）背包

（8）474. 一和零 - 力扣 （0-1背包）【给定背包容量，装满背包最多有多少个物品】

（9）279. 完全平方数 -（完全背包）

🎯三、子序列LSCDP 【线性DP的一个分支】

（1）895. 最长上升子序列 - AcWing题库

（2）674. 最长连续递增序列 - 力扣（LeetCode）

（3）最长公共子序列 - acwing

（4）1035. 不相交的线 - 力扣

（5）718. 最长重复子数组 - （最长连续公共子序列）

（6）53. 最大子数组和 - 力扣

（7） 392. 判断子序列 - 力扣

（8）拍照【最长山峰子序列】---已发博客，点击标题跳转

（9）72. 编辑距离 - 力扣

相关文章：

①选数异或：在 `[l, r]` 区间是否能找到 `a[i] ^ a[j] = x` 的数对？

（5）57. 爬楼梯（卡玛）

（6）46. 携带研究材料（0-1背包）【给定背包容量装满背包的最大价值是多少】

（8）474. 一和零 - 力扣（0-1背包）【给定背包容量，装满背包最多有多少个物品】