当前位置：首页 > news >正文

全排列|| 分发饼干摆动序列

news 来源：原创 2025/7/27 13:53:03

1.给定一个可包含重复数字的序列 nums ，按任意顺序返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]

输出： [[1,1,2], [1,2,1], [2,1,1]]

示例 2：

输入：nums = [1,2,3]

输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

1 <= nums.length <= 8

-10 <= nums[i] <= 10

#include <bits/stdc++.h>
using namespace std;
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& num,vector<bool>& used)
{
   if(path.size()==num.size())
   {
       result.push_back(path);
       return ;
   }
   for(int i=0;i<num.size();i++)
   {
       if(i>0&&num[i]==num[i-1]&&used[i-1]==false)
       continue;
       if(used[i]==true)
       continue;
       used[i]=true;
       path.push_back(num[i]);
       backtracking(num,used);
       used[i]=false;
       path.pop_back();
   }

}
vector<vector<int>> combine(vector<int>& num)
{
    result.clear();
    path.clear();
    vector<bool> used(num.size(),false);
    backtracking(num,used);
    return result;
}
int main()
{
    vector<int> num={1,1,2};
    vector<vector<int>> t=combine(num);
    for(const auto& m:t)
    {
        for(int n:m)
        {
            cout<<n<<" ";
       }
       cout<<endl;
   }
    return 0;
}

思路：以示例中的 [1,1,2]为例抽象为一棵树，去重过程如图：

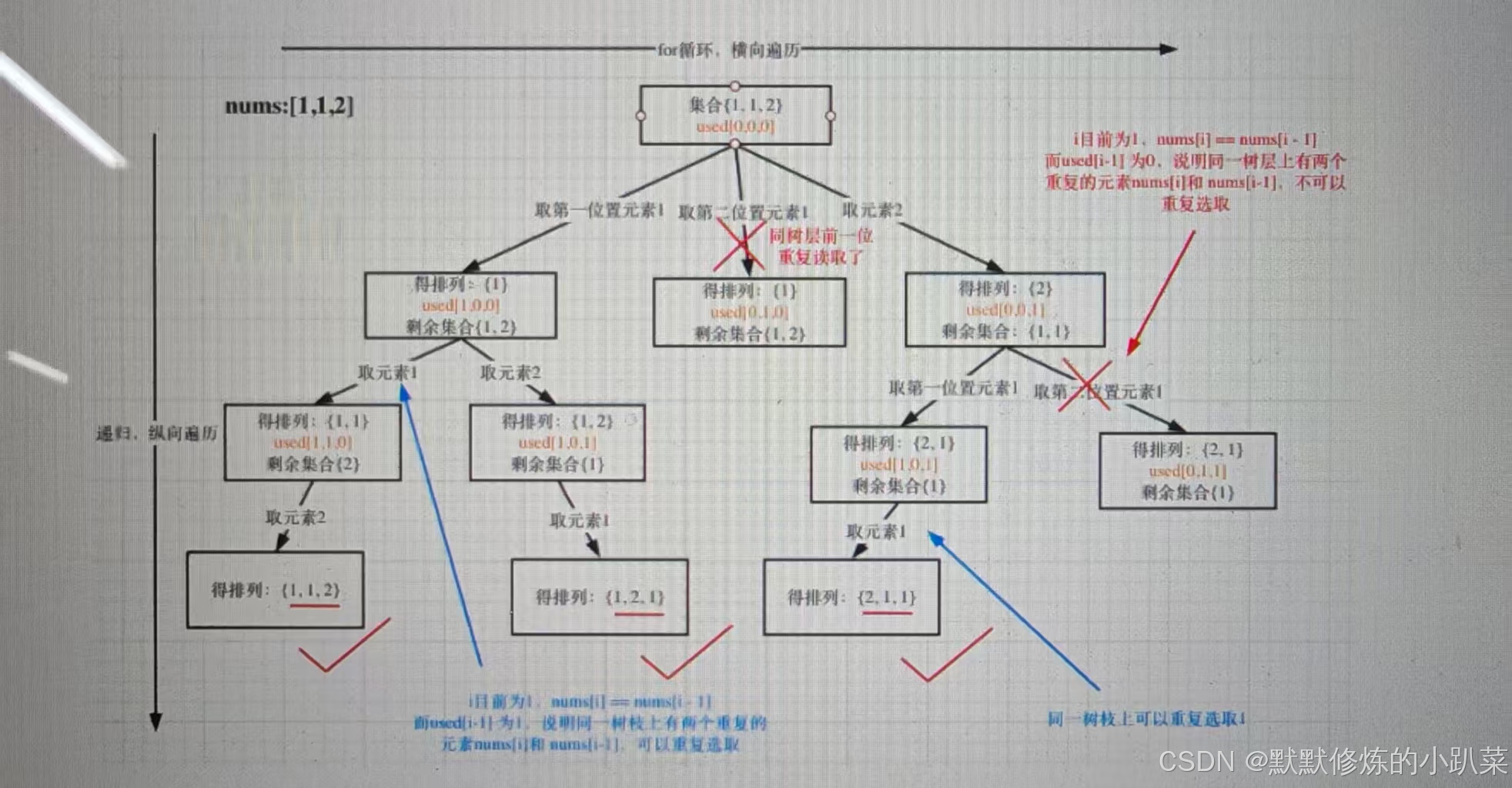
图中我们对同一树层，前一位（也就是nums[i-1]）如果使用过，那么就进行去重。

一般来说：组合问题和排列问题是在树形结构的叶子节点上收集结果，而子集问题就是取树上所有节点的结果。这与之前全排列的思路类似，就多了去重，更多细节可以参考之前的文章。

2.假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

#include <bits/stdc++.h>
using namespace std;
int find(vector<int>& g,vector<int>& s)
{
   sort(g.begin(),g.end());
   sort(s.begin(),s.end());
   int result=0;
   int index=s.size()-1;
   for(int i=g.size()-1;i>=0;i--)
   {
       while(index>0&&s[index]>=g[i])
       {
           result++;
           index--;
       }
   }
   return result;
}
int main()
{
   vector<int> g={1,2,7,10};
   vector<int> s={1,3,5,9};
   int t=find(g,s);
   cout<<t;
   return 0;
}

思路：

为了满足更多的小孩，就不要造成饼干尺寸的浪费。大尺寸的饼干既可以满足胃口大的孩子也可以满足胃口小的孩子，那么就应该优先满足胃口大的。这里的局部最优就是大饼干喂给胃口大的，充分利用饼干尺寸喂饱一个，全局最优就是喂饱尽可能多的小孩。可以尝试使用贪心策略，先将饼干数组和小孩数组排序。然后从后向前遍历小孩数组，用大饼干优先满足胃口大的，并统计满足小孩数量。

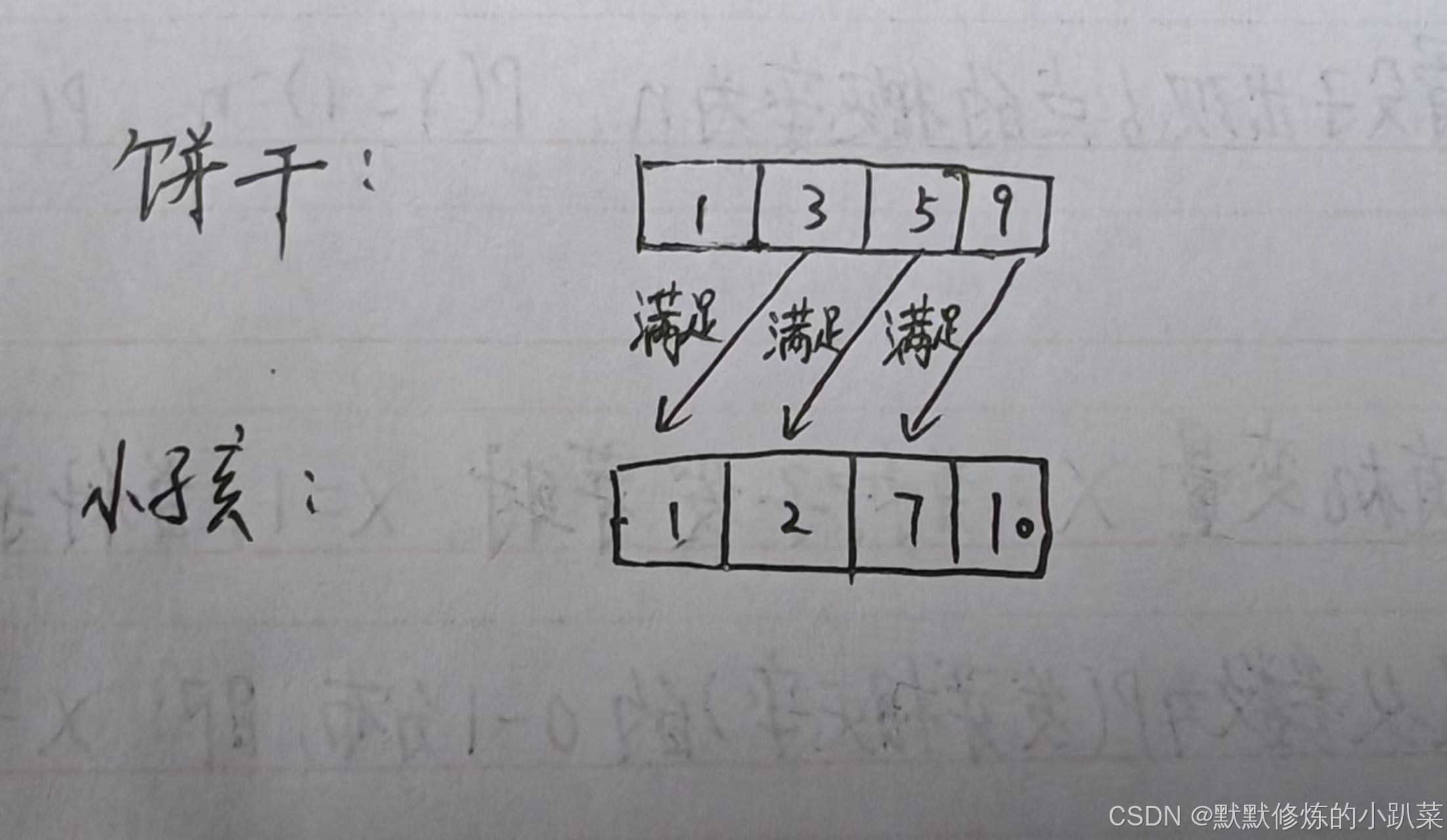
这个例子可以看出饼干 9 只有喂给胃口为 7 的小孩，这样才是整体最优解，并想不出反例。

代码中用了 index 来控制饼干数组的遍历，遍历饼干并没有再起一个 for 循环，而是采用自减的方式，这也是常用的技巧。

3.如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第一个差（如果存在的话）可能是正数或负数。少于两个元素的序列也是摆动序列。

例如， [1,7,4,9,2,5] 是一个摆动序列，因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

给定一个整数序列，返回作为摆动序列的最长子序列的长度。通过从原始序列中删除一些（也可以不删除）元素来获得子序列，剩下的元素保持其原始顺序。

#include <bits/stdc++.h>
using namespace std;
int wiggle(vector<int>& num)
{
   if(num.size()<=1)
   return num.size();
   int preDiff=0;
   int curDiff=0;
   int result=1;
   for(int i=0;i<num.size()-1;i++)
   {
       curDiff=num[i+1]-num[i];
       if((preDiff>=0&&curDiff<0)||preDiff<=0&&curDiff>0)
       {
           result++;
           curDiff=preDiff;
       }
   }
   return result;
}
int main()
{
   vector<int> num={1,7,4,9,2,5};
   int t=wiggle(num);
   cout<<t;
   return 0;
}

思路：本题要求通过从原始序列中删除一些（也可以不删除）元素来获得子序列，剩下的元素保持其原始顺序。我们来分析一下，要求删除元素使其达到最大摆动序列，应该删除什么元素呢？

如图所示：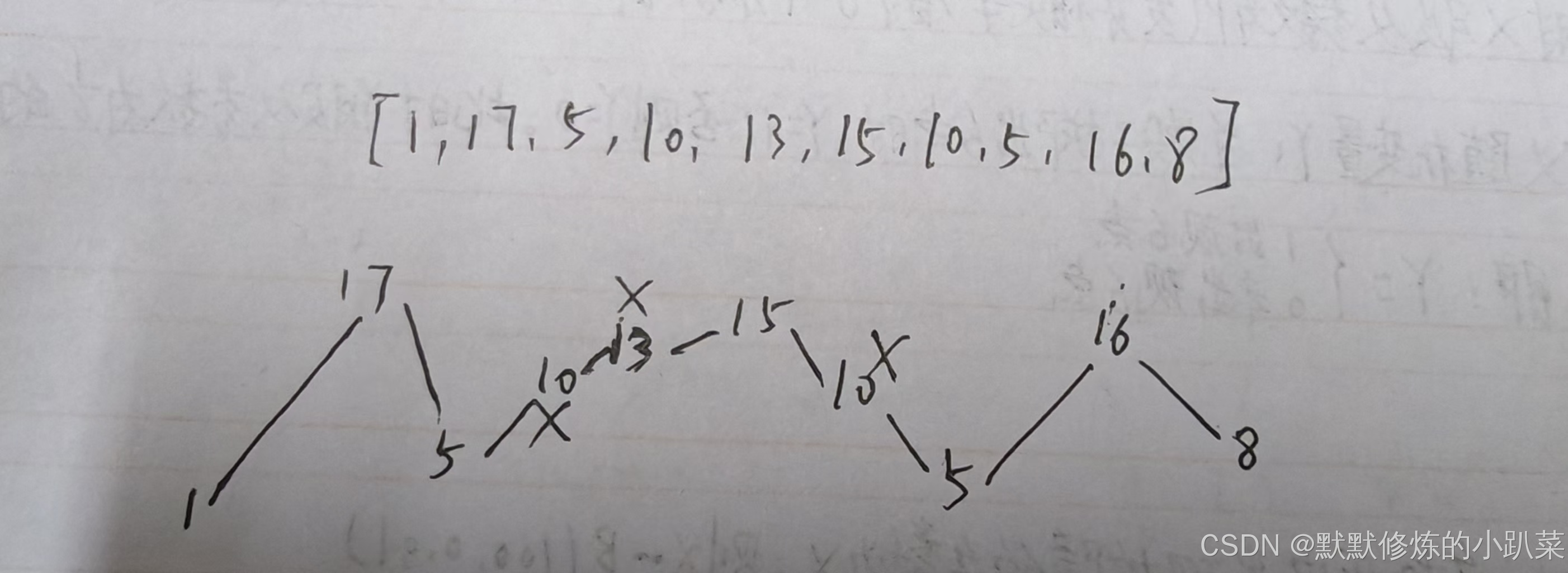

局部最优：删除单调坡度上的节点（不包括单调坡度两端的节点），那么这个坡度就可以有两个局部峰值。

整体最优：整个序列有最多的局部峰值，从而达到最长摆动序列。

实际操作上，其实连删除的操作都不用做，因为题目要求的是最长摆动子序列的长度，所以只需要统计数组的峰值数量就可以了（相当于是删除单一坡度上的节点，然后统计长度）

这就是贪心所贪的地方，让峰值尽可能的保持峰值，然后删除单一坡度上的节点。

在计算是否有峰值的时候，大家知道遍历的下标 i ，计算 prediff（nums[i] - nums[i-1]）和 curdiff（nums[i+1] - nums[i]），如果prediff < 0 && curdiff > 0 或者 prediff > 0 && curdiff < 0 此时就有波动就需要统计。

这是我们思考本题的一个大体思路，但本题要考虑三种情况：

情况一：上下坡中有平坡

情况二：数组首尾两端

情况三：单调坡中有平坡

情况一：上下坡中有平坡，例如 [1,2,2,2,2,1]这样的数组，如图：

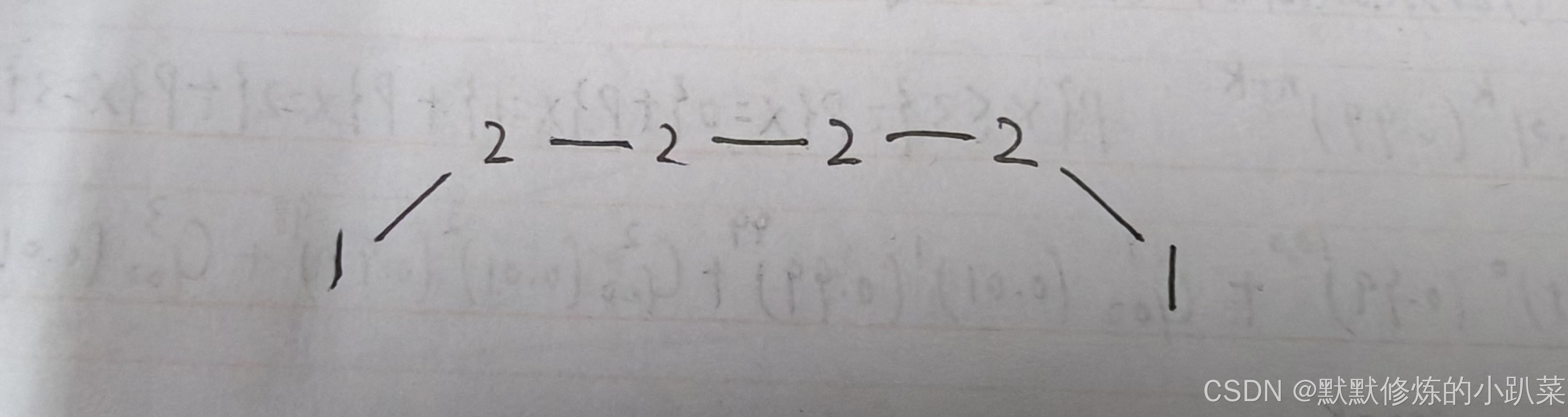
它的摇摆序列长度是多少呢？ 其实是长度是 3，也就是我们在删除的时候要不删除左面的三个 2，要不就删除右边的三个 2。

如图，可以统一规则，删除左边的三个 2：

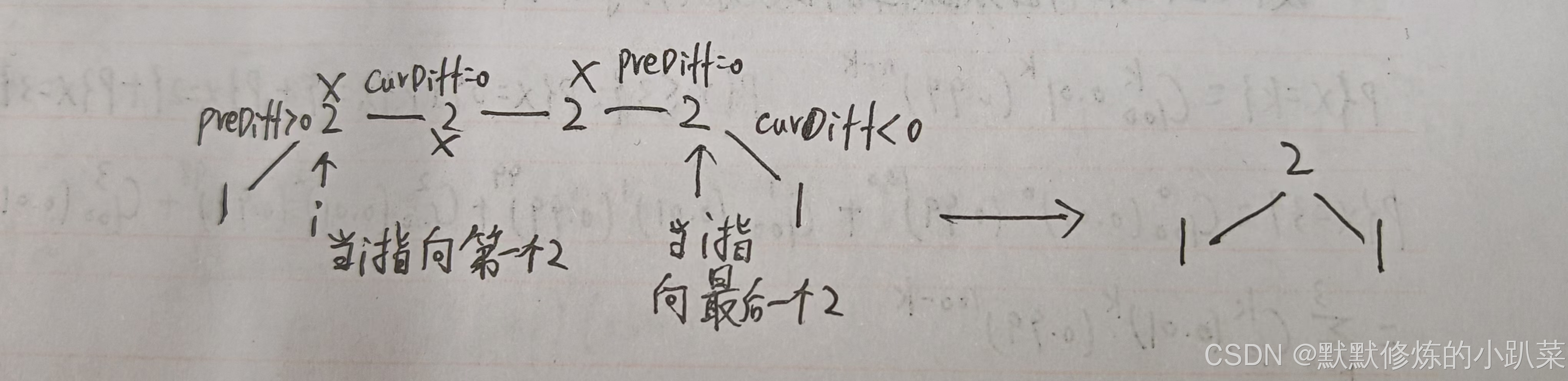
在图中，当 i 指向第一个 2 的时候，prediff > 0 && curdiff = 0 ，当 i 指向最后一个 2 的时候 prediff = 0 && curdiff < 0。

如果我们采用，删左面三个 2 的规则，那么当 prediff = 0 && curdiff < 0 也要记录一个峰值，因为他是把之前相同的元素都删掉留下的峰值。

所以我们记录峰值的条件应该是： (preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)，为什么这里允许 prediff == 0 ，就是为了上面我说的这种情况。

情况二：数组首尾两端

针对以上情形，result 初始为 1（默认最右面有一个峰值），此时 curDiff > 0 && preDiff <= 0，那么 result++（计算了左面的峰值），最后得到的 result 就是 2（峰值个数为 2 即摆动序列长度为 2）

情况三：单调坡度有平坡

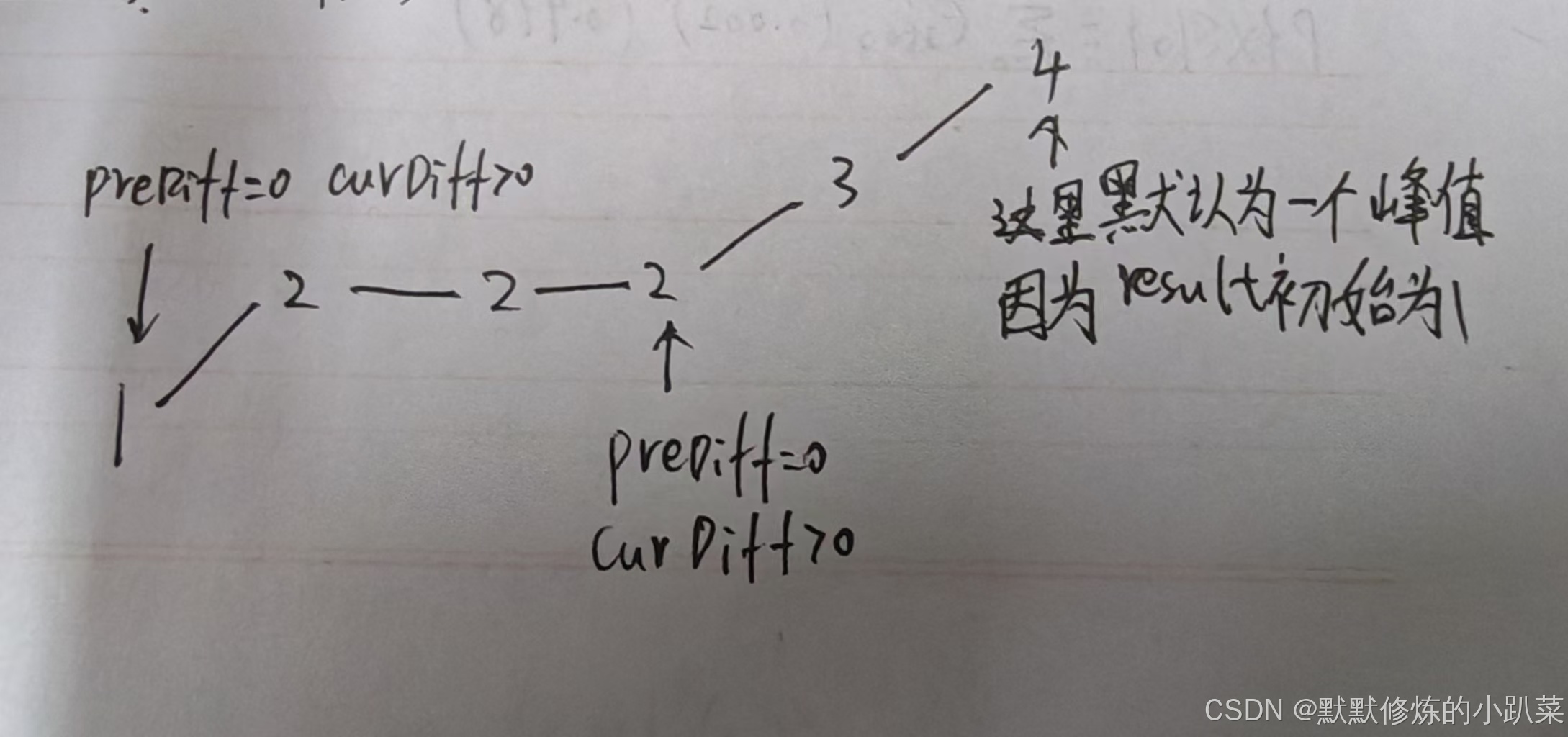
图中，我们可以看出，按照先前思路会在三个地方记录峰值，但其实结果因为是 2，因为单调中的平坡不能算峰值（即摆动）。之所以会出问题，是因为我们实时更新了 prediff。对于修改我们只需要在这个坡度摆动变化的时候，更新 prediff 就行，这样 prediff 在单调区间有平坡的时候就不会发生变化，造成我们的误判。

相关文章：