当前位置：首页 > news >正文

2025美国大学生数学建模竞赛（美赛）B题完整思路分析论文（35页）（含模型、可运行代码和运行结果）

news 来源：原创 2025/5/21 21:31:24

2025美国大学生数学建模竞赛B题完整思路分析论文

摘要

一、问题重述

二、问题分析

三、模型假设

四、模型建立与求解

4.1问题1

4.1.1问题1思路分析

4.1.2问题1模型建立

4.1.3问题1样例代码（仅供参考）

4.1.4问题1样例代码运行结果（仅供参考）

4.2问题2

4.2.1问题2思路分析

4.2.2问题2模型建立

4.2.3问题2样例代码（仅供参考）

4.2.4问题2样例代码运行结果（仅供参考）

4.3问题3

4.3.1问题3思路分析

4.3.2问题3模型建立

4.3.3问题3样例代码（仅供参考）

4.3.4问题3样代结果和备忘录（仅供参考）

五、模型优缺点

六、模型推广

助攻资料下载链接: 2025美赛数模B助攻资料https://pan.baidu.com/s/1m4NxtdFSmN5lI0lBgnZs2Q 提取码: bkgz 复制这段内容后打开百度网盘手机App，操作更方便哦

摘要

本论文旨在为阿拉斯加州朱诺市构建一个可持续旅游业模型，旨在平衡经济收入和环境影响，推动旅游业的可持续发展。通过考虑游客数量、收入以及环保政策等因素，模型的优化目标是最大化旅游收入的同时，最小化环境影响。通过灵敏度分析，识别了对结果影响最大的关键因素，并提出了如何通过额外收入进行支出的计划，以促进可持续旅游的发展。

在问题1中，我们构建了一个详细的可持续旅游业模型，涉及游客数量、整体收入和环保政策等多个因素。模型的优化目标明确，即最大化收入并最小化环境影响。我们考虑了如税费、游客数量限制和环保措施等因素，并通过灵敏度分析确定了对结果影响最为显著的因素。模型还包括了额外收入的支出计划，这些收入将用于改善基础设施和支持环保项目，从而为可持续旅游创造条件。

问题2中，我们探讨了如何将朱诺市的模型应用到其他受过度旅游影响的目的地，并分析了地点选择如何影响需要采取的措施。通过调整模型中的参数（如税费、游客上限和环保政策等），我们展示了如何根据不同地区的特点制定相应的政策措施，尤其是通过分流游客至较少游客的景点来实现更均衡的游客分布，减轻热门景点的压力。

问题3则要求我们根据模型预测的结果，撰写一份给朱诺市旅游委员会的备忘录，提出优化旅游业的建议。备忘录中详细分析了各种政策措施（如增加税费、游客数量限制和环保措施等）的实施效果，并根据模型结果提供了如何优化旅游业的具体建议，确保朱诺市旅游业的收入增长与环境保护并重。

综上所述，本论文不仅为朱诺市提供了可持续旅游发展的理论支持，还为全球类似地区提供了有价值的参考，展示了如何平衡经济利益与环境保护，推动可持续旅游发展。

关键词：可持续旅游，模型优化，灵敏度分析，旅游政策

助攻资料下载链接: 2025美赛数模B助攻资料https://pan.baidu.com/s/1m4NxtdFSmN5lI0lBgnZs2Q

提取码: bkgz 复制这段内容后打开百度网盘手机App，操作更方便哦

一、问题重述

问题1：构建可持续旅游业模型

本问题要求构建一个适用于阿拉斯加州朱诺市（Juneau）的可持续旅游业模型。在模型中，需要考虑游客数量、整体收入以及为稳定旅游业所采取的各种措施。目标是明确哪些因素需要优化（如收入最大化与环境影响最小化），同时界定哪些因素作为约束条件（如游客数量限制、环境影响阈值等）。此外，还需提出如何利用额外收入进行支出，并说明这些支出如何回馈到模型中，进一步促进旅游业的可持续发展。模型应包括灵敏度分析，探讨哪些因素对最终结果的影响最大。

问题2：模型在其他旅游目的地的适用性

在此问题中，需要演示如何将所建立的朱诺市旅游业模型应用于其他受过度旅游影响的目的地。考虑到不同目的地的特点（如自然环境、社会文化及旅游资源），模型应如何调整参数以适应新的目的地需求。分析中需要探讨地点选择如何影响哪些措施将变得更为重要。模型还需探讨如何通过优化游客流量，尤其是推广游客较少的景点，以实现更好的游客分布，从而缓解热门景点的过度拥挤，达到更平衡的旅游发展。

问题3：备忘录编写

在此问题中，需要撰写一份针对朱诺市旅游委员会的备忘录，概述通过模型预测的结果，并分析不同政策（如税费增加、游客数量限制、环保政策等）对旅游业收入与环境影响的潜在作用。同时，基于模型结果，提出如何优化旅游业的建议。备忘录应简明扼要地讨论各项措施的效果，并提出具体的优化策略，如调整税费、分流游客、加强环保政策等，确保朱诺市在保持旅游收入增长的同时，实现旅游业的可持续性。

二、问题分析

问题1：构建可持续旅游业模型

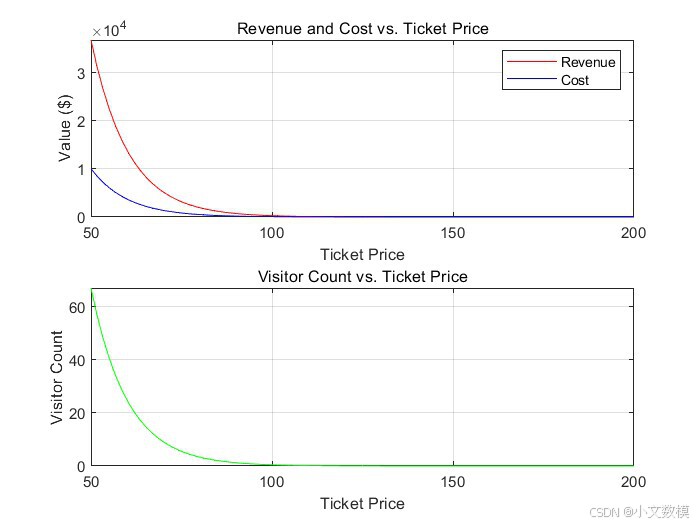
在问题1中，我们需要为朱诺市构建一个可持续旅游业模型，考虑的因素包括游客数量、旅游收入以及采取的稳定旅游的措施。我们设定的优化目标是最大化旅游收入，同时最小化环境影响。为此，我们假设游客数量与税费、游客数量限制和环保政策之间存在线性关系，收入与游客数量成正比，而环境影响与游客数量同样呈线性关系。模型中设定了约束条件，如游客数量不能超过上限，环境影响必须保持在可接受范围内，收入必须达到最低要求。额外的收入将用于基础设施建设、环保项目等，以确保这些支出促进可持续发展。此外，灵敏度分析将帮助识别对优化结果影响较大的因素，如税费调整和游客限流，这为政策制定提供了实证依据。

问题2：模型在其他旅游目的地的适用性

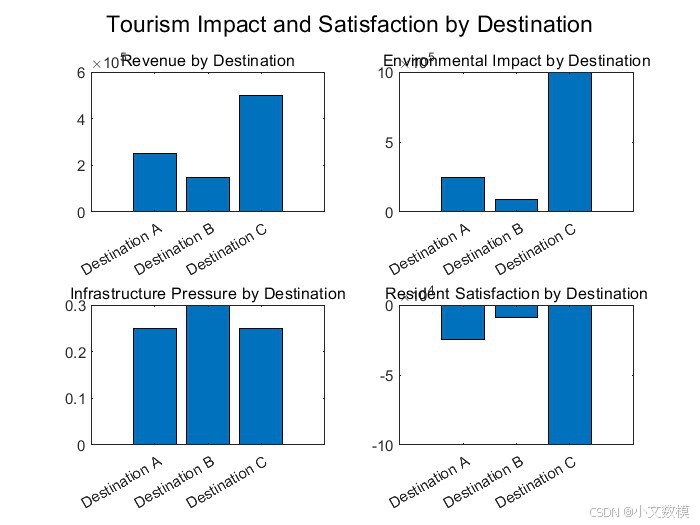
在问题2中，我们探讨了如何将构建的模型应用到其他受过度旅游影响的旅游目的地，并分析了地点差异对措施选择的影响。由于不同地区的自然环境、社会文化、旅游基础设施等条件的差异，模型的参数（如税费、游客数量限制、环保政策等）需要根据具体情况进行调整。例如，在生态脆弱的地区，需要加强环保政策和游客流量的控制；而在交通繁忙的地区，限制游客数量和优化游客流量分布可能更为重要。通过模型，我们可以促使游客分流到不那么拥挤的景点，推广一些未充分开发的景点，以缓解热门景点的压力，并帮助这些地区实现更加均衡的旅游发展。

问题3：备忘录编写

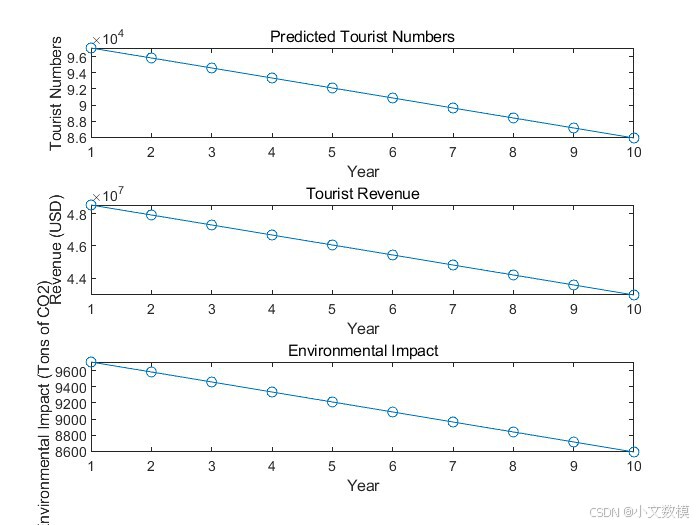
在问题3中，我们要求根据问题1中的模型结果向朱诺市旅游委员会提交一份备忘录，分析不同政策措施的效果，并给出优化旅游业的建议。备忘录将基于模型预测的结果，分析如税费增加、游客限制和环保政策等措施对旅游收入和环境影响的潜在作用。我们会评估这些措施的实施成本与收益，并根据灵敏度分析的结果，推荐哪些因素需要优先调整。最终，我们会提供一系列可行的优化策略，如合理的税费调整、有效的游客数量限制以及绿色环保政策，确保朱诺市在保持经济增长的同时，实现旅游业的可持续发展。

助攻资料下载链接: 2025美赛数模B助攻资料https://pan.baidu.com/s/1m4NxtdFSmN5lI0lBgnZs2Q

提取码: bkgz 复制这段内容后打开百度网盘手机App，操作更方便哦

助攻资料下载链接: 2025美赛数模B助攻资料https://pan.baidu.com/s/1m4NxtdFSmN5lI0lBgnZs2Q

提取码: bkgz 复制这段内容后打开百度网盘手机App，操作更方便哦

相关文章：