【数据结构 · 初阶】- 快速排序
目录
一. Hoare 版本
1. 单趟
2. 整体
3. 时间复杂度
4. 优化(抢救一下)
4.1 随机选 key
4.2 三数取中
二. 挖坑法
格式优化
三. 前后指针(最好)
四. 小区间优化
五. 改非递归
快速排序是 Hoare 提出的一种基于二叉树结构的交换排序方法。统一排升序
一. Hoare 版本
1. 单趟
目的:选出一个关键字/关键值/基准值 key,把他放到排好序后,最终在的位置
key 都喜欢在最左/右边,其他位置不好排
例如这样的数组:

单趟结束后要达成这样的效果:(选择,插入,冒泡排序的单趟没有这种附加效果)
 此时6就在排好序后,所在的位置
此时6就在排好序后,所在的位置
实现:
R 往左走,找比 key 小的;L 往右走,找比 key 大的,相等无所谓。都找到之后,交换。直至相遇
结论:key 在左,让 R 先走,能保证相遇位置一定比 key 小。 key 在右,让 L 先走。
相遇位置既然比 key 小,就把 key 换到左边




void QuickSort(int* a, int left, int right)
{int begin = left, end = right;int keyi = left;while (left < right){while (left < right && a[right] >= a[keyi]) // 右边找小right--; // 且要防止本来就有序,right 飘出去while (left < right && a[left] <= a[keyi]) // 左边找大left++;Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);keyi = left;
}易错:
1. 不能认为外面的 while 判断过了,里面就不用判断。里面的 while 会多走几次,left 和 right 的相对位置变了,所以要再加判断。
2. 一定是 >= 否则可能出现死循环
2. 整体
递归:
上面排好单趟,被分成三段区间,[begin, keyi-1] keyi [keyi+1, end]。左右区间都无序,递归左区间。
选出 key 分成左右区间 …… 左区间有序,递归右区间。右区间有序,整体有序
递归返回条件:区间只剩一个值或区间不存在

递归的过程虽然图上像是分出来了,其实都是在原数组上走的
和二叉树的前序很像。单趟排是处理根(key),再处理左子树(左区间),右子树(右区间)
void QuickSort(int* a, int left, int right)
{// 递归返回条件if (left >= right) // = 是只剩一个值。> 是没有值return;int begin = left, end = right;int keyi = left;while (left < right){while (left < right && a[right] >= a[keyi]) // 右边找小right--; // 且要防止本来就有序,right 飘出去while (left < right && a[left] <= a[keyi]) // 左边找大left++;Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);keyi = left;// 递归 [begin, keyi-1] keyi [keyi+1, end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}
3. 时间复杂度
理想情况下:(小于)N * logN

N 个数,最终接近满二叉树 ==》logN
当 N = 100W,只需递归 20 层 N = 10亿,递归 30 层 空间消耗不大,每层减的数也不大
最终每一层也还是 N 的量级
最坏:O( N^2 ) 抢救后忽略 已经顺/逆序

递归 N 层,建立 N 个栈帧,会栈溢出

4. 优化(抢救一下)
影响快排性能的是 keyi
keyi 越接近中间的位置,越二分,越接近满二叉树,深度越均匀,效率越高
不是让左边的值做 key ,而是让 key 在最左边的位置
4.1 随机选 key
(生成位置% 区间大小)+ 左边
void QuickSort(int* a, int left, int right)
{// 递归返回条件 ......int begin = left, end = right;// 优化1.随机选 keyint randi = left + (rand() % (left - right));Swap(&a[left], &a[randi]); // 还是让最左边做 keyint keyi = left;while (left < right){ ...... }
}
管你有序无序,都把你变成无序


4.2 三数取中
有序 / 接近有序的情况下,选中间位置做 key 最好。但不一定是有序 / 接近有序
三数取中:选 左右中 3个位置,不是最小,也不是最大的数的位置 两两比较
int GetMidNumi(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]) // mid 不是中间,是最大的。{return left; // 剩下两个:left 和 right 大的就是中间}else{return right;}}else // a[left] > a[mid]{if (a[mid] > a[right]){return mid;}else if (a[left] < a[right]) // mid 是最小的{return left; // 剩下两个:left 和 right 小的就是中间}else{return right;}}
}// 快速排序
void QuickSort(int* a, int left, int right)
{// 递归返回条件 ......int begin = left, end = right;// 优化2.三数取中int midi = GetMidNumi(a, left, right);Swap(&a[midi], &a[left]);int keyi = left;while (left < right){ ...... }
}

二. 挖坑法

 先将第一个数据存放在临时变量 key 中,形成一个坑位
先将第一个数据存放在临时变量 key 中,形成一个坑位
piti 在左,不用想,肯定让 right 先走

right 找到比 key 小的后,把 a[right] 扔到坑里,自己变成坑。left 走。

left 找到比 key 小的后,把 a[left] 扔到坑里,自己变成坑。right 走。
重复以上过程,直到 left 和 right 相遇。相遇点一定是坑,再把 key 扔到坑里
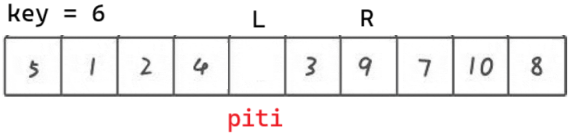



void QuickSort2(int* a, int left, int right)
{// 递归返回条件if (left >= right)return;int begin = left, end = right;// 优化2.三数取中int midi = GetMidNumi(a, left, right);Swap(&a[midi], &a[left]);int piti = left;int key = a[left];while (left < right){while (left < right && a[right] >= key) // 右边找小right--;a[piti] = a[right]; // 扔到左边的坑piti = right; // 自己成新的坑,坑到右边去了while (left < right && a[left] <= key) // 左边找大left++;a[piti] = a[left]; // 扔到右边的坑piti = left; // 自己成新的坑,坑到左边去了}a[piti] = key;// 递归 [begin, piti-1] piti [piti+1, end]QuickSort2(a, begin, piti - 1);QuickSort2(a, piti + 1, end);
}格式优化
如果写单趟,上面的写法就可以
快排的递归框架是不变的,变的是单趟
// Hoare 单趟
int PartSort1(int* a, int left, int right)
{// 三数取中int midi = GetMidNumi(a, left, right);Swap(&a[midi], &a[left]);int keyi = left;while (left < right){while (left < right && a[right] >= a[keyi]) // 右边找小right--;while (left < right && a[left] <= a[keyi]) // 左边找大left++;Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);keyi = left;return keyi;
}// 挖坑 单趟
int PartSort2(int* a, int left, int right)
{// 三数取中int midi = GetMidNumi(a, left, right);Swap(&a[midi], &a[left]);int piti = left;int key = a[left];while (left < right){while (left < right && a[right] >= key) // 右边找小right--;a[piti] = a[right]; // 扔到左边的坑piti = right; // 自己成新的坑,坑到右边去了while (left < right && a[left] <= key) // 左边找大left++;a[piti] = a[left]; // 扔到右边的坑piti = left; // 自己成新的坑,坑到左边去了}a[piti] = key;return piti;
}void QuickSort(int* a, int left, int right)
{if (left >= right)return;int keyi = PartSort2(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}三. 前后指针(最好)
1. cur 找到比 key 小的值,++prev,交换 cur 和 prev 位置的数据,++cur
2. cur 找到比 key 大的值,++cur
把比 key 大的值往右翻,比 key 小的值往左翻









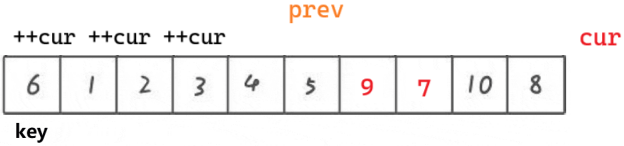

1. prev 要么紧跟着 cur(prev 下一个就是 cur)
2. prev 跟 cur 中间隔着比 key 大的一段值
int PartSort3(int* a, int left, int right)
{// 三数取中int midi = GetMidNumi(a, left, right);Swap(&a[midi], &a[left]);int keyi = left;int prev = left, cur = left + 1;while (cur <= right) // [left, right],所以是 <={if (a[cur] < a[keyi]){++prev;Swap(&a[cur], &a[prev]);++cur;}else{++cur;}}Swap(&a[prev], &a[keyi]);keyi = prev;return keyi;
}void QuickSort(int* a, int left, int right)
{if (left >= right)return;int keyi = PartSort3(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}
while (cur <= right)
{if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[cur], &a[prev]);++cur;
}四. 小区间优化
小区间直接使用直接插入排序
希尔是当数据量特别大时,为了让大数快速往后跳才用
堆排还要建堆,很麻烦
冒泡只有教学意义,现实中几乎没用
选择排序,最好最坏都是 N^2,也没用
上面说递归图看着像二叉树

当区间特别小时,递归的次数会非常多。
光最后一层的递归数,就是总递归数的1/2。倒数第二次占1/4。倒数第三层占1/8
如果小区间直接使用直接插入排序,递归数量会少很多。现实中递归的不均匀,但怎么说也减少了50%的递归数量
void QuickSort(int* a, int left, int right)
{if (left >= right)return;// 小区间优化 - 小区间直接使用插入排序if (right - left + 1 > 10) // [left, right]左闭右闭区间,要 +1{int keyi = PartSort3(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);}else{InsertSort(a + left, right - left + 1);}
}不能写成:InsertSort(a, right - left + 1)
 正确。但如果是这样就出错了:
正确。但如果是这样就出错了:
[ left , right ] 左闭右闭区间,要 +1
五. 改非递归
递归的问题:1. 效率(影响不大) 2. 递归太深,栈溢出。不能调试
递归改非递归:
1. 直接改循环。原来正着走,递归逆着来(简单)。eg:斐波那契数列。
2. 用栈辅助改循环。(难)eg:二叉树
递归里,实际是用下标来 分割子区间
递归里参数条件变化的是什么,栈里面存的就是什么。具体情况具体分析
思路:
1. 栈里面取一段区间,单趟排序
2. 单趟分割子区间入栈
3. 子区间只有一个值、不存在时就不入栈
为了和递归的过程一样,栈里先入右区间,再入左区间。这样就先排好左区间,再排好右区间
在栈里取单个区间时,若想先取左端点、再取右端点,就要先入右端点、再入左端点。
void QuickSortNonR(int* a, int left, int right)
{ST st;STInit(&st);STPush(&st, right);STPush(&st, left);while (!STEmpty(&st)){int begin = STTop(&st);STPop(&st);int end = STTop(&st);STPop(&st);int keyi = PartSort3(a, begin, end);// [begin,keyi-1] keyi [keyi+1, end]if (keyi + 1 < end){STPush(&st, end);STPush(&st, keyi + 1);}if (begin < keyi - 1){STPush(&st, keyi - 1);STPush(&st, begin);}}STDestroy(&st);
}
2 个 if 相当于递归的返回条件
本篇的分享就到这里了,感谢观看,如果对你有帮助,别忘了点赞+收藏+关注。
小编会以自己学习过程中遇到的问题为素材,持续为您推送文章
相关文章:

【数据结构 · 初阶】- 快速排序
目录 一. Hoare 版本 1. 单趟 2. 整体 3. 时间复杂度 4. 优化(抢救一下) 4.1 随机选 key 4.2 三数取中 二. 挖坑法 格式优化 三. 前后指针(最好) 四. 小区间优化 五. 改非递归 快速排序是 Hoare 提出的一种基于二叉树…...

HTTPS和HTTP区别
客户端向服务器发送HTTPS请求。服务器响应并发送其数字证书。客户端通过证书的公钥验证数字签名的有效性,如果有效,客户端生成一个随机的对称密钥。客户端使用公钥对这个对称密钥进行加密,然后将加密后的密钥发送给服务器。服务器使用自己的私…...

自动驾驶中的预测控制算法:用 Python 让无人车更智能
自动驾驶中的预测控制算法:用 Python 让无人车更智能 自动驾驶技术近年来取得了令人惊叹的进步,AI 与边缘计算的结合让车辆能够实时感知环境、规划路径并执行驾驶决策。其中,预测控制(Model Predictive Control,MPC) 作为一种先进的控制算法,凭借其对未来驾驶行为的优化…...

分享一些实用的网址
第一个:视频转化为动图 网址:https://www.freeconvert.com/zh/convert/mp4-to-gif 当然还有很多其他的功能,可以按需选择使用。 第二个:ASCII字符串到16进制在线转换工具 网址 :https://coding.tools/cn/ascii-to-…...
)
打开小程序提示请求失败(小程序页面空白)
1、小程序代码是商城后台下载的还是自己编译的 (1)要是商城后台下载的,检查设置里面的域名是不是https的 (2)要是自己编译的,检查app.js里面的接口域名是不是https的,填了以后有没有保存 注&a…...

Taro 安全区域
目录 一、问题描述 二、问题解决 1、顶部刘海区 2、底部小黑条 一、问题描述 安全区域主要是为了避免刘海屏或底部栏遮挡,而造成的不良显示效果。 本次将针对以下两点进行考量: 1、顶部刘海屏区 2、苹果X底部小黑条 二、问题解决 通过Taro.getS…...

DL00988-稀疏增强数据transformer船舶AIS轨迹预测含完整数据集
提升科研效率,精准预测船舶AIS轨迹!文末有完整获取方式 作为研究生和科研人员,是否在进行船舶轨迹预测时遇到数据稀疏、轨迹复杂等问题?现在,我们为你提供一款基于稀疏增强数据Transformer的船舶AIS轨迹预测工具&#…...
)
重写B站(网页、后端、小程序)
1. 网页端 1.1 框架 Vue ElementUI axios 1.2 框架搭建步骤 搭建Vue 1.3 配置文件 main.js import {createApp} from vue import ElementUi from element-plus import element-plus/dist/index.css; import axios from "axios"; import router from…...

SOPHGO算能科技BM1688内存使用与编解码开发指南
1. BM1688内存分配接口详解 1.1 设备内存分配接口区别 BM1688提供了三个主要的设备内存分配接口,它们的主要区别如下: // 基本设备内存分配接口 void* bm_malloc_device_byte(bm_handle_t handle, unsigned int size);// 指定heap区域的设备内存分配 void*</...

如何使用Antv X6使用拖拽布局?
拖拽效果图 拖拽后 布局预览 官方: X6 图编辑引擎 | AntV 安装依赖 # npm npm install antv/x6 --save npm install antv/x6-plugin-dnd --save npm install antv/x6-plugin-export --save需要引入的代码 import { Graph, Shape } from antv/x6; import { Dnd } …...
升级版)
STM32项目分享:智能家居(机智云)升级版
目录 一、前言 二、项目简介 1.功能详解 2.主要器件 三、原理图设计 四、PCB硬件设计 PCB图 五、程序设计 六、实验效果 七、资料内容 项目分享 一、前言 项目成品图片: 哔哩哔哩视频链接: STM32智能家居(机智云)升级版 (资料…...

Flask-SQLAlchemy核心概念:模型类与数据库表、类属性与表字段、外键与关系映射
前置阅读,关于Flask-SQLAlchemy支持哪些数据库及基本配置,链接:Flask-SQLAlchemy_数据库配置 摘要 本文以一段典型的 SQLAlchemy 代码示例为引入,阐述以下核心概念: 模型类(Model Class) ↔ 数…...
)
算法优选系列(9.BFS 解决拓扑排序)
目录 拓扑排序简介: 编辑 课程表(medium): 课程表II(medium): 火星词典(hard): 拓扑排序简介: 有向无环图(DAG图) 如上图每条边…...

DevExpress Blazor中文教程 - 如何用AI聊天组件构建大型语言模型聊天APP?
DevExpress Blazor UI组件使用了C#为Blazor Server和Blazor WebAssembly创建高影响力的用户体验,这个UI自建库提供了一套全面的原生Blazor UI组件(包括Pivot Grid、调度程序、图表、数据编辑器和报表等)。 AI服务提供各种量身定制的模型来满…...

PHP:经典编程语言在当代Web开发中的新活力
在当今的Web开发领域,新技术和新语言层出不穷,但PHP(超文本预处理器)作为一门经典且功能强大的编程语言,依然在Web开发中占据着重要地位,并不断展现出新的活力。 PHP的历史与现状 PHP诞生于1994年&#x…...

ToDesk云电脑、并行智算云与顺网云AI支持能力深度实测报告
随着AI技术的迅猛发展,云计算平台已成为突破本地硬件限制、实现高效AI计算的关键基础设施。本报告对ToDesk云电脑、并行智算云和顺网云三大主流云平台进行了全面测评,从硬件配置、AI软件兼容性、性能表现、用户体验及成本效益等维度深入分析其AI支持能力…...

javaweb的拦截功能,自动跳转登录页面
我们开发系统时候,肯定希望用户登录后才能进入主页面去访问其他服务,但要是没有拦截功能的话,他就可以直接通过url访问或者post注入攻击了。 因此我们可以通过在后端添加拦截过滤功能把没登录的用户给拦截下来,让他去先登录&#…...
:用户反馈的科学解读与试验驱动迭代——Rally的双向验证方法论)
精益数据分析(75/126):用户反馈的科学解读与试验驱动迭代——Rally的双向验证方法论
精益数据分析(75/126):用户反馈的科学解读与试验驱动迭代——Rally的双向验证方法论 在创业的黏性阶段,用户反馈是优化产品的重要依据,但如何避免被表面反馈误导?如何将反馈转化为可落地的迭代策略&#x…...

轻量级高性能Rust HTTP服务器库Hyperlane,助力现代网络服务开发
轻量级高性能Rust HTTP服务器库Hyperlane,助力现代网络服务开发 Hyperlane是一款专为简化网络服务开发而设计的轻量级、高性能Rust HTTP服务器库。它凭借纯Rust和标准库构建,实现了Windows、Linux和macOS全平台兼容,依托Tokio异步运行时&…...
PCB设计时如何避免EMI)
PCB设计实践(二十四)PCB设计时如何避免EMI
PCB设计中避免电磁干扰(EMI)是一项涉及电路架构、布局布线、材料选择及制造工艺的系统工程。本文从设计原理到工程实践,系统阐述EMI产生机制及综合抑制策略,覆盖高频信号控制、接地优化、屏蔽技术等核心维度,为高密度、…...

VRRP 协议
一、前言 最近被问到一个VRRP的网络协议,一开始我是蒙蔽的状态,至于什么是VRRP,我后面查了一下,因为对于网络这方面我也不是很精通,见谅! VRRP,全称叫虚拟路由冗余协议,是我孤陋寡闻…...

年度工作计划总结述职报告PPT模版一组分享
工作计划总结述职报告PPT模版:工作计划述职报告PPT模版https://pan.quark.cn/s/fba40a5e87da 第一套PPT模版是医院年度工作计划的封面页,有蓝橙配色、医院标题、年度工作计划的大字、英文副标题、汇报人信息和右上角的医院logo区域,右侧还有医…...

【容易坑】mybatis中使用if标签比较两个字符串是否相等
资料都来自于网络,这里只是记录一下,仅供参考 现象 上传参数确实为3,但是到了sql中还是2,很纳闷,确定不是上送参数的问题 问题解决 问题的关键点就在于为啥偏偏是2身上,仔细看一下sql语句,这个…...
:实时数据驱动下的AI架构设计:从流数据到智能决策)
AI与产品架构设计(7):实时数据驱动下的AI架构设计:从流数据到智能决策
实时数据驱动下的AI架构设计:从流数据到智能决策 一、引言:从静态智能到流式智能的革命性跨越 在AI演进的历程中,我们正经历着从"数据仓库时代"向"数据流时代"的范式迁移。传统AI系统依赖的离线批处理模式,…...

测试W5500的第4步_使用ioLibrary库创建UDP客户端和服务器端
从下载网络测试工具,经常会区分UDP客户端和UDP服务器端。其实这么区分,是不正确的。它区分,是因为担心使用的人不会配置,这是它这么设计的原因。 UDP(User Datagram Protocol,用户数据报协议)是一种简单的,无连接的传…...

六台升降台完整的限位保护逻辑
一、限位保护的核心逻辑 以下是实现限位保护功能的关键代码,集成在主控制程序中: // // 限位保护处理 - 集成在主程序中 // FOR i : 1 TO 6 DO// 读取限位状态(从变频器状态字获取)Lifts[i].UpperLimit : (Lifts[i].StatusWord …...

腾讯位置服务地点搜索开发指南
概述 提供多种搜索功能: 指定城市/区域搜索:如在北京搜索景点。新增高级参数:支持获取车站、机场、园区等较大范围地点的子点和出入口热度,辅助用户选择准确目的地。周边搜索:如,搜索颐和园附近半径500米内…...

101个α因子#12
(sign(delta(volume, 1)) * (-1 * delta(close, 1)))worldquant brain平台上调整后的语法: (sign(ts_delta(volume, 1)) * (-1 * ts_delta(close, 1)))这个alpha因子的逻辑可以分为以下几个步骤: 1. 计算成交量的变化方向:sign(ts_delta(vol…...

opencv_version_win32
很多人发了opencv的编译方法,很少见到启动和关闭了那些模块,现在发个WIN64 opencv编译后的信息。 执行opencv_version_win32.exe 因为显卡较老 2060 super, NVIDIA GPU arch: 75 80 86 87 89 90。至于更高的反本没有显卡因此不知道。 BLAS库使用效率较高…...

Flask 路由装饰器:从 URL 到视图函数的优雅映射
前置知识,关于Python装饰器的语法,链接:Python 装饰器:从“语法糖”到“代码神器”的深度解析 1、路由装饰器的功能:给 URL 贴 “功能标签” 在 Flask 开发中,你一定见过这样的代码: from fla…...

动态规划3、悟到核心
题目引入: #include <iostream> #include <queue> #include <vector> #include <tuple> #include <algorithm> #include <cstring> using namespace std;// dp[i]考虑前i家店能收获的最大价值 // 面对第i家店铺,你可…...

VLM-MPC:自动驾驶中模型预测控制器增强视觉-语言模型
《VLM-MPC: Model Predictive Controller Augmented Vision Language Model for Autonomous Driving》2024年8月发表,来自威斯康星大学的论文。 受视觉语言模型(VLM)的紧急推理能力及其提高自动驾驶系统可理解性的潜力的启发,本文…...

HTTP/HTTPS 协议浅解
文章目录 一、HTTP 协议(一)定义(二)特点(三)应用场景(四)优势(五)劣势 二、HTTPS 协议(一)定义(二)特点&…...

Ajax快速入门教程
输入java时,页面并没有刷新但是下面自动联想出了跟java有关的东西,像这种就叫异步交互 它不会妨碍你的输入,同时还能够同步进行对于java相关联想词的推送 发送异步请求需要借助工具axios 引入axios,可以直接在scripts中引入 get和…...
)
如何在Java中处理PDF文档(教程)
在开发文档管理系统、自动化工具或商业应用程序时,Java开发者常需处理PDF文档的编辑需求。无论是添加页面、调整内容尺寸、插入水印还是添加注释,选择一套可靠易用的Java PDF开发工具包至关重要。 JPedal(Java PDF开发工具包)的新…...

springcloud集成seata报错Error creating bean with name ‘globalTransactionScanner‘
1. pom文件引入依赖 <!-- seata --><dependency><groupId>com.alibaba.cloud</groupId><artifactId>spring-cloud-starter-alibaba-seata</artifactId></dependency> 2. 报错 3. 在启动配置中添加一行配置: --add-opensjava.base/j…...

使用 OpenCV 实现哈哈镜效果:让图像“扭曲起来”!
在计算机视觉和图像处理领域,OpenCV 提供了非常强大的图像几何变换能力,不仅可以用于纠正图像,还能制造各种“有趣”的视觉效果。今天,我们就来实现一个经典的“哈哈镜”效果,让图像像在游乐园里一样被拉伸、压缩、扭曲…...

pikachu靶场 暴力破解
学习中参考的博客如下 pikachu靶场暴力破解专题-CSDN博客 1,基于表单的暴力破解 出现了一个登录页面 解题步骤:抓包,发到bp里,右键发到Intruder,因为有两个位置要爆破,所以选择集群炸弹攻击ÿ…...

鸿蒙开发:应用上架第三篇,配置签名信息打出上架包
前言 本文基于Api13 经过前面两篇文章,我们获取到了密钥和证书请求文件以及最终的发布证书和发布证书Profile文件,可以说,所有的签名信息文件,我们都已经完成了,正所谓,万事俱备只欠东风,这篇文…...

基于R语言的贝叶斯网络模型实践技术应用:开启科研新视角
在现代科研领域,变量间的因果关系推断是生态学、环境科学、医学等多学科研究的核心问题。然而,传统的统计学方法往往只能揭示变量间的相关关系,而非因果关系。贝叶斯网络作为一种结合图论与统计学理论的新型模型,不仅能够统合多种…...

第五章 GPT模块配置
由于GPT配置需要和Irq和Mcu进行配合设置(GPT可以由芯片外设中的GTM和GPT12实现,这次是以GTM为实现)。 1 GTM外设时钟配置 首先需要对MCU组件进行配置,配置GTM的时钟,需要参照GTM的CMU时钟树。 下图时钟树的CLS0_CLK为MCU(McuClockSettingConfig_0中的 McuSTMFrequency )f…...

虚拟机NAT模式获取不到ip
虚拟机NAT模式获取不到ip 如图所示 解决方案: 先查看NetworkManager是否启动 systemctl status NetworkManager如果没启动就启动一遍 使用DHCP手动获取一遍ip sudo dhclient ens33成功得到ip 这是后遇到了另一个问题,ip释放后,不能自动…...

Docker的网络介绍
网络简单介绍 在介绍 Docker 的网络模式之前,先简单说下我们在使用 Vmware 虚拟机中的网络模式,形成对比,更好理解。 1、Vmware 中的网络模式 1.1、VMnet0(桥接模式) 虚拟机通过宿主机的物理网卡直接连接到外部网络…...

Nginx负载均衡配置详解
在Nginx中配置负载均衡主要通过 upstream 模块实现,结合反向代理将请求分发到多个后端服务器。以下是详细配置步骤和案例解析: 一、基础配置 1. 配置语法 http {upstream backend_servers {# 负载均衡策略server backend1.example.com;server backend2.example.com;server …...

关于 Web 漏洞原理与利用:4. 文件上传漏洞
定义:文件上传漏洞是指应用程序允许用户上传文件,但没有严格校验上传文件的类型、内容、路径等属性,导致攻击者可以上传并执行恶意代码。 绕过方式: 前端绕过 1. 前端限制的原理 前端限制上传文件类型的常见方式有三种…...
python爬虫--selenium)
(6)python爬虫--selenium
文章目录 前言一、初识selenium二、安装selenium2.1 查看chrome版本并禁止chrome自动更新2.1.1 查看chrome版本2.1.2 禁止chrome更新自动更新 2.2 安装对应版本的驱动程序2.3安装selenium包 三、selenium关于浏览器的使用3.1 创建浏览器、设置、打开3.2 打开/关闭网页及浏览器3…...

MCU 上电不启动的常见原因分析与排查思路
在开发过程中,“MCU 上电不运行”是我们经常遇到的问题之一。但客户对此类问题的描述往往较为模糊,仅简单表示“产品不工作”或“怀疑 MCU 没有运行”,这给我们现场排查带来了较大的挑战。即便工程师到达现场,往往也无法迅速定位问…...

Spark Core 源码关键环节的深度解析
以下是对 Spark Core 源码关键环节的深度解析,包括核心组件启动与调度机制、Shuffle与调度系统、RDD高级机制。每个环节都细化到具体方法、逻辑、源码片段,附有流程图思路与速记口诀,便于记忆和理解。 一、核心组件启动与调度机制 1. RpcEnv…...

net Core》》包与库 LibMan、NPM
LibMan 资料 NPM 资料 在 Visual Studio 中使用 npm package.json 保存之后 vs会自动下载的。 注意:如果您没有看到 node_modules 文件夹,请确保在 Visual Studio 解决方案资源管理器中启用了“显示所有文件”选项 要卸载该库,您只需从 …...

数学建模,机器决策人建模
目录 数学建模 微分方程 动态系统建模 时间序列分析 概述 指数衰减 随机漂移 总结 曲线拟合 最优化方法 梯度下降法 概率建模(如贝叶斯建模、马尔可夫过程、MDP/POMDP) 等 贝叶斯建模 贝叶斯定理 优势 马尔可夫过程 马尔可夫过程的分类…...
