当前位置： 首页 > news >正文

非线性1 修改

news 来源：原创 2025/6/3 20:09:20

第一章为读者介绍了非线性动力学与混沌理论的基本概念、发展历史以及应用领域。

1.1 动力学简史：

  • 从牛顿力学开始，介绍动力学作为物理学分支的发展历程。
  • 重点介绍了庞加莱对混沌现象的早期探索，以及20世纪60年代洛伦兹方程的发现，标志着混沌理论的诞生，并回顾了20世纪70年代混沌理论的快速发展。
  • 洛伦兹发现了混沌的特定结构：
    在这里插入图片描述

1.2 非线性的重要性：

  • 消除时间依赖：增加一个维度

  • 在这里插入图片描述
    x ′ ′ → x 1 , x ′ → x 2 , t → x 3 x'' \rightarrow x_1 , x' \rightarrow x_2 , t\rightarrow x_3 x′′→x1​,x′→x2​,t→x3​
    在这里插入图片描述

  • 强调非线性系统难以求解：因为叠加原理失效

  • 但几何方法可以帮助我们理解其定性特征。

  • 相空间：
    相空间

第二章 直线上的流

2.1 几何的思维方式：

  • 系统x’ = sin(x)，解：
    在这里插入图片描述
    在x轴上表示出x的速度向量：
    向量场
    在这里插入图片描述
    x ∈ ( π / 4 , π ) x \in (\pi/4,\pi) x∈(π/4,π):x-t图
    在这里插入图片描述

  • 不动点的概念: x ˙ = 0 \dot{x}=0 x˙=0，表示没有流动

  • 区分稳定不动点（吸引子、汇）和不稳定不动点（排斥子、源）：在这里插入图片描述
    在这里，实轴就是相空间

2.2 不动点与稳定性：

  • 相点：放置在初始条件 x 0 x_0 x0​的粒子
  • 轨迹：相点随时间根据X（t）运动
  • 相图的概念：所有不同的定性轨迹
    在这里插入图片描述
    2.3 种群增长：
    公式：

在这里插入图片描述

  • 图像：

在这里插入图片描述
N<K增加，且先慢后快后慢

2.4 线性稳定性分析：

  • 线性稳定性分析：判断不动点x*的稳定性

  • 给一个小扰动 η \eta η: η ( t ) = x ( t ) − x ∗ \eta(t)=x(t)-x^* η(t)=x(t)−x∗
    在这里插入图片描述
    在不动点处， x ˙ = f ( x ∗ ) = 0 \dot{x}=f(x^*)=0 x˙=f(x∗)=0,要观察一段时间后这个扰动是变大还是变小
    在这里插入图片描述
    线性化：
    得到 η ˙ ≈ η \dot{\eta}\approx\eta η˙​≈η f ′ ( x ∗ ) f'(x^*) f′(x∗)

    最终 η = e f ′ ( x ∗ ) + C \eta=e^{f'(x^*)+C} η=ef′(x∗)+C，指数律增减

  • 判断不动点的稳定性：不动点处的斜率f’(x*)

  • 斜率>0:不稳定，

  • 斜率<0:稳定，

  • 斜率=0：不能忽略O(η²)

  • 特征时间尺度：1/f’(x*)：x(t)在t时间发生较大变化所需的时间

2.5 存在性与唯一性：

  • 存在性与唯一性定理：在这里插入图片描述在这里插入图片描述

2.6 振动的不可能性：

  • 一维自治系统中振动现象的不可能性： x ˙ = f ( x ) \dot{x}=f(x) x˙=f(x)无周期解
    *一个点不可能有两个速度

2.7 势：

  • 将一阶系统 x ˙ = f ( x ) \dot{x}=f(x) x˙=f(x)可视化
  • 势的概念： f ( x ) = − d V d x f(x)=-\frac{dV}{dx} f(x)=−dxdV​
  • 与向量场之间的关系:两边对x求导：f’=-V’’
  • V的局部最小值=>稳定不动点，局部最大值=>不稳定
  • 实例： x ˙ = − x \dot{x}=-x x˙=−x
    d V / d x = x 2 / 2 + C dV/dx=x^2/2+C dV/dx=x2/2+C

在这里插入图片描述

2.8 利用计算机解方程：

  • 显式欧拉法在这里插入图片描述

  • 改进欧拉法在这里插入图片描述

  • 龙格库塔法（四阶）

  • 在这里插入图片描述

第三章——分岔。

分岔是指当参数变化时，系统的动力学行为发生定性改变的过程：
例如不动点的出现、消失或稳定性改变。
3.1 鞍-结分岔：

  • 标准形式： x ′ = r + x 2 x' = r + x^2 x′=r+x2:在这里插入图片描述
    r-x图
    在这里插入图片描述
    变体： x ˙ = r − x − e − x \dot{x}=r-x-e^{-x} x˙=r−x−e−x在这里插入图片描述
    标准形式： x ˙ = r ± x 2 \dot{x}=r\pm x^2 x˙=r±x2

3.2 跨临界分岔

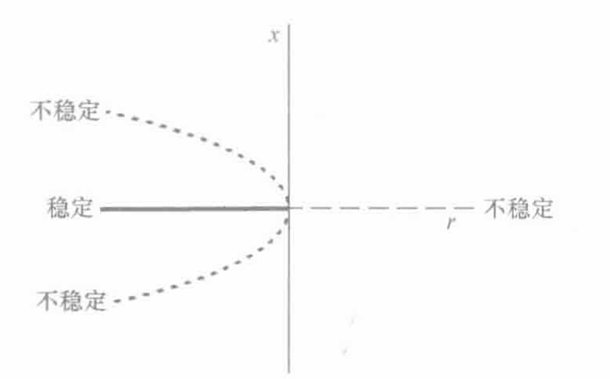
  • 定义：跨临界分岔是指不动点的稳定性发生改变，但不动点本身不消失的现象。
  • 标准形式： x ′ = r x − x 2 x' = rx-x^2 x′=rx−x2
  • 稳定性的交换：在这里插入图片描述
    分叉曲线：
    在这里插入图片描述
  • 变体： x ˙ = r ln ⁡ x + x − 1 \dot{x}=r\ln x+x-1 x˙=rlnx+x−1在x=1附近的分岔：
  • 变换：u=x-1在这里插入图片描述

3.3 激光阈值

  • 激光阈值的物理机制:当泵浦强度超过阈值时，系统会发生跨临界分岔，从而产生激光。

  • 在这里插入图片描述
    在这里插入图片描述
    分岔图：N0=k/G处发生跨临界分叉在这里插入图片描述

  • N 0 / G N_0/G N0​/G为激光阈值

3.4 叉式分岔

  • 叉式分岔是指具有对称性的系统，其不动点成对出现或消失的现象。
  • 超临界叉式分岔和亚临界叉式分岔：分别对应着不动点在分岔后不消失和消失的情况。
  • 在这里插入图片描述
  • 3.4.1 超临界叉式分岔

  • 标准形式： x ′ = r x − x 3 x' = rx - x^3 x′=rx−x3

  • 当变换 x → − x x\rightarrow -x x→−x时，方程不变——向量场等变/对称

  • 向量场：在这里插入图片描述
    分岔图：
    在这里插入图片描述

  • 变体： x ˙ = − x + β tanh ⁡ x \dot{x}=-x+\beta \tanh x x˙=−x+βtanhx

  • 向量场：

  • 在这里插入图片描述

  • 分岔图： β = tanh ⁡ x / x \beta=\tanh x/x β=tanhx/x
    在这里插入图片描述

  • 3.4.2亚临界叉式分岔

  • 一个示例： x ′ = r x + x 3 x' = rx +x^3 x′=rx+x3

  • 分岔图：在这里插入图片描述
    上述系统容易产生爆炸：即有限时间内x(t)->无穷
    标准形式 x ′ = r x + x 3 − x 5 x' = rx +x^3-x^5 x′=rx+x3−x5（为了对称，不能加x^4）在这里插入图片描述

  • 跳跃：r=0时，跳跃到大振幅分支

  • 滞后：减小r也不能回到原点了，除非减小到r_s
    在这里插入图片描述

3.5 旋转环上的过阻尼球

  • 介绍了旋转环上的过阻尼球问题，并建立了一个简化的模型，解释了小球在旋转环上的运动。
  • 在这里插入图片描述
    在这里插入图片描述

顶部：φ=π，底部：=0

在这里插入图片描述

  • 发现当旋转环的角速度超过某个临界值时，系统会发生超临界叉式分岔，从而出现三个平衡点。
  • 无量纲化、无量纲组：

3.6 不完美分岔与灾变

  • 定义：不完美分岔是指当存在对称性的近似时，系统会发生分岔的现象。
  • 灾变：当参数变化时，系统状态会跨越某个临界值，之后发生不连续的改变。
  • 标准形式：x’ = r - x^3 + x
  • 分析方法：通过观察函数 f(x) 和 x 轴的交点，以及它们在分岔点附近的泰勒展开式，可以判断分岔的发生和不动点的稳定性。
  • 应用：昆虫爆发、斜线上的小球等。
    3.7 昆虫爆发
  • 介绍了云杉蚜虫爆发模型，解释了蚜虫数目突然增加的现象。
  • 通过无量纲分析，将模型简化为一维系统，并分析其不动点的分岔行为。
  • 发现当天敌捕食作用增强时，系统会发生鞍-结分岔，从而导致蚜虫爆发。
  • 该模型展示了分岔在生态学中的应用，以及如何通过参数变化来预测系统的行为。
    本章通过多种类型的分岔，以及它们在科学和工程中的应用，展示了分岔的多样性和重要性。分岔是理解非线性系统行为的关键，它在物理学、生物学、工程学等多个领域都有着广泛的应用。

3.2 跨临界分岔：

  • 介绍跨临界分岔的概念，并以x’ = r(1 - x)为例，说明其发生机制和特征。
  • 解释跨临界分岔的标准形式，并介绍其绘图方法。
  • 通过实例，说明跨临界分岔在激光物理中的应用。
    3.3 激光阈值：
  • 介绍激光物理背景，并介绍一个简化激光模型。
  • 利用向量场和相图，分析激光阈值现象，并解释其物理意义。
  • 讨论该模型的局限性，并引出更复杂的激光模型。
    3.4 叉式分岔：
  • 介绍叉式分岔的概念，并区分超临界叉式分岔和亚临界叉式分岔。
  • 以x’ = r - x^3为例，说明超临界叉式分岔的发生机制和特征。
  • 解释超临界叉式分岔的标准形式，并介绍其绘图方法。
  • 通过实例，说明叉式分岔在物理和生物学中的应用。
    3.5 旋转环上的过阻尼球：
  • 介绍旋转环上过阻尼球的问题，并推导其动力学方程。
  • 利用向量场和相图，分析过阻尼球在不同参数下的运动状态。
  • 引入量纲分析和尺度化的概念，解释将二阶系统近似为一阶系统的可行性。
  • 讨论该问题的奇异极限性质，并引出奇异摄动理论。
    3.6 不完美分岔与灾变：
  • 介绍不完美分岔的概念，并以x’ = y^3 - xy为例，说明其发生机制和特征。
  • 解释尖点灾变的概念，并介绍其绘图方法。
  • 通过实例，说明不完美分岔和尖点灾变在力学和生物学中的应用。
    3.7 昆虫爆发：
  • 介绍云杉蚜虫爆发模型，并解释其物理背景和参数含义。
  • 利用向量场和相图，分析蚜虫数目随时间变化的动力学特征。
  • 讨论模型的近似方法和参数估计，并解释爆发现象的物理意义。
    3.8 本章总结：
  • 本章深入探讨了分岔现象，并介绍其在科学中的应用。
  • 介绍了鞍-结分岔、跨临界分岔、叉式分岔等不同类型的分岔，并解释其发生机制和特征。
  • 通过实例，展示了分岔现象在物理、生物学等领域的应用，并说明其对理解自然界复杂现象的重要性。
    第三章的核心观点在于：
  • 分岔是描述系统行为随参数变化而发生定性改变的关键概念。
  • 分岔现象在自然界中普遍存在，并具有重要的科学意义。
  • 几何方法可以帮助我们直观地理解分岔现象，并预测其发生规律。
  • 分岔现象在多个领域具有广泛的应用，例如激光物理、力学、生物学等。

相关文章：

非线性1 修改

第一章为读者介绍了非线性动力学与混沌理论的基本概念、发展历史以及应用领域。 1.1 动力学简史&#xff1a; 从牛顿力学开始&#xff0c;介绍动力学作为物理学分支的发展历程。重点介绍了庞加莱对混沌现象的早期探索&#xff0c;以及20世纪60年代洛伦兹方程的发现&#xff0…...

编程日记 2025/6/3 20:09:20

系统性能不达标，如何提升用户体验？

当系统性能不达标时&#xff0c;要想有效提升用户体验&#xff0c;必须从性能优化、前后端协同、用户感知改善、监控预警机制四个关键维度切入。其中&#xff0c;性能优化是最直接有效的策略&#xff0c;它通过代码优化、资源压缩、缓存机制、CDN加速等手段&#xff0c;显著提升…...

编程日记 2025/5/26 9:16:57

【Linux】进程的基本概念

目录 概念描述进程-PCB如何查看进程通过系统目录进行查看通过ps指令进行查看 通过系统调用获取进程的PID和PPID(进程标⽰符)通过系统调用创建子进程通过一段代码来介绍fork为什么要有子进程&#xff1f;fork为什么给子进程返回0&#xff0c;给父进程返回子进程的PIDfork函数到底…...

编程日记 2025/5/19 5:47:43

mongodb管理工具的使用

环境&#xff1a; 远程服务器的操作系统&#xff1a;centOS stream 9; mongoDB version:8.0; 本地电脑 navicat premium 17.2 ; 宝塔上安装了mongoDB 目的&#xff1a;通过本地的navicat链接mongoDB,如何打通链接&#xff0c;分2步&#xff1a; 第一步&#xff1a;宝塔-&…...

编程日记 2025/5/31 10:42:59

面试中的线程题

原文链接&#xff1a;线程题大全 Java 并发库同步辅助类 CountDownLatch 工作机制&#xff1a;初始化一个计数器&#xff0c;此计数器的值表示需要等待的事件数量。 提供了两个主要方法&#xff1a; await()&#xff1a;当一个线程调用此方法时&#xff0c;它将阻塞&#…...

编程日记 2025/5/26 7:16:30

计算机系统的层次结构

计算机系统的层次结构 一, 计算机系统的层次结构的定义 计算机的一个赢软件组成的综合体. 因为面对的应用范围越来越广, 所以必须有复杂的系统软件和硬件的支持. 软/硬件的设计者和使用者从不同的角度, 不同的语言来对待同一个计算机系统, 因此他们看到的计算机系统的属性对计…...

编程日记 2025/5/28 13:24:39

[特殊字符] SSL/TLS 中的密钥协商流程笔记

✅ 背景说明&#xff1a; SSL/TLS 为了确保通信保密性&#xff0c;结合使用了&#xff1a; 非对称加密&#xff08;用于密钥交换&#xff09; 对称加密&#xff08;用于数据加密&#xff09; &#x1f501; 客户端主导密钥协商的完整流程如下&#xff1a; 1️⃣ 客户端发起…...

编程日记 2025/5/22 3:06:09

多模态大语言模型arxiv论文略读（八十一）

What is the Visual Cognition Gap between Humans and Multimodal LLMs? ➡️ 论文标题&#xff1a;What is the Visual Cognition Gap between Humans and Multimodal LLMs? ➡️ 论文作者&#xff1a;Xu Cao, Bolin Lai, Wenqian Ye, Yunsheng Ma, Joerg Heintz, Jintai …...

编程日记 2025/5/28 14:40:51

SpringBoot（一）--- Maven基础

目录 前言 一、初始Maven 1.依赖管理 2.项目构建 3.统一项目结构 二、IDEA集成Maven 1.Maven安装 2.创建Maven项目 2.1全局设置 2.2 创建SpringBoot项目 2.3 常见问题 三、单元测试 1.JUnit入门 2.断言 前言 Maven 是一款用于管理和构建Java项目的工具&#xff…...

编程日记 2025/5/29 9:29:42

如何使用WordPress创建美食博客

不管你是否意识到&#xff0c;食物是我们生活的核心。有些人将其用作燃料&#xff0c;而另一些人则将食谱作为一种艺术形式呈现。如果您属于后者&#xff0c;并且想创建一个美食博客来分享您的热情&#xff0c;那么WordPress是一个顶级平台。 几乎每个话题都有一个博客利基&am…...

编程日记 2025/5/23 19:16:48

SAP集团内部公司间交易自动开票

SAP集团内部公司间交易自动开票(非STO/EDI模式) 集团内部公司间采购与销售业务&#xff0c;在确认相应单据无误后&#xff0c;为减少人工开票业务&#xff0c; 可以用系统标准功能来实现自动开票。 1.采购发票自动开票(ERS) T-CODE:BP,勾选“基于收货的发票校验”、“自动G…...

编程日记 2025/5/25 10:30:33

代码审计-php框架开发，实战tp项目，打击微交易，源码获取，扩大战果

实战&#xff0c;不安全写法引发的注入 这个bc靶场源码没有&#xff0c;看老师演示 打开很明显的tp框架源码 拿到tp框架之后第一步&#xff0c;搜索版本信息5.0.5 两个思路 1.代码的不安全写法 2.版本自身存在的漏洞 全局搜索where看看也没有不安全的 哎&#xff1f;&…...

编程日记 2025/5/26 14:45:05

Atcoder Beginner Contest 406

比赛链接&#xff1a;ABC406 A - Not Acceptable 将小时转换成分钟直接进行判断。 时间复杂度&#xff1a; O ( 1 ) O(1) O(1)。 #include <bits/stdc.h> using namespace std;int main() {ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);int a,…...

编程日记 2025/5/29 11:59:52

02 K8s双主安装

00 前提准备 # 设置好主机名并添加hosts解析主机名IP地址身份master01172.2.25.50主Mastermaster02172.2.25.51备Masternode01172.2.25.52节点1node02172.2.25.53节点2node03172.2.25.54节点3 01 使用脚本安装Docker # Docker脚本文件 https://node-siyuan.oss-cn-beijing.a…...

编程日记 2025/6/1 16:26:11

分别用 语言模型雏形N-Gram 和 文本表示BoW词袋 来实现文本情绪分类

语言模型的雏形 N-Gram 和简单文本表示 Bag-of-Words 语言表示模型简介 (1) Bag-of-Words (BoW) 是什么&#xff1f; *定义&#xff1a;将文本表示为词频向量&#xff0c;忽略词序和语法&#xff0c;仅记录每个词的出现次数。 **示例&#xff1a; 句子1&#xff1a;I love …...

编程日记 2025/6/1 8:50:36

2_Spring【IOC容器中获取组件Bean】

Spring中IOC容器中获取组件Bean 实体类 //接口 public interface TestDemo {public void doSomething(); } // 实现类 public class HappyComponent implements TestDemo {public void doSomething() {System.out.println("HappyComponent is doing something...")…...

编程日记 2025/5/26 17:16:24

一次页面假死分析

现象&#xff1a;系统的几个功能若干次切换&#xff0c;页面假死&#xff0c;无反应 上图&#xff0c;不是每次切换都假死&#xff0c;但非常容易重现&#xff0c;每次页面假死都在getValidatorJSONInfo这个调用后 getValidatorJSONInfo调用已返回&#xff0c;但返回内容页面挂…...

编程日记 2025/5/22 19:48:20

WPS多级标题编号以及样式控制

WPS多级标题编号以及样式控制 上一篇&#xff1a;WPS自动生成图表目录以及样式控制 阅读提示&#xff1a;请先阅读完本篇内容再操作&#xff0c;避免出现其他错误。 初始样式&#xff1a; 1.1 步骤演示 说明&#xff1a;以3级目录为例 标题1样式&#xff1a;黑体&#xff0c;…...

编程日记 2025/5/29 3:24:48

方差是什么？

一、方差是什么？ 方差（Variance）是概率论和统计学中衡量数据离散程度（即数据与平均值的偏离程度）的核心指标。 通俗理解：方差越大，数据越“分散”“波动大”；方差越小，数据越“集中”“稳定”。 二、方差的公式（以样本数据为例） 计算步骤： 第一步：求平均值 ( …...

编程日记 2025/5/28 16:21:24

Java核心API实战：从字符串到多线程全解析

Java常用API详解与代码实践 一、字符串处理类 1. String类 // 字符串基础操作 String str "Hello,Java!"; System.out.println(str.substring(7)); // 输出"Java!" System.out.println(str.indexOf("Java")); // 输出7// 正则表达式匹配 Str…...

编程日记 2025/5/28 8:14:12

低代码AI开发新趋势：Dify平台化开发实战

在人工智能快速发展的今天&#xff0c;AI应用的开发方式也在不断演变。从传统的手写代码到如今的低代码甚至零代码开发&#xff0c;技术的进步让更多的非专业开发者也能轻松上手。本文将带你走进Dify平台化开发的世界&#xff0c;探索如何通过这一强大的低代码AI开发平台&#…...

编程日记 2025/5/22 19:53:29

基于First Order Motion与TTS的AI虚拟主播系统全流程实现教程

前言&#xff1a;多模态虚拟主播的技术革命 在AI内容生成领域&#xff0c;虚拟主播技术正经历从2D到3D、从固定模板到个性化定制的跨越式发展。本文将深入解析如何通过Python技术栈构建支持形象定制与声音克隆的AI虚拟主播系统&#xff0c;涵盖从人脸建模到多模态融合的全流程…...

编程日记 2025/5/26 13:57:24

中科院自动化研究所通用空中任务无人机！基于大模型的通用任务执行与自主飞行

作者&#xff1a; Ji Zhao and Xiao Lin 单位&#xff1a;中科院自动化研究所 论文标题&#xff1a;General-Purpose Aerial Intelligent Agents Empowered by Large Language Models 论文链接&#xff1a;https://arxiv.org/pdf/2503.08302 主要贡献 硬件-软件协同设计框…...

编程日记 2025/5/26 10:41:46

DOM知识点

DOM&#xff08;Document Object Model&#xff09;即文档对象模型&#xff0c;是用于表示和操作HTML、XML文档的编程接口。以下是关于DOM的一些知识点总结&#xff1a; 基本概念 • DOM将文档解析为一个由节点&#xff08;Node&#xff09;组成的树形结构&#xff0c;每个节…...

编程日记 2025/6/1 8:10:26

设备预测性维护的停机时间革命：中讯烛龙如何用AI重构工业设备管理范式

在工业4.0的智能化浪潮中&#xff0c;非计划停机每年吞噬企业3%-8%的产值。中讯烛龙预测性维护系统通过多模态感知矩阵分布式智能体的创新架构&#xff0c;实现设备健康管理的范式跃迁&#xff0c;帮助制造企业将停机时间压缩70%以上。本文将深度解析技术实现路径与行业级实践方…...

编程日记 2025/5/29 17:29:01

JMeter 教程：使用 HTTP 请求的参数列表发送 POST 请求（form 表单格式）

目录 ✅ 教程目的 &#x1f6e0;️ 准备工作 &#x1f4c4; 操作步骤 第一步&#xff1a;新建测试计划 第二步&#xff1a;添加 HTTP 请求 第三步&#xff1a;添加参数列表&#xff08;表单参数&#xff09; 第四步&#xff1a;添加结果查看器 第五步&#xff1a;运行测…...

编程日记 2025/6/1 10:06:14

**HTTP/HTTPS基础** - URL结构(协议、域名、端口、路径、参数、锚点) - 请求方法(GET、POST) - 请求头/响应头 - 状态码含义

# HTTP/HTTPS基础知识点详解 ## 1. URL结构 ### 协议部分 - http:// - 超文本传输协议&#xff0c;明文传输 - https:// - 安全的超文本传输协议&#xff0c;使用SSL/TLS加密 - 爬虫注意点&#xff1a;HTTPS网站有TLS指纹(JA3指纹)&#xff0c;可被用于检测爬虫 ### 域名部分…...

编程日记 2025/5/27 8:32:31

2025抓包工具Reqable手机抓包HTTPS亲测简单好用-快速跑通

前言 自安卓7.0高版本系统不在信任用户证书&#xff0c;https抓包方式市面查找方法太过复杂手机要root等&#xff0c;前置条件要求太高太复杂&#xff0c;看的头痛&#xff0c;今天一台电脑按步骤操作完即可抓包https,给大家搞定抓包https问题。支持直接编辑修改请求参…...

编程日记 2025/5/29 16:00:22

大模型在胫骨平台骨折预测及治疗方案制定中的应用研究

目录 一、引言 1.1 研究背景与目的 1.2 国内外研究现状 1.3 研究方法和创新点 二、大模型预测胫骨平台骨折的原理和方法 2.1 相关大模型介绍 2.2 数据收集与预处理 2.3 模型训练与优化 2.4 模型评估指标 三、术前预测与手术方案制定 3.1 骨折类型和严重程度预测 3.…...

编程日记 2025/5/29 13:09:26

AI图像处理之ComfyUI节点（二）

一、Load Checkpoint节点 功能&#xff1a;用于加载预训练的大模型&#xff0c;如Stable Diffusion等 参数&#xff1a; chechkpoint&#xff1a;选择加载的模型文件&#xff08;.ckpt或.satetensors格式&#xff09; MODEL&#xff1a;输出用于图像扩散预测的UNet模型 CLIP&…...

编程日记 2025/5/29 12:20:03

异常日志规范

目录 一、错误码 二、异常处理 三、日志规约 一、错误码 强制&#xff1a; 1、错误码的制订原则&#xff1a;快速溯源、沟通标准化。 1&#xff09;错误码必须能够快速知晓错误来源&#xff0c;可快速判断是谁的问题。 2&#xff09;错误码必须能够清晰地比对&#xff08;…...

编程日记 2025/5/29 13:35:36

pycharm连接github（详细步骤）

【前提&#xff1a;菜鸟学习的记录过程&#xff0c;如果有不足之处&#xff0c;还请各位大佬大神们指教&#xff08;感谢&#xff09;】 1.先安装git 没有安装git的小伙伴&#xff0c;看上一篇安装git的文章。 安装git&#xff0c;2.49.0版本-CSDN博客 打开cmd&#xff08;…...

编程日记 2025/5/31 23:11:31

UESplineThicken节点

SplineThicken 函数用来使非常薄的多边形在渲染时显示为略厚。对于线缆、头发、草和其他此类对象&#xff0c;这种效果非常理想。 SplineThicken节点 该节点始终朝向摄像机 可以控制模型前后宽度 可以连接到wpo上制作特效效果 参考链接 https://dev.epicgames.com/document…...

编程日记 2025/5/29 16:59:14

【C++】map和set的使用

&#x1f4cc; 个人主页&#xff1a; 孙同学_ &#x1f527; 文章专栏&#xff1a;C &#x1f4a1; 关注我&#xff0c;分享经验&#xff0c;助你少走弯路 文章目录 1. 序列式容器和关联式容器1.1 序列式容器1.2 关联式容器 2. set系列的使用2.1 set和multiset的参考文档2.2 se…...

编程日记 2025/5/19 5:40:11

MCP实战：在扣子空间用扣子工作流MCP，一句话生成儿童故事rap视频

扣子最近迎来重要更新&#xff0c;支持将扣子工作流一键发布成MCP&#xff0c;在扣子空间里使用。 这个功能非常有用&#xff0c;因为我有很多业务工作流是在扣子平台上做的&#xff0c;两者打通之后&#xff0c;就可以在扣子空间里直接通过对话方式调用扣子工作流了&#xff0…...

编程日记 2025/5/30 9:10:40

c/c++的opencv直方图初识

C/C OpenCV中的图像直方图&#xff1a;零基础入门指南 &#x1f4ca; 大家好&#xff01;今天我们来聊聊图像处理中一个非常基础且重要的概念——直方图(Histogram)。如果你是OpenCV新手&#xff0c;或者对直方图感觉有点迷糊&#xff0c;别担心&#xff0c;这篇文章会用最简单…...

编程日记 2025/5/27 14:12:58

Spring Boot 与 RabbitMQ 的深度集成实践（一）

引言 ** 在当今的分布式系统架构中&#xff0c;随着业务复杂度的不断提升以及系统规模的持续扩张&#xff0c;如何实现系统组件之间高效、可靠的通信成为了关键问题。消息队列作为一种重要的中间件技术&#xff0c;应运而生并发挥着举足轻重的作用。 消息队列的核心价值在于其…...

编程日记 2025/5/28 7:38:08

Android动态音频柱状图可视化解析：从原理到实现

Android动态音频柱状图可视化解析：从原理到实现 一、整体架构设计二、核心组件设计三、核心代码实现四、交互设计与用户体验五、性能优化与问题解决一、整体架构设计 Android动态音频柱状图可视化解析 在移动应用开发中，音频可视化是增强用户体验的重要手段。无论是音乐播放器…...

编程日记 2025/5/29 23:02:59

vue3大事件项目

这周写完了vue3的大事件项目&#xff0c;从中学到了很多东西&#xff0c;并且解決了一部分bug&#xff0c;現在就和大家分享一下我遇到的问题并且是如何解決的 1. QuillEditor 的 v-model 用法错误 先讲一下quilleditor富文本的基本使用方法&#xff1a; 1.安裝quill依賴&am…...

编程日记 2025/6/1 7:15:08

MapReduce-WordCount实现按照value降序排序、字符小写、识别不同标点

要求&#xff1a; 输入文件的按照空格、逗号、点号、双引号等分词 输入文件的大写字母全部换成小写 文件输出要求按照value值降序排序 Hadoop给的wordcount示例代码以及代码理解 基于map reduce的word count个人理解&#xff1a;输入的文件经过map reduce框架处理后&#…...

编程日记 2025/5/25 12:20:10

c++线段树之单点修改区间最大子段和-----P4513 小白逛公园

题目大意 单点修改查询区间最大字段和 解题思路 如果线段树节点存储的是‘区间最大子段和’&#xff0c;如何合并&#xff1f; 简单的加法或求极值都不行&#xff0c;仔细分析可得&#xff0c;父节点最大字段和可能为&#xff1a; 左子树最大子段和右子树最大子段和左子树最…...

编程日记 2025/5/29 13:52:47

[Java实战]Spring Boot整合Elasticsearch（二十六）

[Java实战]Spring Boot整合Elasticsearch&#xff08;二十六&#xff09; 摘要&#xff1a;本文通过完整的实战演示&#xff0c;详细讲解如何在Spring Boot项目中整合Elasticsearch&#xff0c;实现数据的存储、检索和复杂查询功能。包含版本适配方案、Spring Data Elasticsea…...

编程日记 2025/5/29 19:30:58

【深度学习新浪潮】大模型在哪些垂域已经有比较好的落地？

AI大模型在多个垂直领域已实现显著落地，以下结合可验证案例与行业数据展开说明： 一、医疗健康：精准诊断与个性化治疗 呼吸系统疾病诊断 国家呼吸医学中心研发的LungDiag模型，基于公开临床数据集训练，在预印本研究中对肺炎、肺癌等10种疾病的辅助诊断准确率达92%。医联Med…...

编程日记 2025/5/28 8:12:36

软件测试全攻略：从概念到实践

目录 测试指南针--概念篇 1. 什么是软件测试&#xff1f; 2. 软件测试和软件开发的关系是什么&#xff1f; 3. 测试需要哪些能力&#xff1f; 4. 测试流程是什么样的&#xff1f; 5. 什么是单元测试和集成测试&#xff1f; 6. 软件的生命周期是什么样的&#xff1f; 需求…...

编程日记 2025/5/27 8:03:37

linux hungtask detect机制分析

1&#xff0c;机制概述‌ hungtask detect 是 Linux 内核用于检测长时间阻塞&#xff08;"hung"&#xff09;任务的机制&#xff0c;主要针对因死锁、死循环或资源竞争导致无法调度的任务 ‌触发条件‌&#xff1a;任务在 TASK_UNINTERRUPTIBLE 状态持续超过预设阈值…...

编程日记 2025/5/24 20:30:10

影刀处理 Excel：智能工具带来的高效变革

1. 高效的数据处理能力 1.1 快速读取与写入数据 影刀在处理 Excel 数据时展现出显著的读取与写入速度优势。传统方法处理大型 Excel 文件时&#xff0c;读取速度可能仅为每秒 100 行左右&#xff0c;而影刀通过优化底层代码和采用高效的文件解析算法&#xff0c;读取速度可达…...

编程日记 2025/5/29 15:18:20

2021ICPC四川省赛个人补题ABDHKLM

Dashboard - The 2021 Sichuan Provincial Collegiate Programming Contest - Codeforces 过题难度&#xff1a; A K D M H B L 铜奖 5 594 银奖 6 368 金奖 8 755 codeforces.com/gym/103117/problem/A 模拟出牌的过程&#xff0c;打表即可 // Code Start Here int t…...

编程日记 2025/5/24 0:58:35

HarmonyOS 影视应用APP开发--配套的后台服务go-imovie项目介绍及使用

网上有小伙伴对影视应用感兴趣&#xff0c;也想搞个自己的免费观影APP玩玩儿。前期博主开源的有uniapp版本和harmonyOS原生版本影视客户端&#xff0c;但是对博主开源的这个影视后台接口服务不太了解&#xff0c;不知道怎么用起来。这里总结介绍下该go-imove后台接口服务项目介…...

编程日记 2025/6/1 9:05:43

JAVA SE 多线程(上)

文章目录 &#x1f4d5;1. Thread类及常见方法✏️1.1 创建线程✏️1.2 Thread 的常见构造方法✏️1.3 Thread 的几个常见属性✏️1.4 启动一个线程---start()✏️1.5 中断一个线程---interrupt()✏️1.6 等待一个线程---join()✏️1.7 获取当前线程引用✏️1.8 休眠当前线程 &…...

编程日记 2025/5/28 0:31:41

基于Bootstrap 的网页html css 登录页制作成品

目录 前言 一、网页制作概述 二、登录页面 2.1 HTML内容 2.2 CSS样式 三、技术说明书 四、页面效果图 前言 ‌Bootstrap‌是一个用于快速开发Web应用程序和网站的前端框架&#xff0c;由Twitter的设计师Mark Otto和Jacob Thornton合作开发。 它基于HTML、CSS和JavaScri…...

编程日记 2025/5/31 15:02:56