当前位置：首页 > news >正文

【leetcode】逐层探索：BFS求解最短路的原理与实践

news 来源：原创 2025/6/12 20:54:37

前言

🌟🌟本期讲解关于力扣的几篇题解的详细介绍~~~

🌈感兴趣的小伙伴看一看小编主页：GGBondlctrl-CSDN博客

🔥 你的点赞就是小编不断更新的最大动力

🎆那么废话不多说直接开整吧~~

📚️1.BFS如何解决最短路问题

📚️2.迷宫中离入口最近的出口

🚀2.1题目描述

🚀2.2题目解析

🚀2.3题目代码

📚️3.最小基因变化

🚀3.1题目描述

🚀3.2题目分析

🚀3.3题目代码

📚️4.总结

📚️1.BFS如何解决最短路问题

在解决下面几道题之前，小编要展开讲讲为啥我们的BFS宽度优先遍历可以解决这里的最短路问题，我们在之前已经了解到，这个的宽度优先遍历BFS的遍历方法如同病毒扩散的方式进行扩散遍历，那么好就是一个关键

且看这张图：

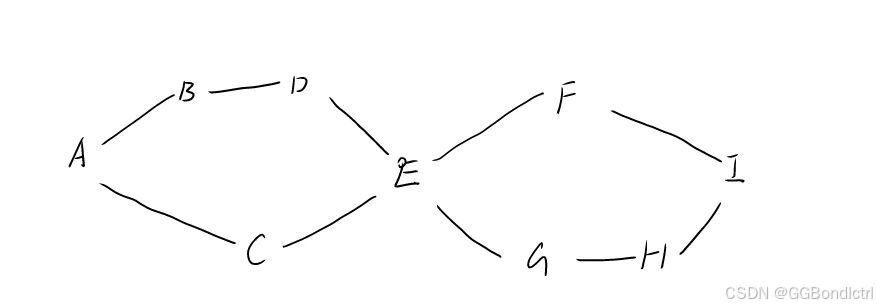
假如说，我们从A到我们的I，那么最短路径就是：

A C E F I

注意：BFS只适用于边权为一的情况；

那么BFS如何进行操作？

首先我们了解到BFS的扩散是一层一层的，那么我们就可以利用这个特性；

假如我们要找A到E的最短路径，那么如下图：

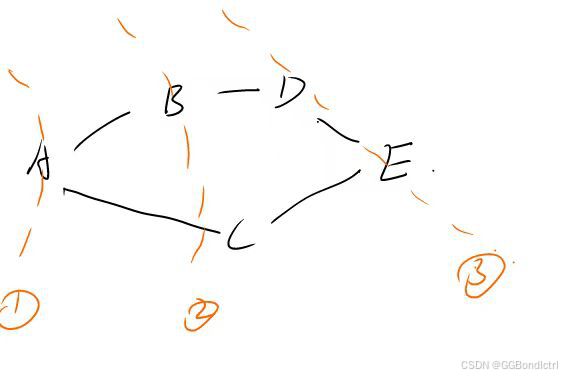
可以看到，我们与A连接的值就是BC两个节点，那么我们可以将BC看做一层，那么我们在以BC为一层，进行扩散，那么就会得到下一层就是DE，那么此时这一层就包含我们的目标节点，那么就可以知道我们到达E节点的步数了~~~

那么基于上述，我们重A到目标点I，的实例如下：

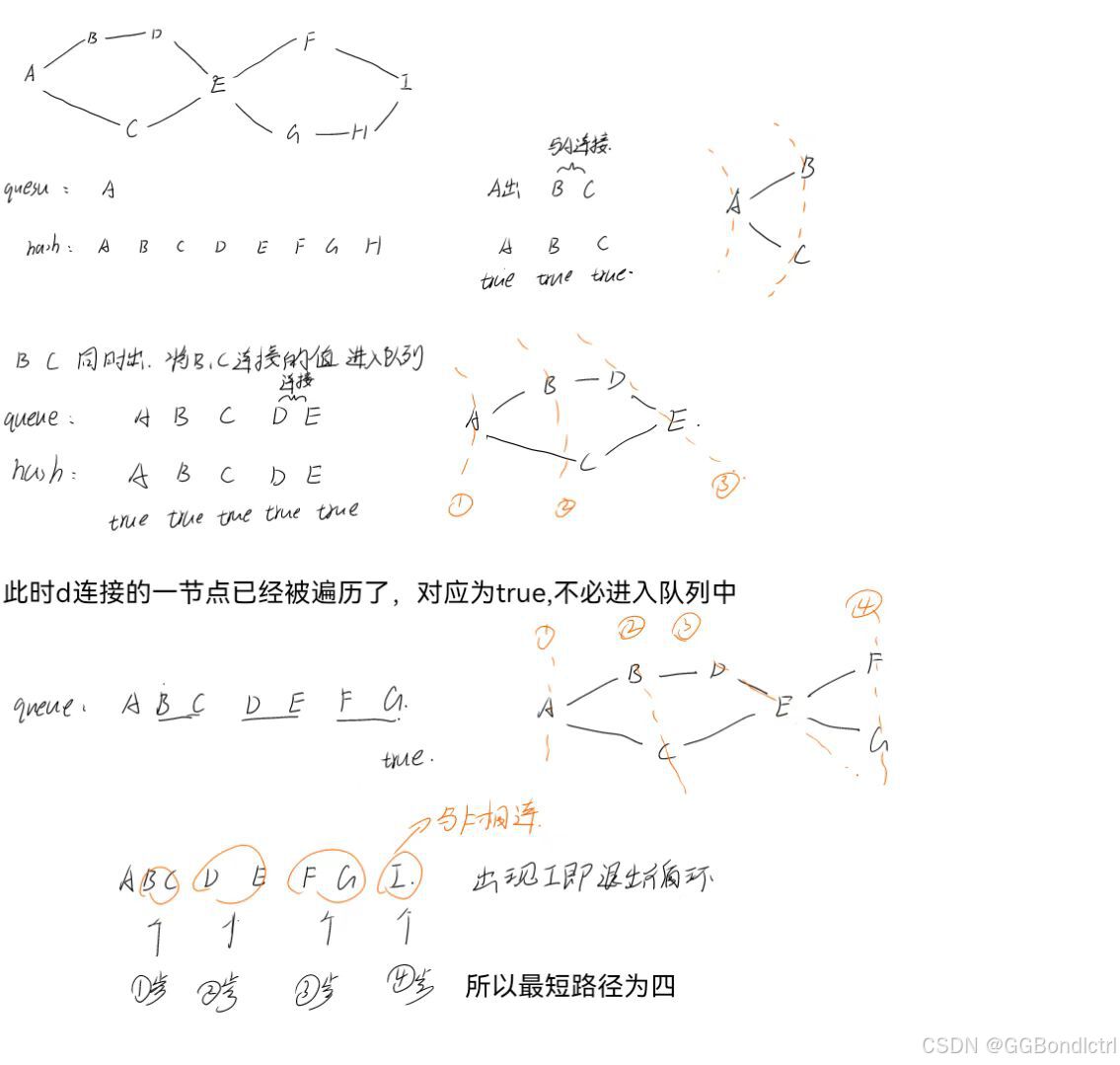
注意我们在遍历的过程中，已经被遍历的节点，那么对应就不能够进行遍历的操作了，那么在一层一层拨开后：

A层（BC层）（DE层）（FG层）

那么这就是我们的BFS解决最短路问题；

📚️2.迷宫中离入口最近的出口

🚀2.1题目描述

给你一个 m x n 的迷宫矩阵 maze （下标从 0 开始），矩阵中有空格子（用 '.' 表示）和墙（用 '+' 表示）。同时给你迷宫的入口 entrance ，用 entrance = [entrancerow, entrancecol] 表示你一开始所在格子的行和列。

每一步操作，你可以往上，下，左或者右移动一个格子。你不能进入墙所在的格子，你也不能离开迷宫。你的目标是找到离 entrance 最近的出口。出口的含义是 maze 边界上的 空格子。entrance 格子不算出口。

请你返回从 entrance 到最近出口的最短路径的步数，如果不存在这样的路径，请你返回 -1 。

如下：

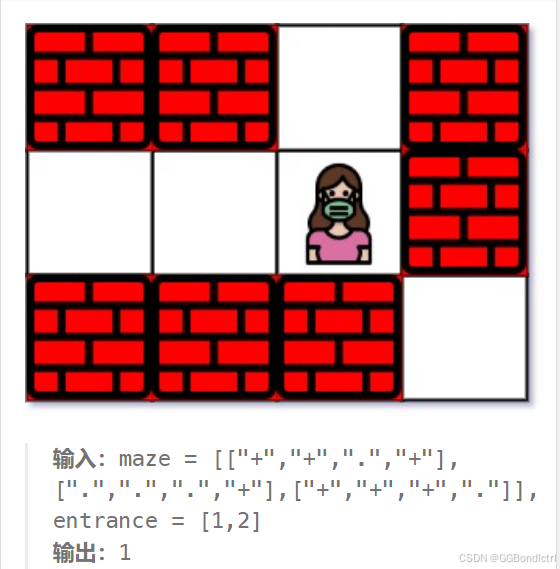
就是我们会出生在entrance的地方，然后找到最短的出口，返回我们离这个出口的距离

其中 “+”为墙，不可以触碰，不可以穿过；

🚀2.2题目解析

到这里就很明显了，我们使用BFS的最短路径解决办法，以入口为起点，开始扩散，如果扩散的一层到了边缘，那么就可以进行计算返回最短路径了；

解题思路：

1.创建队列，创建一个参照数组来规定哪些地址我们已经遍历了

2.将我们此时的位置放入队列中，然后此位置标记

3.在队列不可为空的时候，我们要拿出一层的节点来进行扩散操作，所以需要拿到此时队列的长度；

4.条件判断，入队列即可

🚀2.3题目代码

代码如下所示：

class Solution {int[] dx = { 0, 0, 1, -1 };int[] dy = { 1, -1, 0, 0 };public int nearestExit(char[][] maze, int[] entrance) {int m = maze.length;int n = maze[0].length;boolean[][] vis = new boolean[m][n];Queue<int[]> q = new LinkedList<>();q.add(new int[] { entrance[0], entrance[1] });vis[entrance[0]][entrance[1]] = true;int step = 0;while (!q.isEmpty()) {step++;int sz = q.size();for (int i = 0; i < sz; i++) {int[] index = q.poll();int a = index[0];int b = index[1];for (int k = 0; k < 4; k++) {int x = a + dx[k];int y = b + dy[k];if (x >= 0 && x < m && y >= 0 && y < n && vis[x][y] == false && maze[x][y] == '.') {if(x == 0 || x == m - 1 || y == 0 || y == n - 1){return step;}q.add(new int[] { x, y });vis[x][y] = true;}}}}return  -1;}
}

注意：我们在扩散的时候是上下左右四个方向的扩散，并且在BFS的时候，我们要将一层的节点拿出来进行扩散，再将这一层扩散的节点作为一下层来进行扩散，这就是为什么我们要计算队列的长度；

📚️3.最小基因变化

🚀3.1题目描述

基因序列可以表示为一条由 8 个字符组成的字符串，其中每个字符都是 'A'、'C'、'G' 和 'T' 之一。

假设我们需要调查从基因序列 start 变为 end 所发生的基因变化。一次基因变化就意味着这个基因序列中的一个字符发生了变化。

例如，"AACCGGTT" --> "AACCGGTA" 就是一次基因变化。

另有一个基因库 bank 记录了所有有效的基因变化，只有基因库中的基因才是有效的基因序列。（变化后的基因必须位于基因库 bank 中）

给你两个基因序列 start 和 end ，以及一个基因库 bank ，请你找出并返回能够使 start 变化为 end 所需的最少变化次数。如果无法完成此基因变化，返回 -1 。

注意：起始基因序列 start 默认是有效的，但是它并不一定会出现在基因库中。

总结：

就是将每个单词进行变化（可以变成A C G T）其中的一个，并且每次变化只要在基因库中存在，那么就是有效的变化，所以要求的就是从一个序列变成另一个序列的最短路径

🚀3.2题目分析

我就以题目的列子来进行举例吧：

如下图所示：

上述就是整个分析过程：

1.我们要对于一个序列上的每一个字符进行替换，在满足存在bank的情况下，将对应的序列进行入队列（作为一层），若不满足那么就不管；

2. 每一次进行替换的时候，都要将同一层的序列进行替换的操作，就是一步；所以这里要利用队列的长度

3.在添加序列进入队列中的时候，也要将对应序列进行记录表示已经出现过了，不能变化回去

4.在满足没有遍历过，并且存在bank中时，添加进入队列后，要判断是否是目标序列，返回我们的步数（一个变量，每次一层搞完后，就加一即可）

🚀3.3题目代码

代码如下所示：

class Solution {public int minMutation(String startGene, String endGene, String[] bank) {//首先将我们的基因库存入哈希表中Set<String> isBank = new HashSet<>();for (String s : bank) {//判断存在即可isBank.add(s);}if(startGene.equals(endGene)){return 0;}if(!isBank.contains(endGene)){return -1;}Queue<String> q = new LinkedList<>();int step = 0;//定义一个哈希表来判断是否已经遍历过了Map<String, Boolean> vis = new HashMap<>();//两层循环q.add(startGene);vis.put(startGene, true);while (!q.isEmpty()) {step++;int count = q.size();for (int k = 0; k < count; k++) {String str = q.poll();for (int i = 0; i < str.length(); i++) {//进行四次变化for (int j = 0; j < 4; j++) {char ch = 'R';if(j == 0){ch = 'A';}else if(j == 1){ch = 'C';}else if(j == 2){ch = 'G';}else if(j == 3){ch = 'T';}StringBuilder sb = new StringBuilder(str);sb.setCharAt(i, ch);String sb_str = sb.toString();if(isBank.contains(sb_str) && !vis.containsKey(sb_str)){if(sb_str.equals(endGene)){return step;}q.add(sb_str);vis.put(sb_str,true);}}}}}return -1;}
}

其实大体的思路和上面的迷宫题目差不多，就是一层一层进行剥去，这里的核心剥去就是一队列长度为循环条件，直到一层出完，并扩散至另一层后才会开启下一层的扩散~~~

📚️4.总结

本期小编主要讲解了关于BFS如何解决最短路径的问题，其主要思想就是利用BFS进行层层扩散，并一层一层剥离的思想，来决定最短路径

1926. 迷宫中离入口最近的出口 - 力扣（LeetCode）

433. 最小基因变化 - 力扣（LeetCode）

🌅🌅🌅~~~~最后希望与诸君共勉，共同进步！！！

💪💪💪以上就是本期内容了，感兴趣的话，就关注小编吧。

😊😊 期待你的关注~~~

📚️1.BFS如何解决最短路问题

📚️2.迷宫中离入口最近的出口

🚀2.1题目描述

🚀2.2题目解析

🚀2.3题目代码

📚️3.最小基因变化

🚀3.1题目描述

🚀3.2题目分析

🚀3.3题目代码

📚️4.总结

相关文章：