当前位置：首页 > news >正文

Graph Representation Learning【图最短路径优化/Node2vec/Deepwalk】

news 来源：原创 2025/6/21 14:58:45

文章目录

- - Q1：
  - - 网络性质：
    - - 1.数据读取与邻接表构建：
      - 2.基本特征和连通性：
    - 算法思路：
    - - 1. 广度优先搜索（BFS）标记前驱:
      - 2. 回溯生成所有最短路径:
    - 实验结果：
    - 复杂度分析：
  - Q2：
  - - 算法思路：
    - - 初始化
    - 实验结果：
    - 复杂度分析：
  - Q3：
  - - 图表示学习：
    - 实验结果：
    - - 结果分析：
      - ps：为什么不同距离度量的样本区分度大有不同？
    - 别的尝试：
  - 参考：

Q1：

DDI网络构建无向图并找出指定节点i和j的所有最短距离

DDI网络可表示为：
$G_{small}=(V_{small},E_{small})\\ V_{small}=\{1,2,3,4\} \\E_{small}=\{(1,2),(1,3),(1,4),(3,4)\}$

网络性质：

无向无权的大规模稀疏图，我们一般用邻接表存储：

1.数据读取与邻接表构建：

遍历所有边，为每个节点维护其邻接节点列表。对于边 ( (u, v) )，将 ( v ) 加入 ( u ) 的邻接列表，并将 ( u ) 加入 ( v ) 的邻接列表。
$\text{Adj}[u] \leftarrow \text{Adj}[u] \cup \{v\}, \quad \text{Adj}[v] \leftarrow \text{Adj}[v] \cup \{u\}$

2.基本特征和连通性：

通过dfs得到图的连通性结果如下

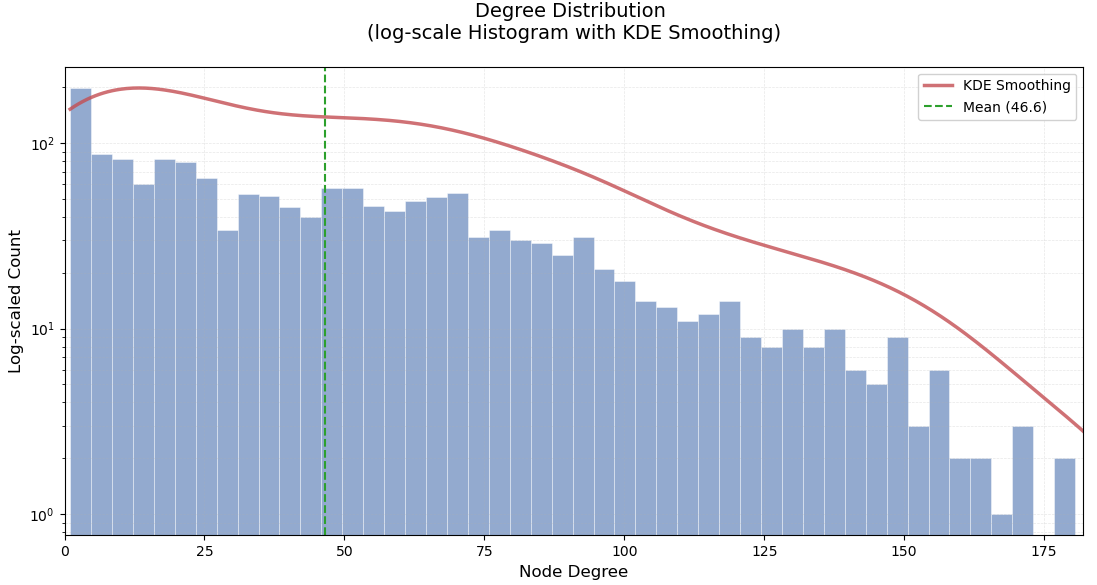
在这里插入图片描述

每个节点平均连接到大约47个其他节点
这意味着整个图是一个单一的连通组件，没有孤立的子图，整个网络是完全连通的，任何两个节点之间都存在路径相连

以下为度数分布图：

在这里插入图片描述

算法思路：

寻找两点之间的所有最短路径，使用**BFS+回溯**, 因为由上面的分析可知，图的平均度数很高，较为密集，最短路径长度较短，所以递归深度不会太高。
但是在路径回溯阶段，虽然直观易实现，但在最短路径数量较多的情况下，递归深度和调用栈开销可能迅速增长，性能下降甚至栈溢出。所以先使用显式栈进行迭代回溯。
在回溯过程中，某些节点的路径可能会被多次访问。记忆化缓存可以保存已经计算过的路径，避免再次计算。

1. 广度优先搜索（BFS）标记前驱:

初始化距离 (d[s] = 0)，其余节点 ( d[v] = inf )。
使用队列逐层扩展，更新节点的最短距离和前驱节点：
$\forall v \in \text{Adj}[u], \quad \text{若 } d[v] > d[u] + 1 \implies d[v] \leftarrow d[u] + 1, \ \text{prev}[v] \leftarrow \{u\} \\ \text{若 } d[v] = d[u] + 1 \implies \text{prev}[v] \leftarrow \text{prev}[v] \cup \{u\}$
当队列为空时结束。

2. 回溯生成所有最短路径:

从终点 ( t ) 启动，使用显式栈模拟递归过程，逐步构建所有从起点 ( s ) 到终点 ( t ) 的最短路径。与传统的回溯方法不同，这里我们利用记忆化搜索来缓存计算过的路径，以减少不必要的重复计算。

使用栈中元素表示当前遍历状态：(当前节点, 当前路径)。
如果当前节点是起点 s，则路径已经完整，逆序将路径加入结果集中。
如果当前节点不是起点，首先检查该节点是否已经有缓存路径（通过 memo 字典）。如果有，则直接从缓存中取出路径；否则，遍历当前节点的前驱节点，将所有可能的路径推入栈中。

实验结果：

对于（8,309）、（67,850）、（990,1256）药物的最短路径：
在这里插入图片描述

使用time模块：对于最短路径较多的用时较少。

在这里插入图片描述

复杂度分析：

BFS会遍历所有边和节点来计算最短路径，并且回溯最短路径时涉及到路径构建
实际最坏时间复杂度比没有缓存时更低，但是由于使用了记忆化搜索，减少了重复计算

$\cdot L)~~~~~\\V为节点数，E为边数，K是路径数量,L是路径最大长度$

Q2：

计算所有正负药物对的最短距离并可视化对比两类样本的结果

列表	数据含义	药物对的数量
DDIpos	DDI网络中存在相互作用的药物对（正样本）	1601
DDIneg	DDI网络中没有相互作用的药物对（负样本）	1601