【数据结构】手撕AVL树(万字详解)

AVL树的概念

为啥要有AVL树？

在上一章节的二叉搜索树中，我们在插入节点的操作中。有可能一直往一边插入节点，这就导致我们的二叉搜索树退化出一颗单支树，那么他的查找效率就和链表是一样的了。

概念

• 因此对于上面的问题，两位俄罗斯的数学家G.M.A delson-Velskii和E.M.Landis在1962年发明了解决上述问题的方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1（需要对树中的结点进行调整），即可降低树的高度，从而减少平均搜索长度。

• AVL树可以是一棵空树，也可以是具有以下性质的一棵二叉搜索树：

  1. 树的左右子树都是AVL树。
  2. 树的左右子树高度之差（简称平衡因子）的绝对值不超过1（-1/01）。

• 如果一颗二叉搜索树的高度是平衡的，那么他就是AVL树，AVL树保持了两边高度的平衡，那么查找效率就是o(logN)

• 注意的是我们AVL树是不能让两边高度之差是0的，只有满二叉树才能保证。

AVL树节点的定义

我们这里直接实现KV模型的AVL树，为了方便后续的操作，这里将AVL树中的结点定义为三叉链结构(也就是多了一个parent，为什么后面讲解)，并在每个结点当中引入平衡因子（右子树高度-左子树高度）。除此之外，还需编写一个构造新结点的构造函数，由于新构造结点的左右子树均为空树，于是将新构造结点的平衡因子初始设置为0即可。

template<class K, class V>
struct AVLTreeNode
{//三叉链AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;//存储的键值对pair<K, V> _kv;//平衡因子(balance factor)int _bf; //右子树高度-左子树高度//构造函数AVLTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0){}
};

AVL树的插入

• AVL树的插入有以下三个步骤
  1. 按照二叉搜索树的插入方式，先搜索插入位置
  2. 找到插入位置后，把节点插入到该为位置中。
  3. 从现在位置开始向上更新平衡因子，如果出现不平衡，需要旋转。

因为AVL树本身就是一棵二叉搜索树，因此寻找结点的插入位置是非常简单的，按照二叉搜索树的插入规则：

1. 待插入结点的key值比当前结点小就插入到该结点的左子树。
2. 待插入结点的key值比当前结点大就插入到该结点的右子树。
3. 待插入结点的key值与当前结点的key值相等就插入失败。

与二叉搜索树的不同点是，AVL树每次插入一个新节点就需要向上更新平衡因子，因为插入的节点会影响上面子树的平衡因子

由于一个结点的平衡因子是否需要更新，是取决于该结点的左右子树的高度是否发生了变化，因此插入一个结点后，该结点的祖先结点的平衡因子可能需要更新。

• 所以我们插入结点后需要倒着往上更新平衡因子，更新规则如下：
  1. 新增结点在parent的右边，parent的平衡因子++.
  2. 新增结点在parent的右边，parent的平衡因子+ +
• 这也是我们为啥要使用parent来实现三叉链的原因，因为我们需要向上更新平衡因子，判断这个子树是否需要旋转来保持左右高度平衡。

每更新完一个结点的平衡因子后，都需要进行以下判断：

• 如果parent的平衡因子等于-1或者1，表明还需要继续往上更新平衡因子。
• 如果parent的平衡因子等于0，表明无需继续往上更新平衡因子了。
• 如果parent的平衡因子等于-2或者2，表明此时以parent结点为根结点的子树已经不平衡了，需要进行旋转处理。

判断理由的说明：

• 1/-1,只有从0经过–/++的操作才能变成-1/1, 比如以parent为根节点的子树，开始并没有左右孩子，往左边插入新节点就是-1,往右边插入新节点就是1，这样的插入操作导致parent为根节点的子树高度发生了变化，这个时候parent也可能是别人的孩子节点，所以需要向上更新平衡因子，检查他的父节点的平衡因子做出对应的操作
  
  
• 平衡因子为0，这种情况以parent为根节点的子树一定是一边的高度高和一边的高度矮，并且插入的新节点一定是插入到矮的那边，导致左右高度相等，那么根节点的左右子树高度相等，平衡因子是左右高度子树之差，那么相互抵消，就是0

• 平衡因子是-2或2，此时parent结点的左右子树高度之差的绝对值已经超过1了，不满足AVL树的要求，因此需要进行旋转处理。
  

若是在更新平衡因子的过程当中，出现了平衡因子为-2/2的结点，这时我们需要对以该结点为根结点的树进行旋转处理，而旋转处理分为四种，在进行分类之前我们首先需要进行以下分析：

• 我们将插入的新节点称为cur, 他的父节点称为parent，我们插入成功后，第一个更新的平衡因子的节点就是parent这个节点的平衡因子，现在如果我们的parent平衡因子是-1/1需要继续往上更新parent的parent的平衡因子，那么如果想要往上更新找到parent的parent节点就需要执行下面的语句

cur = parent;
parent = parent->_parent;

• 这里我想说明一点，如果parent的平衡因子是-2/2，那么cur(他的孩子节点)一定是-1/1而不会是0.
• 证明一下：假设cur的平衡因子是0，那么他一定是一个新增节点，因为只有新增节点才能会往上更新parent的平衡因子。反之，如果这里不是新增节点而是之前向上更新的节点把他平衡因子更新为0，那么在cur哪里就已经结束了，我们说过平衡因子为0就代表以当前节点为根节点的子树已经平衡直接break， 所以当前节点的父节点不可能是-2/2，因为当前节点就break了，不会更新到-2/2
• 而如果当前节点是一个新增节点的话，他的父节点的平衡因子只能是-1/0/1其中的一种。在新增结点插入前，其父结点的状态有以下两种可能：
  1. 其父结点是一个左右子树均为空的叶子结点，其平衡因子是0，新增结点插入后其平衡因子更新为-1/1。
  2. 其父结点是一个左子树或右子树为空的结点，其平衡因子是-1/1，新增结点插入到其父结点的空子树当中，使得其父结点左右子树当中较矮的一棵子树增高了，新增结点后其平衡因子更新为0。
• 综上所述，当parent的平衡因子为-2/2时，cur的平衡因子必定是-1/1而不会是0。

根据此结论，我们可以将旋转处理分为以下四类：

• 当parent的平衡因子是-2的，cur的平衡因子是-1的时候，需要右单旋。
  
• 当parent的平衡因子是2，cur的平衡因子是1的时候，需要左单旋
  
• 当parent的平衡因子是-2，cur的平衡因子是1的时候，需要左右单旋
  
• 当parent对的平衡因子是2, cur的平衡因子是01的时候，需要右左单旋

• 并且，在进行旋转处理后就无需继续往上更新平衡因子了，因为旋转后树的高度变为插入之前了，即树的高度没有发生变化，也就不会影响其父结点的平衡因子了。具体原因请看后面的旋转讲解。

AVL树的旋转

左单旋

• 旋转示意图
  
• 左单旋的步骤如下
  1. 让subR的左子树作为parent的右子树
  2. 让parent作为subR的左子树。
  3. 让subR作为整个子树的根。
  4. 更新平衡因子。
• 左单旋后满足二叉搜索树的性质
  1. subRL本身就比parent大，因此可以作为parent的右子树
  2. parent及其左子树本身就比subR的值小，因此可以作为subR的左子树。
• 平衡因子的更新如下:
  
• 可以看到，经过左单旋后，树的高度变为插入之前了，即树的高度没有发生变化，所以左单旋后无需继续往上更新平衡因子。
• 这里我再说一个问题。我们的subRL子树有没有情况是为空的？
  
• 代码如下

//左单旋
void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;Node* parentParent = parent->_parent;//1、建立subR和parent之间的关系parent->_parent = subR;subR->_left = parent;//2、建立parent和subRL之间的关系parent->_right = subRL;if (subRL)subRL->_parent = parent;//3、建立parentParent和subR之间的关系if (parentParent == nullptr)	//如果说parent是祖宗节点，那么他的父节点一定是空的，subR更新为祖宗节点{_root = subR;subR->_parent = nullptr; //subR的_parent指向需改变}else	//如果说不是祖宗节点，那么parent一定是某棵子树的跟节点判断parent是他的父节点的左孩子还是右孩子，并更新subR。{if (parent == parentParent->_left){parentParent->_left = subR;}else //parent == parentParent->_right{parentParent->_right = subR;}subR->_parent = parentParent;}//4、更新平衡因子subR->_bf = parent->_bf = 0;
}

右单旋

• 右单旋的步骤如下：

  1. 让subL的右子树作为parent的左子树
  2. 让parent作为subL的右子树
  3. 让subL作为整个子树的根
  4. 更新平衡因子

• 右单旋后满足二叉搜索树的性质

  1. subL的右子树本身就比parent这颗子树要小，因此可以作为parent的左子树。
  2. parent及其右子树当中结点的值本身就比subL的值大，因此可以作为subL的右子树。

• 平衡因子的更新如下
  

• 可以看到，经过右单旋后，树的高度变为插入之前了，即树的高度没有发生变化，所以右单旋后无需继续往上更新平衡因子。

//右单旋
void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;Node* parentParent = parent->_parent;//1、建立subL和parent之间的关系subL->_right = parent;parent->_parent = subL;//2、建立parent和subLR之间的关系parent->_left = subLR;if (subLR)subLR->_parent = parent;//3、建立parentParent和subL之间的关系if (parentParent == nullptr){_root = subL;_root->_parent = nullptr;}else{if (parent == parentParent->_left){parentParent->_left = subL;}else //parent == parentParent->_right{parentParent->_right = subL;}subL->_parent = parentParent;}//4、更新平衡因子subL->_bf = parent->_bf = 0;
}

左右双旋

• 左右双旋，顾名思义就是先左单旋，然后右单旋，最后需要右单旋就是因为他是左子树的高度太高了。那为啥在右单旋之前需要左单旋呢？就是因为我们左子树的高度并不是单纯的左子树高，他的子树中是右子树高了，所以需要右单旋。(综合图来看)

• 左右双旋后满足二叉搜索树的性质
  1. subLR中的左子树本身就比subL要大，所以可以作为subL的右子树。
  2. subLR中的右子树本身就比parent要小，所以可以作为parent的左子树
  3. 经过步骤1/2后，subL中的值都比subLR的要小，parent中的值都比subLR要大，所以subL和parent分别可以作为subLR的左右子树。’

• 具体的旋转示意图如下：
  
  

• 左右双旋后，平衡因子的更新随着subLR原始平衡因子的不同分为以下三种情况：

1、当subLR原始平衡因子是-1时(其实就是新增节点插入到右子树高的那个子树的左子树中)，左右双旋后parent、subL、subLR的平衡因子分别更新为1、0、0。

2、当subLR原始平衡因子是1时(其实就是新增节点插入到右子树高的那个子树(subLR)的右子树中)，左右双旋后parent、subL、subLR的平衡因子分别更新为0、-1、0。

3、当subLR原始平衡因子是0时,左右双旋后parent、subL、subLR的平衡因子分别更新为0、0、0。

• 可以看到，经过左右双旋后，树的高度变为插入之前了，即树的高度没有发生变化，所以左右双旋后无需继续往上更新平衡因子。
• 左右双旋的步骤如下
  1. 以subL为轴左旋，之所以需要左旋以subL为根节点的子树就是因为以parent为根节点的子树的左边高度是subL这颗子树来支撑，但是subL的高度却是主要是右边高，所以需要左旋subL把subL为根的这颗子树变成单纯的左边高，parent这颗子树才能单纯的左边高。
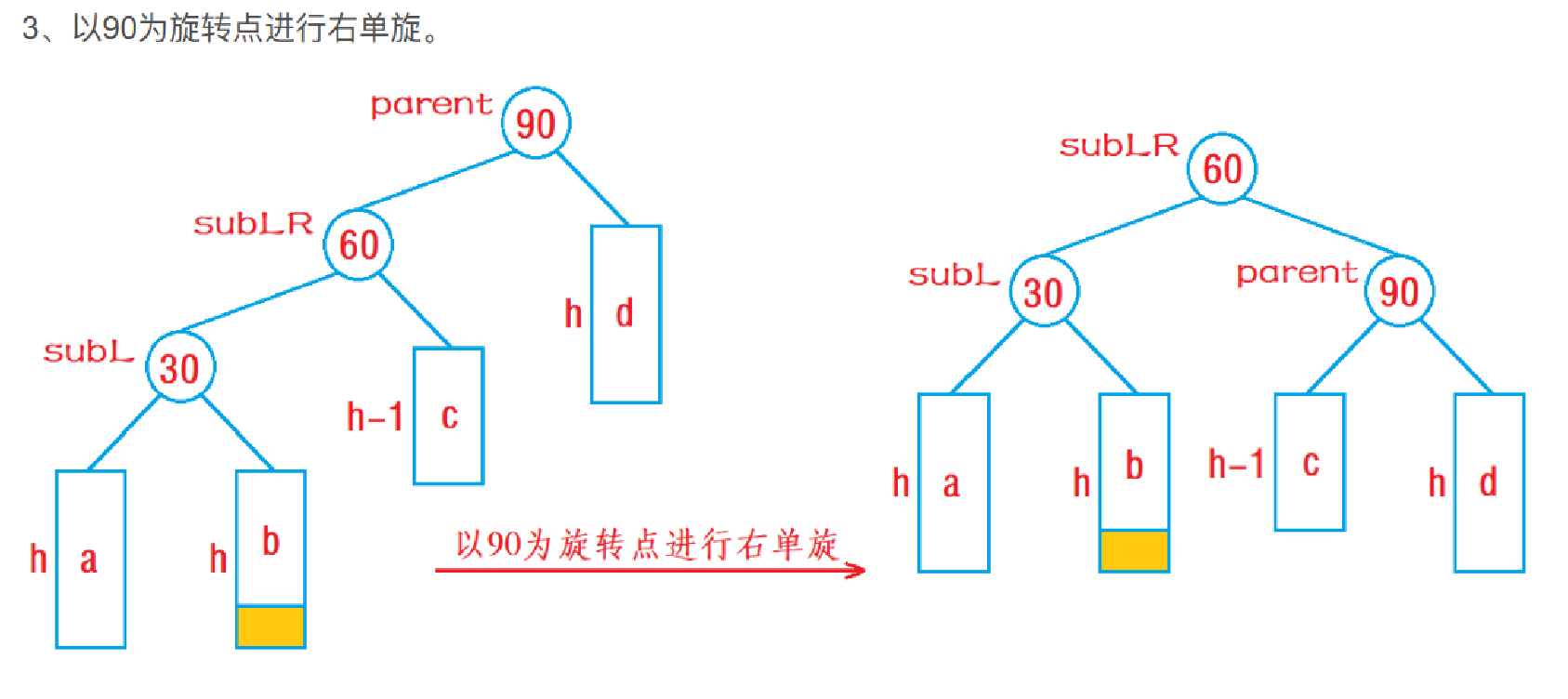
  2. 以parent为旋转点进行右单旋。(这个时候parent为根节点的子树已经变成单纯的左边高)
  3. 更新平衡因子。

代码如下：

//左右双旋
void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf; //subLR不可能为nullptr，因为subL的平衡因子是1//1、以subL为旋转点进行左单旋RotateL(subL);//2、以parent为旋转点进行右单旋RotateR(parent);//3、更新平衡因子if (bf == 1){subLR->_bf = 0;subL->_bf = -1;parent->_bf = 0;}else if (bf == -1){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 1;}else if (bf == 0){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 0;}else{assert(false); //在旋转前树的平衡因子就有问题}
}

右左双旋

• 具体看图
  

• 我们再举一个具体的例子来说

• 右左双旋的步骤如下
  1. 以subR为旋转点进行右单旋（把parent为根的子树变成单纯的右边高）
  2. 以parent为旋转点进行左单旋 (这个时候就是单纯的右边高了，可以进行左单旋)
  3. 更新平衡因子
• 右左双旋后满足二叉搜索树的性质：
  右左双旋后，实际上就是让subRL的左子树和右子树，分别作为parent和subR的右子树和左子树，再让parent和subR分别作为subRL的左右子树，最后让subRL作为整个子树的根（结合图理解）。

1. subRL的左子树本来就比parent的值要大，可以作为parent的右子树
2. subRL的右子树本来就比subR的值要小，因此可以作为subR的左子树
3. 经过步骤1/2后, parent子树比subRL的值要小， subRL要比subR的值要小，所以subRL可以作为整颗树的根节点，parent和subR作为他的左子树和右子树。

右左双旋后，平衡因子的更新随着subLR原始平衡因子的不同分为以下三种情况：

• 1、当subRL原始平衡因子是1时，左右双旋后parent、subR、subRL的平衡因子分别更新为-1、0、0。
  
• 2、当subRL原始平衡因子是-1时，左右双旋后parent、subR、subRL的平衡因子分别更新为0、1、0。
  
• 3、当subRL原始平衡因子是0时，左右双旋后parent、subR、subRL的平衡因子分别更新为0、0、0。
  
• 可以看到，经过右左双旋后，树的高度变为插入之前了，即树的高度没有发生变化，所以右左双旋后无需继续往上更新平衡因子。

//右左双旋
void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;//1、以subR为轴进行右单旋RotateR(subR);//2、以parent为轴进行左单旋RotateL(parent);//3、更新平衡因子if (bf == 1){subRL->_bf = 0;parent->_bf = -1;subR->_bf = 0;}else if (bf == -1){subRL->_bf = 0;parent->_bf = 0;subR->_bf = 1;}else if (bf == 0){subRL->_bf = 0;parent->_bf = 0;subR->_bf = 0;}else{assert(false); //在旋转前树的平衡因子就有问题}
}

AVL树的查找

• AVL树的查找函数与二叉搜索树的查找方式一模一样，逻辑如下：

1. 若树为空树，则查找失败，返回nullptr。
2. 若key值小于当前结点的值，则应该在该结点的左子树当中进行查找。
3. 若key值大于当前结点的值，则应该在该结点的右子树当中进行查找。
4. 若key值等于当前结点的值，则查找成功，返回对应结点。

代码如下：

//查找函数
Node* Find(const K& key)
{Node* cur = _root;while (cur){if (key < cur->_kv.first) //key值小于该结点的值{cur = cur->_left; //在该结点的左子树当中查找}else if (key > cur->_kv.first) //key值大于该结点的值{cur = cur->_right; //在该结点的右子树当中查找}else //找到了目标结点{return cur; //返回该结点}}return nullptr; //查找失败
}

AVL树的验证

AVL树是在二叉搜索树的基础上加了平衡的性质，如果说我们要验证一棵树是否是AVL树。首先我们需要验证他是否是一颗二叉搜索树。

• 二叉搜索树的一个特性是中序遍历下来是升序的，所以我们可以写一个中序遍历来验证是否是二叉搜索树

//中序遍历
void Inorder()
{_Inorder(_root);
}
//中序遍历子函数
void _Inorder(Node* root)
{if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.first << " ";_Inorder(root->_right);
}

• 但中序有序只能证明是二叉搜索树，要证明二叉树是AVL树还需验证二叉树的平衡性，在该过程中我们可以顺便检查每个结点当中平衡因子是否正确
• 采用后序遍历，变量步骤如下：
  1. 从叶子结点处开始计算每课子树的高度。（每棵子树的高度 = 左右子树中高度的较大值 + 1）
  2. 先判断左子树是否是AVL树。
  3. 再判断右子树是否是AVL树
  4. 如果左右子树都是AVL树，那么把左右子树的高度返回上一层，继续判断上一层的子树是否是平衡二叉树，直到判断到根为止。（若判断过程中，某一棵子树不是平衡二叉树，则该树也就不是平衡二叉树了）
     

	int Height(){return _Height(_root);}int _Height(Node* root){if (root == nullptr){return 0;}int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}bool IsBalanceTree(){return _IsBalanceTree(_root);}bool _IsBalanceTree(Node* root){// 空树也是AVL树if (nullptr == root)return true;// 计算pRoot结点的平衡因子: 即pRoot左右子树的高度差int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);int diff = rightHeight - leftHeight;// 如果计算出的平衡因子与pRoot的平衡因子不相等，或者// pRoot平衡因子的绝对值超过1，则一定不是AVL树	``if (abs(diff) >= 2){cout << root->kv.first << "高度差异常" << endl;return false;}if (root->_bf != diff){cout << root->kv.first << "平衡因子异常" << endl;return false;}// pRoot的左和右如果都是AVL树，则该树一定是AVL树return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);}

end

希望对大家有帮助，如果方便的话给博主点个赞哦，会让博主更有动力的。