当前位置： 首页 > news >正文

【递归、搜索和回溯】递归、搜索和回溯介绍及递归类算法例题

news 来源：原创 2025/8/5 14:51:07

个人主页 ： zxctscl
专栏 【C++】、 【C语言】、 【Linux】、 【数据结构】、 【算法】
如有转载请先通知

文章目录

  • 递归、搜索和回溯
    • 递归
    • 搜索VS 深度优先遍历 VS 深度优先搜索 VS 宽度优先遍历 VS 宽度优先搜索 VS 暴搜
    • 回溯与剪枝
  • 1 面试题 08.06. 汉诺塔问题
    • 1.1 分析
    • 1.2 代码
  • 2 21. 合并两个有序链表
    • 2.1 分析
    • 2.2 代码
    • 2.3 总结
  • 3 206. 反转链表
    • 3.1 分析
    • 3.2 代码
  • 4 24. 两两交换链表中的节点
    • 4.1 分析
    • 4.2 代码
  • 5 50. Pow(x, n)
    • 5.1 分析
    • 5.2 代码

递归、搜索和回溯

搜索是递归的一个分支，回溯是搜索里面的分支。

递归

  1. 什么是递归？
    在数据结构二叉树、快排和归并都有提到
    递归就是函数自己调用自己的情况

  2. 为什么会用到递归
    二叉树的后序遍历：左子树、右子树、根
    在快排中，先选择一个基准元素将数组分成两部分，左边排一下序，右边排一下序
    在归并排序中，选择一个中间点，把数组平分，先让左边排一下序，再让右边排一下序，再把两个有序数组合并
    在这里插入图片描述
    递归的本质：
    主问题->相同的子问题
    子问题->相同的子问题

  3. 如何理解递归
    （1）递归展开的细节图
    （2）二叉树的题目
    （3）宏观看待递归过程：
    一、不要在意递归细节展开图
    二、把递归的函数当成一个黑盒（具体里面如何操作的并不关心，只要能输出结果）
    三、相信这个黑盒一定能完成这个任务
    在这里插入图片描述

  4. 如何写好递归
    （1）先找到相同的子问题->函数头的设计
    （2）只关心某一个子问题是如何解决的->函数体的书写
    （3）注意一下递归函数的出口即可

搜索VS 深度优先遍历 VS 深度优先搜索 VS 宽度优先遍历 VS 宽度优先搜索 VS 暴搜

  1. 深度优先遍历 VS 深度优先搜索->dfs
    宽度优先遍历 VS 宽度优先搜索->bfs
    一定程度上等同
    遍历是形式，目的是搜索
    在这里插入图片描述

  2. 关系图
    暴力枚举一遍所有的结果
    搜索（也叫暴搜）分为两种：dfs、 bfs
    递归主要是dfs

  3. 拓展搜索问题
    全排列 树状图
    在这里插入图片描述

回溯与剪枝

  1. 回溯
    回溯本质就是深搜

1 面试题 08.06. 汉诺塔问题

在这里插入图片描述

1.1 分析

  1. 题目解析
    中间摆放的时候必须是小盘子在大盘子的上面

  2. 算法原理
    （1）如何解决汉洛塔问题？
    当N=1，直接把A上面的盘子放到C上。
    当N=2，想要把最大的盘子放到C上，此时先得把上面的小盘子放到B上，当把A剩下的大盘子直接移动到C上后，再将B上的小盘子放到C上。
    当N=3时候，首先把A最下面盘子移动到C，前提就得将A上面的2个盘子放到B上（就像N=2时，把上面两个盘子借助C移到B上）再将A最下面的盘子放到C上，最后把B上的盘子移到C上。
    当N=4时，首先把A最下面盘子移动到C，前提就得将A上面的3个盘子（当做一个整体）放到B上（就像N=3时，把上面两个盘子借助C移到B上）再将A最下面的盘子放到C上，最后把B上的盘子移到C上。
    …
    当N=n，也同样是首先把A最下面盘子移动到C，前提就得将A上面的n-1个盘子（当做一个整体）放到B上（就像N=n-1时，把上面两个盘子借助C移到B上）再将A最下面的盘子放到C上，最后把B上的盘子移到C上。

在这里插入图片描述
（2）为什么用递归？
大问题->相同问题的子问题
子问题->相同问题的子问题

（3）如何编写递归代码？
一、重复子问题->函数头
先把X柱子上的盘子，借助Y柱子，转移到Z柱子上
需要三个柱子，还有盘子的数量，就需要传四个参数

void dfs(X,Y,Z,int n)

二、只关心某一个子问题在做什么->函数体
（1）将X上面n-1盘子，借助Z，转移到Y上dfs(X,Z,Y,n-1)
（2）把A最下面盘子移到Z上
（3）再将Y上n-1个盘子借助X移到Z上dfs(Y,X,Z,n-1)
在这里插入图片描述

三、递归出口
当N=1时，把X上盘子放到Z上
在这里插入图片描述

  1. 编写代码

  2. 递归的细节展开图
    在这里插入图片描述

1.2 代码

class Solution {
public:void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {      dfs(A,B,C,A.size());     }void dfs(vector<int>& A, vector<int>& B, vector<int>& C,int n){if(n==1){C.push_back(A.back());A.pop_back();return;}dfs(A,C,B,n-1);C.push_back(A.back());A.pop_back();dfs(B,A,C,n-1);}
};

2 21. 合并两个有序链表

在这里插入图片描述

2.1 分析

算法原理
解法：递归

两个链表都是升序，找两个链表头结点中较小的节点作为返回的头节点。
当选择头节点之后，就是将剩下的两个链表合并
在这里插入图片描述

（1）重复子问题->函数头
合并两个有序链表 Node*dfs(l1,l2)

（2）只关心某一个子问题在做什么事情->函数体的设计
一、比大小
二、如果l1较小 ：l1->next=dfs(l1->next,l2)
三、return l1

（3）递归出口

谁为空返回另一个

在这里插入图片描述

2.2 代码

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2){if(list1==nullptr)return list2;if(list2==nullptr)return list1;if(list1->val<=list2->val){list1->next=mergeTwoLists(list1->next,list2);return list1;}else{list2->next=mergeTwoLists(list1,list2->next);return list2;}}};

2.3 总结

  1. 递归VS循环 什么时候用循环舒服？什么时候用递归舒服？
    递归和循环都是重复子问题，递归和循环之间可以相互转换

递归图越复杂，递归就越舒服

  1. 递归VS深搜
    递归展开图，其实就是对一棵树做一次深度优先搜索遍历（dfs）
    在这里插入图片描述

3 206. 反转链表

在这里插入图片描述

3.1 分析

解法：递归

第一个视角：从宏观角度

  1. 把当前节点后面链表先逆置，并且把头结点返回；
  2. 把当前节点添加到逆置链表的后面
  3. 当遇到null就返回
    在这里插入图片描述

第二个视角：将链表看成一棵树
先找到叶子结点，再返回
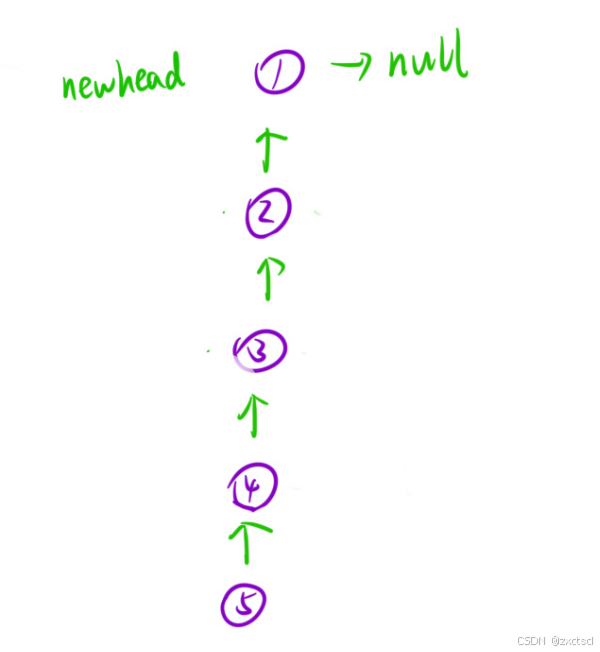
在这里插入图片描述

在这里插入图片描述

3.2 代码

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* reverseList(ListNode* head) {if(head==nullptr||head->next==nullptr)return head;ListNode* newhead=reverseList(head->next);head->next->next=head;head->next=nullptr;return newhead;}
};

4 24. 两两交换链表中的节点

在这里插入图片描述

4.1 分析

解法：递归
视角：从宏观角度看待递归

想要两两逆置，把后面的那堆先两两逆置一下，后面的调用完dfs后，再返回后面部分的头结点，再把前面两个交换一下，把交换后的连起来。
在这里插入图片描述

在这里插入图片描述

4.2 代码

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* swapPairs(ListNode* head) {if (head == nullptr || head->next == nullptr)return head;ListNode* tmp = swapPairs(head->next->next);ListNode* ret = head->next;head->next->next = head;head->next = tmp;return ret;}
};

5 50. Pow(x, n)

在这里插入图片描述

5.1 分析

解法：一、暴力循环
对于太大的幂是会超时的

二、快速幂
实现快速幂：（1）递归（2）循环

这里用递归

如果快速得到3的16次方，得到3的8次方就行，要3的8次方得到3的4次方就行，要得到3的4次方，得到3的2次方就行，要得到3，就直接3乘1就行。这里时间复杂度就是logN

那么如果除不进时，21/2除不进，就能可以分为3的10次方乘3的10次方再乘3就行，一直这样
在这里插入图片描述

（1）重复子问题->函数头

int pow(x,n)

（2）只关心某一个子问题在做什么事情->函数体的设计
先求出n/2的次方是多少: tmp=pow(x,n/2)
再判断一下n/2能不能整除，不能整除再成上x：return n%2==0?tmp*tmp*x

（3）递归出口
如果n等于0，就返回1

细节问题：

  1. n可能是负数
    要提前把负数转成正数，再用1除一下
    在这里插入图片描述

  2. n可能是-2^31
    -2^31负数太大，转成正数会存不下，int正整数最大是2^31-1
    可以提前把n的类型强转为long long
    在这里插入图片描述

5.2 代码

class Solution {
public:double myPow(double x, int n) {return n<0?1.0/pow(x,-(long long)n):pow(x,n);}double pow(double x, int n){if(n==0)return 1.0;double tmp=pow(x,n/2);return n%2==0?tmp*tmp:tmp*tmp*x; }
};

有问题请指出，大家一起进步！！！

相关文章：

【递归、搜索和回溯】递归、搜索和回溯介绍及递归类算法例题

个人主页 &#xff1a; zxctscl 专栏 【C】、 【C语言】、 【Linux】、 【数据结构】、 【算法】 如有转载请先通知 文章目录 递归、搜索和回溯递归搜索VS 深度优先遍历 VS 深度优先搜索 VS 宽度优先遍历 VS 宽度优先搜索 VS 暴搜回溯与剪枝 1 面试题 08.06. 汉诺塔问题1.1 分析…...

编程日记 2025/8/5 14:51:07

2025最新精选5款3DMAX建筑可视化插件

在3DMAX建筑可视化领域&#xff0c;各类工具如同繁星般璀璨&#xff0c;它们为设计师们搭建起通往理想作品的桥梁。今天&#xff0c;就让我们一同走进几款极具特色的工具——RetailStore插件、2Dto3D插件、DrawFloorPlan插件、MaxToCAD插件以及EXR透视贴图技术&#xff0c;探寻…...

编程日记 2025/7/31 22:59:00

麒麟系统使用-个性化设置

文章目录 前言一、个性化设置-背景二、个性化设置-主题三、个性化设置-锁屏四、个性化设置-屏保五、个性化设置-字体总结 前言 与windows系统相比&#xff0c;麒麟系统中的个性化设置大体相似&#xff0c;在细节上稍有不同。本文将讲述麒麟系统中的个性化设置中的各个模块。 一…...

编程日记 2025/7/31 22:58:59

flask开启https服务支持

目录 一、背景 二、开启https支持 三、自签名 1、安装openssl 2、验证安装 3、自签名 四、编写代码 五、访问https接口 一、背景 最近在做自动化业务&#xff0c;需要兼容现在主流的框架开发的前端页面&#xff0c;于是到github找到了几个项目&#xff0c;clone下来项目并…...

编程日记 2025/7/31 22:58:57

CNN处理图片

In [5]: 123456789101112131415161718192021222324252627282930313233import tensorflow as tf​import matplotlib.pyplot as plt​import numpy as np​​​​# 平滑均值滤波#KaTeX parse error: Expected EOF, got _ at position 14: \text {filter_̲{arg}np.}.full (sha…...

编程日记 2025/7/31 22:58:55

【Bootstrap V4系列】学习入门教程之 组件-表单（Forms）

Bootstrap V4系列 学习入门教程之 组件-表单&#xff08;Forms&#xff09; 表单&#xff08;Forms&#xff09;一、Overview二、Form controls 表单控件2.1 Sizing 尺寸2.2 Readonly 只读2.3 Readonly plain text 只读纯文本 三、Checkboxes and radios 复选框和单选框3.1 Def…...

编程日记 2025/7/31 22:58:53

图像来源：基于协同推理的双视角超声造影分类隐式数据增强方法|文献速递-深度学习医疗AI最新文献

Title 题目 Image by co-reasoning: A collaborative reasoning-based implicit data augmentation method for dual-view CEUS classification 图像来源&#xff1a;基于协同推理的双视角超声造影分类隐式数据增强方法 01 文献速递介绍 结合了B型超声&#xff08;BUS&…...

编程日记 2025/7/31 22:58:51

MySQL性能分析工具：SHOW PROCESSLIST

概述 以下是一份详细的 MySQL SHOW PROCESSLIST 使用教程&#xff0c;帮助您监控和分析数据库当前活动&#xff0c;快速定位性能问题资料已经分类整理好&#xff0c;喜欢的朋友自取&#xff1a;https://pan.quark.cn/s/f52968c518d3 1. 命令基本作用 SHOW PROCESSLIST 显示当…...

编程日记 2025/7/31 22:58:50

Linux网络编程day8本地套接字

本地套接字 利用cs模型实现本地套接字完成进程间通信 对比网络编程TCP C/S模型&#xff0c;注意以下几点 1、int socket(int domain, int type, int protocol); domain-->AF_INET改为AF_UNIX , type都可写SOCK_STREAM/SOCK_DGRAM2、地址结构 sockaddr_in -->sockadd…...

编程日记 2025/7/31 22:58:48

使用 React Native实现鸿蒙开发的详细方案

一、环境准备 1. 基础环境要求 操作系统：Windows 10/11 或 macOS (建议版本最新)Node.js: v16.x 或更高版本npm: v8.x 或更高版本Java JDK: 11 或更高版本DevEco Studio: 3.1 或更高版本 (鸿蒙官方IDE)2. 安装 DevEco Studio 从华为开发者官网下载安装时选择以下组件： Harmo…...

编程日记 2025/7/31 22:58:46

WebRTC流媒体传输协议RTP点到点传输协议介绍，WebRTC为什么使用RTP协议传输音视频流？

通过上一章《WebRTC工作原理详细介绍、WebRTC信令交互过程和WebRTC流媒体传输协议介绍》&#xff0c;我们知道WEBRTC在完成 SDP 协商和 ICE 候选交换信令后&#xff0c;双方就可以建立 RTP 流&#xff0c;开始传输音视频数据&#xff0c;这时&#xff0c;RTP 数据包就通过在 IC…...

编程日记 2025/8/1 5:19:05

【Unity笔记】PathCreator使用教程：用PathCreator实现自定义轨迹动画与路径控制

在Unity开发过程中&#xff0c;角色移动、摄像机动画、轨道系统、AI巡逻等功能中&#xff0c;路径控制是常见又复杂的需求之一。如何优雅、高效地创建路径并控制对象沿路径运动&#xff0c;是游戏开发、动画制作乃至工业仿真中的关键问题。 在这篇文章中&#xff0c;我将介绍一…...

编程日记 2025/7/31 22:58:44

生产安全管理系统标杆

生产安全不容小视&#xff0c;防患于未然是企业安全生产的基石。好的安全预防系统能让隐患产生最初就被扼杀在摇篮里。国内一些好的生产安全防范系统也有很多&#xff0c;今天我们主要介绍一下众联心安这款产品。 安全生产管理,目标制度管理,风险隐患管理,应急安全管理,设备设…...

编程日记 2025/7/31 22:58:42

temu采购自养号全流程解析：从账号搭建到安全下单的技术闭环

temu 自养号采购下单技术是一个精细的过程&#xff0c;需要从多个方面进行考虑和操作&#xff0c;其核心在于通过技术手段模拟真实用户行为&#xff0c;构建独立、安全的账号环境以确保账号的安全性、真实性和采购下单的成功率。以下是对该技术的详细解析 1. 账号准备 手机号…...

编程日记 2025/7/31 22:58:40

MySQl 数据库操作

目录 一、MySQL 数据库介绍 二、MySQl 库操作 1. 系统数据库 2. 数据库操作 &#xff08;1&#xff09;创建数据库 &#xff08;2&#xff09;数据库命名规则 &#xff08;3&#xff09;选择数据库 &#xff08;4&#xff09;查看数据库 &#xff08;5&#xff09;删除…...

编程日记 2025/7/31 22:58:38

OpenHarmony launcher开发——删除dock栏

开发环境 OpenHarmony 5.0.0 代码修改 效果...

编程日记 2025/7/31 22:58:37

zst-2001 历年真题 设计模式

设计模式 - 第1题 a 设计模式 - 第2题 一个产品可以产生多个就是抽象&#xff0c;一个就是工厂 比如这样 第二题a是意图 bc: d 设计模式 - 第3题 b 设计模式 - 第4题 类图里全是builder,疯狂暗示 设计模式 - 第5题 aa 设计模式 - 第6题 只有工厂方法是创…...

编程日记 2025/7/31 22:58:35

Vue3 + Element Plus 动态表单实现

完整代码 <template><div class"dynamic-form-container"><el-formref"dynamicFormRef":model"formData":rules"formRules"label-width"auto"label-position"top"v-loading"loading"&g…...

编程日记 2025/7/31 22:58:33

QML AnimatedImage组件详解

目录 引言相关阅读基础知识&#xff1a;AnimatedImage核心属性与方法工程结构与示例展示工程结构示例1&#xff1a;可控制播放/暂停的AnimatedImage示例2&#xff1a;带进度条的AnimatedImage主界面整合&#xff08;SwipeView滑动展示&#xff09; 总结下载链接 引言 在UI开发…...

编程日记 2025/7/31 22:58:31

Ascend的aclgraph（2）_npu_backend中还有些什么秘密？

1 _npu_backend 文章还是从代码开始 import torch_npu, torchair config torchair.CompilerConfig() # 设置图下沉执行模式 config.mode "reduce-overhead" npu_backend torchair.get_npu_backend(compiler_configconfig) opt_model torch.compile(model, back…...

编程日记 2025/7/31 22:58:29

免布线视频桩：智慧城市停车降本增效的破局利器

在智慧城市建设的进程中&#xff0c;传统停车管理面临成本高、效率低、施工复杂等难题。而视频桩作为创新解决方案&#xff0c;以“免布线、智能化”为核心&#xff0c;正逐步改变这一局面。视频桩通过融合物联网与AI技术&#xff0c;实现自动化监测与数据实时管理&#xff0c;…...

编程日记 2025/8/1 5:19:03

Vulfocus靶场-文件上传-2

monstra 文件上传 &#xff08;CVE-2020-13384&#xff09; Monstra 是一个现代化的轻量级内容管理系统。它易于安装、升级和使用。 Monstra CMS 3.0.4版本中存在着一处安全漏洞&#xff0c;该漏洞源于程序没有正确验证文件扩展名。攻击者可以上传特殊后缀的文件执行任意PHP代…...

编程日记 2025/7/31 21:49:45

nvidia-smi 和 nvcc -V 作用分别是什么？

命令1&#xff1a;nvidia-smi 可以查看当前显卡的驱动版本&#xff0c;以及该驱动支持的CUDA版本。 命令2&#xff1a;nvcc -V 可以看到实际安装的CUDA工具包版本为 12.8 更详细的介绍&#xff0c;可以参考如下链接...

编程日记 2025/7/31 21:49:43

力扣刷题（第二十一天）

灵感来源 - 保持更新&#xff0c;努力学习 - python脚本学习 二叉树的最大深度 解题思路 这道题要求计算二叉树的最大深度&#xff0c;即从根节点到最远叶子节点的最长路径上的节点数。可以使用递归或迭代方法解决&#xff1a; 递归法&#xff08;推荐&#xff09;&#…...

编程日记 2025/7/31 21:49:41

AIOps 工具介绍

AIOps&#xff08;智能运维&#xff09;是通过人工智能技术优化IT运维流程的实践&#xff0c;其核心在于利用机器学习、大数据分析等技术实现运维自动化与智能化。以下从定义、核心价值、技术架构及工具等方面展开说明&#xff1a; 一、AIOps的定义与核心价值 AIOps&#xff0…...

编程日记 2025/7/31 21:49:39

4.3【LLaMA-Factory实战】教育大模型：个性化学习路径生成系统全解析

【LLaMA-Factory实战】教育大模型&#xff1a;个性化学习路径生成系统全解析 一、引言 在教育领域&#xff0c;传统"一刀切"的教学模式难以满足学生的个性化需求。本文基于LLaMA-Factory框架&#xff0c;详细介绍如何构建一个个性化学习路径生成系统&#xff0c;包…...

编程日记 2025/7/31 21:49:37

如何构建容器镜像并将其推送到极狐GitLab容器镜像库？

极狐GitLab 是 GitLab 在中国的发行版&#xff0c;关于中文参考文档和资料有&#xff1a; 极狐GitLab 中文文档极狐GitLab 中文论坛极狐GitLab 官网 构建容器镜像并将其推送到容器镜像库 (BASIC ALL) 在构建和推送容器镜像之前&#xff0c;您必须通过容器镜像库的身份验证。 …...

编程日记 2025/7/31 21:49:34

雷赛伺服L7-EC

1电子齿轮比&#xff1a; 电机圈脉冲1万 &#xff08;pa11的值 x 4倍频&#xff09; 2电机刚性&#xff1a; pa003 或者 0x2003 // 立即生效的 3LED显示&#xff1a; PA5.28 1 电机速度 4精度&#xff1a; PA14 //默认30&#xff0c;超过3圈er18…...

编程日记 2025/7/31 21:49:32

爬虫学习————开始

&#x1f33f;自动化的思想 任何领域的发展原因————“不断追求生产方式的改革&#xff0c;即使得付出与耗费精力越来愈少&#xff0c;而收获最大化”。由此&#xff0c;创造出方法和设备来提升效率。 如新闻的5W原则直接让思考过程规范化、流程化。或者前端框架/后端轮子的…...

编程日记 2025/7/31 21:49:30

Shell 脚本编程详细指南：第五章 - 函数与参数传递

Shell 脚本编程详细指南&#xff1a;第五章 - 函数与参数传递 引言&#xff1a;函数在脚本工程化中的核心价值 函数是Shell脚本实现模块化编程的基石。本章将深入解析函数编程的各个方面&#xff0c;从基础定义到高级应用&#xff0c;助您构建可维护、可重用的脚本架构。我们…...

编程日记 2025/7/31 21:49:28

使用 docker 安装 nacos3.x

一、安装 nacos 1.拉取镜像 使用如下指令拉取镜像 docker pull nacos/nacos-server 拉取完成后&#xff0c;可以使用以下命令查看是否拉取到对应的镜像&#xff0c;默认拉取最新镜像 docker images 2.新建挂载文件目录 mkdir -p /home/ubuntu/nacos/conf/mkdir -p /home/…...

编程日记 2025/7/31 21:49:26

Docker的基础操作

docker是一个用Go语言实现的开源项目&#xff0c;可以让我们方便的创建和使用容器&#xff0c;docker将程序以及程序所有的依赖都打包到docker container&#xff0c;这样你的程序可以在任何环境都会有一致的表现&#xff0c;这里程序运行的依赖也就是容器就好比集装箱&#xf…...

编程日记 2025/7/31 21:49:24

权限控制模型全解析：RBAC、ACL、ABAC 与现代混合方案

权限控制模型全解析&#xff1a;RBAC、ACL、ABAC 与现代混合方案 在企业信息系统、SaaS 应用、安全平台中&#xff0c;权限控制模型是确保用户访问安全和功能隔离的基础架构设计之一。本文将系统性梳理常见的权限控制模型&#xff0c;包括 RBAC、ACL、ABAC、DAC、MAC、ReBAC 等…...

编程日记 2025/7/31 21:49:22

内存安全革命：工具、AI 与政策驱动的 C 语言转型之路

引言 在 CVE-2025-21298 等高危漏洞频发的背景下&#xff0c;内存安全已成为全球软件产业的核心议题。根据 CISA 最新数据&#xff0c;2024 年全球 72% 的网络攻击源于内存安全漏洞&#xff0c;而 C/C 代码贡献了其中 89% 的风险。这一严峻现实催生了技术革新的三重浪潮&#…...

编程日记 2025/7/31 21:49:20

电厂数据库未来趋势：时序数据库 + AI 驱动的自优化系统

在电力行业加速数字化与智能化转型的进程中&#xff0c;电厂数据库作为数据管理与应用的核心枢纽&#xff0c;正经历着深刻变革。时序数据库与 AI 技术的融合&#xff0c;正催生一种全新的自优化系统&#xff0c;为电厂设备全生命周期管理带来前所未有的效能提升与创新机遇。这…...

编程日记 2025/8/1 5:19:01

stm32 debug卡在0x1FFFxxxx

自己画的一个四轴飞机电路板&#xff0c;之前还能debug&#xff0c;改了一下mos管两端的电阻&#xff0c;还能正常下载&#xff0c;蓝牙接收也正常&#xff0c;但是debug出问题了&#xff0c;刚下载就自动运行&#xff0c;然后程序就在0x1FFFxxxx附近循环运行&#xff0c;这一块…...

编程日记 2025/8/1 5:18:59

什么是AI写作

一、AI写作简介 AI 写作正在成为未来 10 年最炙手可热的超级技能。已经有越来越多的人通过 AI 写作&#xff0c;在自媒体、公文写作、商业策划等领域实现了提效&#xff0c;甚至产生了变现收益。 掌握 AI 写作技能&#xff0c;不仅能提高个人生产力&#xff0c;还可能在未来的 …...

编程日记 2025/8/1 5:18:57

港大今年开源了哪些SLAM算法？

过去的5个月&#xff0c;香港大学 MaRS 实验室陆续开源了四套面向无人机的在线 SLAM 框架&#xff1a;**FAST-LIVO2 、Point-LIO&#xff08;grid-map 分支&#xff09; 、Voxel-SLAM 、Swarm-LIO2 **。这四套框架覆盖了单机三传感器融合、高带宽高速机动、长时间多级地图优化以…...

编程日记 2025/8/1 5:18:55

PostgreSQL 表空间占用分析与执行计划详解

PostgreSQL 表空间占用分析与执行计划详解 引言 在数据库管理和优化中&#xff0c;了解表占用的空间大小以及查询的执行计划是至关重要的。本文将详细介绍如何在 PostgreSQL 中查看普通表和分区表的空间占用情况&#xff0c;以及如何分析和解读执行计划。 一、查看表空间占用 …...

编程日记 2025/8/1 5:18:53

robotframe启动ride.py

我的双击ride.py会自动用pycharm打开&#xff0c;变成代码文件 解决方法&#xff1a;定位到ride.py所在文件夹&#xff08;在anaconda的scripts里面&#xff09;&#xff0c;文件夹上方输入cmd 再输入该命令即可...

编程日记 2025/8/1 5:18:51

通过Linux系统服务管理IoTDB集群的高效方法

IoTDB是一款专为工业物联网领域设计的高性能时间序列数据库。在生产环境中&#xff0c;确保IoTDB集群的稳定运行至关重要。本文将介绍如何利用Linux系统服务来管理IoTDB集群&#xff0c;以实现高效的启动、监控和自动重启。 一、基本配置与环境需求 为了解决传统IoTDB启动方式…...

编程日记 2025/8/1 5:18:49

机器学习-数据集划分和特征工程

一.数据集划分 API函数&#xff1a; sklearn.model_selection.train_test_split(*arrays&#xff0c;**options) 参数&#xff1a; - arrays&#xff1a;多个数组&#xff0c;可以是列表&#xff0c;numpy数组&#xff0c;也可以是dataframe数据框等 - options&#xff1a;&…...

编程日记 2025/8/1 5:18:48

LDO与DCDC总结

目录 1. 工作原理 2. 性能对比 3. 选型关键因素 4. 典型应用 总结 1. 工作原理 LDO LDO通过线性调节方式实现降压&#xff0c;输入电压需略高于输出电压&#xff08;压差通常为0.2-2V&#xff09;&#xff0c;利用内部PMOS管或PNP三极管调整压差以稳定输出电压。其结构简单…...

编程日记 2025/8/1 5:18:46

5 种距离算法总结！！

大家好&#xff01;我是 我不是小upper&#xff5e; 今天&#xff0c;咱们聚焦一个在机器学习领域极为关键、在实际项目中也高频使用的主题 ——距离算法。在机器学习的世界里&#xff0c;距离算法就像是一把 “度量尺”&#xff0c;专门用来衡量数据点之间的相似性或差异性。…...

编程日记 2025/8/1 5:18:44

【leetcode100】最长重复子数组

1、题目描述 给两个整数数组 nums1 和 nums2 &#xff0c;返回 两个数组中 公共的 、长度最长的子数组的长度 。 示例 1&#xff1a; 输入&#xff1a;nums1 [1,2,3,2,1], nums2 [3,2,1,4,7] 输出&#xff1a;3 解释&#xff1a;长度最长的公共子数组是 [3,2,1] 。示例 2&…...

编程日记 2025/8/1 5:18:42

独立自主的网络浏览器——Ladybird

独立自主的网络浏览器——Ladybird 随着互联网技术的飞速发展&#xff0c;浏览器作为人们探索网络世界的窗口&#xff0c;其技术创新和安全措施至关重要。然而&#xff0c;市场上绝大多数浏览器都是基于现有的成熟引擎进行开发&#xff0c;如何创新突破&#xff0c;成为一个独…...

编程日记 2025/8/1 5:18:40

强化学习三大基本方法-DP、MC、TD

强化学习进阶 本文主要讲解 动态规划法&#xff08;Dynamic Programming DP&#xff09;蒙特卡洛法&#xff08;Monte Carlo MC&#xff09;时序差分法&#xff08;Temporal Difference TD&#xff09; 1. 动态规划法 1.1 动态规划概念 动态规划核心思想&#xff1a; 其核心…...

编程日记 2025/8/1 5:18:38

【数据结构】1. 时间/空间复杂度

- 第 95 篇 - Date: 2025 - 05 - 09 Author: 郑龙浩/仟墨 【数据结构 】 文章目录 数据结构 - 1 -了解数据结构与算法1 什么是数据结构2 什么是算法3 数据结构的重要性&#xff1f; 一 时间复杂度_空间复杂度1 时间复杂度① 表示方法② 推导大 O 的规则:③ **代码示例 ** 2 空…...

编程日记 2025/8/1 5:18:36

k8s存储类型：emptyDir、hostPath、nfs、pvc及存储类storageclass的静态/动态创建pv

Kubernetes存储类型详解 Kubernetes&#xff08;K8s&#xff09;提供了多种存储类型&#xff0c;满足不同的存储需求。这些存储类型包括 emptyDir、hostPath、nfs、PersistentVolumeClaim&#xff08;PVC&#xff09;以及存储类&#xff08;StorageClass&#xff09;的静态和动…...

编程日记 2025/8/1 3:06:23

TRAE 配置blender MCP AI自动3D建模

BlenderMCP - Blender模型上下文协议集成 BlenderMCP通过模型上下文协议(MCP)将Blender连接到Claude AI&#xff0c;允许Claude直接与Blender交互并控制Blender。这种集成实现了即时辅助的3D建模、场景创建和操纵。 1.第一步下载 MCP插件(addon.py):Blender插件&#xff0c;在…...

编程日记 2025/8/1 3:06:21