当前位置：首页 > news >正文

Transformer数学推导——Q56 推导动态残差门控（Dynamic Residual Gating）的权重更新公式

news 来源：原创 2025/8/21 14:43:09

该问题归类到Transformer架构问题集——残差与归一化——残差连接。请参考LLM数学推导——Transformer架构问题集。

1. 引言

在深度学习的演进历程中，网络结构的创新始终围绕着如何更高效地处理信息、提升模型性能展开。动态残差门控（Dynamic Residual Gating）犹如一位智慧的 “信息调度师”，打破传统残差连接的固定模式，为神经网络中信息的传递与融合带来了全新的思路。它能够依据输入信息的特征动态调整信息的流动路径，使得网络在学习过程中更加灵活高效。而权重更新公式作为动态残差门控发挥作用的核心机制，就像是这位 “信息调度师” 的 “操作指南”，决定了其如何精准调控。深入推导这一公式，不仅能从理论层面揭示动态残差门控的工作原理，更能为其在实际应用中，尤其是在大型语言模型（LLM）等复杂场景下的优化与改进提供坚实的依据。接下来，我们将逐步揭开动态残差门控权重更新公式的神秘面纱。

2. 动态残差门控的基本概念

2.1 什么是动态残差门控

想象神经网络是一座庞大复杂的信息大厦，传统残差连接如同固定的直梯，为信息在楼层（网络层）间传递提供了便捷通道。而动态残差门控则更像配备智能门禁系统的电梯，这个 “智能门” 由门控函数 g(x) 掌控，它依据输入 x 的 “身份特征”，动态决定信息通过的比例。在动态残差门控结构中，输出 y 的计算方式为 $y = g(x) \cdot F(x) + (1 - g(x)) \cdot x$ 。其中，x 是输入信息，F(x) 是经过该层变换后的信息，g(x) 是关键的门控函数，其取值范围在 [0, 1] 之间。当 g(x) 趋近于 1 时，就如同大门大开，大量经过变换的信息 F(x) 涌入输出；当 g(x) 趋近于 0 时，则更多保留原始输入 x 的信息，实现了信息的动态筛选与融合。

2.2 门控函数的作用

门控函数 g(x) 堪称动态残差门控的 “灵魂”，它像一位经验丰富的 “安检员”，对输入信息进行细致评估。在深度学习训练过程中，不同类型、不同阶段的输入信息价值各异。对于一些包含丰富有效特征的输入，门控函数会调高 g(x) 的值，让网络充分利用变换后的信息进行特征提取与学习；而当输入信息可能存在噪声或与当前任务关联度低时，门控函数会降低 g(x) 的值，更多保留原始信息，避免网络被误导。例如在图像识别任务中，面对清晰且特征明显的图像区域，门控函数会鼓励网络对其进行深度变换学习；对于模糊或干扰区域，则适当保留原始信息，确保网络决策的稳健性。

3. 推导权重更新公式的准备工作

3.1 定义损失函数

为了引导动态残差门控网络学习，我们需要一个 “评判标准”，即损失函数 L 。它如同一位 “严格的考官”，衡量网络预测结果与真实标签之间的差异。根据任务类型不同，损失函数的选择也有所差异，如回归任务常用均方误差损失，分类任务则多采用交叉熵损失。这里我们以通用损失函数 $L(y, \hat{y})$ 为例，其中 y 是网络实际输出， $\hat{y}$ 是真实标签。损失函数值越低，表明网络预测越准确，我们的目标就是通过调整网络参数，让损失函数尽可能小。

3.2 门控函数的具体形式

通常，门控函数 $g(x)$ 由一个小型神经网络实现，常见结构是全连接层搭配 sigmoid 激活函数。设门控函数参数为 $\theta_g$ ，则 $g(x) = \sigma(W_g x + b_g)$ ，其中 $W_g$ 是权重矩阵，负责对输入 x 进行加权变换； $b_g$ 是偏置向量，为加权结果添加偏移量； $\sigma$ 是 sigmoid 函数，其表达式为 $\sigma(z) = \frac{1}{1 + e^{-z}}$ ，该函数能将输入映射到 [0, 1] 区间，满足门控函数的取值要求。

3.3 变换函数 F(x) 的参数

变换函数 F(x) 承担着对输入信息进行特征变换的重要职责，其参数 $\theta_F$ 决定了变换的方式和效果。 $\theta_F$ 可以是卷积层的权重（在处理图像等数据时）、全连接层的权重（常用于特征映射与分类）等。在网络训练中，我们要通过调整 $\theta_g$ 和 $\theta_F$ ，使网络性能达到最优，而推导它们的权重更新公式就是实现这一目标的关键步骤。

4. 推导权重更新公式的过程

4.1 计算损失函数关于门控函数参数 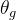$\theta_g$ 的梯度

我们借助链式法则来计算 $\frac{\partial L}{\partial \theta_g}$ ，这一过程如同沿着一条由多个环节组成的链条，逐步追溯损失函数对门控函数参数的影响。根据链式法则， $\frac{\partial L}{\partial \theta_g} = \frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial g(x)} \cdot \frac{\partial g(x)}{\partial \theta_g}$ 。

计算 $\frac{\partial L}{\partial y}$ ：这是损失函数关于网络输出 y 的梯度，反映了损失函数随输出 y 变化的敏感程度。不同损失函数的 $\frac{\partial L}{\partial y}$ 计算方式不同，以交叉熵损失函数为例，其求导结果会根据具体的输出和标签形式确定，它是后续计算的基础。
计算 $\frac{\partial y}{\partial g(x)}$ ：对 $y = g(x) \cdot F(x) + (1 - g(x)) \cdot x$ 关于 g(x) 求导，将 F(x) 和 x 看作常数，根据求导公式可得 $\frac{\partial y}{\partial g(x)} = F(x) - x$ ，该梯度体现了输出 y 对门控函数 g(x) 的依赖关系。
计算 $\frac{\partial g(x)}{\partial \theta_g}$ ：由于 $g(x) = \sigma(W_g x + b_g)$ ，先对 sigmoid 函数求导， $\sigma'(z) = \sigma(z)(1 - \sigma(z))$ ，再根据链式法则， $\frac{\partial g(x)}{\partial W_g} = \sigma'(W_g x + b_g) \cdot x^T$ ， $\frac{\partial g(x)}{\partial b_g} = \sigma'(W_g x + b_g)$ 。综合上述三个梯度的计算结果，就能得到 $\frac{\partial L}{\partial \theta_g}$ ，明确损失函数对门控函数参数的影响方向和程度。

4.2 计算损失函数关于变换函数参数 $\theta_F$ 的梯度

同样运用链式法则， $\frac{\partial L}{\partial \theta_F} = \frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial F(x)} \cdot \frac{\partial F(x)}{\partial \theta_F}$ 。

计算 $\frac{\partial y}{\partial F(x)}$ ：对 $y = g(x) \cdot F(x) + (1 - g(x)) \cdot x$ 关于 F(x) 求导，把 g(x) 和 x 视为常数，可得 $\frac{\partial y}{\partial F(x)} = g(x)$ ，该梯度表明了输出 y 对变换函数 F(x) 的依赖程度受门控函数 g(x) 的影响。
计算 $\frac{\partial F(x)}{\partial \theta_F}$ ： $\frac{\partial F(x)}{\partial \theta_F}$ 的计算取决于 F(x) 的具体形式。若 F(x) 是卷积层，根据卷积运算的求导规则计算梯度；若为全连接层，则依据全连接层的求导方式得出结果。将这三个梯度相乘，就能得到 $\frac{\partial L}{\partial \theta_F}$ ，确定损失函数对变换函数参数的影响。

4.3 权重更新公式

在获取 $\frac{\partial L}{\partial \theta_g}$ 和 $\frac{\partial L}{\partial \theta_F}$ 后，我们采用梯度下降法进行权重更新。梯度下降法的核心思想是沿着梯度的反方向调整权重，使损失函数逐渐减小，就像顺着山坡向下走以寻找最低点一样。对于门控函数参数 $\theta_g$ ，更新公式为 $\theta_g^{new} = \theta_g^{old} - \alpha \frac{\partial L}{\partial \theta_g}$ ；对于变换函数参数 $\theta_F$ ，更新公式为 $\theta_F^{new} = \theta_F^{old} - \alpha \frac{\partial L}{\partial \theta_F}$ 。其中， $\alpha$ 是学习率，它控制着每次权重更新的步长。学习率过大，权重更新步伐迈得太大，可能导致网络在训练过程中 “跳过” 最优解，无法收敛；学习率过小，网络学习速度会极为缓慢，耗费大量时间和计算资源。因此，合理选择学习率至关重要。

5. 动态残差门控在 LLM 中的使用

5.1 在 Transformer 架构中的融入

当前主流的 LLM 大多基于 Transformer 架构，动态残差门控可巧妙融入其中。在 Transformer 的编码器和解码器部分，每一层都包含多头自注意力机制和前馈神经网络。将动态残差门控应用于这些层之间，门控函数 g(x) 能够根据输入文本的语义特征、上下文信息等，动态调节信息传递。例如，当处理一段逻辑复杂、语义丰富的文本时，门控函数会根据文本中关键词、句子结构等信息，调高 g(x) 值，让经过自注意力机制和前馈神经网络变换后的信息更多地参与到后续层的计算中，帮助模型深入理解文本语义；而当遇到一些重复、冗余或与核心内容关联度低的文本片段时，门控函数会降低 g(x) 值，保留更多原始输入信息，避免模型被无效信息干扰，从而更高效地提取关键语义信息。

5.2 实际应用案例 ——GPT 系列模型的优化

以 GPT 系列模型为例，在训练过程中，随着网络层数的不断增加，如何有效传递和融合各层信息成为提升模型性能的关键。通过引入动态残差门控，模型能够更好地处理长文本序列。在生成文本时，对于前文已经提及且重要的信息，门控函数可以通过调整权重，让这些信息更顺畅地传递到后续生成层，确保生成的文本在语义和逻辑上与前文连贯一致。例如，在续写一个故事时，对于故事中已经设定的人物性格、情节线索等重要信息，动态残差门控能够使相关信息在各层之间高效流动，帮助模型生成符合故事发展逻辑的后续内容，提升文本生成的质量和连贯性。同时，在面对输入文本中的噪声或错误信息时，门控机制也能发挥作用，减少这些不良信息对模型输出的影响，增强模型的鲁棒性。

5.3 对模型性能的提升效果

在实际应用中，动态残差门控在 LLM 上的应用显著提升了模型性能。通过实验对比发现，采用动态残差门控的 LLM 在多种自然语言处理任务，如文本生成、问答系统、机器翻译等方面，相比未使用该技术的模型，在准确率、连贯性、语义合理性等指标上均有明显提升。在文本生成任务中，生成的文本更加流畅自然，逻辑更加严密；在问答系统中，能够更准确地理解问题意图，给出更精准的答案；在机器翻译任务中，翻译结果在语法和语义上更符合目标语言习惯。这些成果充分证明了动态残差门控在 LLM 中对于优化信息融合、提升模型性能的重要价值。

6. 代码示例与解读

import torch
import torch.nn as nn
import torch.optim as optim# 定义门控函数
class GatingFunction(nn.Module):def __init__(self, input_size):super(GatingFunction, self).__init__()self.fc = nn.Linear(input_size, 1)self.sigmoid = nn.Sigmoid()def forward(self, x):return self.sigmoid(self.fc(x))# 定义变换函数
class TransformationFunction(nn.Module):def __init__(self, input_size, output_size):super(TransformationFunction, self).__init__()self.fc = nn.Linear(input_size, output_size)def forward(self, x):return self.fc(x)# 定义动态残差门控模块
class DynamicResidualGating(nn.Module):def __init__(self, input_size):super(DynamicResidualGating, self).__init__()self.gating = GatingFunction(input_size)self.transformation = TransformationFunction(input_size, input_size)def forward(self, x):g = self.gating(x)F_x = self.transformation(x)return g * F_x + (1 - g) * x# 模拟输入数据和真实标签
input_size = 10
batch_size = 16
x = torch.randn(batch_size, input_size)
y_true = torch.randn(batch_size, input_size)# 初始化动态残差门控模块
model = DynamicResidualGating(input_size)# 定义损失函数和优化器
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)# 训练过程
for epoch in range(100):optimizer.zero_grad()y_pred = model(x)loss = criterion(y_pred, y_true)loss.backward()optimizer.step()if (epoch + 1) % 10 == 0:print(f'Epoch {epoch + 1}, Loss: {loss.item()}')

6.1 代码解读

门控函数实现：GatingFunction 类构建了门控函数，通过全连接层 fc 对输入进行线性变换，再经 sigmoid 函数将输出压缩到 [0, 1] 区间，生成门控值 g(x) ，为后续信息融合提供控制信号。
变换函数实现：TransformationFunction 类定义的变换函数由全连接层构成，对输入 x 进行特征变换，得到 F(x) ，实现信息的初步处理与转换。
动态残差门控模块实现：DynamicResidualGating 类整合门控函数和变换函数，在 forward 方法中，先计算门控值 g 和变换后的 $F_x$ ，再依据动态残差门控公式 $y = g \cdot F_x + (1 - g) \cdot x$ 完成信息融合，输出最终结果。
训练过程：模拟输入数据 x 和真实标签 y_true ，初始化动态残差门控模型 model 。选用均方误差损失函数 criterion 衡量预测与真实值差异，随机梯度下降优化器 optimizer 更新模型参数。在训练循环中，每次迭代先清零梯度，进行前向传播计算预测值 y_pred ，计算损失后反向传播求梯度，最后更新参数，并定期打印损失值，以便观察模型训练进程与性能变化。

7. 总结与展望

通过对动态残差门控权重更新公式的深度推导，以及在 LLM 中的应用分析，我们全面揭示了这一技术的核心原理与实践价值。从理论推导层面，明确了门控函数和变换函数参数如何依据损失函数梯度进行更新，为网络训练提供了精确的指导；在 LLM 应用方面，展示了动态残差门控如何优化信息流动，提升模型在自然语言处理任务中的性能。

然而，这一技术仍有广阔的发展空间。未来研究可探索如何进一步优化门控函数的设计，使其能更精准地捕捉输入信息的复杂特征，实现更高效的信息筛选与融合；也可尝试将动态残差门控与其他先进技术，如注意力机制的变体、强化学习等相结合，创造出更强大的网络架构。此外，在实际应用中，如何根据不同的 LLM 任务和数据特点，自适应地调整动态残差门控的参数和结构，也是值得深入研究的方向。相信随着研究的不断深入，动态残差门控将在深度学习领域发挥更大的作用，推动 LLM 等技术迈向新的高度。