当前位置：首页 > news >正文

《Python星球日记》第36天：线性代数基础

news 来源：原创 2025/8/21 14:45:03

名人说：路漫漫其修远兮，吾将上下而求索。—— 屈原《离骚》
创作者：Code_流苏(CSDN)（一个喜欢古诗词和编程的Coder😊）
专栏：《Python星球日记》，限时特价订阅中ing

目录

一、标量、向量、矩阵的基本概念
1. 标量
2. 向量
3. 矩阵

二、矩阵运算
1. 矩阵加法
2. 矩阵乘法
3. 矩阵转置
4. 逆矩阵

三、向量空间与线性组合
1. 向量空间的概念
2. 线性组合
3. 线性独立性

四、NumPy 实践：矩阵运算
1. NumPy 基础
2. 使用 NumPy 进行矩阵运算
3. 实战示例：使用NumPy解线性方程组

总结与展望

👋 专栏介绍： Python星球日记专栏介绍（持续更新ing）
✅ 上一篇：《Python星球日记》第35天：全栈开发（综合项目）

欢迎来到Python星球的第36天！🪐

在前面我们学习了Python基础、爬虫、数据可视化，并深入了解了Web开发。今天，我们将探索线性代数基础，这是数据科学和机器学习领域的重要基石。无论是图像处理、推荐系统还是神经网络，线性代数都是不可或缺的数学工具。让我们一起踏上这段数学之旅！

在这里插入图片描述

一、标量、向量、矩阵的基本概念

在线性代数中，我们首先需要理解三个基本概念：标量、向量和矩阵。这些是构建整个线性代数体系的基础元素。

1. 标量

标量（Scalar）是最简单的数学对象，它就是一个单独的数字。

比如：5、-3、0.5、π 等都是标量。在Python中，我们可以用常规的数值类型来表示标量：

# 标量示例
a = 5       # 整数类型标量
b = 3.14    # 浮点类型标量
c = 2 + 3j  # 复数类型标量

2. 向量

向量（Vector）是有序的数字集合，可以看作是一个一维数组。向量可以表示为行向量（横排）或列向量（竖排）。

在这里插入图片描述

在Python中，我们通常使用NumPy库中的array或vector来表示向量：


import numpy as np# 创建向量
column_vector = np.array([[1], [2], [3]])  # 列向量 - 形状为(3,1)
row_vector = np.array([4, 5, 6])           # 行向量 - 形状为(3,)print(column_vector)
print(row_vector)

在这里插入图片描述

向量可以表示空间中的方向和大小，如位置、速度或力，也可以表示数据集中的特征集合。

3. 矩阵

矩阵（Matrix）是二维数字表格，可以看作是向量的集合。矩阵由行和列组成，通常用大写字母表示（如A、B等）。
在这里插入图片描述

矩阵的维度由其行数和列数决定。一个有m行n列的矩阵称为m×n矩阵。

在Python中，使用NumPy创建矩阵非常简单：

import numpy as np# 创建2×3矩阵
A = np.array([[1, 2, 3],[4, 5, 6]])print(A)
print(f"矩阵维度: {A.shape}")  # 输出: (2, 3)

在这里插入图片描述

矩阵在数据科学和机器学习中应用广泛，例如：

图像处理中的图像就是像素矩阵
社交网络中的连接关系可用邻接矩阵表示
推荐系统中的用户-物品评分矩阵

二、矩阵运算

矩阵的基本运算包括加法、乘法、转置和求逆。让我们逐一了解这些操作并用NumPy实现。

1. 矩阵加法

矩阵加法的规则很简单：相同位置的元素相加。两个矩阵必须具有相同的维度才能相加。

在这里插入图片描述

NumPy实现矩阵加法非常直观：

import numpy as np# 创建两个2×2矩阵
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])# 矩阵加法
C = A + Bprint(f"矩阵A:\n{A}")
print(f"矩阵B:\n{B}")
print(f"A + B =\n{C}")  # 输出: [[6 8], [10 12]]

在这里插入图片描述

矩阵加法满足交换律和结合律：A + B = B + A 以及 (A + B) + C = A + (B + C)。

2. 矩阵乘法

矩阵乘法比加法复杂，有两种主要类型：

点乘（element-wise multiplication）：对应位置的元素相乘
矩阵乘法（matrix multiplication）：遵循特定的数学规则

矩阵乘法要求第一个矩阵的列数等于第二个矩阵的行数。假设矩阵A的维度是m×n，矩阵B的维度是n×p，那么A×B的结果是一个m×p的矩阵。

在这里插入图片描述

NumPy中实现矩阵乘法有多种方式：

import numpy as np# 创建矩阵
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])# 点乘（元素相乘）
C_elementwise = A * B
print(f"点乘结果:\n{C_elementwise}")  # 输出: [[5 12], [21 32]]# 矩阵乘法
C_matmul = np.matmul(A, B)  # 或使用 A @ B (Python 3.5+)
print(f"矩阵乘法结果:\n{C_matmul}")  # 输出: [[19 22], [43 50]]# 使用 dot 函数
C_dot = A.dot(B)
print(f"使用dot函数的结果:\n{C_dot}")  # 输出与C_matmul相同

在这里插入图片描述

矩阵乘法不满足交换律：通常情况下，A×B ≠ B×A。这是初学者容易犯的一个错误。

3. 矩阵转置

矩阵的转置是指将矩阵的行和列互换。如果A是一个m×n矩阵，那么它的转置A^T是一个n×m矩阵。

在这里插入图片描述

在NumPy中，转置操作非常简单：

import numpy as np# 创建2×3矩阵
A = np.array([[1, 2, 3],[4, 5, 6]])# 转置矩阵
A_T = A.T  # 或使用 np.transpose(A)print(f"原矩阵A:\n{A}")
print(f"转置后A^T:\n{A_T}")

在这里插入图片描述

矩阵转置的一些重要性质：

(A^T)T = A（转置的转置等于原矩阵）
(A + B)^T = A^T + B^T（转置分配律）
(AB)^T = B^T A^T（转置的乘法顺序会反转）

4. 逆矩阵

逆矩阵是线性代数中的一个重要概念。只有方阵（行数等于列数的矩阵）才可能有逆矩阵。

如果矩阵A的逆矩阵存在，记为A^(-1)，则有：A × A^(-1) = A^(-1) × A = I，其中I是单位矩阵（对角线上元素为1，其他元素为0）。

在这里插入图片描述

在NumPy中，可以使用np.linalg.inv()函数求矩阵的逆：

import numpy as np# 创建可逆矩阵
A = np.array([[4, 7], [2, 6]])# 计算逆矩阵
try:A_inv = np.linalg.inv(A)print(f"矩阵A:\n{A}")print(f"A的逆矩阵:\n{A_inv}")# 验证 A × A^(-1) = II = np.dot(A, A_inv)print(f"A × A^(-1) =\n{np.round(I, decimals=10)}")  # 使用round处理浮点误差
except np.linalg.LinAlgError:print("矩阵不可逆")

在这里插入图片描述

需要注意的是，并非所有矩阵都有逆矩阵。如果矩阵的行列式为0，那么它没有逆矩阵，被称为奇异矩阵或不可逆矩阵。

逆矩阵在解线性方程组和机器学习中非常重要，比如在线性回归中求解系数时就需要用到。

三、向量空间与线性组合

1. 向量空间的概念

向量空间是包含向量的集合，该集合对向量加法和标量乘法运算封闭。简单来说，向量空间是一组向量，且任意两个向量的和以及任意向量与标量的积仍然属于该空间。

在这里插入图片描述

最常见的向量空间是欧几里得空间，如二维平面R²或三维空间R³。

2. 线性组合

线性组合是向量空间的一个核心概念。一组向量的线性组合是指将这些向量乘以标量系数后相加。

形式上，向量v₁, v₂, …, vₙ的线性组合可表示为：c₁v₁ + c₂v₂ + … + cₙvₙ

其中c₁, c₂, …, cₙ是标量系数。

通过线性组合，我们可以用少量的基础向量生成整个向量空间。例如，在二维空间中，任何向量都可以表示为标准基向量i = [1, 0]和j = [0, 1]的线性组合。

import numpy as np
import matplotlib.pyplot as plt# 设置中文字体支持
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False# 标准基向量
e1 = np.array([1, 0])  # i 向量
e2 = np.array([0, 1])  # j 向量# 任意向量作为线性组合
v = np.array([3, 2])   # 3i + 2j# 可视化
plt.figure(figsize=(8, 6))
plt.axhline(y=0, color='k', linestyle='-', alpha=0.3)
plt.axvline(x=0, color='k', linestyle='-', alpha=0.3)
plt.arrow(0, 0, e1[0], e1[1], head_width=0.1, head_length=0.1, fc='blue', ec='blue', label='e1')
plt.arrow(0, 0, e2[0], e2[1], head_width=0.1, head_length=0.1, fc='green', ec='green', label='e2')
plt.arrow(0, 0, v[0], v[1], head_width=0.1, head_length=0.1, fc='red', ec='red', label='v=3e1+2e2')
plt.grid(True, alpha=0.3)
plt.xlim(-0.5, 4)
plt.ylim(-0.5, 3)
plt.legend()
plt.title('向量的线性组合示例')
plt.show()

在这里插入图片描述

3. 线性独立性

向量集合{v₁, v₂, …, vₙ}如果满足：c₁v₁ + c₂v₂ + … + cₙvₙ = 0只有当所有c₁ = c₂ = … = cₙ = 0时成立，那么这组向量就是线性独立的。

换句话说，线性独立意味着集合中的任何向量都不能表示为其他向量的线性组合。

在这里插入图片描述

在NumPy中，我们可以用以下方法检查向量是否线性独立，通常通过计算矩阵的秩（rank）：

import numpy as np# 创建向量集合
v1 = np.array([1, 0, 0])
v2 = np.array([0, 1, 0])
v3 = np.array([1, 1, 0])  # v3 = v1 + v2，所以是线性相关的# 将向量作为矩阵的行
matrix = np.vstack((v1, v2, v3))# 计算矩阵的秩
rank = np.linalg.matrix_rank(matrix)# 判断线性独立性
n_vectors = matrix.shape[0]  # 向量数量
if rank == n_vectors:print("这些向量是线性独立的")
else:print("这些向量是线性相关的")print(f"秩 = {rank}，向量数量 = {n_vectors}")

在这里插入图片描述

线性独立性的概念在许多领域都很重要：

在机器学习中，特征选择就是要找到线性独立的特征集合
在主成分分析（PCA）中，我们寻找数据的主成分，这些主成分是线性独立的
在解线性方程组时，判断方程组是否有唯一解

四、NumPy 实践：矩阵运算

现在让我们通过一系列实际的Python代码示例，巩固对线性代数的理解。

1. NumPy 基础

NumPy是Python中进行科学计算的基础库，提供了强大的多维数组对象和处理这些数组的工具。

import numpy as np# 创建数组
a = np.array([1, 2, 3])                # 一维数组
b = np.array([[1, 2, 3], [4, 5, 6]])   # 二维数组# 一些基本操作
print(f"数组b的形状: {b.shape}")        # (2, 3)
print(f"数组b的维度: {b.ndim}")         # 2
print(f"数组b的元素类型: {b.dtype}")    # int64
print(f"数组b的元素总数: {b.size}")     # 6# 创建特殊矩阵
eye = np.eye(3)                        # 3×3单位矩阵
zeros = np.zeros((2, 3))               # 2×3全零矩阵
ones = np.ones((2, 2))                 # 2×2全一矩阵
random_matrix = np.random.rand(2, 3)    # 2×3随机矩阵print(f"单位矩阵:\n{eye}")

在这里插入图片描述

2. 使用 NumPy 进行矩阵运算

让我们实现前面讨论过的矩阵运算：

import numpy as np# 创建样例矩阵
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])# 1. 矩阵加法
C_add = A + B
print(f"矩阵加法 A + B =\n{C_add}")# 2. 矩阵乘法
C_mul = A @ B  # 或 np.matmul(A, B) 或 A.dot(B)
print(f"矩阵乘法 A × B =\n{C_mul}")# 3. 矩阵转置
A_T = A.T
print(f"矩阵A的转置 =\n{A_T}")# 4. 矩阵的逆（如果存在）
try:A_inv = np.linalg.inv(A)print(f"矩阵A的逆 =\n{A_inv}")# 验证 A × A^(-1) = II_check = A @ A_invprint(f"A × A^(-1) =\n{np.round(I_check, decimals=10)}")
except np.linalg.LinAlgError as e:print(f"错误: {e}")# 5. 求矩阵的行列式
det_A = np.linalg.det(A)
print(f"矩阵A的行列式 = {det_A}")# 6. 求矩阵的特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(A)
print(f"矩阵A的特征值 = {eigenvalues}")
print(f"矩阵A的特征向量 =\n{eigenvectors}")

在这里插入图片描述

3. 实战示例：使用NumPy解线性方程组

线性代数的一个重要应用是解线性方程组。例如，解方程组：

2x + y = 8
3x + 5y = 19

可以表示为矩阵形式：AX = B，其中A是系数矩阵，X是未知数向量，B是常数向量。

import numpy as np# 定义系数矩阵A和常数向量B
A = np.array([[2, 1], [3, 5]])
B = np.array([8, 19])# 方法1：使用矩阵的逆
# X = A^(-1) × B
X1 = np.linalg.inv(A).dot(B)
print(f"使用矩阵的逆解得: x = {X1[0]}, y = {X1[1]}")# 方法2：使用numpy的线性代数解法函数
X2 = np.linalg.solve(A, B)
print(f"使用linalg.solve解得: x = {X2[0]}, y = {X2[1]}")# 验证解是否正确
verification = A @ X2
print(f"验证: A × X = {verification}，应等于B = {B}")

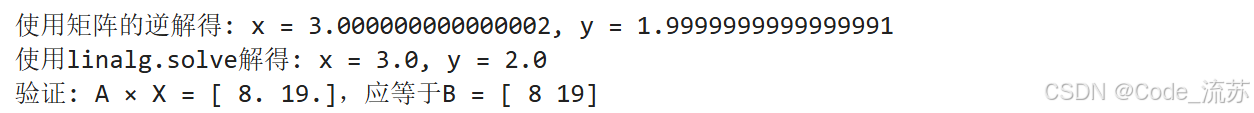
在这里插入图片描述

这个例子展示了如何将实际问题转化为线性代数问题并使用NumPy求解。这种方法在数据科学、机器学习和科学计算中应用广泛。

总结与展望

今天，我们学习了线性代数的基础知识，包括标量、向量和矩阵的概念，矩阵的基本运算（加法、乘法、转置和求逆），以及向量空间和线性组合的概念。我们还通过NumPy实现了这些操作，并展示了如何应用线性代数解决实际问题。

线性代数是机器学习和数据科学的重要基础。在未来的学习中，你会发现这些知识对于理解以下内容至关重要：

机器学习算法，如线性回归、主成分分析（PCA）和支持向量机（SVM）
深度学习中的矩阵运算和梯度下降
计算机图形学中的变换矩阵
优化问题的数学建模和求解

下一步，你可以深入学习更多线性代数概念，以及它们在实际应用中的角色。

今天的知识是我们探索数据科学和人工智能宇宙的第一步，未来我们将继续这段Python星球探索之旅！

通过这篇文章，你已经掌握了线性代数的基础知识和NumPy的矩阵操作。试着自己实现一些示例，加深对概念的理解。线性代数不仅仅是抽象的数学，它是解决现实问题的强大工具！

创作者：Code_流苏(CSDN)（一个喜欢古诗词和编程的Coder😊）
如果你对今天的内容有任何问题，或者想分享你的学习心得，欢迎在评论区留言讨论！

目录

一、标量、向量、矩阵的基本概念

1. 标量

2. 向量

3. 矩阵

二、矩阵运算

1. 矩阵加法

2. 矩阵乘法

3. 矩阵转置

4. 逆矩阵

三、向量空间与线性组合

1. 向量空间的概念

2. 线性组合

3. 线性独立性

四、NumPy 实践：矩阵运算

1. NumPy 基础

2. 使用 NumPy 进行矩阵运算

3. 实战示例：使用NumPy解线性方程组

总结与展望

相关文章：