当前位置：首页 > news >正文

人工智能数学基础（六）：数理统计

news 来源：原创 2025/5/17 21:22:09

数理统计是人工智能中数据处理和分析的核心工具，它通过收集、分析数据来推断总体特征和规律。本文将系统介绍数理统计的基本概念和方法，并结合 Python 实例，帮助读者更好地理解和应用这些知识。资源绑定附上完整资源供读者参考学习！

6.1 概述

6.1.1 数理统计发展简史

数理统计起源于 17 世纪，经过贝叶斯、高斯等统计学家的贡献，逐渐发展为一门成熟的学科。在现代，随着计算机技术的发展，数理统计在人工智能、大数据等领域得到了广泛应用。

6.1.2 数理统计的主要内容

数理统计主要包括描述性统计、参数估计、假设检验、回归分析等内容，用于从数据中提取信息、做出决策和预测。

6.2 总体与样本

6.2.1 总体与样本简介

总体是研究对象的全体，样本是从总体中抽取的一部分个体。统计分析通常基于样本来推断总体特征。

6.2.2 数据的特征

数据的特征包括集中趋势（均值、中位数、众数）和离散程度（方差、标准差、极差）等。

6.2.3 统计量

统计量是样本数据的函数，用于描述样本特征和推断总体参数。常见的统计量有样本均值、样本方差等。

综合案例及应用：计算样本统计量

案例描述 ：计算一组数据的均值、方差和标准差。

import numpy as np
# 数据
data = np.array([12, 15, 18, 22, 25, 30, 35, 45])
# 计算均值
mean = np.mean(data)
print("均值：", mean)
# 计算方差
variance = np.var(data)
print("方差：", variance)
# 计算标准差
std_dev = np.std(data)
print("标准差：", std_dev)

6.3 参数估计

6.3.1 最大似然估计

最大似然估计是通过最大化似然函数来估计总体参数的方法。它假设样本数据独立同分布，并寻找使似然函数最大的参数值。

6.3.2 贝叶斯估计

贝叶斯估计是基于贝叶斯定理，结合先验分布和样本数据来估计参数的后验分布。

6.3.3 点估计与矩估计

点估计是用样本统计量估计总体参数的单个值。矩估计是通过样本矩估计总体矩，从而估计总体参数。

6.3.4 蒙特卡罗方法的基本原理

蒙特卡罗方法是一种通过随机抽样来数值计算的方法。它在统计、物理、金融等领域广泛应用。

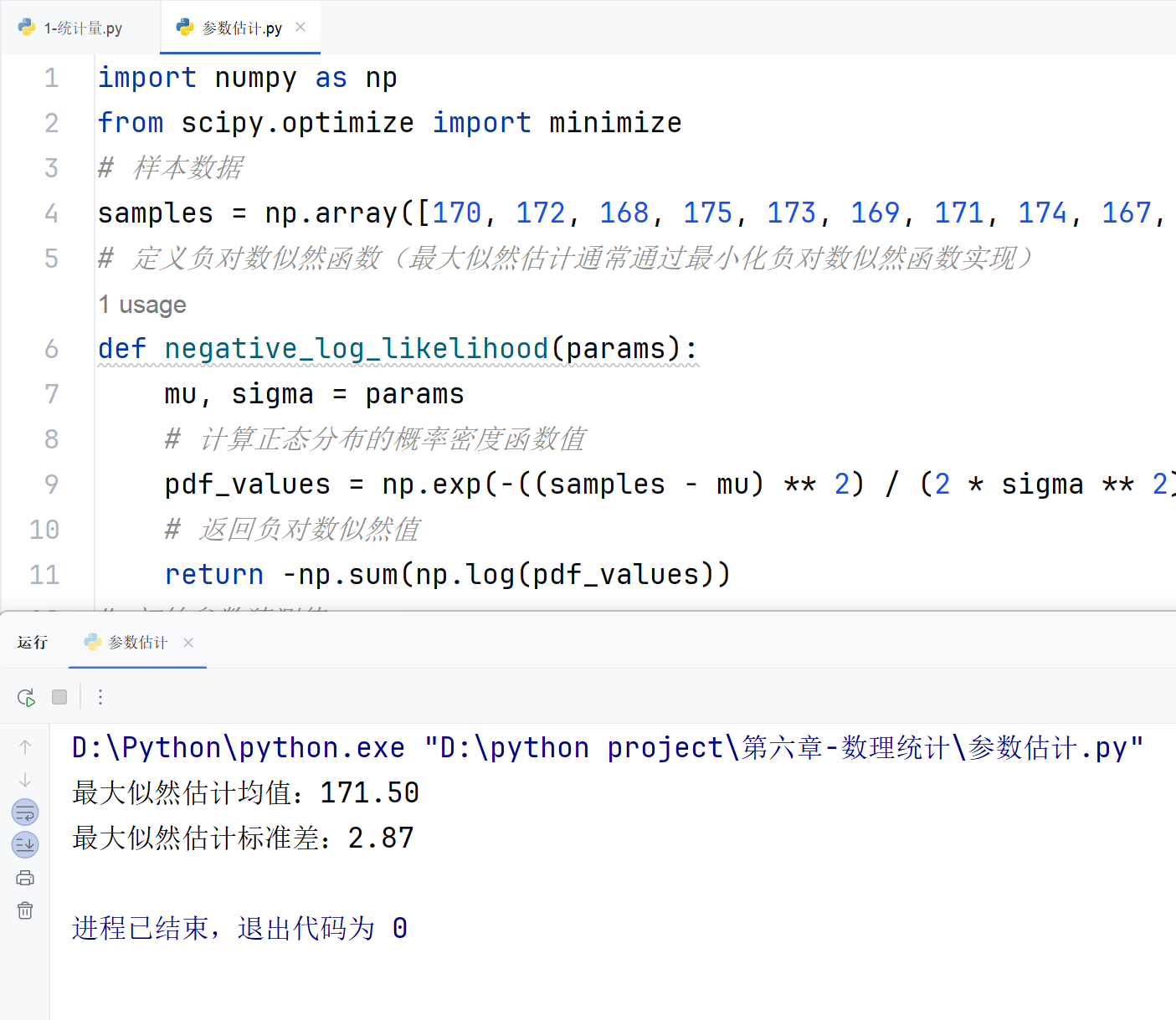
综合案例及应用：最大似然估计

案例描述 ：假设某地男性身高服从正态分布，抽取 10 个样本，估计该正态分布的均值和方差。

import numpy as np
from scipy.optimize import minimize
# 样本数据
samples = np.array([170, 172, 168, 175, 173, 169, 171, 174, 167, 176])
# 定义负对数似然函数（最大似然估计通常通过最小化负对数似然函数实现）
def negative_log_likelihood(params):mu, sigma = params# 计算正态分布的概率密度函数值pdf_values = np.exp(-((samples - mu) ** 2) / (2 * sigma ** 2)) / (sigma * np.sqrt(2 * np.pi))# 返回负对数似然值return -np.sum(np.log(pdf_values))
# 初始参数猜测值
initial_guess = [170, 5]
# 进行最小化优化
result = minimize(negative_log_likelihood, initial_guess, method='BFGS')
# 输出结果
estimated_mu, estimated_sigma = result.x
print(f"最大似然估计均值：{estimated_mu:.2f}")
print(f"最大似然估计标准差：{estimated_sigma:.2f}")

6.4 假设检验

6.4.1 基本概念

假设检验是根据样本数据对总体参数的假设做出接受或拒绝决策的过程。它包括原假设、备择假设、检验统计量和显著性水平等。

6.4.2 Neyman-Pearson 基本引理

Neyman-Pearson 基本引理提供了在给定显著性水平下，构造最有效检验的方法。

6.4.3 参数假设检验

参数假设检验是对总体参数（如均值、方差）进行检验。常见的检验方法有 t 检验、z 检验等。

6.4.4 卡方检验

卡方检验用于检验样本数据与理论分布之间的拟合程度，或检验两个分类变量之间的独立性。

综合案例及应用：单样本 t 检验

案例描述 ：某班级学生某次考试的平均成绩为 75 分，现抽取 20 名学生的成绩，检验该班级平均成绩是否显著高于 70 分（显著性水平为 0.05）。

import numpy as np
from scipy import stats
# 设置样本数据（这里假设了20个样本）
np.random.seed(42)
sample_scores = np.random.normal(loc=75, scale=10, size=20)
# 原假设：班级平均成绩等于70分
# 备择假设：班级平均成绩大于70分（单尾检验）
mu_0 = 70
# 计算t统计量和p值
t_stat, p_value = stats.ttest_1samp(sample_scores, mu_0)
# 因为是单尾检验，所以p值需要调整
p_value_one_tailed = p_value / 2
# 输出结果
print(f"t统计量：{t_stat}")
print(f"单尾检验p值：{p_value_one_tailed}")
# 判断是否拒绝原假设
alpha = 0.05
if p_value_one_tailed < alpha and t_stat > 0:print("拒绝原假设，样本均值显著大于70。")
else:print("不拒绝原假设，样本均值与70没有显著差异。")

6.5 回归分析

6.5.1 一元线性回归

一元线性回归用于研究一个自变量与一个因变量之间的线性关系。通过最小二乘法估计回归系数。

6.5.2 可化为一元线性回归的非线性回归

某些非线性回归可以通过变量变换转化为线性回归问题，如对数变换、倒数变换等。

6.5.3 多元线性回归

多元线性回归研究多个自变量与一个因变量之间的线性关系。通过矩阵运算估计回归系数。

综合案例及应用：一元线性回归

案例描述 ：分析广告投入与销售额之间的关系，建立一元线性回归模型，并预测广告投入为 30 万元时的销售额。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 广告投入和销售额数据
advertising = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]).reshape(-1, 1)
sales = np.array([2, 3, 5, 7, 8, 10, 12, 15, 17, 19])
# 创建线性回归模型并拟合数据
model = LinearRegression()
model.fit(advertising, sales)
# 回归系数和截距
coefficient = model.coef_[0]
intercept = model.intercept_print(f"回归系数（斜率）：{coefficient}")
print(f"截距：{intercept}")
# 预测广告投入为30万元时的销售额
predicted_sales = model.predict(np.array([[30]]))
print(f"广告投入为30万元时的预测销售额：{predicted_sales[0]:.2f}")
# 绘制回归直线
plt.scatter(advertising, sales, color='blue', label='实际数据点')
plt.plot(advertising, model.predict(advertising), color='red', label='回归直线')
plt.xlabel('广告投入（万元）')
plt.ylabel('销售额（万元）')
plt.title('广告投入与销售额的一元线性回归分析')
plt.legend()
plt.grid(True)
plt.show()

6.6 实验：基于 Python 实现用蒙特卡罗方法求圆周率

6.6.1 实验目的

通过蒙特卡罗方法近似计算圆周率 π 的值，理解随机抽样在数值计算中的应用。

6.6.2 实验要求

使用 Python 实现蒙特卡罗方法，模拟随机点在单位正方形和单位圆内的分布，计算 π 的近似值。

6.6.3 实验原理

在单位正方形内随机生成大量点，统计落在单位圆内的点数。根据几何概率，圆内点数与总点数之比近似等于圆面积与正方形面积之比（π/4）。

6.6.4 实验步骤

生成大量随机点（x, y），其中 x 和 y 均在 [0, 1) 范围内。
判断每个点是否落在单位圆内（x² + y² ≤ 1）。
统计圆内点数和总点数。
根据比例计算 π 的近似值。

6.6.5 实验结果

import numpy as np
# 设置随机种子以确保结果可重复
np.random.seed(42)
# 总模拟次数
total_simulations = 1000000
# 生成随机点
x_random = np.random.rand(total_simulations)
y_random = np.random.rand(total_simulations)
# 判断点是否在单位圆内
distances_squared = x_random**2 + y_random**2
points_inside_circle = distances_squared <= 1
# 计算圆周率近似值
pi_estimate = 4 * np.sum(points_inside_circle) / total_simulations
print(f"蒙特卡罗方法估计的圆周率值（{total_simulations}次模拟）：{pi_estimate}")

6.7数理统计总结

概念	定义与说明	常见应用
总体与样本	总体是研究对象的全体，样本是总体的一部分	样本均值、方差，统计推断
参数估计	通过样本估计总体参数的方法	最大似然估计，贝叶斯估计，矩估计
假设检验	根据样本数据检验总体参数的假设	t检验，z检验，卡方检验
回归分析	研究变量间关系的统计方法	一元线性回归，多元线性回归，非线性回归

通过本文的学习，希望大家对数理统计在人工智能中的应用有了更深入的理解。在实际操作中，多进行代码练习，可以更好地掌握这些数学工具，为人工智能的学习和实践打下坚实的基础。资源绑定附上完整资源供读者参考学习！