当前位置：首页 > news >正文

【优选算法 | 前缀和】前缀和算法：高效解决区间求和问题的关键

news 来源：原创 2025/7/7 3:12:19

在这里插入图片描述

算法	相关知识点	可以通过点击	以下链接进行学习	一起加油！
双指针	滑动窗口	二分查找

在本篇文章中，我们将深入解析前缀和算法的原理。从基础概念到实际应用，带你了解如何通过前缀和高效解决数组求和、区间查询等问题。无论你是刚接触算法的新手，还是希望提升代码性能的老手，前缀和都是你提升算法效率的重要利器！

请添加图片描述

Alt

🌈个人主页：是店小二呀
🌈C/C++专栏：C语言\ C++
🌈初/高阶数据结构专栏：初阶数据结构\ 高阶数据结构
🌈Linux专栏： Linux
🌈算法专栏：算法
🌈Mysql专栏:Mysql

🌈你可知:无人扶我青云志我自踏雪至山巅请添加图片描述

文章目录

- DP34.【模板】前缀和
- DP35.【模板】二维前缀和
- 724. 寻找数组的中心下标
- 238. 除自身以外数组的乘积
- 560. 和为 K 的子数组
- 974.和可被 K 整除的子数组
- 525. 连续数组
- 1314. 矩阵区域和

DP34.【模板】前缀和

【题目】：DP34.【模板】前缀和

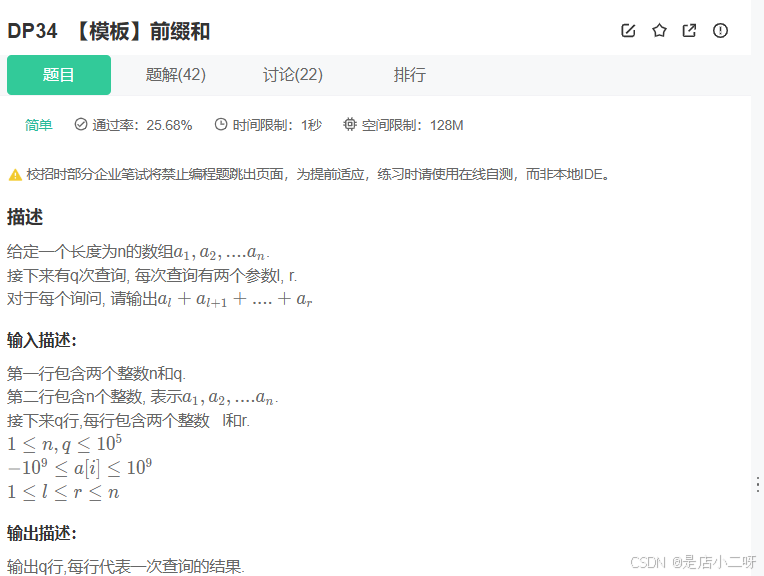
在这里插入图片描述

示例1输入：
3 2
1 2 4
1 2
2 3
输出：
3
6

解法一：暴力解法

在这里插入图片描述

每次询问时，求出该区间的和以及包含多少个q，并计算其重复次数，所消耗时间复杂度O(n*q)

解法二:前缀和

前缀和是用于"快速得到某一段区间的和"，所需要消耗时间复杂度为O(q+n)

第一步：预处理"前缀和数组"

在这里插入图片描述

dp[i]表示:[1, i]区间内所有元素的和
dp[i - 1]表示：[1, i - 1]区间内所有元素的和

通过arr数组和"前缀和数组"之间关系，没有必要重新遍历arr数组求和，再填写到"前缀和数组"内，其中推导出递推公式：dp[i] = dp [i - 1] + add[i]。

预处理前缀和数组的过程，本质上就是个小的动态规划。无非就是状态标识，状态转移方程。

第二步：使用前缀和数组

在这里插入图片描述

使⽤前缀和数组，「快速」求出「某⼀个区间内」所有元素的和：当询问的区间是 [l, r] 时：区间内所有元素的和为： dp[r] - dp[l - 1] 。

默认情况下，C++ 中 vector<int> dp(n + 1) 会将 dp 数组的所有元素初始化为 0，因此 dp[0] 也是 0。

#include <iostream>
#include <vector>
using namespace std;int main() 
{//1.读取数据int n, q;cin >> n >> q;vector<int> arr(n + 1);//输入原始数组for(int i = 1; i <= n; i++) cin >> arr[i];//2.预处理出来一个前缀和数组vector<long long> dp(n + 1);//防止溢出//输入DP数组数据for(int i = 1; i <= n; i++) dp[i] = dp[i - 1] + arr[i];int l = 0, r = 0;while(q--){cin >> l >> r;cout << dp[r] - dp[l - 1] << endl;}return 0;
}

【细节问题】：为什么下标从1开始计数？

在这里插入图片描述

通过[0, 2]和[1,2]分析可得，dp[-1]下标是负数存在越界访问，dp[0]也需要单独赋值。不然下标1开始计算，解决了上面两个问题。

为了处理边界情况
初始化:添加虚拟节点（辅助节点）

在这里插入图片描述

DP35.【模板】二维前缀和

【题目】：DP35.【模板】二维前缀和

在这里插入图片描述

输入：

输出：

8
25
32

【算法思路】

解法一：暴力解法->模拟

在这里插入图片描述

解法二：前缀和

1.预处理出来一个前缀和矩阵

其中，我们需要知道dp[i] [j]元素表达含有，更好地去使用前缀和矩阵解决问题。

dp[i] [j]表示：从[1, 1]位置到[i, j]位置，这段区间里面所有元素的和

不理解为什么是从[1, 1]位置开始，可以结合上一道题目解析和本题数据氛围限制理解。

2.找到状态转移方程

在这里插入图片描述

根据 dp[i][j] 元素的含义，推导其状态转移方程，分析是否存在等价关系，或者从前状态推导出后状态。在推导过程中，要注意细节，特别是从 dp[i-1][j-1] 或者面积的组合角度入手，确保理解 dp[i][j] 的具体含义。

3.使用前缀和矩阵

在这里插入图片描述

细节问题：这里D面积是[x1, y1] -> [x2, y2]，而对于A面积是[1, 1] -> [x1 -1, y1 - 1]，注意看红色的线。

【代码实现】

#include <iostream>
using namespace std;
#include <vector>int main() 
{int n = 0, m = 0, q = 0;cin >> n >> m >> q;//1.读入数据vector<vector<int>> arr(n + 1, vector<int>(m + 1));for(int i = 1; i <= n; i++)for(int j = 1;j <= m; j++)cin >> arr[i][j];//2.处理前缀和矩阵vector<vector<long long>> dp(n + 1,vector<long long>(m + 1));for(int i = 1; i <= n; i++)for(int j = 1;j <= m; j++)dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + arr[i][j] - dp[i- 1][j - 1];//3.使用前缀和矩阵int x1 = 0, y1 =0, x2 = 0, y2 = 0;while(q--){cin >> x1 >> y1 >> x2 >> y2;cout << dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1] <<endl;}return 0;  
}

724. 寻找数组的中心下标

【题目】：724. 寻找数组的中心下标

在这里插入图片描述

【算法思路】

使用前缀和算法时，不能死记硬背模板，关键是理解其思想，并根据具体问题灵活调整。模板中的算法思路可以为我们提供思路，但需要根据题目微调。

对于需要快速统计某个元素之前或之后所有元素和的情况，可以分别构建前缀和矩阵和后缀和矩阵。通过图示帮助分析问题，提升理解与解决效率。

f:前缀和数组:f[i]表示:[0, i - 1]区间，所有元素的和
g:后缀和数组:g[i]表示:[i + 1, n - 1]区间，所有元素的和

【个人思考】:在推导状态转移方程时，首先理解当前定义的含义，并从前后元素的关系入手，逐步构建方程。举个例子，假设 f[i] 表示区间 [0, i-1] 所有元素的和，那么 f[i-1] 表示区间 [0, i-2] 的和。为了使 f[i] 满足其定义，我们需要将 nums[i-1] 加入，从而得到状态转移方程。

【细节问题】：

f(0) = 0，左边没有元素
g(0) = 0，右边没有元素
f:从左向右
g:从右向左
如果出现多个中心下标，[0,0,0,0] 返回最左边位置

【代码实现】：

class Solution {
public:int pivotIndex(vector<int>& nums){int n = nums.size();vector<int> f(n);vector<int> g(n);for(int i = 1; i < n; i++)  f[i] = f[i - 1] + nums[i - 1];for(int i = n - 2; i >= 0; i--)g[i] = g[i + 1] + nums[i + 1];for(int i = 0; i < n; i++) if(f[i] == g[i]) return i;return -1;}
};

从下标 1 到 n-2 开始处理，因为下标 0 和 n-1 对应的数据已经特殊处理为 0，且没有实际意义。如果从下标 0 或 n-1 开始，可能会导致越界访问。

238. 除自身以外数组的乘积

【题目】：238. 除自身以外数组的乘积

在这里插入图片描述

【算法思路】

解法一：暴力解法

直接暴力枚举，从从前往后遍历，枚举每一个位置需要O（n），同时需要遍历每个数组，整体时间复杂度是个N方级别的

解法二：前后缀积

在这里插入图片描述

如果需要用到前后数据元素积，我们需要搭建前缀积矩阵与后缀积矩阵

在这里插入图片描述

“这个题和 ‘724. 寻找数组的中心下标’ 的算法思路非常相似，主要区别在于细节处理，尤其是临界元素的取值问题。根据 f[i] = f[i-1] + nums[i-1] 的规律，当 i = 1 时，必须设定 f[0] = 1，以确保 f[1] 表示区间 [0, 0] 对应的原始数据 nums[0]，因为1乘任何数都等于它本身。

在“除自身以外数组的乘积”的解法中，我们不需要计算每个元素前面和后面的乘积，而是通过前缀积 f[i] 和后缀积 g[i] 来在每个位置 i 计算出左边和右边的乘积，从而避免了除法的使用。

最终每个 output[i] 的值是 f[i] * g[i]，这就得到了除 nums[i] 外的所有元素的乘积。

【代码实现】

class Solution {
public:vector<int> productExceptSelf(vector<int>& nums){int n = nums.size();vector<int> f(n), g(n);f[0] = g[n - 1] = 1;for(int i = 1; i < n; i++) f[i] = f[i - 1] * nums[i - 1];for(int i = n - 2; i >= 0; i--) g[i] = g[i + 1] * nums[i + 1];vector<int> ret(n);for(int i = 0; i < n; i++) ret[i] = f[i] * g[i];return ret;}
};

560. 和为 K 的子数组

【题目】：560. 和为 K 的子数组

在这里插入图片描述

【算法思路】

解法一：暴力枚举

如果使用暴力枚举可以解决这道问题，但是我们可以有更好的解法

解法二：前缀和 + 哈希表

返回和为 k 的子数组个数”这类问题，我们可以通过前缀和 + 哈希表来优化。一个关键的思路是“以 i 位置为结尾的所有子数组”。

实际上，问题本质上仍然是暴力枚举的思路，之前我们是“以 i 位置为开始的所有子数组”。之所以选择“以 i 位置为结尾的子数组”，是因为我们想使用“前缀和 + 哈希表”来快速求出子数组的和。通过这种方式，我们能够高效地统计子数组的次数。

如果使用“以 i 位置为开始的子数组”，我们需要从已知位置向未知位置查找，不容易统计之前出现的子数组。而“以 i 位置为结尾的子数组”则是从未知位置向已知位置查找，可以通过哈希表来快速得出子数组和，提升效率。

问题转化为前缀和，就是之前前缀和数据可以重复使用，多转一。

在这里插入图片描述

【魔鬼细节问题】

1.【sum[i] - k含义】

对于某个 i 位置，考虑到子数组和为 k 的问题，可以通过等价关系转化为：找出多少个前缀和等于 sum[i] - k。这里的 sum[i] - k 不是固定值，而是动态计算得到的。通过不断更新的前缀和，我们可以找到符合条件的子数组数量，判断以 i 位置为结尾的子数组和是否等于 k。

2.【前缀和加入哈希表时机】

在计算第i个位置之前，哈希表仅保存位置[0, i-1]的前缀和。如果提前将元素加入前缀和，效果不如直接暴力枚举，且会导致哈希表统计位置时出现问题。

3.【不用真的创建一个前缀和数组】

dp[i] = dp[i - 1] + nums[i]，这里无需额外创建前缀和数组来存储数据，哈希表负责处理前缀和。通过遍历一次前缀和并建立哈希表的映射关系即可。

4.【默认前缀和全部等于k】

哈希表在后续统计时，如果 count(x) == 0，可能导致无法正确统计。因此，单独设置 hash[0] = 1 是为了避免这种情况。没有 hash[0] = 1 时，程序会缺少一个初始的前缀和 0。假设某个子数组的和恰好等于 k，且该子数组从数组的开头开始，如果没有这个初始前缀和 0，就无法通过 hash[sum - k] 条件识别这个子数组。

【代码实现】

class Solution {
public:int subarraySum(vector<int>& nums, int k) {unordered_map<int, int> hash;int sum = 0, ret =0;hash[0] = 1; //确保第一个数for(auto x : nums){sum += x;if(hash.count(sum - k)) ret += hash[sum - k];hash[sum]++;}return ret;}
};

974.和可被 K 整除的子数组

【题目】：974. 和可被 K 整除的子数组

在这里插入图片描述

【算法思路】

本题算法数量同"560. 和为 K 的子数组"类似，重点在于细节处理上。

【补充知识】:同余定理

在这里插入图片描述

这里只需要记住结论:(a - b) / p = k ....0 -> a% p = b% p

C++,Java：[负数% 正数]的结果以及修正

在这里插入图片描述

本题思路：

在这里插入图片描述

找到在 [0, i - 1] 区间内，有多少前缀和的余数(x% k)等于 sum[i] % k 的即可

【细节问题】

1.修正后的余数:int r = (sum % k + k) % k;

2.填入哈希表时机

3.0余数处理:hash[0 % k] = 1; // 0 这个数的余数

4.不用真的创建一个前缀和数组

【代码实现】

class Solution {
public:int subarraysDivByK(vector<int>& nums, int k) {unordered_map<int, int> hash;hash[0 % k]++;int sum = 0, ret = 0;for(auto x : nums){sum += x;int r = (sum % k + k) % k;if(hash.count(r)) ret += hash[r];hash[r]++;}return ret;}
};

525. 连续数组

【题目】：525. 连续数组

在这里插入图片描述

【算法思路】

本题要求找出一个连续子数组，使得其中 0 和 1 的数量相等。

如果将 0 记为 -1，1 记为 1，问题就转化为寻找一个和为 0 的子数组。
这个思路和 LeetCode 560 题“和为 K 的子数组”是一样的。

【细节问题】

1.【默认前缀和为0的情况】

当前缀和为 0 时，如果不做处理，无法正确计算子数组的长度。之所以设置 hash[0] = -1，是因为在计算子数组长度时，i - j 代表的是当前位置和前一个位置的差。为了能够正确计算从数组起始位置到当前下标的子数组长度，我们默认前缀和为 0 时的下标是 -1。

2.【哈希表存储】

hash<int_前缀和，int _下标>

3.如果有重复<sum, i>

在这里插入图片描述

只保留前面那一对<sum, i>

4.计算长度

在这里插入图片描述

【代码实现】

class Solution {
public:int findMaxLength(vector<int>& nums) {unordered_map <int, int> hash;hash[0] = -1; // 默认有⼀个前缀和为 0 的情况int sum = 0, ret = 0;for(int i = 0; i < nums.size();i++){sum += nums[i] == 0 ? -1 : 1;if(hash.count(sum)) ret = max(ret,i - hash[sum]);else hash[sum] = i;}return ret;}
};

1314. 矩阵区域和

【题目】：1314. 矩阵区域和

在这里插入图片描述

【算法思路】

该题目中需要计算"矩阵前缀和"，需要结合"【模板】二维前缀和"里面关于矩阵前缀和计算和使用。

通过

以下是模板，不用死记硬背，画图可以很快推理出来

在这里插入图片描述

计算矩阵前缀和:dp[i][j] = dp[i][j-1] + dp[i-1][j] - dp[i-1][j-1] + mat[i - 1][j - 1];

使用部分矩阵前缀和：answer[i][j] = dp[x2][y2] - dp[x2][y1 -1] - dp[x1 - 1][y2] + dp[x1 - 1][y1 - 1];

【细节问题】

1.【通过k长度计算范围前缀和】

在这里插入图片描述

2.【mat矩阵同dp表下标映射关系】

在这里插入图片描述

这里主要体现为 mat[i][j] 映射到 mat[i - 1][j - 1]，由于 dp 表的索引是从 1 开始，因此 x1、x2、y1、y2 都需要加 1 来适配原始矩阵的 0-based 索引。

class Solution {
public:vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {int m = mat.size(), n = mat[0].size();//创建dp表vector<vector<int>> dp(m + 1, vector<int>(n + 1));//填充dp表数据for(int i = 1; i <= m; i++)for(int j = 1; j <= n; j++)dp[i][j] = dp[i][j-1] + dp[i-1][j] - dp[i-1][j-1] + mat[i - 1][j - 1];//mat[i - 1][j - 1],映射mat表格下标int x1 = 0, y1 = 0, x2 = 0, y2 = 0;//使用dp表填充新表格进行返回vector<vector<int>> answer(m, vector<int>(n));for(int i = 0; i < m; i++)for(int j = 0; j < n; j++){x1 = max(i - k, 0) + 1;y1 = max(j - k, 0) + 1;x2 = min(i + k, m - 1)+ 1;y2 = min(j + k, n - 1) + 1;answer[i][j] = dp[x2][y2] - dp[x2][y1 -1] - dp[x1 - 1][y2] + dp[x1 - 1][y1 - 1];}return answer;}
};

在这里插入图片描述
快和小二一起踏上精彩的算法之旅！关注我，我们将一起破解算法奥秘，探索更多实用且有趣的知识，开启属于你的编程冒险！

文章目录

DP34.【模板】前缀和

DP35.【模板】二维前缀和

724. 寻找数组的中心下标

238. 除自身以外数组的乘积

560. 和为 K 的子数组

974.和可被 K 整除的子数组

525. 连续数组

1314. 矩阵区域和

相关文章：