当前位置：首页 > news >正文

6.7.图的深度优先遍历(英文缩写DFS)

news 来源：原创 2025/8/15 19:58:38

树是特殊的图，没有回路的图就是树
BFS与DFS的区别在于，BFS使用了队列，DFS使用了栈

一.深度优先遍历：

1.树的深度优先遍历：

树的深度优先遍历分为先根遍历和后根遍历。

以树的先根遍历为例：

上述图片里树的先根遍历序列为1、2、5、6、3、4、7、8
树的先根遍历中新找到的相邻结点一定是没有被访问过的

2.图的深度优先遍历：

visited数组用来记录图中的顶点是否被访问过，MAX_VERTEX_NUM是图中顶点的最大个数，DFS函数的形参Graph G和int v分别表示图和图的顶点编号，visit函数用于访问顶点，visit(v)表示访问第v号顶点，visited[v]=true表示第v号顶点被访问过
DFS函数中的for循环，其中FirstNeighbor(G,v)用来找第v号顶点在G中的第一个邻接点，若存在该邻接点，返回该第一个邻接点的编号，赋值给w，如果w非负，执行for循环，首先判断是否执行if语句，若符合条件!visited[w]为true即第w号顶点没有被访问过，那么就执行if语句，调用DFS函数，该层for循环结束，再执行NextNeighbor(G,v,w)函数，第w号顶点是第v号顶点的第一个邻接点，找除了第w号顶点外第v号顶点的的下一个邻接点，找到了返回该邻接点的顶点号，赋值给w，判断是否非负，若非负，继续执行for循环，如不是非负即小于0，跳出for循环
图的深度优先遍历类似树的先根遍历，都是先访问完一个结点，然后再用一个循环依次检查和这个结点相邻的其他结点，然后进行更深一层的访问，只不过对于图的深度优先遍历，增加了一个数组用来标记顶点是否被访问过
对于图而言，通过某一个顶点找到的与之相邻的其他顶点有可能是已经被访问过的，所以可以设置一个数组，用来标记每一个顶点是否被访问过

3.模拟图的深度优先遍历的执行过程：

如下图，以上述图片的图为例，假设从2号顶点出发深度优先遍历该图，所以第一次调用DFS函数的时候，传入的v的值为2，然后调用visit函数访问2号顶点，修改2号顶点对应的visited的值为true，表示2号顶点已经被访问过，for循环用来检查和2号顶点相邻的其他顶点，和2号顶点相邻的顶点是1、6号顶点，其中和2号顶点相邻的第一个顶点是1号顶点，此时1号顶点没有被访问过：

如下图，因此第二次调用DFS函数时传入的参数为1，然后调用visit函数访问1号顶点，修改1号顶点对应的visited的值为true，表示1号顶点已经被访问过，for循环用来检查和1号顶点相邻的其他顶点，和1号顶点相邻的顶点是2、5号顶点，其中和1号顶点相邻的第一个顶点是2号顶点，由于2号顶点对应的visited的值为true即已经被访问过，因此2号顶点会被跳过，通过for循环找到下一个和1号顶点相邻接的顶点是5号顶点：

如下图，因此第三次调用DFS函数时传入的参数为5，然后调用visit函数访问5号顶点，修改5号顶点对应的visited的值为true，表示5号顶点已经被访问过，for循环用来检查和5号顶点相邻的其他顶点，和5号顶点相邻的顶点是1号顶点，由于1号顶点对应的visited的值为true即已经被访问过，因此1号顶点会被跳过，此时和5号顶点相邻的所有顶点全部访问完毕，意味着5号顶点对应的for循环什么都不会做：

如下图，所以5号顶点对应的DFS函数执行完毕，之后就会返回上一层的递归调用，即1号顶点这一层：

如下图，由于之前处理的5号顶点已经是1号顶点的最后一个邻接点，所以1号顶点的for循环执行完毕，因此1号顶点对应的DFS函数执行结束，最终返回上一层的递归调用，即2号顶点这一层：

如下图，此时2号顶点的第一个邻接点即1号顶点已经被处理完，通过NextNeighor(G,v,w)函数找到除了1号顶点之外后一个和2号顶点相邻接的顶点即6号顶点，6号顶点此时还没有被访问过：

如下图，因此接下来调用DFS函数时传入的参数为6，然后调用visit函数访问6号顶点，修改6号顶点对应的visited的值为true，表示6号顶点已经被访问过，for循环用来检查和6号顶点相邻的其他顶点，和6号顶点相邻的顶点是2、3、7号顶点，由visited数组可知2号顶点已经被访问过，因此会跳过2号顶点，开始访问3号顶点：

如下图，因此接下来调用DFS函数时传入的参数为3，然后调用visit函数访问3号顶点，修改3号顶点对应的visited的值为true，表示3号顶点已经被访问过，for循环用来检查和3号顶点相邻的其他顶点，和3号顶点相邻的顶点是4、6、7号顶点，第一个被访问的顶点是4号顶点，由visited数组可知4号顶点还没有被访问过：

如下图，因此接下来调用DFS函数时传入的参数为4，然后调用visit函数访问4号顶点，修改4号顶点对应的visited的值为true，表示4号顶点已经被访问过，for循环用来检查和4号顶点相邻的其他顶点，和4号顶点相邻的顶点是3、7、8号顶点，第一个被访问的顶点是3号顶点，由visited数组可知3号顶点已经被访问过，因此会跳过3号顶点，开始访问7号顶点：

如下图，因此接下来调用DFS函数时传入的参数为7，然后调用visit函数访问7号顶点，修改7号顶点对应的visited的值为true，表示7号顶点已经被访问过，for循环用来检查和7号顶点相邻的其他顶点，和7号顶点相邻的顶点是3、4、6、8号顶点，由visited数组可知，和7号顶点相邻接的顶点中，只有8号顶点还没有被访问过，因此开始访问8号顶点：

如下图，因此接下来调用DFS函数时传入的参数为8，然后调用visit函数访问8号顶点，修改8号顶点对应的visited的值为true，表示8号顶点已经被访问过，for循环用来检查和8号顶点相邻的其他顶点，和8号顶点相邻的顶点是4、7号顶点，由visited数组可知，4、7号顶点都已经被访问过，所以8号顶点的DFS函数执行完毕：

如下图，返回上一层即7号顶点这一层，此时和7号顶点相邻的所有顶点都已经全部被访问完毕，所以继续返回上一层：

如下图，返回到4号顶点这一层，此时和4号顶点相邻的所有顶点都已经全部被访问完毕，所以继续返回上一层：

如下图，其他的类似，最终函数调用栈清空，上述图片的图遍历完毕：

如上图，最终得出从2号顶点出发，进行上述图的深度优先遍历，得到的深度遍历序列为2，1，5，6，3，4，7，8。

4.图的深度优先遍历算法存在的问题与优化：

上述图片的代码存在一个问题，就是如果遍历的图是非连通图，则无法遍历完所有顶点，如下图所示：

例如从2号顶点出发进行深度优先遍历上述图片里的图，调用DFS函数，可以遍历完1、2、3、4、5、6、7、8号顶点，但9、10、11号顶点无法遍历到，解决方案如下：

DFSTraverse函数的形参Graph G表示图；vexnum表示图中顶点的个数，G.vexnum表示图中顶点的个数，v是顶点编号
DFSTraverse函数的第一个for循环用来把visited数组全部赋值为false，表示图中所有顶点都没有被访问过
DFSTraverse函数的第二个for循环用来检查是否有顶点还没有被访问过，如果有，visited[v]的值为false，!visited[v]的值为true，就会执行if语句再次调用DFS函数把未访完的顶点访问完毕
注：DFSTraverse函数的第二个for循环必须从第一个顶点出发开始遍历，如果从中间的顶点出发开始遍历，就会使得前面的顶点无法遍历到->如上图，必须从1号顶点出发，由于是非连通图，只能把1、2、3、4、5、6、7、8号顶点访问完，此时发现第9号顶点对应visited的值为false，意味着9号顶点还没有被访问，因此从9号顶点出发，再次调用DFS函数访问剩下的顶点，通过9号顶点就可以把9、10、11号顶点全部访问完，最终上述图片的图深度优先遍历完毕

二.图的深度优先遍历算法的空间复杂度：

如上图，图的深度优先遍历算法的空间复杂度主要取决于DFS函数的递归调用。

1.最坏的情况：

如上图，比如从1号顶点出发开始深度优先遍历图，那么DFS函数递归调用栈的深度就会与图中的顶点个数相等（因为1号顶点与2、3、4、5、6、7、8号顶点都邻接，意味着函数递归调用栈会把图中8个顶点即所有顶点都入栈），假设图中有V个顶点，因此最坏的情况为O( |V| )->之所以这个是最坏情况，是因为递归深度达到了最大值。

2.最好的情况：

如上图，比如从1号顶点出发开始深度优先遍历图，显然在这种情况下DFS函数递归调用栈最多只会有两层（一层是当前访问的顶点，一层是与该顶点相邻接的顶点，不存在第二个与该顶点相邻接的顶点），也就是说只需要常数级即O(1)的空间复杂度。（注：访问顶点时函数递归调用栈最少会有一层，这一层是当前访问的顶点，该顶点不存在邻接点，顶点全部访问完毕时或者不访问顶点时函数递归调用栈为0层）

3.注意：做题时，题目问图的深度优先遍历算法的空间复杂度，没有特别说明的情况下，要答O( |V| )即最坏的情况。

三.图的深度优先遍历算法的时间复杂度：

核心：无论是BFS还是DFS，计算时间复杂度都可以简化为计算访问各个顶点所需要的时间加探索各条边/弧所需要的时间

1.如果图采用邻接矩阵存储：

假设图中有V个顶点，访问|V|个顶点就需要O( |V| )的时间，因为需要遍历，

探索和某一个顶点相邻的边只需要遍历该顶点对应的一整行（或一整列，因为此时是无向图，无向图的邻接矩阵是对称的）的数据即可，所以查找每个顶点的邻接点即邻接的边需要O( |V| )的时间，

由于总共有|V|个顶点，所以整体来看时间复杂度就是O( |V| * |V| )。

2.如果图采用邻接表存储：

假设图中有V个顶点，访问|V|个顶点就需要O( |V| )的时间，因为需要遍历，

假设图中有E条边，查找某个顶点的邻接点即邻接的边共需要O( |E| )的时间，因为查找某个顶点的邻接点即邻接的边只需要遍历该顶点对应的链表即可，链表可能包含所有的边，所以共需要O( |E| )的时间，

由于需要先查找所要操作的顶点，再找邻接的边，所以时间复杂度为O( |V|+|E| )。

四.深度优先遍历序列：从哪一个顶点开始遍历（入栈），遍历结束时就是哪个顶点最后一个出栈（先进后出）

假设图使用了邻接矩阵或者邻接表存储，

如上图，邻接表中各个链表中顶点号都是从左向右递增的，因此，对于某一个顶点，要找到与该顶点相邻的其他顶点，在该邻接表中找到的顺序与左边的邻接矩阵找到的顺序是一致的，因为邻接矩阵的顶点号也是从左向右递增的。

1.从2号顶点出发进行深度优先遍历整个图：

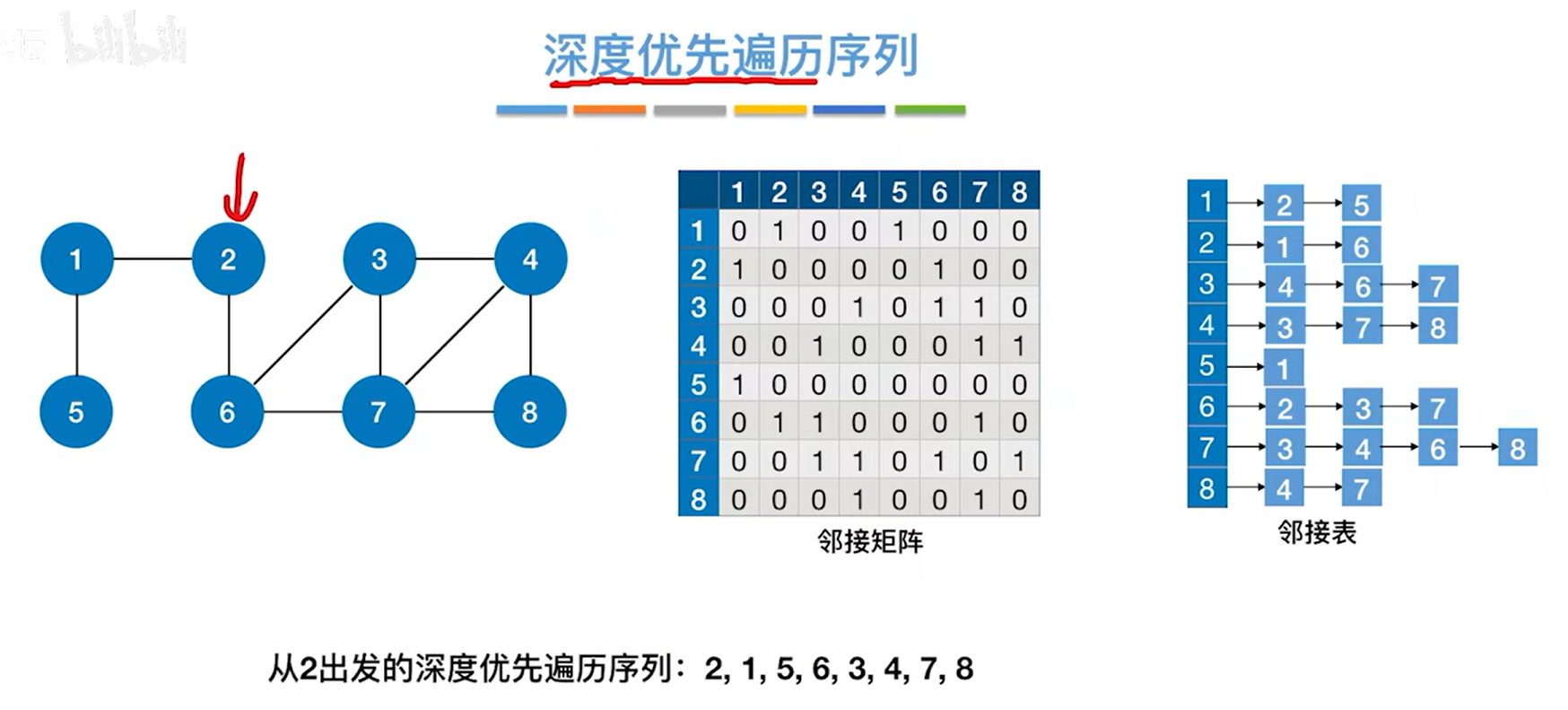
在邻接矩阵和邻接表这两种情况下，如果从2号顶点出发进行深度优先遍历整个图，得到的遍历序列都是2，1，5，6，3，4，7，8（因为此时邻接矩阵和邻接表存储顶点的编号都是递增的）。

2.从3号顶点出发进行深度优先遍历整个图：（详细遍历过程）

如下图，假设图使用邻接表存储：

如上图，第一个访问3号顶点，和3号顶点相邻的第一个顶点是4号顶点（这个直接看3号顶点对应的链表即可知道3号顶点与哪些顶点邻接，其他同理），因此

如上图，第二个访问4号顶点，根据DFS的规则，此时要从4号顶点出发找其他和4号顶点相邻且没有被访问的顶点，与4号顶点相邻的第一个顶点即3号顶点已经被访问过了，因此跳过3号顶点，与4号顶点相邻的第二个顶点即7号顶点没有被访问过，因此

如上图，第三个访问7号顶点，与7号顶点相邻的第一个顶点即3号顶点已经被访问过了，因此跳过3号顶点，与7号顶点相邻的第二个顶点即4号顶点也已经被访问过了，因此跳过4号顶点，与7号顶点相邻的第三个顶点即6号顶点没有被访问过，因此

如上图，第四个访问6号顶点，与6号顶点相邻的第一个顶点即2号顶点没有被访问过，因此

如上图，第五个访问2号顶点，与2号顶点相邻的第一个顶点即1号顶点没有被访问过，因此

如上图，第六个访问1号顶点，与1号顶点相邻的第一个顶点即2号顶点已经被访问过了，因此跳过2号顶点，与1号顶点相邻的第二个顶点即5号顶点没有被访问过，因此

如上图，第七个访问5号顶点，与5号顶点相邻的第一个顶点即1号顶点已经被访问过了，因此跳过1号顶点->此时5号顶点对应的这一层DFS结束，退回到上一层即1号顶点对应的这一层DFS：

如上图，此时与1号顶点相邻的2、5号顶点全部被访问过，因此1号顶点对应的这一层DFS结束，退回到上一层即2号顶点对应的这一层DFS：

如上图，2号顶点对应的这一层DFS还有6号顶点没有检查过，但6号顶点已经访问过了，所以退回到上一层即6号顶点对应的这一层DFS：

如上图，和6号顶点相邻的顶点中还剩3、7号顶点没有检查，但3、7号顶点已经被访问过了，因此退回到上一层即7号顶点对应的这一层DFS：

如上图，和7号顶点相邻的顶点中还剩下8号顶点没有被访问过：

如下图，所以第八个访问8号顶点，

如上图，与8号顶点相邻的顶点中4、7号顶点全部被访问过，所以退回到上一层即7号顶点对应的这一层DFS，

此时7号顶点对应的这一层DFS结束，退回到上一层即4号顶点对应的这一层DFS，

和4号顶点相邻的顶点中还剩8号顶点没有检查，但8号顶点已经被访问过了，因此退回到上一层即3号顶点对应的这一层DFS，

此时还剩下6、7号顶点没有检查，但6、7号顶点已经被访问了，因此退出3号顶点对应的这一层DFS，

最终该图的深度优先遍历结束，得到的遍历序列为3、4、7、6、2、1、5、8：

3.从1号顶点出发进行深度优先遍历整个图：

4.细节：当图使用邻接表存储的话，由于邻接表的表现方式不唯一即顶点对应的链表中顶点号顺序不固定，因此如果从某一个顶点出发深度优先遍历得到的图的序列也可能不一样

对于图而言，它的邻接矩阵存储的表示方式是唯一的，但邻接表的表示方式不唯一，

所以如果图使用邻接表存储的话，从某一顶点出发深度优先遍历图，最终得到的遍历序列也可能不同，这个与BFS一样。

如上图，图使用上述图片呈现的邻接表存储，从2号顶点出发，得到的深度优先遍历序列为2、1、5、6、3、4、7、8，

如下图，此时把邻接表的内容稍作修改即把顶点对应的链表中的顶点号换一下顺序：

从2号顶点出发开始深度优先遍历图，

第一个访问2号顶点，与2号顶点相邻的第一个顶点即6号顶点没有被访问过（这个直接看顶点对应的链表即可）

第二个访问6号顶点，与6号顶点相邻的第一个顶点即2号顶点已经被访问过，因此跳过2号顶点，与6号顶点相邻的第二个顶点即7号顶点还没有被访问过，

第三个访问7号顶点，与7号顶点相邻的第一个顶点即6号顶点已经被访问过，因此跳过6号顶点，与7号顶点相邻的第二个顶点即8号顶点还没有被访问过，

第四个访问8号顶点，与8号顶点相邻的第一个顶点即4号顶点还没有被访问过，

第五个访问4号顶点，与4号顶点相邻的第一个顶点即3号顶点还没有被访问过，

第六个访问3号顶点，与3号顶点相邻的顶点有6、7、4号顶点，这些顶点都被访问过，

因此3号顶点对应的DFS递归调用结束，

返回到4号顶点对应的DFS，与4号顶点相邻的只剩下8、7号顶点没有检查过，但8、7号顶点都被访问过，

所以继续返回到8号顶点对应的DFS，与8号顶点相邻的7号顶点也已经被访问过，

所以继续返回到7号顶点对应的DFS，与7号顶点相邻的3、4号顶点也已经被访问过，

所以继续返回到6号顶点对应的DFS，与6号顶点相邻的3号顶点也已经被访问过，

所以继续返回到2号顶点对应的DFS，与2号顶点相邻的还剩一个1号顶点，1号顶点还没有被访问过，

第七个访问1号顶点，与1号顶点相邻的第一个顶点即2号顶点已经被访问过，因此跳过2号顶点，与1号顶点相邻的第二个顶点即5号顶点还没有被访问过，

第八个访问5号顶点，与5号顶点相邻的第一个顶点即1号顶点已经被访问过，此时5号顶点访问结束，

返回到1号顶点对应的DFS，与1号顶点相邻的所有顶点全部访问完毕，

所以继续返回到2号顶点对应的DFS，此时与2号顶点相邻的顶点全部访问完毕，

最终该图的深度优先遍历结束，得到的遍历序列为2、6、7、8、4、3、1、5：

5.总结：关于图采用邻接表存储

五.深度优先生成树：

下图的两个例子都是从2号顶点开始深度优先遍历图，左边的例子基于之前第一个邻接表，右边的例子基于之前第二个邻接表，由于邻接表的不同，即使从同一个顶点开始深度优先遍历，得到的遍历序列也可能不同，：

深度优先遍历的过程中也是在探索各条边所连接的顶点的过程，

如果通过某一条边找到某个顶点且该顶点还没有被访问过，此时就把这条边标红，通过某一条边找到某个顶点且该顶点被访问过则边标黑，

如果只保留红色的边，把黑色的边去掉，最终的图就变成了一个没有环的树，

如果采用邻接表存储的图，即便从同一个顶点出发进行深度优先遍历，也有可能得到不一样的深度优先遍历序列，因此也会对应不一样的深度优先生成树：

六.深度优先生成森林：

如上图，如果图是非连通的，也就是说要调用多次DFS函数才能把图深度优先遍历完，每调用一次DFS函数，就会生成一棵深度优先生成树，由于上述图片的无向图有两个连通分量，所以需要调用两次DFS函数，因此也会对应的生成两棵深度优先生成树：

上述图片的两棵深度优先生成树就组成了深度优先生成森林。

七.图的遍历与图的连通性：

1.无向图：

对于无向图而言，进行BFS或者DFS时，遍历图中调用BFS函数或者DFS函数的次数等于连通分量数。

如上图，把上述图片的图进行BFS或者DFS时，由于该图有3个连通分量数，因此需要调用3次BFS或者DFS才能遍历完图。

如果无向图是连通图即只有1个连通分量，所以只需要调用1次BFS或者DFS函数即可遍历完图。

2.有向图：

比如从7号顶点出发进行BFS或者DFS，只需要调用一次BFS函数或者DFS函数即可遍历完图，其中一条遍历序列为7、8、4、3、6、2、1、5；

比如从2号顶点出发进行BFS或者DFS，此时只能找到1、5号顶点（因为方向），所以无法调用一次BFS函数或者DFS函数就遍历完图。

特殊情况：有向图是强连通图（也就是从任何一个顶点开始都能找到到达其他所有顶点的路径）

八.总结：

6.7.图的深度优先遍历(英文缩写DFS)

树是特殊的图，没有回路的图就是树 BFS与DFS的区别在于，BFS使用了队列，DFS使用了栈一.深度优先遍历： 1.树的深度优先遍历： 树的深度优先遍历分为先根遍历和后根遍历。以树的先根遍历为例： 上述图片里…...

编程日记 2025/8/15 19:58:38

若依同步企业微信架构及ACTIVITI

企业微信配置 1.进入企业微信后台管理应用管理，新建应用 2.配置网页授权及JS-SDK 将验证文件下载到项目的pubilc下启动项目 npm run dev 然后验证域名归属 3.配置企业可信IP 公网IP地址即可，仅此IP的服务可调用企业微信接口信息 4.构造域名回调域&a…...

编程日记 2025/8/15 7:54:35

PyTorch分布式训练调试方法(跟踪调用过程)

PyTorch分布式训练调试方法(跟踪调用过程) 背景在分布式深度学习训练场景中，通信操作（如AllReduce、Send/Recv）和CUDA操作的时序问题往往难以调试。本工具通过以下方式提供调试支持：拦截所有PyTorch张量操作并记录调用栈监控分布式通信操作的完整生命周期自动生成带时间…...

编程日记 2025/8/14 1:26:20

跟我学C++中级篇——内存异常的分析

一、内存问题引发的现象在实际使用电脑过程中，经常会遇到电脑卡住了，鼠标和键盘也没反应。这时候儿会怎么办？其实此时打开任务管理器，就可以发现，有几种情况：一是CPU占用过高；二是IO占用过高&…...

编程日记 2025/8/16 0:01:24

HTML新标签与核心 API 实战

HTML5 新标签与核心 API 实战引言今天咱们来看看HTML5 新标签以及一些核心 API。 HTML5 的引入彻底改变了 Web 前端开发格局，尤其是其新增的多媒体和交互能力标签。对于前端开发者而言，理解并掌握 <video>、<audio>、<canvas> 和…...

编程日记 2025/8/15 2:00:37

vscode 红色波浪线问题

VSCode 红色波浪线问题终极解决方案问题描述在编写 C 项目时，CMake 编译通过但代码出现红色波浪线，常见问题： #include 提示找不到头文件枚举或类型名未定义成员函数或变量无法识别这些是 VSCode 的 IntelliSense 配置问题&#xff0c…...

编程日记 2025/8/15 23:54:24

类型补充，scan 和数据库管理命令

Redis 数据类型 stream stream 就是一个队列（阻塞队列） Redis 作为一个消息队列的重要支撑，属于是 list 中 blpop 和 brpop 的升级版本 geospatial 主要用于存储地理位置信息，并对存储的信息进行操作存储一些点后&#xff0c…...

编程日记 2025/8/13 15:27:22

AI Agent系列(十) -Data Agent（数据分析智能体）开源资源汇总

AI Agent系列【十】前言一、 Open Interpreter1.1 Open Interpreter的特点1.2 Open Interpreter的优势1.3 Open Interpreter的应用场景二、DB-GPT2.1 核心能力2.2关键特性:2.3 系统架构三、DeepBI3.1 特点前言 DataAgent的能力本质上比较依赖大模型的自然语言转API/SQL/代…...

编程日记 2025/8/15 10:02:25

Vue3 + TypeScript中provide和inject的用法示例

基础写法（类型安全） typescript // parent.component.vue import { provide, ref } from vue import type { InjectionKey } from vue// 1. 定义类型化的 InjectionKey const COUNTER_KEY Symbol() as InjectionKey<number> const USER_KEY Sy…...

编程日记 2025/8/15 12:01:03

【国家能源集团生态协作平台-注册/登录安全分析报告】

前言由于网站注册入口容易被黑客攻击，存在如下安全问题： 暴力破解密码，造成用户信息泄露短信盗刷的安全问题，影响业务及导致用户投诉带来经济损失，尤其是后付费客户，风险巨大，造成亏损无底洞…...

编程日记 2025/8/15 13:37:03

不确定与非单调推理的基本概念

前文我们讨论了建立在经典逻辑基础上的确定性推理，这是一种运用确定性知识进行的精确推理。同时，它又是一种单调性推理，即随着新知识的加人，推出的结论或证明了的命题将单调地增加。但是，人们通常是在信息不完善、不精确的情况下运用不确定性知识进行思维、求解问题的，推…...

编程日记 2025/8/15 23:56:41

系统架构设计师：计算机组成与体系结构（如CPU、存储系统、I/O系统）高效记忆要点、知识体系、考点详解、、练习题并提供答案与解析

计算机组成与体系结构高效记忆要点从CPU、存储系统、I/O系统三大模块展开，结合高频考点与记忆技巧，有助于系统化掌握核心知识点。一、CPU结构与工作原理 1. CPU的组成核心组件： 运算器（ALU） ：负责算术…...

编程日记 2025/8/15 23:54:22

FreeSWITCH中SIP网关（Gateway）操作

freeswitch是一款简单好用的VOIP开源软交换平台。以下是一篇关于FreeSWITCH中SIP网关（Gateway）操作的技术指南，基于提供的官方文档内容整理： 一、网关生命周期管理 1. 创建新SIP Profile并启动 FreeSWITCH支持多SIP Profile&…...

编程日记 2025/8/16 0:01:53

构建自动翻译工作流：技术与实践

一、引言制药行业客户迫切需要一种翻译解决方案，以解决公司内部多样化的翻译难题。他们需要的不仅是提升翻译效率和准确性的工具，更希望能够保持文档的原始格式。我们观察到客户的需求广泛，包括多语言办公文件、研究文档和药品报批文件等&a…...

编程日记 2025/8/15 23:59:33

在pycharm中搭建yolo11分类检测系统--PyQt5学习（二）

第二部分测试本地pycharm通过程序连接远程服务器autodl 模型的推理需要借助远程服务器autodl，但是界面的运行是在pycharm中，我的设想是按钮调用一个py文件就好了。 1. 本地运行PyQt5界面。 2. 当需要载入权重时，通过SSH连接到AutodL服务…...

编程日记 2025/8/15 23:56:12

汽车行驶工况特征参数：从“速度曲线”到“驾驶DNA”的硬核解码

作为新能源汽车行业的从业者，你是否曾困惑于这些问题： 为什么同一款电动车，不同用户的实际续航差异高达30%？如何精准量化驾驶行为对电池寿命的影响？车企标定的“NEDC续航”与真实路况差距的根源是什么？ 这…...

编程日记 2025/8/16 0:01:52

dify本地部署，docker-plugin_daemon-1启动不了,一直报错

解决办法，修改这两个配置，然后重启进入源代码目录，docker文件夹下 docker compose down docker compose up -d https://github.com/langgenius/dify/issues/17677...

编程日记 2025/8/16 0:03:00

2025 年第十五届 MathorCup 数学应用挑战赛 A 题：汽车风阻预测

A 题：汽车风阻预测在空气动力学领域，空气阻力对汽车以及航空航天工业中载具的性能和效率有着至关重要的影响。以往的研究表明，预测这种阻力需要借助先进的工业仿真软件进行大规模流体力学模拟仿真，而该模拟过程不仅算法复杂…...

编程日记 2025/8/15 23:58:03

AI Agents系列之AI代理架构体系

1. 引言智能体架构是定义智能体组件如何组织和交互的蓝图，使智能体能够感知其环境、推理并采取行动。本质上，它就像是智能体的数字大脑——集成了“眼睛”（传感器）、“大脑”（决策逻辑）和“手”（执行器），用于处理信息并采取行动。选择正确的架构对于构建有效的智能…...

编程日记 2025/8/15 1:10:27

使用Java动态数据生成PDF报告：简化您的报告导出流程

在当今的数据驱动世界中，能够快速且有效地将数据转化为可视化的报告是一项宝贵的技能。无论是商业分析、项目管理还是学术研究，PDF报告都是分享和存档信息的理想格式。在这篇博客中，我们将探讨如何使用Java编程语言结合iText库来动态生成包含…...

编程日记 2025/8/16 0:01:52

Sqlite3交叉编译全过程

Sqlite3交叉编译全过程一、概述二、下载三、解压四、配置五、编译六、安装七、验证文件类型八、移植8.1、头文件sqlite3.h8.2、动态链接库移植8.3、静态态链接库移植九、验证使用9.1. 关键函数说明十、触发器使用十一、sqlite表清空且恢复id值十二、全文总结一、概述 SQLi…...

编程日记 2025/8/13 14:08:20

Qt QThread 两种线程管理方法

在 Qt 中，QThread 有两种常见的用法，分别对应不同的线程管理模型。这两种方法各有优缺点，适用于不同的场景： 1. 子类化 QThread（继承 QThread，重写 run() 方法）这是传统的线程用法，类似于 Java 或 C++ 标准库中的线程模型。通过继承 QThread 并重写 run() 方法，将需…...

编程日记 2025/8/15 23:56:12

React 中如何获取 DOM：用 useRef 操作非受控组件

📌 场景说明在写 React 的时候，通常我们是通过“受控组件”来管理表单元素，比如用 useState 控制 <input> 的值。但有些时候，控制的需求只是临时性的，或者完全不需要重新渲染组件，这时候直接访问…...

编程日记 2025/8/13 11:23:59

GoogleCodeUtil.java

Google动态验证码实现 GoogleCodeUtil.java package zwf;import java.io.UnsupportedEncodingException; import java.net.URLEncoder; import java.nio.charset.StandardCharsets; import java.security.SecureRandom;/** https://mvnrepository.com/artifact/commons-codec/…...

编程日记 2025/8/11 22:47:00

一.深度优先遍历：

1.树的深度优先遍历：

2.图的深度优先遍历：

3.模拟图的深度优先遍历的执行过程：

4.图的深度优先遍历算法存在的问题与优化：

二.图的深度优先遍历算法的空间复杂度：

如上图，图的深度优先遍历算法的空间复杂度主要取决于DFS函数的递归调用。

1.最坏的情况：

2.最好的情况：

3.注意：做题时，题目问图的深度优先遍历算法的空间复杂度，没有特别说明的情况下，要答O( |V| )即最坏的情况。

三.图的深度优先遍历算法的时间复杂度：

核心：无论是BFS还是DFS，计算时间复杂度都可以简化为计算访问各个顶点所需要的时间加探索各条边/弧所需要的时间

1.如果图采用邻接矩阵存储：

2.如果图采用邻接表存储：

四.深度优先遍历序列：从哪一个顶点开始遍历（入栈），遍历结束时就是哪个顶点最后一个出栈（先进后出）

1.从2号顶点出发进行深度优先遍历整个图：

2.从3号顶点出发进行深度优先遍历整个图：（详细遍历过程）

3.从1号顶点出发进行深度优先遍历整个图：

4.细节：当图使用邻接表存储的话，由于邻接表的表现方式不唯一即顶点对应的链表中顶点号顺序不固定，因此如果从某一个顶点出发深度优先遍历得到的图的序列也可能不一样

5.总结：关于图采用邻接表存储

五.深度优先生成树：

六.深度优先生成森林：

七.图的遍历与图的连通性：

1.无向图：

2.有向图：

八.总结：

相关文章：