机器学习中的距离度量与优化方法：从曼哈顿距离到梯度下降

目录

• 前言
• 一、曼哈顿距离(Manhattan Distance)：
• 二、切比雪夫距离 (Chebyshev Distance)：
• 三、 闵可夫斯基距离(Minkowski Distance)：
• 小结
• 四、余弦距离(Cosine Distance)
• 五、杰卡德距离(Jaccard Distance)
• 六、交叉验证方法
• 6.1 HoldOut Cross-validation（Train-Test Split）（保留交叉验证）
• 6.2 K-折交叉验证（K-fold Cross Validation，记为K-CV）
• 七、前向传播与损失函数反向传播的学习率与梯度下降
• 7.1 求导法则
• 7.1.1 导数含义
• 7.1.1.1举例子理解
• 例1：速度(小车在马路上匀速的前进)：
• 例2：速度(小车在马路上非匀速的前进)：
• 7.2 什么是导数
• 7.3 常见的导数
• 7.3.1线性函数的导数：
• 7.3.2 其它常见的导数：
• 7.2 不可微函数
• 7.4 导数的求导法则
• 7.4.1 导数求导法则的定义：
• 7.4.2 两个函数相加的导数
• 7.4.3 两个函数乘积的导数
• 7.4.4 两个函数的比值的导数
• 7.5 复合求导运算：
• 7.6 链式求导法则：
• 7.7 偏导数
• 7.7.1 偏导数定义
• 7.8 梯度
• 八、前向传播与损失函数
• 8.1 前向传播与损失函数理论讲解
•  8.1.1 前向传播的定义
• 8.1.2 前向传播的过程
• 8.1.3 前向传播的作用
• 8.1.4 损失函数的概念：
• 8.2 基础原理讲解
• 8.2.1 案例导入
• 8.2.2 前向计算
• 8.2.3 单点误差
• 8.2.4 损失函数：均方差
• 总结

---

前言

书接上文

KNN算法深度解析：从决策边界可视化到鸢尾花分类实战-CSDN博客文章浏览阅读660次，点赞11次，收藏10次。本文系统讲解了KNN算法的决策边界形成机制、Scikit-learn实现细节及鸢尾花分类实战，涵盖K值选择对边界的影响、API参数解析、数据预处理（归一化/标准化）和数据集划分方法，通过代码示例和可视化分析帮助读者掌握KNN的核心应用技巧。https://blog.csdn.net/qq_58364361/article/details/147201792?spm=1011.2415.3001.10575&sharefrom=mp_manage_link

---

一、曼哈顿距离(Manhattan Distance)：

定义：曼哈顿距离是计算两点之间水平线段或垂直线段的距离之和，也称为城市街区距离或L1距离

eg:

在曼哈顿街区要从一个十字路口开车到另一个十字路口，驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是“曼哈顿距离”。曼哈顿距离也称为“城市街区距离”(City Block distance)。

距离公式：

缺点：由于它不是可能的最短路径，它比欧几里得距离更有可能给出一个更高的距离值，随着数据维度的增加，曼合顿距离的用处也就越小。

#曼哈顿距离
import numpy as np#计算曼哈顿距离
x = [1, 2]  # 点x的坐标
y = [3, 4]  # 点y的坐标#法一：使用循环计算曼哈顿距离
def manhattan_distance(x, y):"""计算两个点之间的曼哈顿距离参数:x (list): 第一个点的坐标列表y (list): 第二个点的坐标列表返回:int/float: 两个点之间的曼哈顿距离"""sum = 0for a, b in zip(x, y):sum += abs(a - b)return summd = manhattan_distance(x, y)  # 调用函数计算曼哈顿距离
print(md)  # 输出结果#法二：使用numpy计算曼哈顿距离
def manhattan_distance2(x, y):"""使用numpy计算两个点之间的曼哈顿距离参数:x (list): 第一个点的坐标列表y (list): 第二个点的坐标列表返回:int/float: 两个点之间的曼哈顿距离"""x_1 = np.array(x)  # 将列表转换为numpy数组y_1 = np.array(y)  # 将列表转换为numpy数组return np.sum(np.abs(x_1 - y_1))  # 使用numpy函数计算绝对差的和md2 = manhattan_distance2(x, y)  # 调用函数计算曼哈顿距离
print(md2)  # 输出结果

D:\python_huanjing\.venv1\Scripts\python.exe C:\Users\98317\PycharmProjects\study_python\机器学习\day4_15.py 
4
4进程已结束，退出代码为 0

---

二、切比雪夫距离 (Chebyshev Distance)：

定义：切比雪夫距离是计算两点在各个坐标上的差的绝对值的最大值。

国际象棋中，国王可以直行、横行、斜行，所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步？这个距离就叫切比雪夫距离。

缺点：切比雪夫距离通常用于非常特定的用例，这使得它很难像欧氏距离那样作通用的距离度量

#切比雪夫距离
import numpy as np#计算切比雪夫距离
x = [1, 2]  # 第一个点的坐标
y = [4, 6]  # 第二个点的坐标#第一种方式计算切比雪夫距离
def chebyshev_distance(x, y):"""计算两个点之间的切比雪夫距离（使用纯Python实现）参数:x (list): 第一个点的坐标列表y (list): 第二个点的坐标列表返回:float: 两个点之间的切比雪夫距离"""max_list = []for a, b in zip(x, y):max_list.append(abs(a - b))return max(max_list)cd = chebyshev_distance(x, y)
print(f"cd:{cd}")#第2种方法
def chebyshev_distance1(x, y):"""计算两个点之间的切比雪夫距离（使用NumPy实现）参数:x (list): 第一个点的坐标列表y (list): 第二个点的坐标列表返回:float: 两个点之间的切比雪夫距离"""x_1 = np.array(x)y_1 = np.array(y)return np.max(np.abs(x_1 - y_1))cd1 = chebyshev_distance1(x, y)
print(f"cd1 :{cd1}")

D:\python_huanjing\.venv1\Scripts\python.exe C:\Users\98317\PycharmProjects\study_python\机器学习\day4_15.py 
cd:4
cd1 :4进程已结束，退出代码为 0

---

三、 闵可夫斯基距离(Minkowski Distance)：

两个n维变量a(x11,x12,…,x1n)与b(x21,x22,…,x2n)间的闵可夫斯基距离定义为：

其中p是一个变参数：

当p=1时，就是曼哈顿距离；

当p=2时，就是欧氏距离；

当p→∞时，就是切比雪夫距离。

根据p的不同，闵氏距离可以表示某一类/种的距离。

import numpy as npx = [1, 2]  # 第一个向量
y = [4, 6]  # 第二个向量# 计算闵可夫斯基距离
def minkowski_distance(x, y, p):"""计算两个向量之间的闵可夫斯基距离参数:x -- 第一个输入向量y -- 第二个输入向量p -- 距离参数返回:两个向量之间的闵可夫斯基距离当p=1时返回曼哈顿距离当p=2时返回欧式距离当p趋近无穷时返回切比雪夫距离"""x = np.array(x)  # 转换为numpy数组y = np.array(y)  # 转换为numpy数组if p == 1 or p == 2:  # 当p为1或2时使用标准闵可夫斯基公式test = np.power(np.sum(np.power(np.abs(x - y), p)), 1 / p)return testelse:  # 其他情况返回切比雪夫距离(即最大绝对差)return np.max(np.abs(x - y))md = minkowski_distance(x, y, 1)  # 计算距离
print("曼哈顿距离:", md)  # 输出结果
md = minkowski_distance(x, y, 2)  # 计算距离
print("欧氏距离：", md)  # 输出结果
md = minkowski_distance(x, y, 3)  # 计算距离
print("切比雪夫距离：", md)  # 输出结果

D:\python_huanjing\.venv1\Scripts\python.exe C:\Users\98317\PycharmProjects\study_python\机器学习\day4_15.py 
曼哈顿距离: 7.0
欧氏距离： 5.0
切比雪夫距离： 4进程已结束，退出代码为 0

---

小结

1 闵氏距离，包括曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点:

e.g. 二维样本(身高[单位:cm],体重[单位:kg]),现有三个样本：a(180,50)，b(190,50)，c(180,60)。

a与b的闵氏距离（无论是曼哈顿距离、欧氏距离或切比雪夫距离）等于a与c的闵氏距离。但实际上身高的10cm并不能和体重的10kg划等号。

2 闵氏距离的缺点：

 (1)将各个分量的量纲(scale)，也就是“单位”相同的看待了;

 (2)未考虑各个分量的分布（期望，方差等）可能是不同的。
 (3) 使用参数p实际上可能会很麻烦

---

四、余弦距离(Cosine Distance)

定义：余弦相似度是两个向量之间的夹角余弦值，表示两个向量的方向差异，而不是长度差异。

二维空间中向量A(x1,y1)与向量B(x2,y2)的夹角余弦公式：

两个n维样本点a(x11,x12,…,x1n)和b(x21,x22,…,x2n)的夹角余弦为：

即：

缺点：余弦相似度无法捕捉向量的幅度信息，只考虑方向。

import mathx = [1, 1]
y = [2, -2]#计算余弦距离
def cosine_distance(x, y):"""计算两个向量之间的余弦距离参数:x (list): 第一个向量y (list): 第二个向量返回:float: 余弦相似度值，范围[0,1]"""#分子为0fz = 0#分母为0fm_x = 0fm_y = 0for a, b in zip(x, y):#分子：向量点积fz = fz + a * b#分母：向量模的乘积fm_x = fm_x + a ** 2fm_y = fm_y + b ** 2fm = math.sqrt(fm_x) * math.sqrt(fm_y)if fz > 0:return fz / fmelse:return 0md = cosine_distance(x, y)
print(md)

D:\python_huanjing\.venv1\Scripts\python.exe C:\Users\98317\PycharmProjects\study_python\机器学习\day4_15.py 
0进程已结束，退出代码为 0

---

五、杰卡德距离(Jaccard Distance)

杰卡德相似系数(Jaccard similarity coefficient)：两个集合A和B的交集元素在A，B的并集中所占的比例，称为两个集合的杰卡德相似系数，用符号J(A,B)表示：

缺点：它受到数据大小的很大影响。大型数据集可能会对相似系数产生很大影响，因为数据量很大的话可能显著增加并集，同时保持交集不变。

杰卡德距离(Jaccard Distance)：与杰卡德相似系数相反，用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度：

import math
import numpy as np# 定义两个集合用于计算Jaccard相似系数
x_set = {1, 2, 3}
y_set = {2, 3, 4}def jaccrd_similarity_coefficient(x_set, y_set):"""计算两个集合之间的Jaccard相似系数参数:x_set: 第一个输入集合y_set: 第二个输入集合返回:float: Jaccard相似系数值，范围[0,1]当两个集合的并集为空时返回0"""# 计算交集大小intersection = len(set(x_set) & set(y_set))# 计算并集大小union = len(set(x_set) | set(y_set))if (union > 0):return intersection / unionreturn 0# 计算并打印Jaccard距离(1-相似系数)
jsc = jaccrd_similarity_coefficient(x_set, y_set)
print(f"jsc距离 :{1 - jsc}")

D:\python_huanjing\.venv1\Scripts\python.exe C:\Users\98317\PycharmProjects\study_python\机器学习\day4_15.py 
jsc距离 :0.5进程已结束，退出代码为 0

---

六、交叉验证方法

交叉验证是在机器学习建立模型和验证模型参数时常用的办法，一般被用于评估一个机器学习模型的表现。更多的情况下，我们也用交叉验证来进行模型选择(model selection)。

---

6.1 HoldOut Cross-validation（Train-Test Split）（保留交叉验证）

在这种交叉验证技术中，整个数据集被随机地划分为训练集和验证集。根据经验法则，整个数据集的近70%被用作训练集，其余30%被用作验证集。也就是我们最常使用的，直接划分数据集的方法。

---

6.2 K-折交叉验证（K-fold Cross Validation，记为K-CV）

模型的最终准确度是通过取k个模型验证数据的平均准确度来计算的。

#kfold交叉验证
from sklearn.model_selection import KFold
from sklearn.datasets import load_iris#获得数据
iris = load_iris()  # 加载iris数据集
# iris数据集，X是特征，Y是标签
X = iris.data  # 特征数据
Y = iris.target  # 目标标签
#申请一个对象
kf = KFold()  # 创建KFold对象，默认n_splits=5
for i, (train_index, test_index) in enumerate(kf.split(X)):"""执行K折交叉验证参数:train_index: 训练集索引数组test_index: 测试集索引数组输出:打印每折的训练集和测试集索引"""print(f"Fold{i + 1}")print(f"  Train: index={train_index}")print(f"  Test:  index={test_index}")

---

七、前向传播与损失函数反向传播的学习率与梯度下降

7.1 求导法则

从以下几个方面对求导法则进行介绍
1.导数的含义
2.常见的导数
3.不可微函数
4.导数的求导法则
5.偏导数
6.梯度
上面这6个方面的内容，让大家，掌握并理解求导法则，为后续学习机器学习算法的学习奠定基础。

---

7.1.1 导数含义

1.导数（Derivative），也叫导函数值。又名微商，是微积分中的重要基础概念。当函数y=f（x）的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f'(x0)或df(x0）/dx。

2.为什么要学习微积分或者说求导？

在机器学习(或者深度学习中)，绝大部分任务是构建一个损失函数，然后去最小化它，这个优化过程使用的就是微分，也可以说是求导。

---

7.1.1.1举例子理解

举2个非常简单、非常形象的例子，来理解一下导数为啥这样定义?

例1：速度(小车在马路上匀速的前进)：

一段路程共900米，小车均速走了30s。在17.5s时，小车运动多快？

问题1：在17.5s时，小车运动多快？

小学数学就学过速度，也叫速率，表示运动物体运动的距离随时间的变化率，s=vt的公式大家都会。

高中物理开始严谨一些，会更专业地区分“位移”“速度”（向量）和“距离”“速率”（无方向的标量），公式还是s=vt，但是表示的内容不同了。

这里我们就用简单的小学数学知识：

一辆小车在水平直线上匀速运动，它运动的速率v是不变的，因此运动的距离与时间成正比，也就是s=vt，这里，速率v就是距离s随t的变化率，距离s可以看作是时间t的函数。

为了方便起见，我们用x代表时间（代替t），f(x)代表距离，就是函数：f(x)=vx。

这里v就是函数的变化率，该函数的导数就是：f'(x)=v（后面会学如何求导）。

表示在任何时刻，小车距离变化的趋势都是v，时间每增加一个小小的x，距离就增加vx。

例2：速度(小车在马路上非匀速的前进)：

一段路程共900米，小车不均速走了30s。在17.5s时，小车运动多快？在0~30s之间，小车的平均运动多快？

通过在不同时间内对小车进行测距离得到下图

问题1：求在17.5s时，小车运动多快？
补充信息1：

在15s~20s之间，小车的平均运动速度多快？
补充信息2 给15s到20s之间的时间和距离关系表如下所示

通过上面的例子是不是间隔越小计算的速度越准确，下面用更通俗的讲解一下。

是不是用下面的公式就可以求17.5s的速度了？

两种不同的表示方法：

关于导数严谨的定义否存在的判别、计算和使用会在大学重头开始详细学习，高中只要简单地知道导数表示变化率、会求导数、会简单地用导数分析函数的性质即可。
函数f(x)的导数通常用f'(x)来表示，在f的右上角加上小撇。
当导数为正时，函数的变化率是正的，也就是递增的；
当导数为负时，函数的变化率是负的，也就是递减的；
当导数为0时，函数的变化率是0，也就是不增也不减，不变。

---

7.2 什么是导数

导数是函数，完整地叫应该是“导函数”，通常习惯叫“导数”，它是依附于原函数存在的函数。

导数表示函数的变化趋势：
●既可以表示函数整体的变化趋势；
●也可以表示部分的变化趋势
●还可以表示某个点的变化趋势。
导数也可以粗糙地理解为“函数在某处的切线的斜率”。

---

7.3 常见的导数

常数的表达式为：

---

7.3.1线性函数的导数：

线性函数的表达式为：

导数求解方法：

推导出：

2.3二次方程函数的导数：

y=x^2

其导数求解方法：

推导出：

7.3.2 其它常见的导数：

---

7.2 不可微函数

如果一个点存在导数，那么该点的函数会在该点微分。也就是说，如果要使函数在整个区间内保持微分则该区间中的每个点，都必须存在导数。

2.实际上，并不是所有的函数在每个点上都可以找到导数，这些函数称为：不可微函数。
eg: f(x)=|x|

证明过程：
函数f(x)=∣x∣在x=0处不可导的原因是因为该点的左导数和右导数不相等。具体来说：
●当x<0时，f(x)=−x，因此左导数为−1（即函数值随x的减小而增大）。
●当x>0时，f(x)=x，因此右导数为1（即函数值随x的增大而增大）。 由于左导数和右导数在这点上不相等（左导数为-1，右导数为1），根据可导性的定义，函数在x=0处不可导。这是因为可导的要求是函数在该点处连续，且左右导数相等，而绝对值函数在x=0处虽然连续，但左右导数的不一致性导致了不可导的情况。

---

7.4 导数的求导法则

7.4.1 导数求导法则的定义：

导数是函数值相对于自变量的瞬时变化率，求导数是一个取极限的过程。对于一个连续且可导的函数，其导数的定义如下

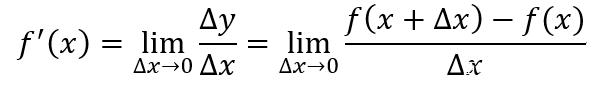
函数可导的前提是函数必须连续，对于连续函数，有下列等式成立

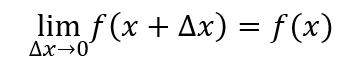
上式是函数在x处连续的定义。结合连续函数的定义和极限的运算性质，我们接下来推导导数运算法则。

---

7.4.2 两个函数相加的导数

设F(x)为两个可导函数的和

那么根据导数定义，F(x)的导数为

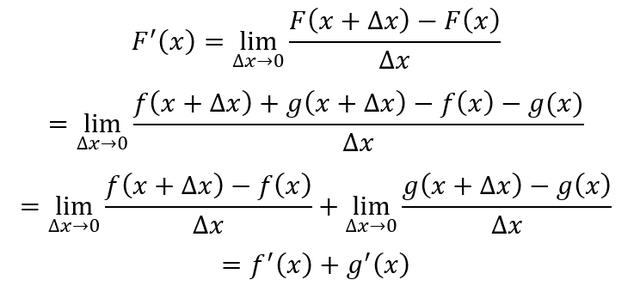
即两个可导函数的和的导数等于导数的和，导数运算减法同理。

---

7.4.3 两个函数乘积的导数

假设G(x)为两个可导函数的积

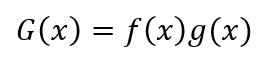
根据导数定义，G(x)的导数为

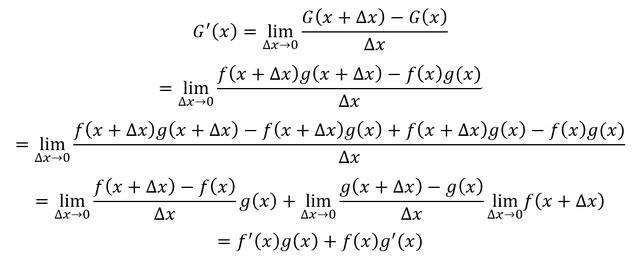
两个可导函数的乘积的导数的结果为

---

7.4.4 两个函数的比值的导数

设H(x)为两个可导函数的比值

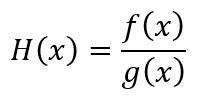
根据导数定义，那么H(x)的导数为

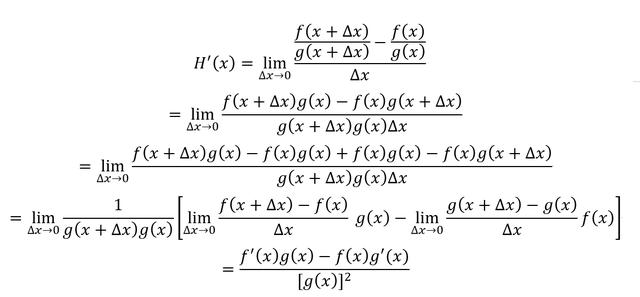
两个可导函数的比值的导数结果为

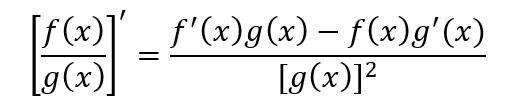
掌握推导过程可以帮助理解导数的定义和运算。

---

7.5 复合求导运算：

y=(sinx)^2

求导一下 y=2sinxcosx=sin2x

---

7.6 链式求导法则：

1）链式求导法则，也称为链式法则，是微积分中的一个基本法则，用于求解复合函数的导数。其基本公式为：如果y 是u 的函数，u 是x 的函数，即y=f(u) 且u=g(x)，则 y 对 x 的导数可以表示为：

这个公式表明，复合函数的导数等于内层函数对中间变量的导数乘以中间变量对自变量的导数。
2）链式求导法则的应用非常广泛，不仅限于一元函数的情况，还可以推广到多元函数的情况。在应用链式法则时，需要明确函数的复合情况及变量的关系，通过画出链式图，然后运用公式进行求导。

---

7.7 偏导数

7.7.1 偏导数定义

偏导数是一个多变量函数中关于其中一个变量的导数，同时保持其他变量恒定。

偏导例子
eg1:

对x求偏导数，y当作常数，结果为：

对y求偏导数，x当作常数，结果为：

eg2:

对x求偏导数，y当作常数，结果为：

对y求偏导数，x当作常数，结果为

---

7.8 梯度

梯度通俗讲就是偏导的集合

梯度的例子

八、前向传播与损失函数

以下2个方面对前向传播与损失函数进行介绍
1.前向传播与损失函数理论讲解
2.编程实例与步骤
上面这2方面的内容，让大家，掌握并理解前向传播与损失函数。

---

8.1 前向传播与损失函数理论讲解

 8.1.1 前向传播的定义

前向传播是指在机器学习算法中，从输入到输出的信息传递过程，具体来说，就是在数据输入后，经过一系列的运算后得到结果的过程。
输入x 经过一系列计算f(x) 得到y的过程
比如y=2x+3,这个公式，前向传播就是通过给定x,根据公式2x+3得到输出结果y的值的过程就是前向传播。

---

8.1.2 前向传播的过程

step1：输入层，输入数据首先需要进入输入层，每一个神经元都会接收一个信号(输入值(矩阵))

step2:输入层到隐藏层，输入层的输出作为下一层的输入(通常是隐藏层)，通过与权重相乘加上偏置项后进行非线性变换‌，使用激活函数对隐藏层的输出进行非线性变换，以引入非线性特性，增强模型的表达能力。

step3:隐藏层到输出层‌：将隐藏层的输出乘以隐藏层到输出层的权重矩阵，再加上偏置，计算输出层的输出。

---

8.1.3 前向传播的作用

对数据的输入逐步处理，提取对应的特征，并进行预测.

---

8.1.4 损失函数的概念：

损失函数（Loss Function）是用来衡量模型预测结果与实际结果之间的差异的一种函数。在机器学习中，损失函数通常被用来优化模型，通过最小化损失函数来提高模型的预测准确率。

---

8.2 基础原理讲解

8.2.1 案例导入

例子：

池塘里有7只蝌蚪，它们的体积（纵坐标）和时间（横坐标）有关，蝌蚪的体积随时间的变化。

自变量是时间x（以天为单位），因变量是蝌蚪的体积y（以毫升为单位）。

那么是否可以拟合一条线，来预测在未来的某个时间点，蝌蚪的体积可能会是多少。

---

8.2.2 前向计算

前向传播是指在一个机器学习算法中，从输入到输出的信息传递过程，具体来说，就是在数据输入后，经过一系列的运算后得到结果(模型预测结果)的过程。

w表示权重 b表示偏置

在本实验中，为了使用直线来拟合上面7个散点，可以用直线的斜截式方程来进行拟合，给出直线公式：

在前向计算中，为了简化运算，我们固定b的值为0，而w的值可以任意修改（范围0-2）。

w=0 w=0.8

也就是说，我们是用一条过原点的直线来拟合这些散点，在该组件中修改w的值可以实时看到直线与散点的位置关系。

---

8.2.3 单点误差

由下图可知，当w等于2的时候“拟合”这些散点和实际的坐标点y轴的差距，由图上的绿色虚线表示。绿色虚线表示每一个真实的数据点和预测的数据点的差距，也就是数据点损失。

---

8.2.4 损失函数：均方差

---

总结

        本文系统介绍了机器学习中常用的距离度量方法（曼哈顿距离、切比雪夫距离、闵可夫斯基距离、余弦距离、杰卡德距离）及其数学定义、Python实现与优缺点，并探讨了交叉验证方法（HoldOut与K折）的应用场景。此外，深入解析了前向传播与损失函数的核心原理，包括导数、偏导数、梯度等数学基础，以及链式求导法则在反向传播中的作用，最后通过蝌蚪体积预测案例演示了前向计算、单点误差和均方差损失函数的实际应用，为机器学习模型优化提供了理论支撑与实践指导。