当前位置：首页 > news >正文

专题三——二分查找

news 来源：原创 2025/9/13 14:42:57

一、二分查找

1、题目

2、解题思路

3、代码实现

4、时间复杂度

5、朴素二分法的模板总结

二、在排序数组中查找元素的第一个和最后一个位置

1、题目

2、题目解析

3、代码实现

4、模板总结（重点）

三、x的算法平方根

1、题目

2、题目解析

3、代码实现

四、搜索插入位置

1、题目

2、题目解析

3、代码实现

五、上峰数组的索引

1、题目

2、题目解析

3、代码实现

六、寻找峰值

1、题目

2、解题思路

3、代码编写

一、二分查找

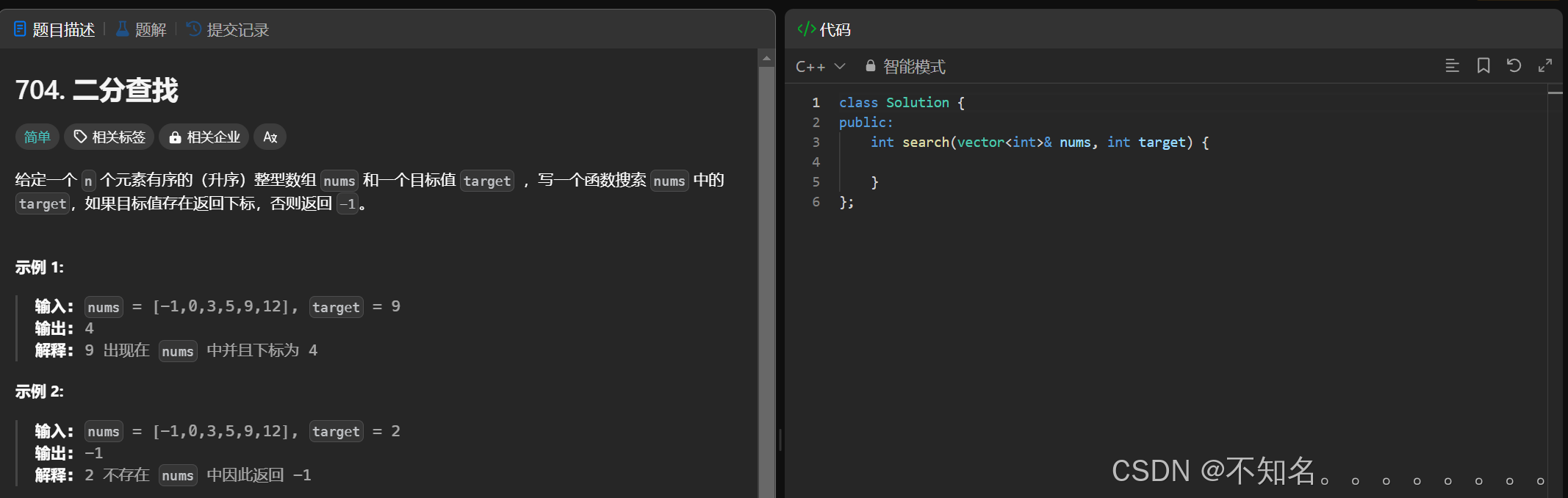
1、题目

二分查找

2、解题思路

方法一：暴力解法：我们直接遍历找到target

方法二：二分查找：我们观察到它是一个升序数组，具有二段性我们可以将它分为两段target一定可以在这两端中的一段，这样我们就可以直接省去一半的数值，然后我们再分二端又可以省去一半数值。。。

3、代码实现

暴力实现：

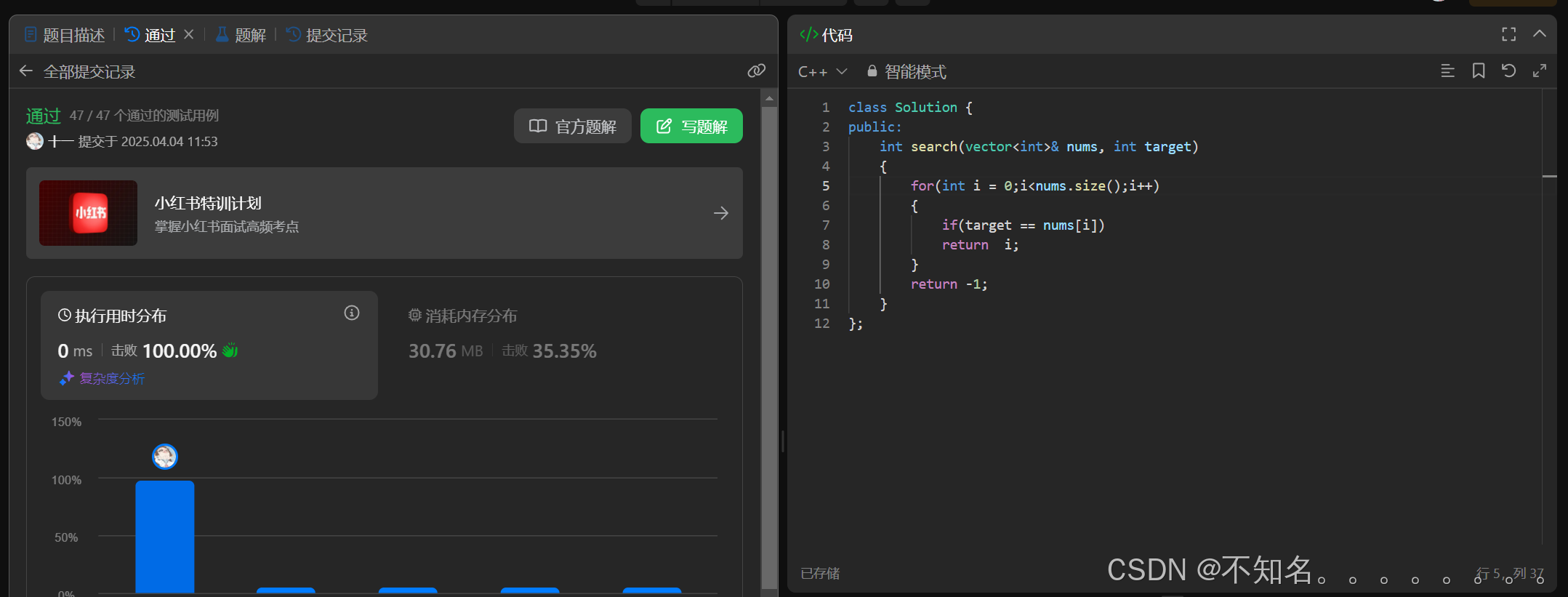
class Solution {
public:int search(vector<int>& nums, int target){for(int i = 0;i<nums.size();i++){if(target == nums[i])return  i;}return -1;}
};

二分查找：

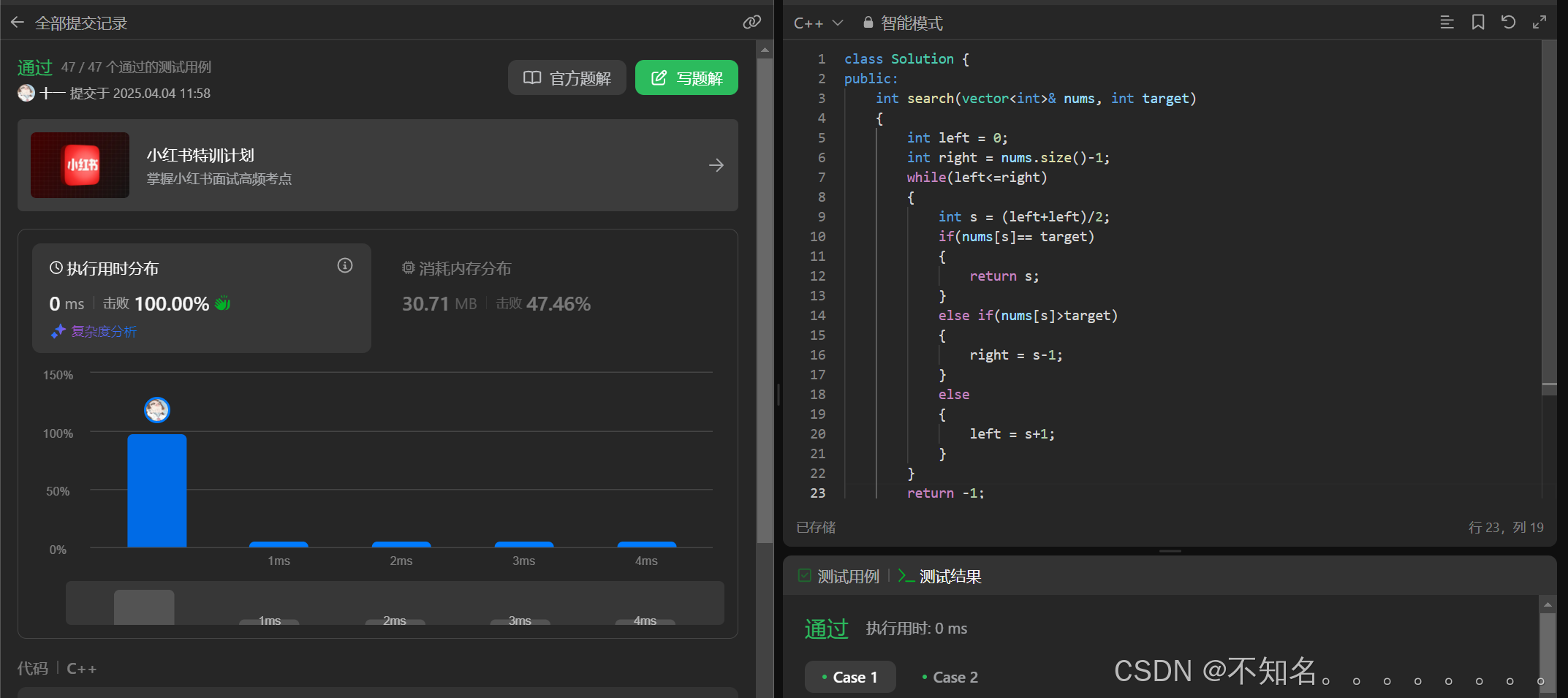
class Solution {
public:int search(vector<int>& nums, int target){int left = 0;int right = nums.size()-1;while(left<=right){int s = (left+left)/2;if(nums[s]== target){return s;}else if(nums[s]>target){right = s-1;}else{left = s+1;}}return -1;}
};

4、时间复杂度

如上图时间复杂度为logn

5、朴素二分法的模板总结

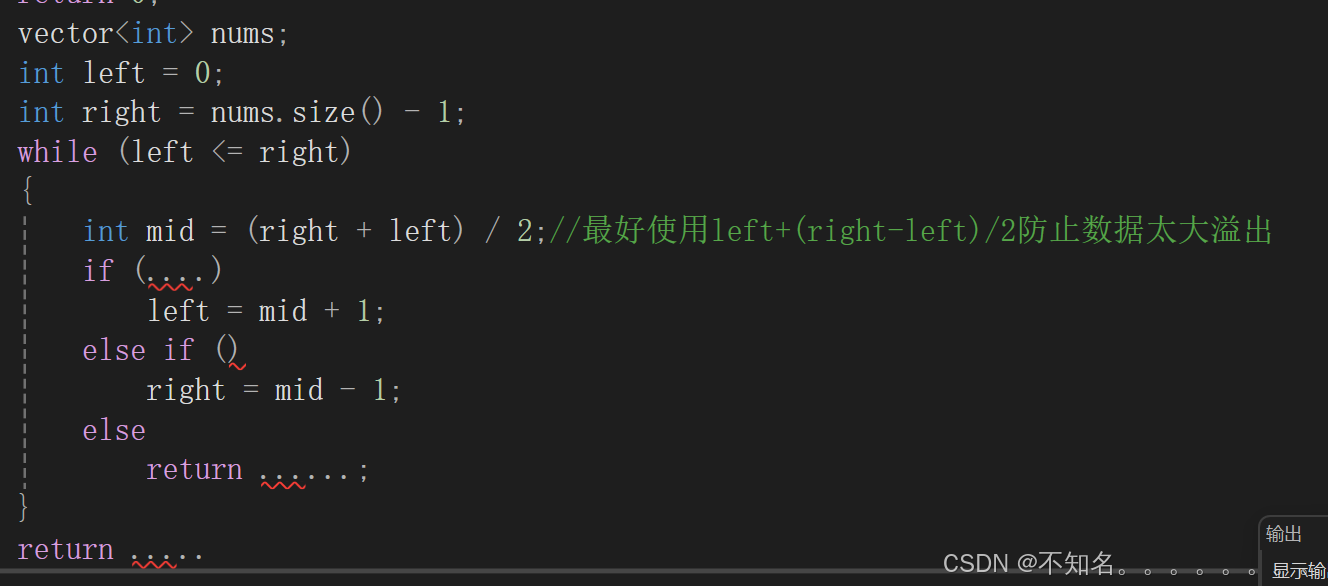
有一些人会使用left+(right-left+1)/2或者(right+left)/2其实和 (left+right)/2 和left+（right-left）/2的差别就是在数组个数为偶数的时候一个是前者，一个为后者，在朴素二分法这两者的效果是一样的

二、在排序数组中查找元素的第一个和最后一个位置

1、题目

https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/

2、题目解析

我们可以将题目化简成找target的左端点和右端点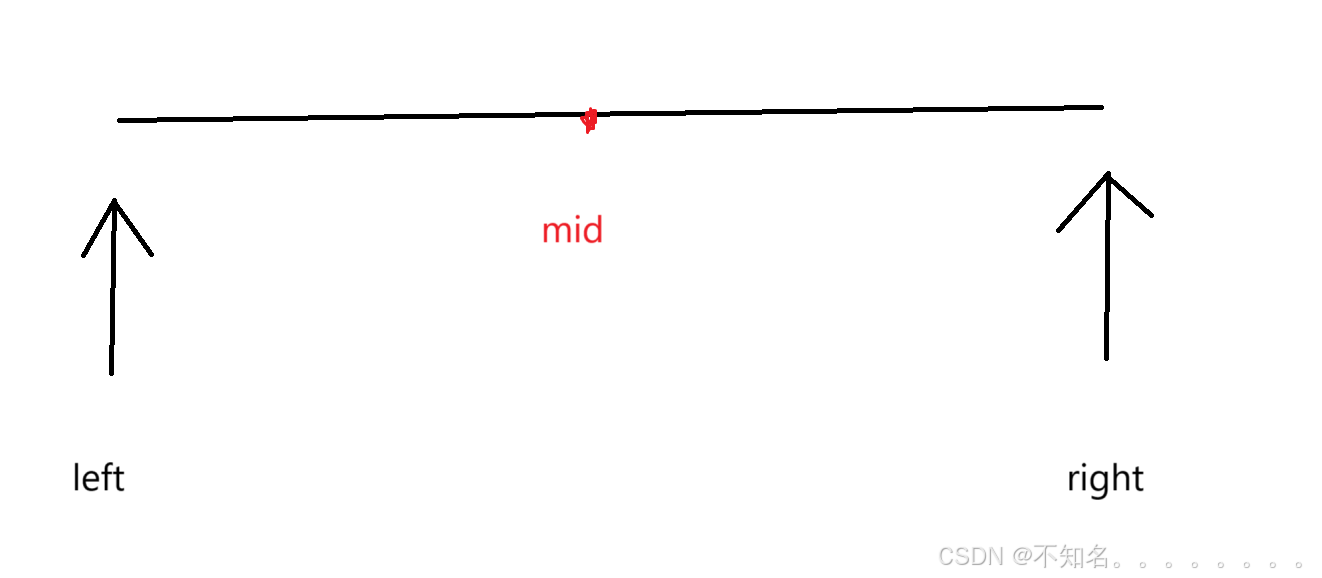

找左端点

我们像第一道题一样定义right,left求让中点值和target比较，当mid的值大于或者等于target 我们将right的移到mid(为什么要移到mid位置：因为防止mid的位置就是左端点的位置)

当mid的值小于target我们将left移到mid+1的位置

一直到left<right的时候结束循环：一般会出现三种情况 : left和right 区间中有我们最终的值

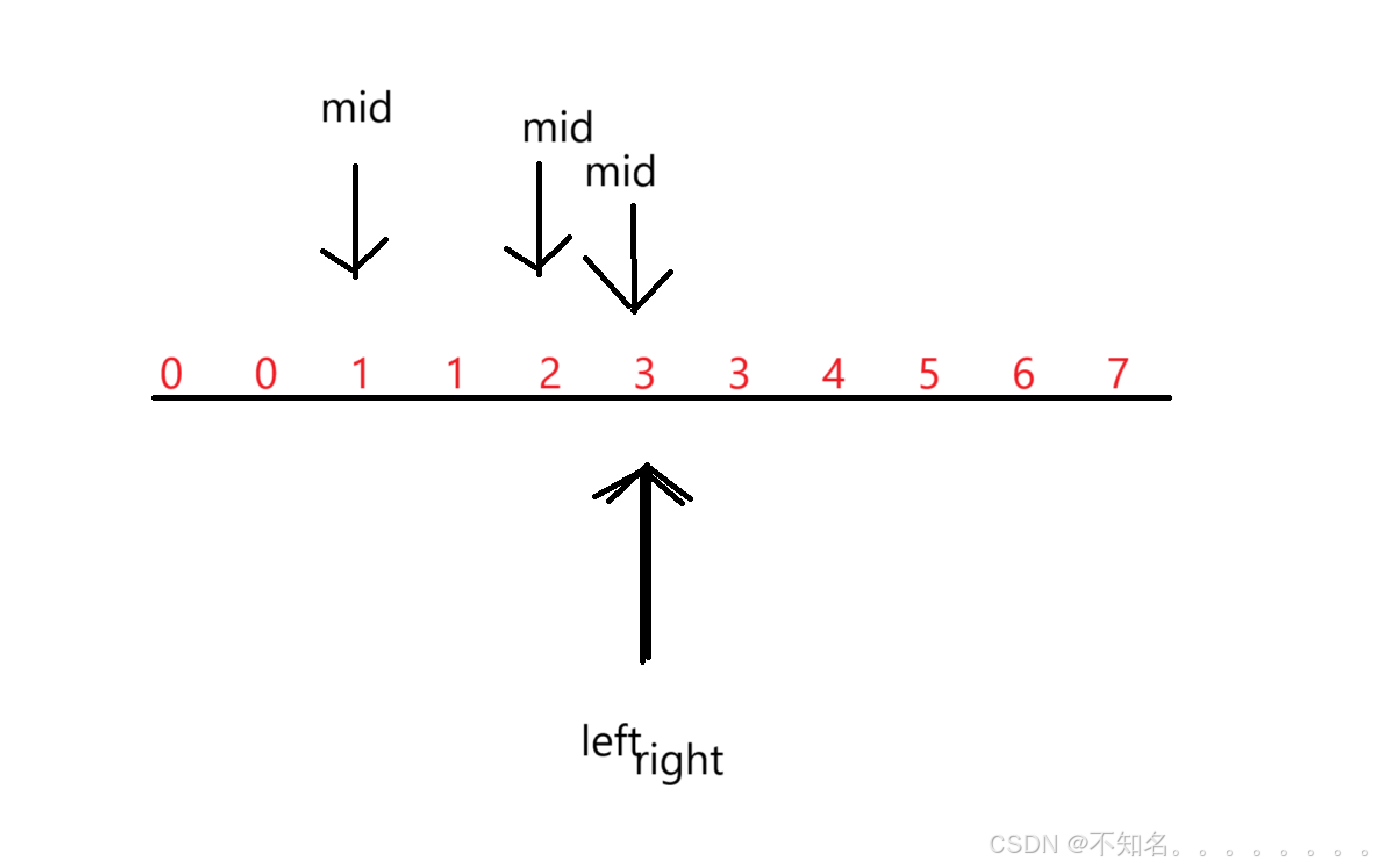
我们可以观察到一旦left=right的时候就是我们的最终结果

当left和right区域内全部大于t

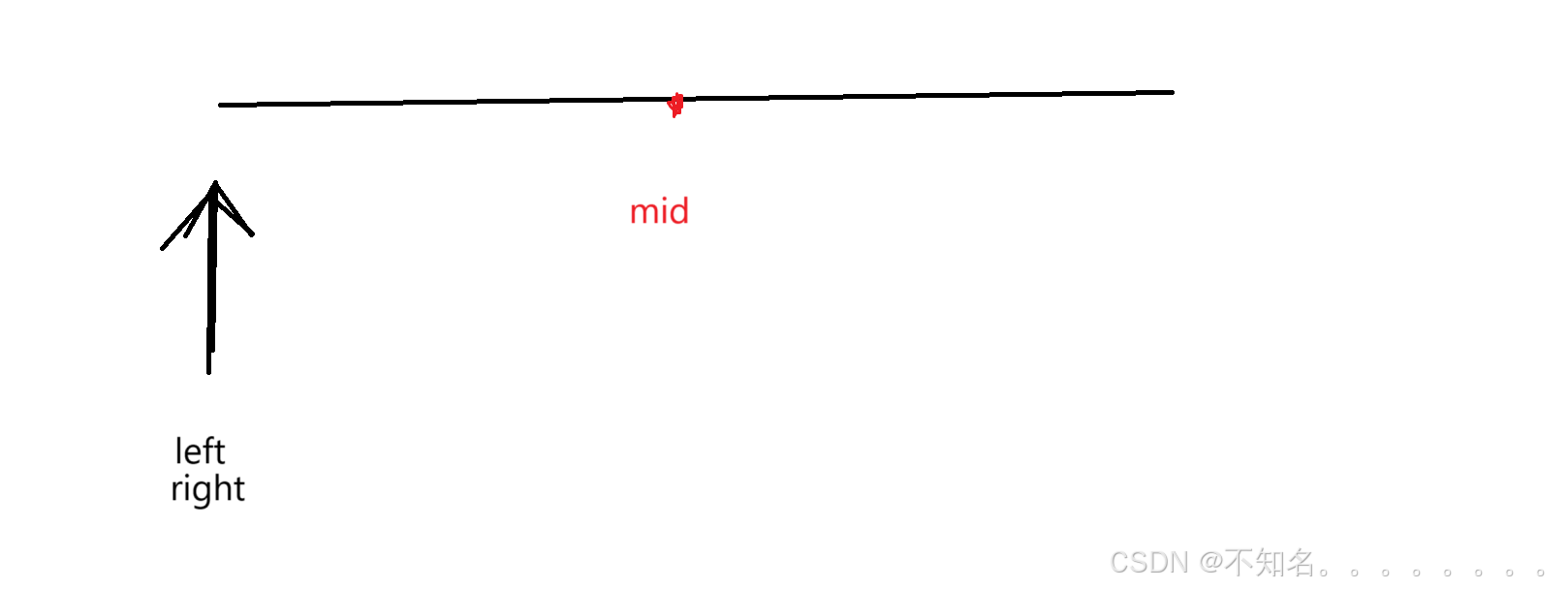
我们观察到当全部都是大于t的时候right会不停向left靠近，当他们相等的时候判断值就知道了有没有找到，不需要再进入循环，当left和right区域内小于t同理

综上所述我们的循环结束条件是left<right 1.left = right的时候就是最终结果，无需判断

2.一旦我们判断就是死循环

求中点的操作

mid = left+(right - left)/2 （不能使用left+(right -left+1)/2这个在偶数个数的时候会使用后面的值当作中点会进入死循环）

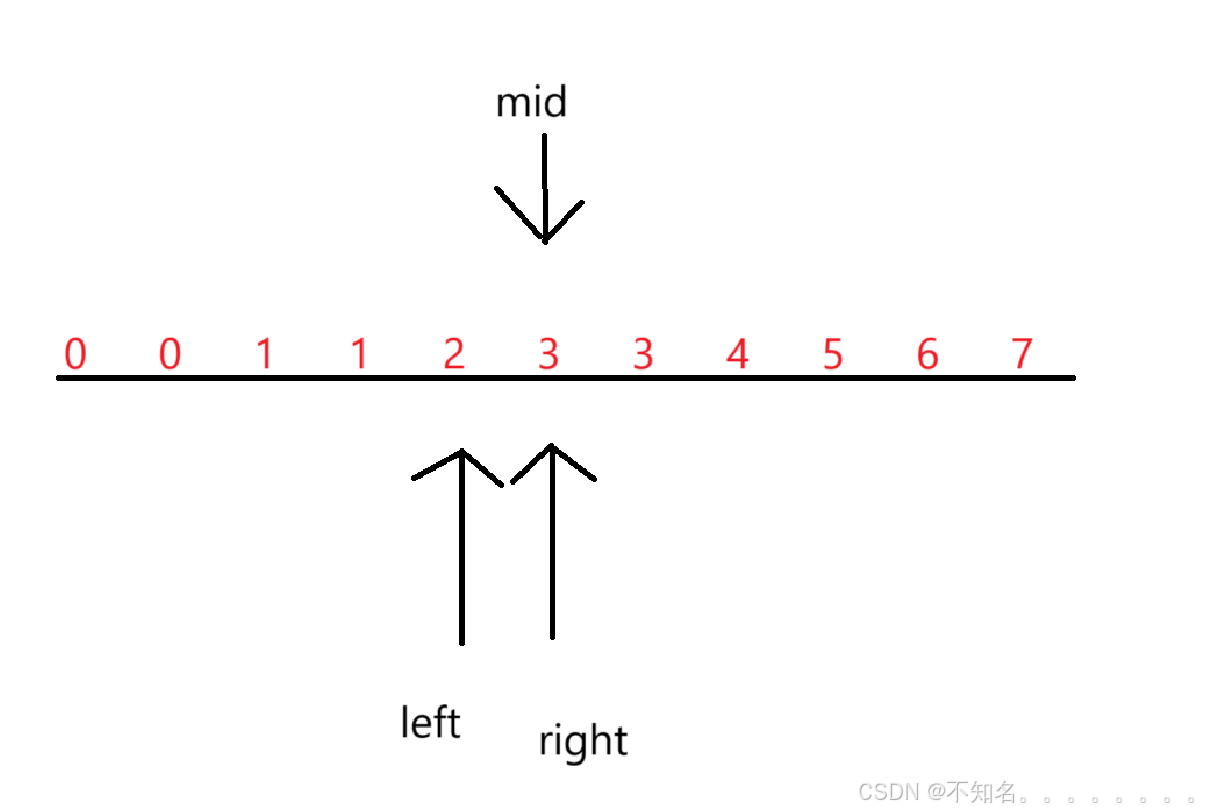
如上图如果选择后者为mid那么right会一直被停留在3,造成死循环。

找右端点

同理，不同的是当mid的值大于target我们将right的移到mid-1，如果mid的值小于或者等于target移动到将left移动到mid的位置，找中点结点使用的公式是left+(right -left+1)/2

3、代码实现

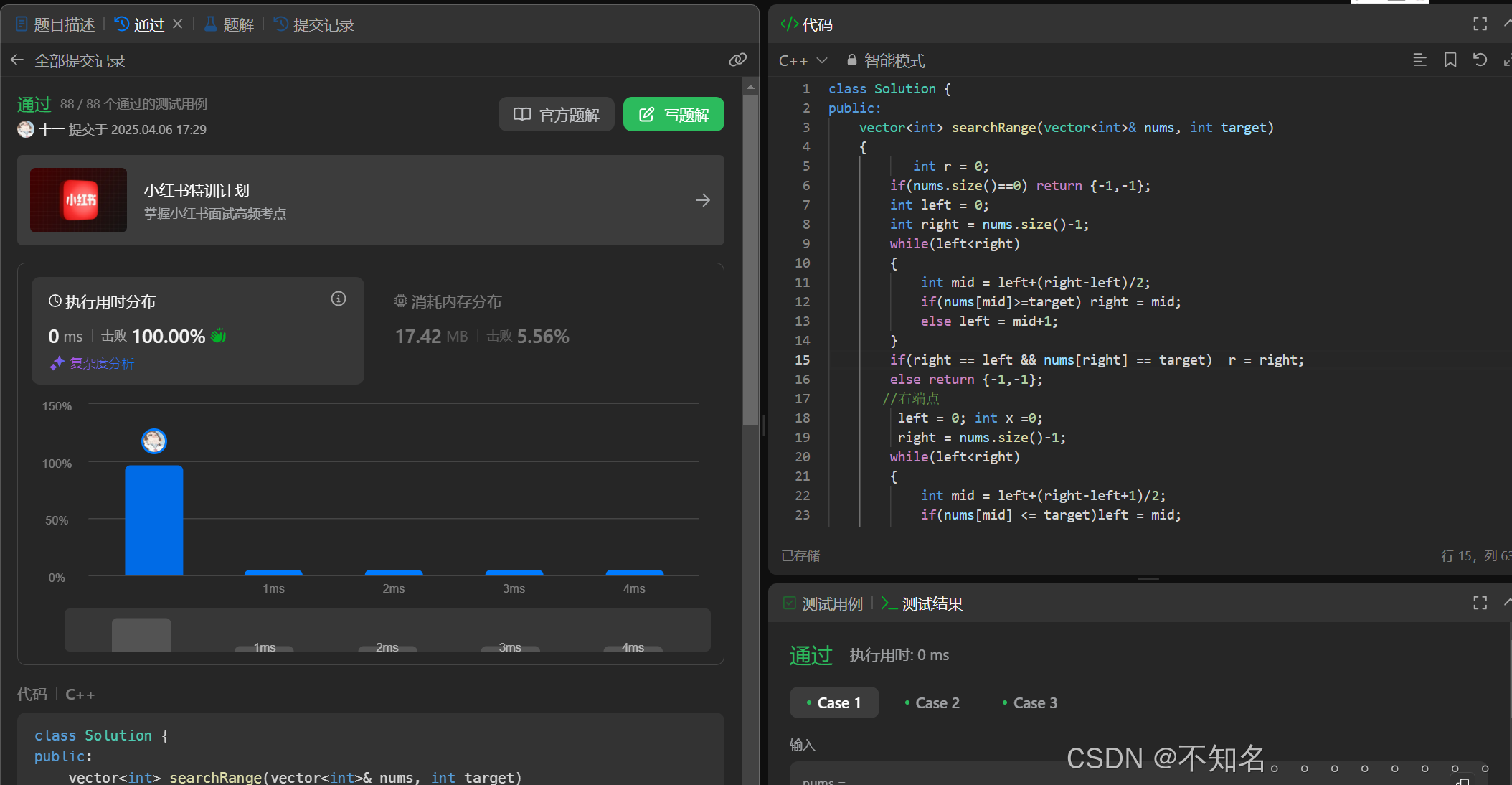
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target){   int r = 0;if(nums.size()==0) return {-1,-1};int left = 0; int right = nums.size()-1;while(left<right){int mid = left+(right-left)/2;if(nums[mid]>=target) right = mid;else left = mid+1;}if(right == left && nums[right] == target)r = right;elsereturn {-1,-1};left = 0; int x =0;right = nums.size()-1;while(left<right){int mid = left+(right-left+1)/2;if(nums[mid] <= target)left = mid;else  right = mid-1;}if(right == left && nums[right] == target)x = right;elsereturn {-1,-1};return {r,x};}
};

4、模板总结（重点）

这个模板只需要记住三角形的地方，其他地方我们可以快速判断（口诀：下面出现-1的时候，上面就+1）

三、x的算法平方根

1、题目

https://leetcode.cn/problems/sqrtx/

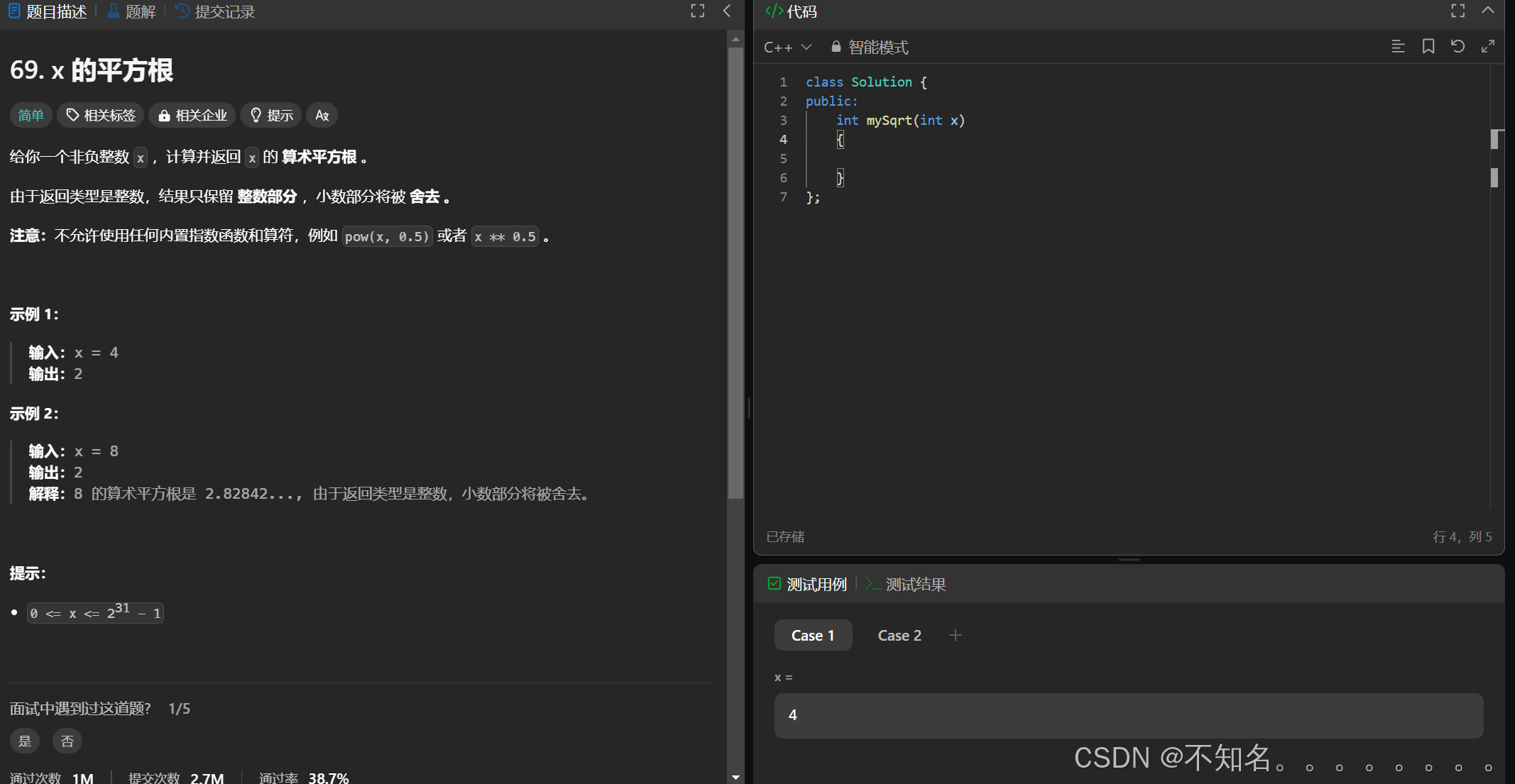
2、题目解析

暴力解法：循环遍历从1到它本身的值看那个值的平方满足这个条件，然后返回

二分算法：我们能观察他是具有二段性的（就是可以将这组数据一分为二，比如这个可以分为大于值的，和小于值的）和前集体一样，我们首先定义left 和right

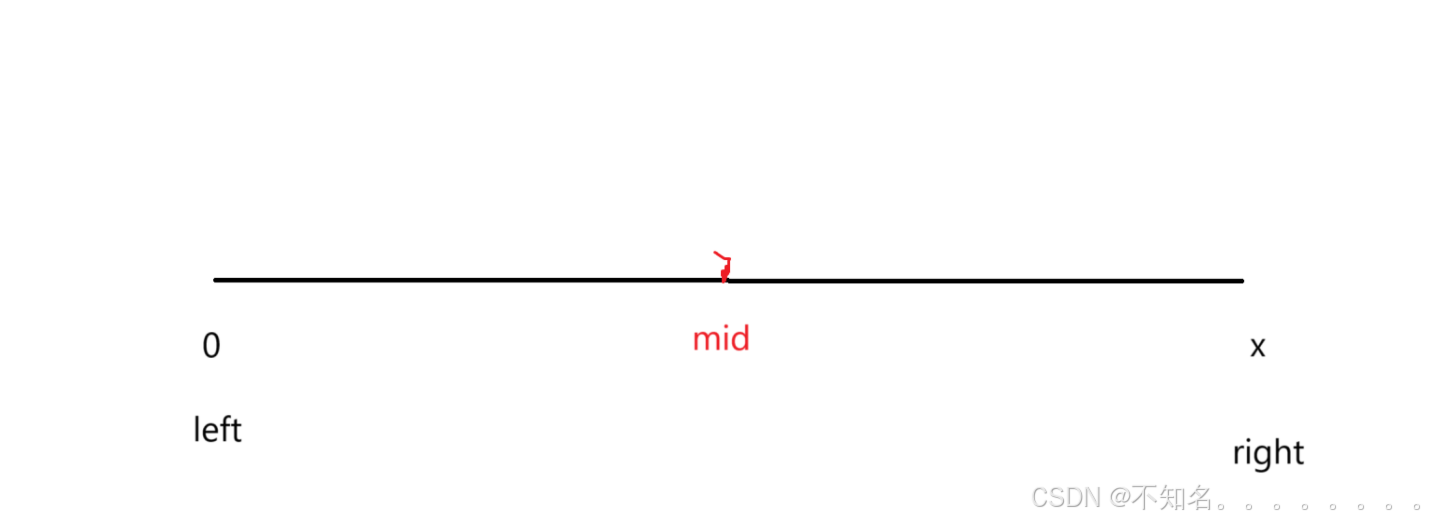
如果mid平方的值小于等于x left = mid,如果mid平方的值大于x right = left-1;

3、代码实现

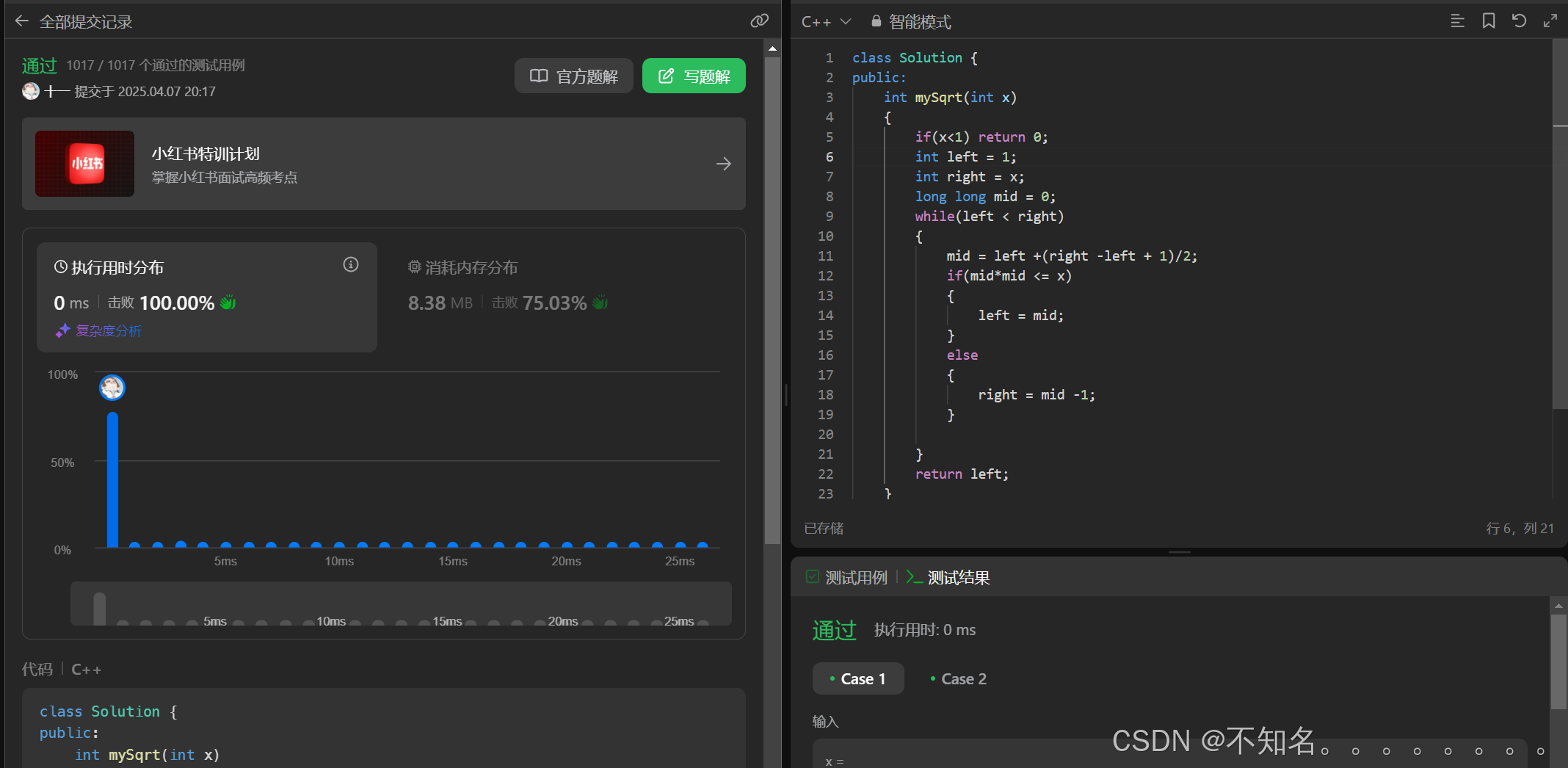
class Solution {
public:int mySqrt(int x){if(x<1)return 0;int left = 1;int right = x;while(left<right){long long mid = left+(right-left+1)/2;if(mid*mid <= x){left = mid;} else{right = mid-1;}}return right;}
};

四、搜索插入位置

1、题目

https://leetcode.cn/problems/search-insert-position/description/?envType=study-plan-v2&envId=top-100-liked

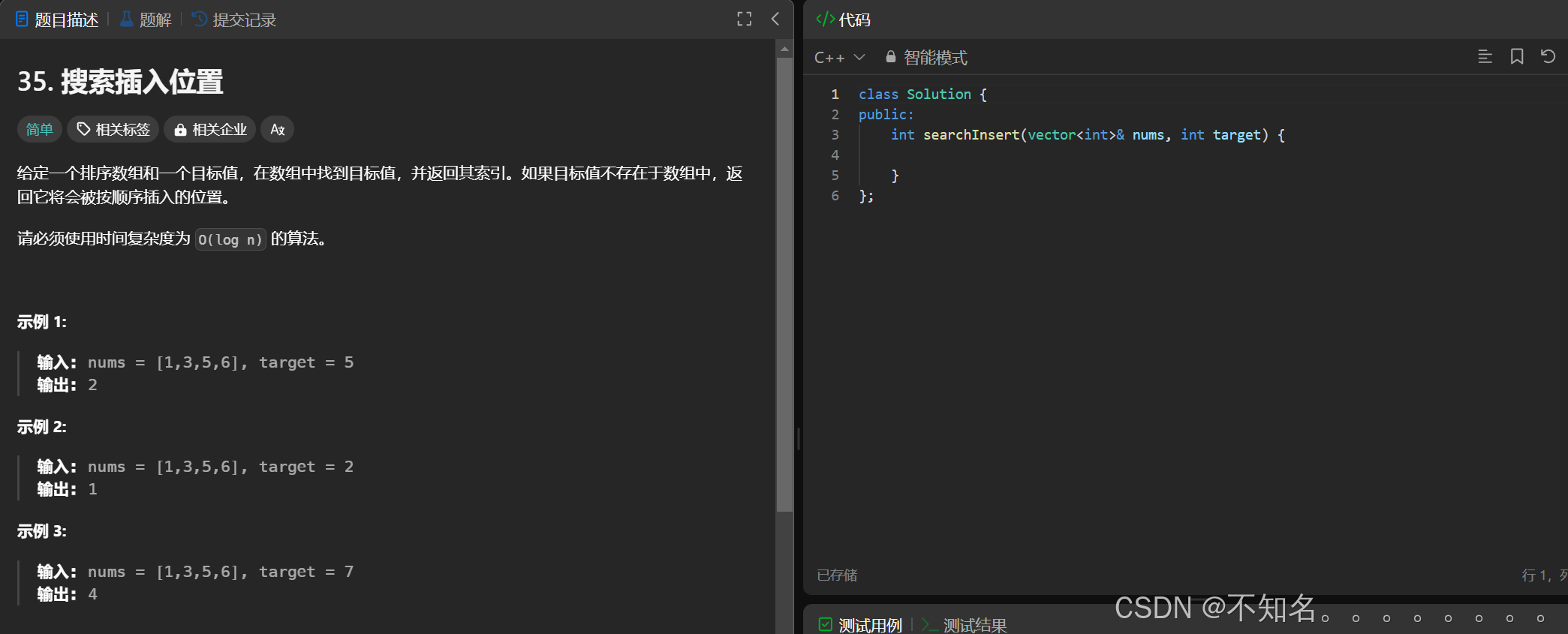
2、题目解析

暴力解法：遍历数组

二分算法：我们需要找到大于或等于目标值的值，这道题的思路和查找区间左端点的模板思路有高度的相似但是我们要注意的是这个算法只能解决目标值的大小在区间内的，例示例三我们需要让他返回后一个位置

3、代码实现

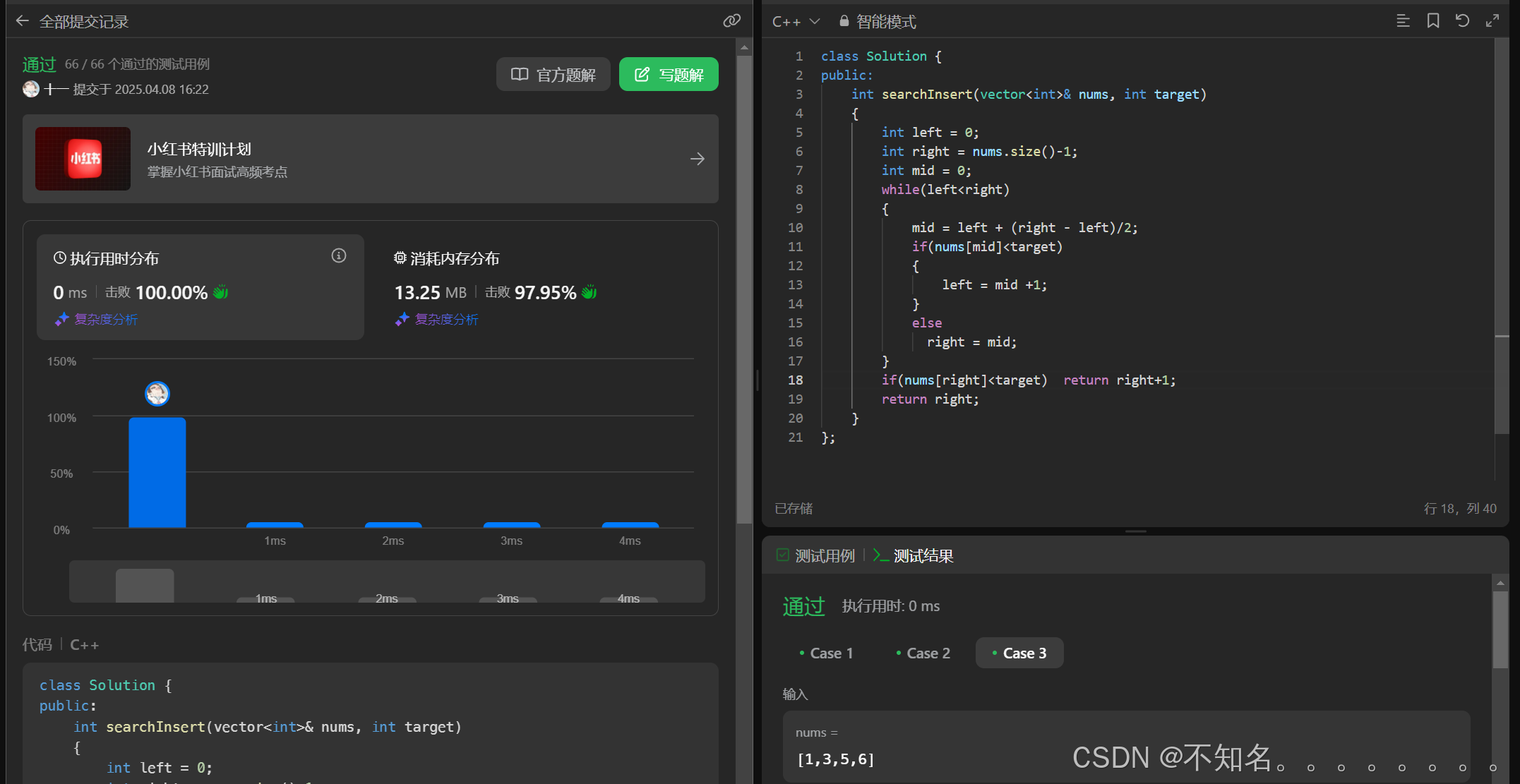
class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left = 0;int right = nums.size()-1;int mid = 0;while(left<right){mid = left + (right - left)/2;if(nums[mid]<target){left = mid +1;}elseright = mid;}if(nums[right]<target)  return right+1;return right;}
};

五、上峰数组的索引

1、题目

https://leetcode.cn/problems/B1IidL/description/

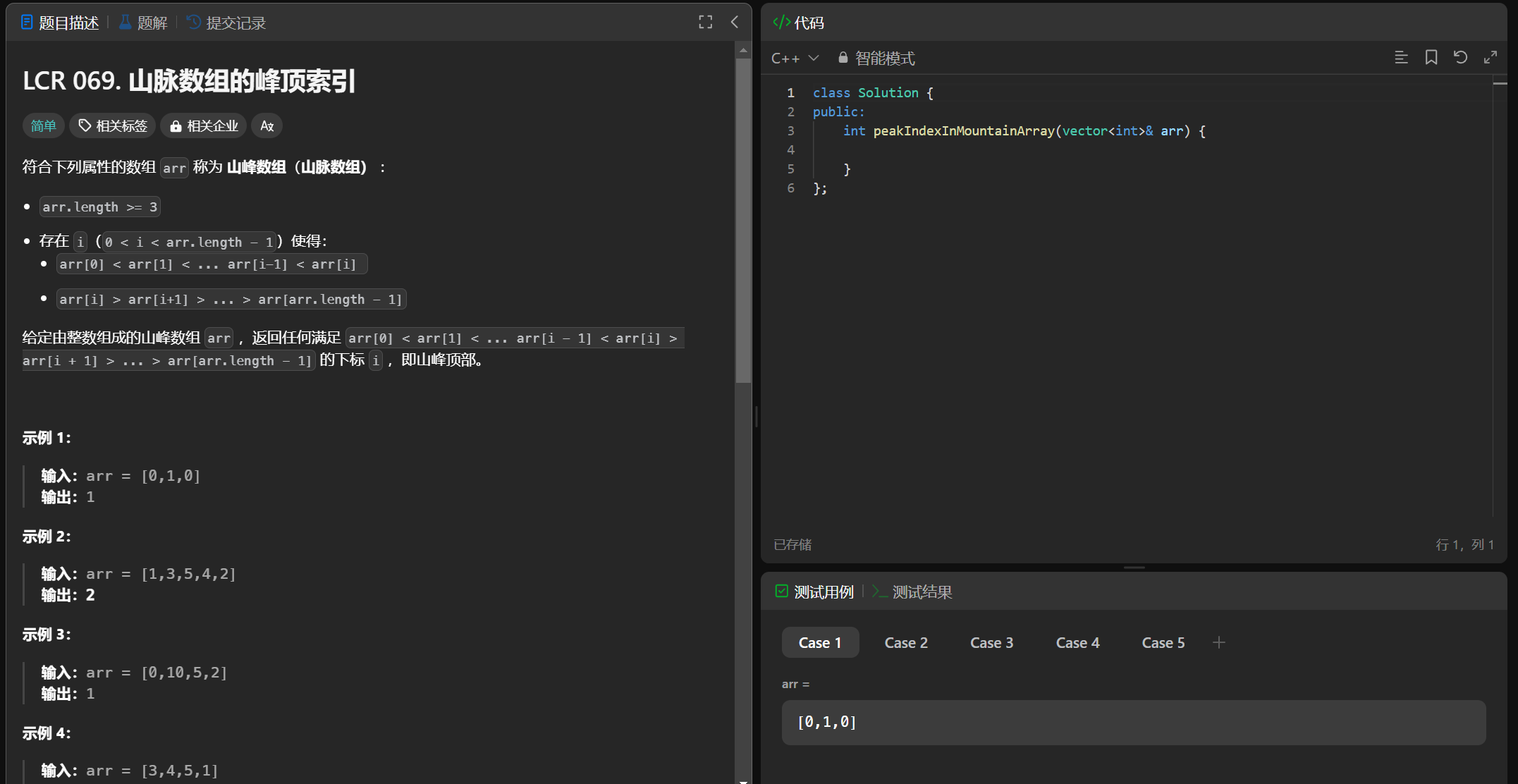
2、题目解析

（1）暴力方法：遍历数组，如果它的下一个比它的值要小就是山峰

（2）二分查找：我们发现我们可以将这个数组分为两部分（一部分arry[i]<arry[i+1]另外一部分 arry[i]>arry[i+1]）所以它符合二分性，可以使用二分查找

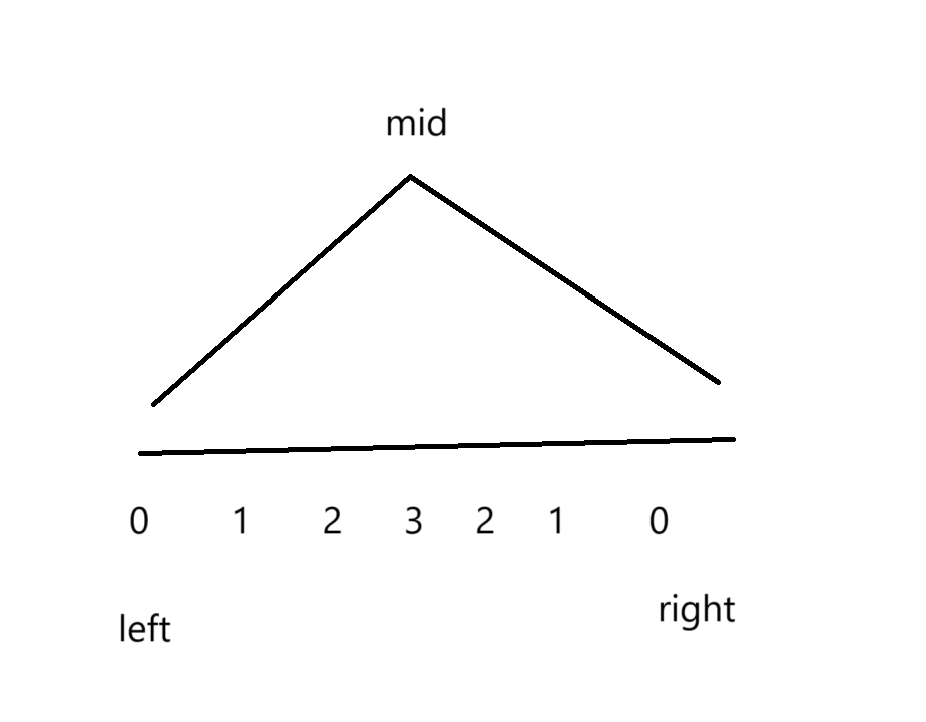如果arry[mid]>arry[mid-1] left = mid 如果arry[mid]<arry[mid-1 ] right = mid -1;

mid =left+ (right -left+1)/2;

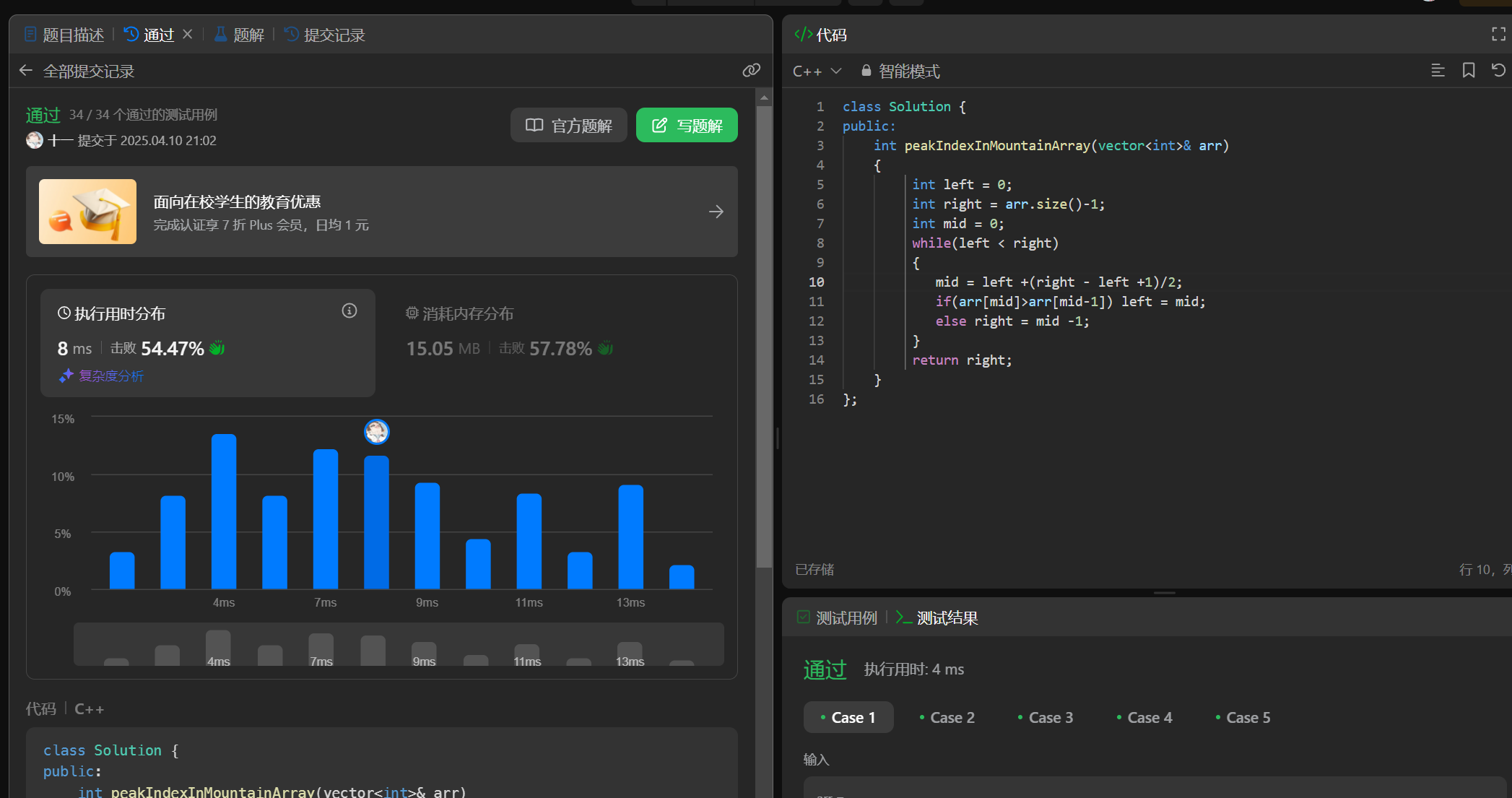
3、代码实现

class Solution {
public:int peakIndexInMountainArray(vector<int>& arr) {int left = 0;int right = arr.size()-1;int mid = 0;while(left < right){mid = left +(right - left +1)/2;if(arr[mid]>arr[mid-1]) left = mid;else right = mid -1;}return right;}
};

六、寻找峰值

1、题目

https://leetcode.cn/problems/find-peak-element/

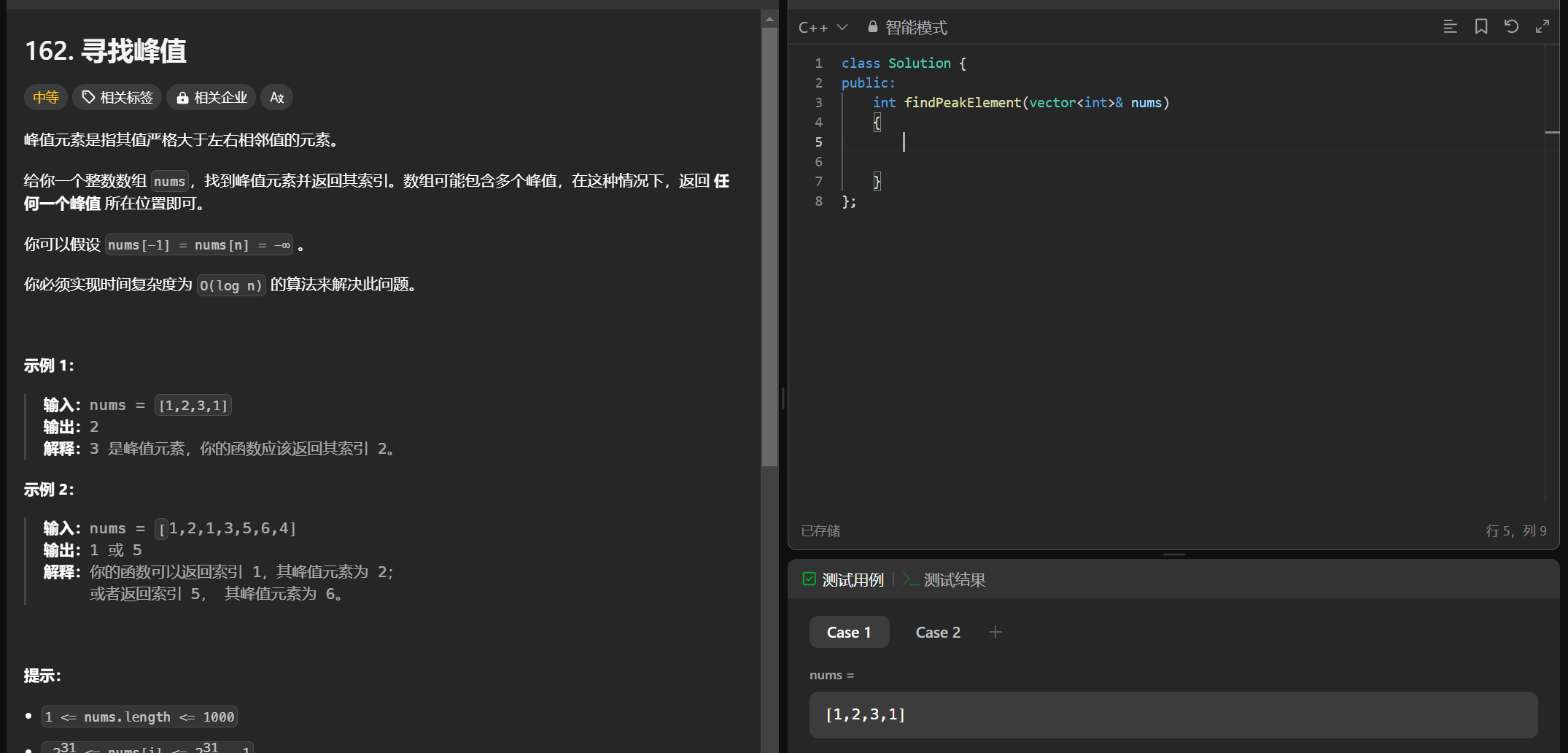
2、解题思路

（1）暴力解法：遍历整个数组如果nums[i+1]<nums[i] i就是封顶

（2）二分查找：我们可以发现虽然这个数据是无需的但是如果nums[i+1]<nums[i]在左边一定有峰值right = mid，如果nums[i+1]>nums[i]在右边一定有峰值left = mid+1（mid 表示中介按值）

3、代码编写

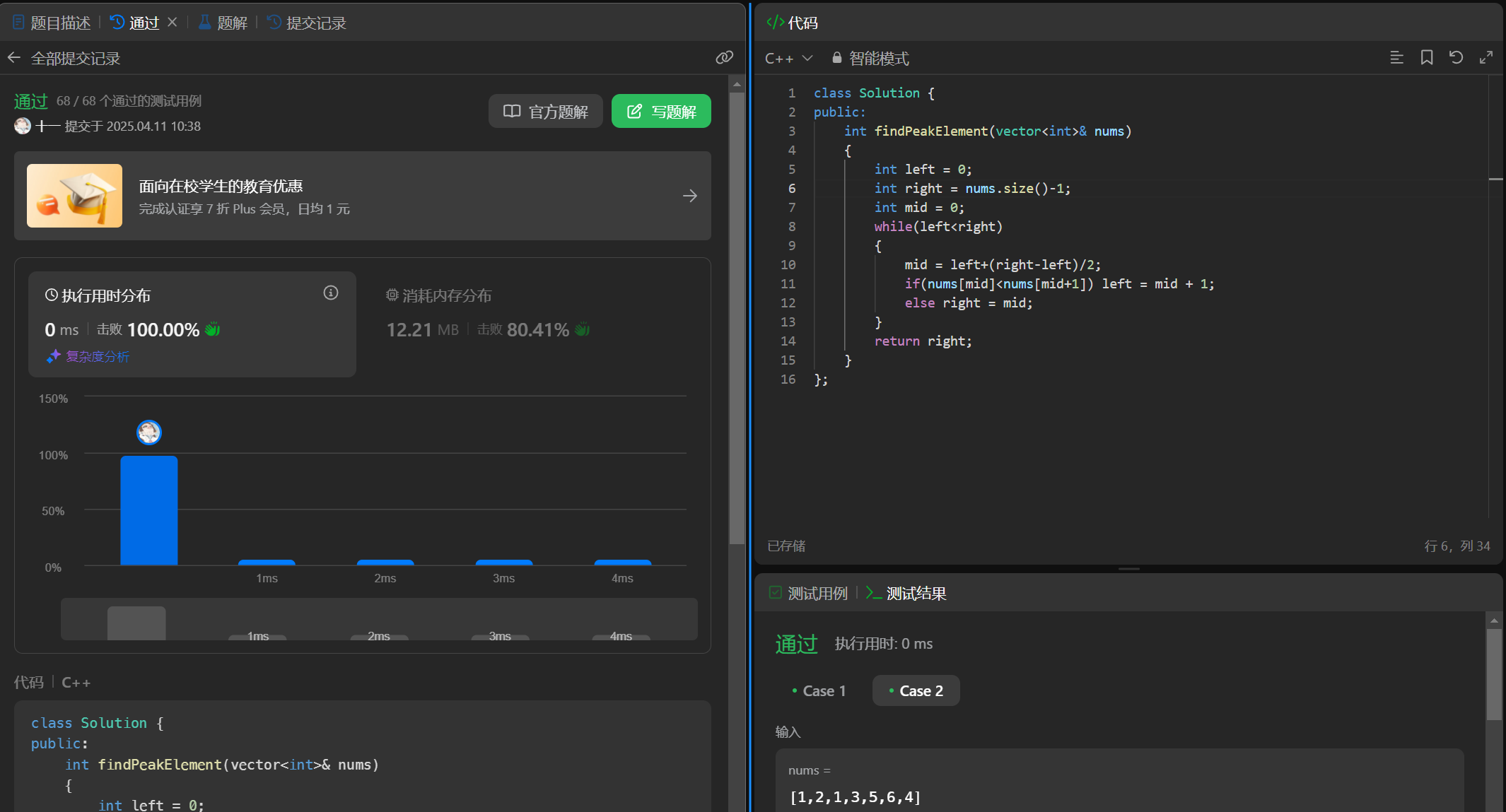
class Solution {
public:int findPeakElement(vector<int>& nums){int left = 0;int right = nums.size()-1;int mid = 0;while(left<right){mid = left+(right-left)/2;if(nums[mid]<nums[mid+1]) left = mid + 1;else right = mid;}return right;}
};

七、寻找旋转排序数组中最小的值

1、题目

https://leetcode.cn/problems/find-minimum-in-rotated-sorted-array/

2、解题思路

1、暴力查找：遍历整个数组，如果nums[i+1]<nums[i] ，i即为最小值的索引

2、二分算法：首先我们可以将这个数组给大致画出来

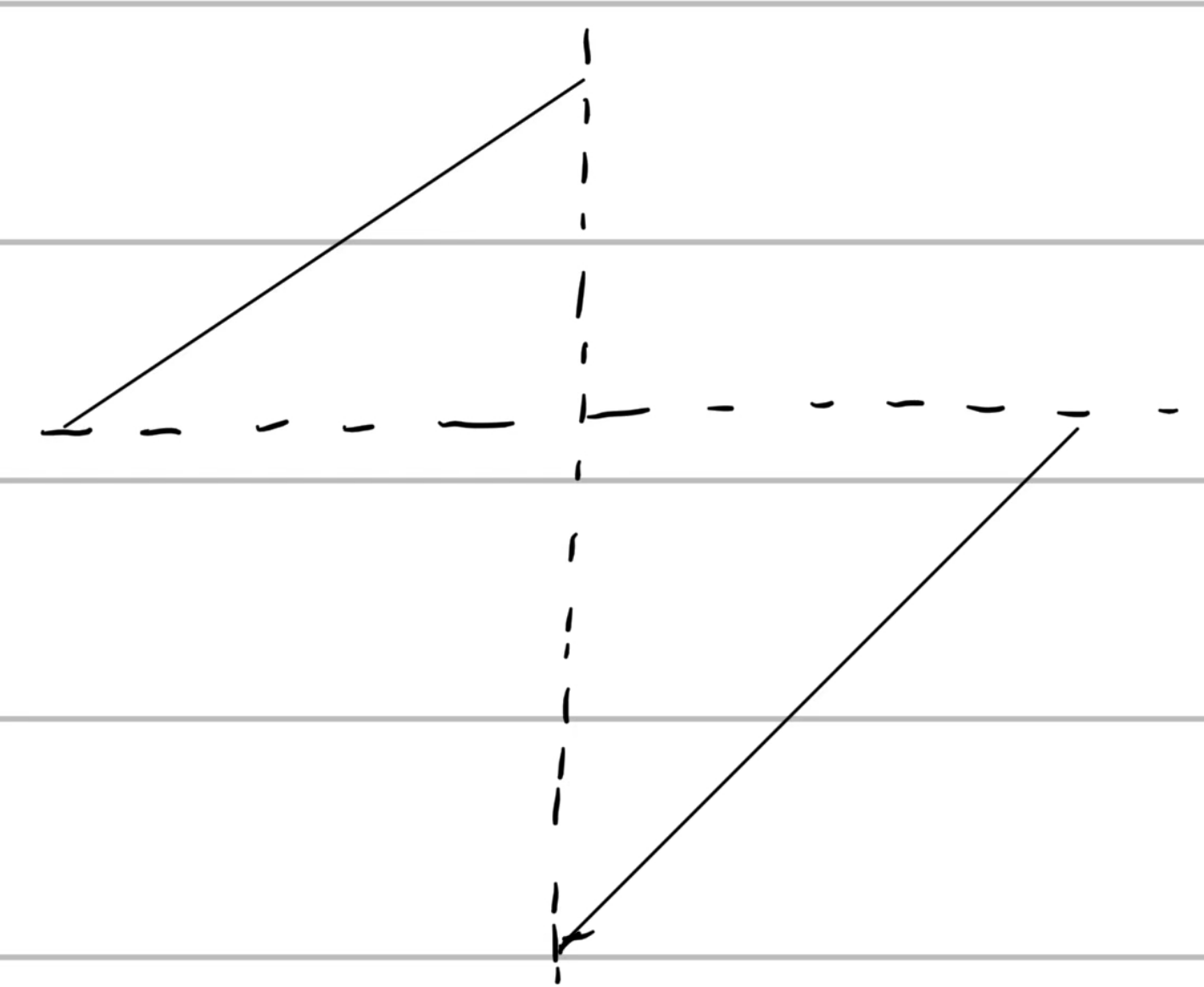
如上图，我们可以能明显的发现二分性，左边始终大于最后一个的值，右边始终小于等于最后一个值

我们定义left ，right 分别指向第一个值和最后一个值，当他们的中间值nums[mid] (mid = left +(right- left)/2)<= nums[nums.size()-1] right = mid; 当他们的中间值nums[mid] >nums[nums.size()-1] left= mid+1 ;

3、代码编写

class Solution {
public:int findMin(vector<int>& nums) {int left = 0;int right = nums.size()-1;int mid = 0;while(left<right){mid = left +(right -left)/2;if(nums[mid] <= nums[nums.size()-1])  right = mid;else  left = mid +1;}return nums[left];}
};

一、二分查找

1、题目

2、解题思路

3、代码实现

4、时间复杂度

5、朴素二分法的模板总结

二、在排序数组中查找元素的第一个和最后一个位置

1、题目

2、题目解析

3、代码实现

4、 模板总结（重点）

三、x的算法平方根

1、题目

2、 题目解析

3、代码实现

四、搜索插入位置

1、题目

2、题目解析

3、代码实现

五、上峰数组的索引

1、题目

2、题目解析

3、代码实现

六、寻找峰值

1、题目

2、解题思路

3、代码编写

相关文章：

4、模板总结（重点）

2、题目解析