机器学习课堂7用scikit-learn库训练SVM模型
1.用scikit-learn库训练SVM模型
代码
# 2-11用scikit-learn库训练SVM模型
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm # 导入sklearn# 参数设置
m_train = 250 # 训练样本数量
svm_C = 100 # SVM的C值
svm_kernel = 'linear' # SVM的核函数
# 读入酒驾检测数据集
df = pd.read_csv('alcohol_dataset.csv')
data = np.array(df)
m_all = np.shape(data)[0] # 样本总数
d = np.shape(data)[1] - 1 # 输入特征的维数
m_test = m_all - m_train # 测试数据集样本数量
# 把0标注替换为-1
data[:, d] = np.where(data[:, d] == 0, -1, data[:, d])
# 构造随机种子为指定值的随机数生成器,并对数据集中样本随机排序
rng = np.random.default_rng(1)
rng.shuffle(data)
mean = np.mean(data[0:m_train, 0:d], axis=0) # 计算训练样本输入特征的均值
std = np.std(data[0:m_train, 0:d], axis=0, ddof=1) # 计算训练样本输入特诊的标准差
data[:, 0:d] = (data[:, 0:d] - mean) / std # 标准化所有样本的输入特征
# 划分数据集
X_train = data[0:m_train, 0:d] # 训练集输入特征
X_test = data[m_train:, 0:d] # 测试集输入特征
Y_train = data[0:m_train, d] # 训练集目标值
Y_test = data[m_train:, d] # 测试集目标值
# SVM训练与预测
clf = svm.SVC(kernel=svm_kernel, C=svm_C)
clf.fit(X_train, Y_train) # 训练
Y_train_hat = clf.predict(X_train) # 训练数据集上的预测
Y_test_hat = clf.predict(X_test) # 测试数据集上的预测
# 打印分类错误的数量
print('Trainset prediction errors=', np.sum(Y_train != Y_train_hat))
print('Testset prediction errors=', np.sum(Y_test != Y_test_hat))
# 训练数据集上的混淆矩阵
tp = np.sum(np.logical_and(Y_train == 1, Y_train_hat == 1)) # TP
fp = np.sum(np.logical_and(Y_train == -1, Y_train_hat == 1)) # FP
tn = np.sum(np.logical_and(Y_train == -1, Y_train_hat == -1)) # TN
fn = np.sum(np.logical_and(Y_train == 1, Y_train_hat == -1)) # FN
print(f'Trainset TP={tp},FP={fp},TN={tn},FN={fn}')
# 训练数据集上的召回率、精度、F1值
recall = tp / (tp + fn)
precision = tp / (tp + fp)
f1 = 2 * recall * precision / (recall + precision)
print(f'Trainset recall={recall:.3},presision={precision:.3},F1={f1:.3}')
# 测试数据集上的混淆矩阵
tp_test = np.sum(np.logical_and(Y_test == 1, Y_test_hat == 1))
fp_test = np.sum(np.logical_and(Y_test == -1, Y_test_hat == 1))
tn_test = np.sum(np.logical_and(Y_test == -1, Y_test_hat == -1))
fn_test = np.sum(np.logical_and(Y_test == 1, Y_test_hat == -1))
print(f'Trestset TP={tp_test},FP={fp_test},TN={tn_test},FN={fn_test}')
# 测试数据集上的召回率、精度、F1值
recall_test = tp_test / (tp_test + fn_test)
precision_test = tp_test / (tp_test + fp_test)
f1_test = 2 * recall_test * precision_test / (recall_test + precision_test)
print(f'Trainset recall={recall_test:.3},presision={precision_test:.3},F1={f1_test:.3}')
结果
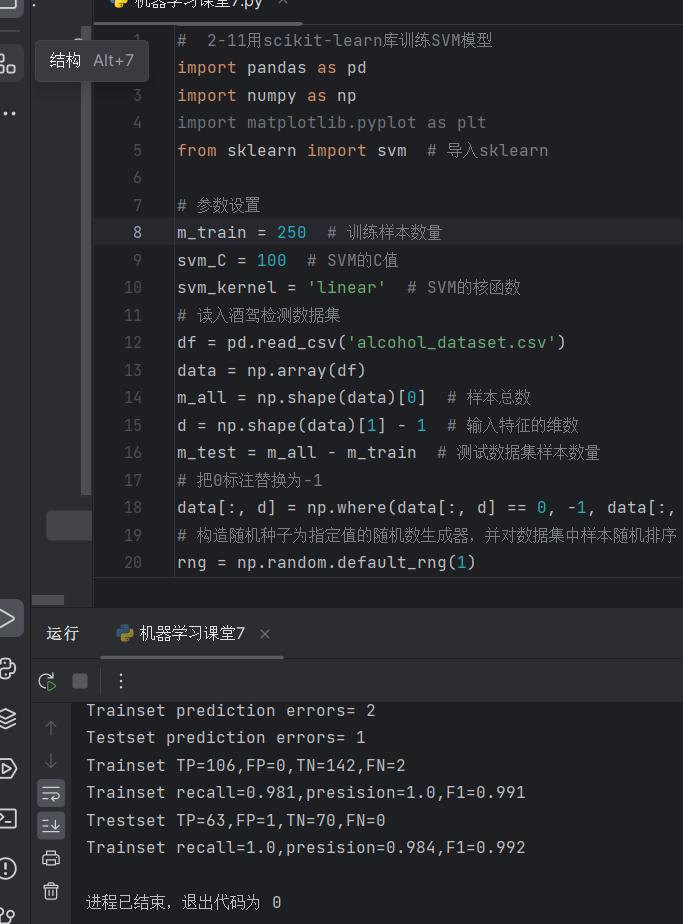
2.SVM模型的分类错误数量随C值变化的曲线
# 2-12画出SVM模型都分类错误数量随C值变化的曲线
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm # 导入sklearn# 参数设置
m_train = 250 # 训练样本数量
svm_kernel = 'poly' # SVM的核函数
points_C = 70 # SVM的C值取值数量
step_C = 0.1 # C值的步长
# 读入酒驾检测数据集
df = pd.read_csv('alcohol_dataset.csv')
data = np.array(df)
m_all = np.shape(data)[0] # 样本总数
d = np.shape(data)[1] - 1 # 输入特征的维数
m_test = m_all - m_train # 测试数据集样本数量
# 把0标注替换为-1
data[:, d] = np.where(data[:, d] == 0, -1, data[:, d])
# 构造随机种子为指定值的随机数生成器,并对数据集中样本随机排序
rng = np.random.default_rng(1)
rng.shuffle(data)
mean = np.mean(data[0:m_train, 0:d], axis=0) # 计算训练样本输入特征的均值
std = np.std(data[0:m_train, 0:d], axis=0, ddof=1) # 计算训练样本输入特诊的标准差
data[:, 0:d] = (data[:, 0:d] - mean) / std # 标准化所有样本的输入特征
# 划分数据集
X_train = data[0:m_train, 0:d] # m_train*d维
X_test = data[m_train:, 0:d] # m_test*d维
Y_train = data[0:m_train, d] # m_train*1维
Y_test = data[m_train:, d] # m_test*1维
# 用来保存两个数据集上的分类错误数量
train_errors = np.zeros(points_C)
test_errors = np.zeros(points_C)
# C循环
for c in range(points_C):# 当前C值svm_C = (c + 1) * step_C# SVM训练与预测clf = svm.SVC(kernel=svm_kernel, C=svm_C)clf.fit(X_train, Y_train) # 训练Y_train_hat = clf.predict(X_train) # 训练数据集上的预测Y_test_hat = clf.predict(X_test) # 测试数据集上的预测# 统计并保存两个数据集上的分类错误的数量train_errors[c] = np.sum(Y_train != Y_train_hat)test_errors[c] = np.sum(Y_test != Y_test_hat)
# 画出两条分类错误线
plt.plot(np.arange(1, points_C + 1) * step_C, train_errors, 'r-o', linewidth=2, markersize=5)
plt.plot(np.arange(1, points_C + 1) * step_C, test_errors, 'r-o', linewidth=2, markersize=5)
plt.ylabel('Number of errors')
plt.xlabel('C')
plt.legend(['Traininng dataset', 'Test dataset'])
plt.annotate('Underfitting', (0.3, 18), fontsize=12)
plt.annotate('Best fit', (2.5, 18), fontsize=12)
plt.annotate('Overfitting', (4.8, 18), fontsize=12)
plt.plot((0.9, 0.9), (-2, 15), '--k')
plt.plot((4.3, 4.3), (-2, 15), '--k')
plt.axis([0, 7, -2, 37])
plt.show()
结果图
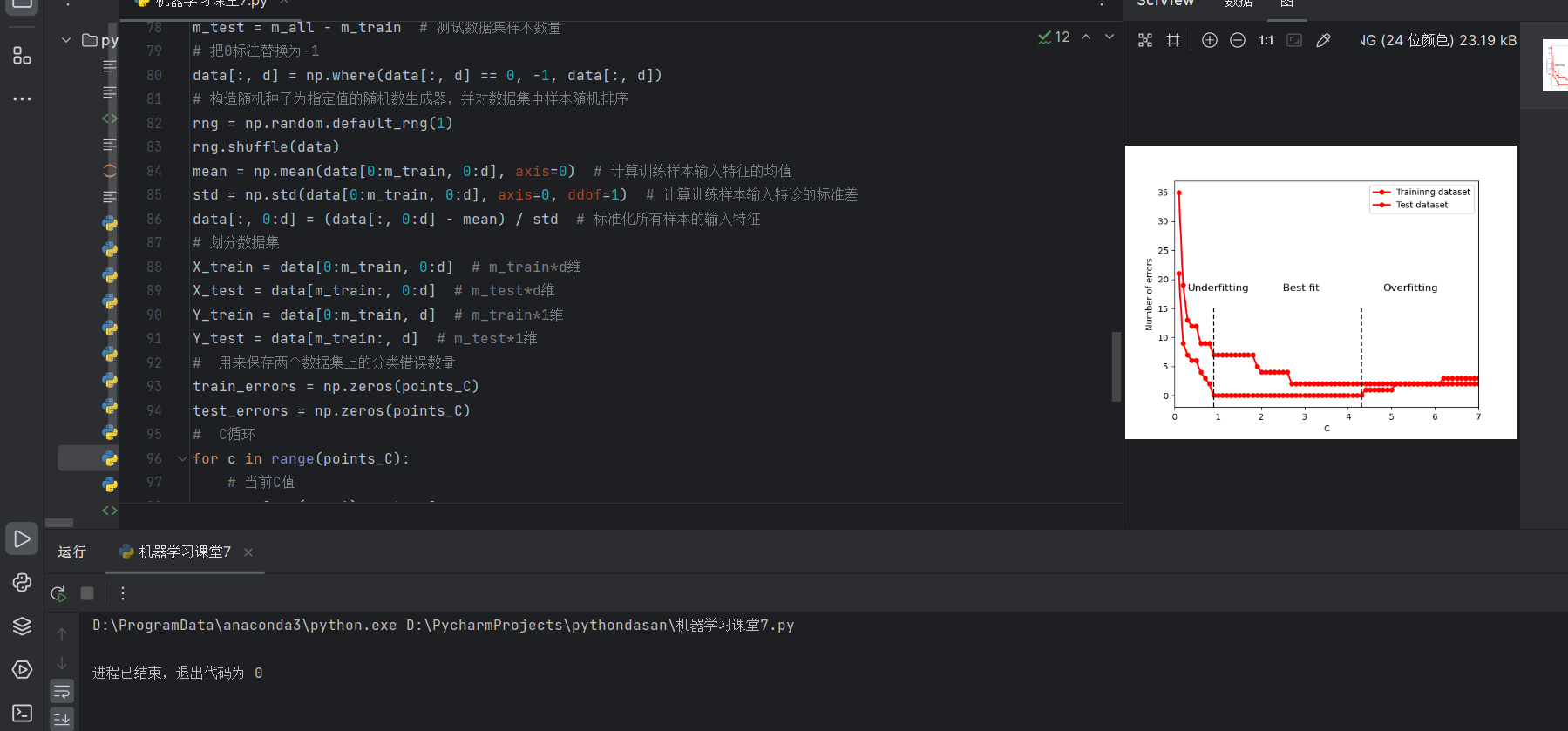
相关文章:

机器学习课堂7用scikit-learn库训练SVM模型
1.用scikit-learn库训练SVM模型 代码 # 2-11用scikit-learn库训练SVM模型 import pandas as pd import numpy as np import matplotlib.pyplot as plt from sklearn import svm # 导入sklearn# 参数设置 m_train 250 # 训练样本数量 svm_C 100 # SVM的C值 svm_kernel …...
)
模拟考试系统(ssm+vue+mysql5.x)
模拟考试系统(ssmvuemysql5.x) 模拟考试系统是一个为考试准备和管理提供全面支持的平台。系统提供了丰富的功能模块,包括个人中心、科目管理、复习资料管理、参考文献管理、用户管理、留言板管理、试题管理、试卷管理、系统管理和考试管理。用户可以在个人中心修改…...

【计网】作业4
一. 单选题(共22题,64分) 1. (单选题)主机甲采用停止-等待协议向主机乙发送数据,数据传输速率是4kb/s,单向传播时延为30ms,忽略确认帧的发送时延。当信道利用率等于80%时,数据帧的长度为&#…...

MYSQL数据库语法补充
一,DQL基础查询 DQL(Data Query Language)数据查询语言,可以单表查询,也可以多表查询 语法: select 查询结果 from 表名 where 条件; 特点: 查询结果可以是:表中的字段…...

Java基础编程练习第38题-除法器
题目:编写一个除法器,输入被除数和除数,并将结果输出。 这道题看似很简单,实则也不难。 就是假如用户输入的类型不同怎么办呢?用户输入int或者double类型应该怎么解决。这里我们就需要用到函数的重载。 代码如下&am…...

【基于Vue3组合式API的互斥输入模式实现与实践分享】
基于Vue3组合式API的互斥输入模式实现与实践分享 目录 背景与痛点设计思路技术实现使用场景与案例遇到的问题与解决方案最佳实践总结 1. 背景与痛点 在表单交互设计中,我们经常面临这样的场景:多种输入方式互斥。例如,在评分系统中&#…...

Linux进程概念及理解
目录 冯诺依曼体系结构 操作系统(Operator System) 概念 设计OS的目的 定位 如何理解 "管理" 总结 系统调用和库函数概念 进程 基本概念 描述进程-PCB task_struct-PCB的一种 task_ struct内容分类 组织进程 查看进程 通过系统调用获取进程标示符 通过系统调用创建进…...

苹果签名是否安全
苹果开发者与运营商都对苹果签名有一定了解,那么苹果签名安全吗?下面我来跟大家聊一聊。 苹果签名能验证应用的来源,但存在一些风险,有开发者伪造签名,让用户认为此产品是可信的,这样就安装到了恶意应用&am…...
环境下,需要手动实现队列机制来替代FreeRTOS的CAN发送接收函数)
STM32在裸机(无RTOS)环境下,需要手动实现队列机制来替代FreeRTOS的CAN发送接收函数
xQueueSendToBackFromISR(ecuCanRxQueue, hcan->pRxMsg, &xHigherPriorityTaskWoken),xQueueReceive(mscCanRxQueue,&mscRxMsg,0)和xQueueSendToBack(mscCanTxQueue, &TxMessageTemp, 0 )这3个函数,在裸机下实现: 在裸机&…...

无法看到新安装的 JDK 17
在 Linux 系统中使用 update-alternatives --config java 无法看到新安装的 JDK 17,可能是由于 JDK 未正确注册到系统备选列表中。 一、原因分析 JDK 未注册到 update-alternatives update-alternatives 工具需要手动注册 JDK 路径后才能识别新版本。如果仅安装 JDK…...

JavaEE——线程的状态
目录 前言1. NEW2. TERMINATED3. RUNNABLE4. 三种阻塞状态总结 前言 本篇文章来讲解线程的几种状态。在Java中,线程的状态是一个枚举类型,Thread.State。其中一共分为了六个状态。分别为:NEW,RUNNABLE,BLOCKED,WAITING,TIMED_WAITING, TERMI…...
)
数据结构与算法-数学-(同余,线性同余方程,中国剩余定理,卡特兰数,斯特林数)
同余方程: 1.1 线性同余方程 & 乘法逆元 线性同余方程是形如 ax≡b(mod m) 的方程,可转化为 axmyb 的线性不定方程,利用扩展欧几里得算法求解。当 b1 时,x 就是 a 在模 m 意义下的乘法逆元。 代码: #include &…...

RAG 系统中的偏差是什么?
检索增强生成 (RAG) 在减少模型幻觉和增强大型语言模型 (LLM)的领域特定知识库方面已获得广泛认可。通过外部数据源佐证大型语言模型生成的信息,有助于保持模型输出的新鲜度和真实性。然而,最近在 RAG系统中的发现,突显了基于 RAG 的大型语言…...

[创业之路-362]:用确定性的团队、组织、产品开发流程和方法,应对客户、市场、竞争和商业模式的不确定性。
在充满不确定性的商业环境中,通过确定性的团队、组织、产品开发流程和方法构建核心竞争力,是应对客户、市场、竞争和商业模式变化的核心策略。以下从团队韧性、组织敏捷、产品开发闭环三个维度,结合实战方法论,提供可落地的解决方…...
)
系统与网络安全------网络通信原理(1)
资料整理于网络资料、书本资料、AI,仅供个人学习参考。 文章目录 网络通信模型协议分层计算机网络发展计算机网络功能什么是协议为什么分层邮局实例 OSI模型OSI协议模型OSI七层模型OSI七层的功能简介 TCP/IP模型OSI模型与TCP/IP模型TCP/IP协议族的组成各层PDU设备与…...

ArkTS语言基础之函数
前言 臭宝们终于来到了ArkTS基础之函数,今天我们来学习一下ArkTS的函数的相关知识,上一节中也有一些函数的基础知识。 函数声明 函数声明引入一个函数,包含其名称、参数列表、返回类型和函数体,在下面的例子中,我们声明了一个名…...

synchronized锁升级的锁对象和Mark Word
在讨论synchronized锁升级和Mark Word时,提到的"对象"通常指的是锁对象,也就是被用作synchronized同步锁的那个Java对象。 1. 什么是锁对象? 锁对象是指被用于synchronized同步代码块或方法的对象实例。例如: // 这个…...
插入排序 希尔排序 冒泡排序)
数据结构|排序算法(二)插入排序 希尔排序 冒泡排序
一、插入排序 1.算法思想 插入排序(Insertion Sort)是一种简单的排序算法,其基本思想是:将待排序的元素插入到已经有序的序列中,从而逐步构建有序序列。 具体过程如下: 把待排序的数组分为已排序和未排…...

12、主频和时钟配置实验
一、I.MX6U 时钟系统详解 1、系统时钟来源 开发板的系统时钟来源于两部分: 32.768KHz 和24MHz 的晶振,其中 32.768KHz 晶振是 I.MX6U 的 RTC 时钟源, 24MHz 晶振是 I.MX6U 内核和其它外设的时钟源。 2、7路PLL时钟源 I.MX6U 的外设有很多,不同的外设时钟源不同, NXP 将…...

DFS和BFS的模版
dfs dfs金典例题理解就是走迷宫 P1605 迷宫 - 洛谷 dfs本质上在套一个模版: ///dfs #include<bits/stdc.h> using namespace std; int a[10][10]{0}; int m,n,t,ans0; int ex,ey; int v[10][10]{0}; int dx[4]{-1,0,1,0}; int dy[4]{0,1,0,-1}; void dfs(in…...

docker镜像导出导入
在Docker中,可以很容易地导出和导入镜像,这对于备份、迁移或者在不同的环境中共享镜像非常有用。以下是操作步骤: 导出镜像 使用 docker save docker save 命令可以用来将一个或多个镜像保存到一个文件中,这个文件可以被导入到任…...

大模型Agent | 构建智能体 AI-Agent的 5大挑战,及解决方案!
源自: AINLPer(每日干货分享!!) 编辑: ShuYini 校稿: ShuYini 时间: 2025-4-7 更多:>>>>专注大模型/AIGC、学术前沿的知识分享! 引言 AI-Agent正变得越来越智能,它能够根据用户需…...

基于STM32、HAL库的IP2721 快充协议芯片简介及驱动程序设计
一、简介: IP2721是一款高性能的USB PD (Power Delivery)协议控制器芯片,主要用于USB Type-C接口的电源管理。它支持USB PD 3.0规范,能够实现多种电压和电流的协商,广泛应用于充电器、移动电源等设备。 主要特性: 支持USB PD 3.0规范 支持Type-C接口的DRP/SRC/SNK模式 内…...

荣耀90 GT信息
外观设计 屏幕:采用 6.7 英寸 AMOLED 荣耀绿洲护眼屏,超窄边框设计,其上边框 1.6mm,左右黑边 1.25mm,屏占较高,带来更广阔的视觉体验。屏幕还支持 120Hz 自由刷新率,可根据使用场景自动切换刷新…...

53. 评论日记
要自己有判断是非的能力宝子们。#小米 #小米su7 #雷军 #神操作 #小米su7ultra_哔哩哔哩_bilibili 2025年4月8日19:30:57...
之安装Dashboard和CoreDNS)
【10】搭建k8s集群系列(二进制部署)之安装Dashboard和CoreDNS
一、部署Dashboard 1.1、创建kubernetes-dashboard.yaml文件 完整的yaml配置文件信息如下: # Copyright 2017 The Kubernetes Authors. # # Licensed under the Apache License, Version 2.0 (the "License"); # you may not use this file except in …...

【算法手记12】DP25 删除相邻数字的最大分数
🦄个人主页:修修修也 🎏所属专栏:刷题 ⚙️操作环境:牛客网 目录 一.DP25 删除相邻数字的最大分数 题目详情: 题目思路: 解题代码: 结语 一.DP25 删除相邻数字的最大分数 牛客网题目链接(点击即可跳转):DP25 删除相邻数字的最大分数 题目详情: 本题详情如…...

[Godot] C#简单实现人物的控制和动画
目录 实现效果 场景搭建 脚本实现 移动 动画 完整脚本 相机跟随 总结 实现效果 场景搭建 本文章只分享了关于移动和动画的,没有给碰撞体,大家根据需要自行添加吧 相机的缩放大小可以根据自己的需要调整 我的人物动画结构是这样的,待机动…...

选择站群服务器租用的优势都有什么?
站群服务器是一种专门用于托管多个网站的服务器,是通过集中管理和资源分配,可以支持同时运行数十个甚至是数百个独立网站,站群服务器的主要特点就是让每个网站可以分配独立的IP地址,避免出现IP关联风险,通过统一控制面…...

VS Code下开发FPGA——FPGA开发体验提升__下
上一篇:IntelliJ IDEA下开发FPGA-CSDN博客 Type:Quartus 一、安装插件 在应用商店先安装Digtal IDE插件 安装后,把其他相关的Verilog插件禁用,避免可能的冲突。重启后,可能会弹出下面提示 这是插件默认要求的工具链&a…...

leetcode13.罗马数字转整数
遍历,下一个值不大于当前值就加上当前值,否则就减去当前值 class Solution {public int romanToInt(String s) {Map<Character, Integer> map Map.of(I, 1,V, 5,X, 10,L, 50,C, 100,D, 500,M, 1000);int sum 0;for (int i 0; i < s.length(…...

WVP-PRO配置与部署
ZLMediaKit部署与配置 https://blog.csdn.net/qq_38179971/article/details/147043763MySQL8.0.13安装[Ubuntu16.04] cd /usr/local/src wget http://soft.vpser.net/lnmp/lnmp1.6.tar.gz -cO lnmp1.6.tar.gz && tar zxf lnmp1.6.tar.gz && cd lnmp1.6 &…...

opencv图像库编程
目录 一、Linux搭建C OpenCV开发环境1.安装必要依赖项2.安装opencv3、cmake分析4、验证安装 二、编写一个打开图片进行特效显示的代码 test.cpp1.gcc方式编译1)在opencv3.4.5下新建mytest文件夹2)创建test.cpp3)编译 2.makemakefile方式编译3…...

【Easylive】定时任务-每日数据统计和临时文件清理
【Easylive】项目常见问题解答(自用&持续更新中…) 汇总版 这个定时任务系统主要包含两个核心功能:每日数据统计和临时文件清理。下面我将详细解析这两个定时任务的实现逻辑和技术要点: Component Slf4j public class SysTas…...

搜广推校招面经七十
美团暑期推荐实习 一、讲一下self-attention,qkv的含义。 见【搜广推校招面经五】 二、讲一下协同过滤召回,新闻推荐项目为什么不用usercf? 见【搜广推校招号面经六十四】 三、介绍信息增益公式(Information Gain) 见【搜广…...

TypeScript 泛型详解及应用场景
泛型(Generics)是 TypeScript 的核心特性,它允许我们编写可复用、类型安全的代码,同时保持灵活性。以下是深度解析和实际应用指南: 一、泛型基础概念 本质:参数化类型,将类型作为变量传递&…...
2017)
Proximal Policy Optimization (PPO)2017
2.1 策略梯度方法 策略梯度方法计算策略梯度的估计值并将其插入到随机梯度上升算法中。最常用的梯度估计器的形式如下: g ^ E t [ ∇ θ log π θ ( a t ∣ s t ) A ^ t ] (1) \hat{g} \mathbb{E}_t \left[ \nabla_{\theta} \log \pi_{\theta}(a_t | s_t) \h…...
)
使用 Google ML Kit 实现图片文字识别(提取美国驾照信息)
Google ML Kit 是一个现代、功能强大、跨平台的机器学习 SDK。在这篇文章中,我们将使用 ML Kit 在 Android 应用中识别图片文字,以提取美国驾照上的关键信息:DL(驾照号) 和 EXP(有效日期)。 &am…...

VR体验馆如何用小程序高效引流?3步打造线上预约+团购裂变系统
VR体验馆如何用小程序高效引流?3步打造线上预约团购裂变系统 一、线上预约的核心价值:优化体验,提升转化 减少客户等待时间 通过小程序预约功能,客户可提前选择体验时段,避免到店排队。数据显示&#…...
)
前端知识(vue3)
1.Vue3 1.1 介绍 Vue(读音 /vjuː/, 类似于 view)是一款用于构建用户界面的渐进式的JavaScript框架 官网:https://cn.vuejs.org 1.2 常见指令 指令:指的是HTML 标签上带有 v- 前缀的特殊属性,不同指令具有不同含义…...

nginx 代理 https 接口
代码中需要真实访问的接口是:https://sdk2.028lk.com/application-localizationdev.yml文件中配置: url: http:/111.34.80.138:18100/sdk2.028lk.com/该服务器111.34.80.138上 18100端口监听,配置信息为: location /sdk2.028lk.c…...

网络带宽测速工具选择指南iperf3 nttcp tcpburn jperf使用详解
简介 本文主要介绍内网(局域网)与外网(互联网)的网络带宽测速工具下载地址、选择指南、参数对比、基本使用。 测速工具快速选择指南 测速工具下载地址 iperf 官网下载链接:iperf.fr/iperf-download.php该链接提供了不…...

解决TF-IDF增量学习问题的思路与方案
TF-IDF的传统实现面临增量学习困难,因为IDF计算依赖全局文档统计信息。但是实际的工作当中往往数据是增量的,并且定期增量和不定期增量混合,所以为了实际考虑,还是有必要思考如何解决TF-IDF增量问题的。 一、增量学习核心挑战 ID…...

【亲测】Linux 使用 Matplotlib 显示中文
文章目录 安装中文字体在Matplotlib中使用该字体来显示中文 在 Linux 系统中使用 Matplotlib 绘制图表时,如果需要显示中文,可能会遇到中文字符显示为方块或者乱码的问题。这是因为Matplotlib 默认使用的字体不支持中文。本文手把手带你解决这个问题。 …...

git clone阻塞问题
问题描述 git clone采用的ssh协议,在克隆仓库的时候,会经常卡一下,亦或是直接卡死不动。 最开始以为是公司电脑配置的问题,想着自己实在解决不了找it帮忙。 查阅资料发现,最终发现是git版本的问题,这个是…...

Json快速入门
引言 Jsoncpp 库主要是用于实现 Json 格式数据的序列化和反序列化,它实现了将多个数据对象组织成 为Json格式字符串,以及将 Json 格式字符串解析得到多个数据对象的功能,独立于开发语言。 Json数据对象 Json数据对象类的表示: …...

【QT】学习笔记1
QT概述 Qt是一个1991年由QtCompany开发的跨平台C图形用户界面应用程序开发框架。它既可以开发GUI程序,也可用于开发非GUI程序,比如控制台工具和服务器。Qt是面向对象的框架,使用特殊的代码生成扩展(称为元对象编译器(…...

【Kafka基础】生产者命令行操作指南:从基础到高级配置
Kafka作为分布式消息系统,其生产者是数据管道的起点。掌握kafka-console-producer.sh工具的使用对于开发测试和运维都至关重要。本文将系统介绍该工具的各种用法,帮助您高效地向Kafka发送消息。 1 基础消息生产 1.1 最简单的消息发送 /export/home/kafk…...

【Java面试系列】Spring Boot中自动配置原理与自定义Starter开发实践详解 - 3-5年Java开发必备知识
【Java面试系列】Spring Boot中自动配置原理与自定义Starter开发实践详解 - 3-5年Java开发必备知识 引言 Spring Boot作为Java生态中最流行的框架之一,其自动配置机制和Starter开发是面试中的高频考点。对于3-5年经验的Java开发者来说,深入理解这些原理…...
)
reid查找余弦相似度计算修正(二)
上一篇文章 reid查找余弦相似度计算(一) 上一篇的遗留问题就是reid 的结果部分正确,我们参考一下 fast-reid的demo,把里面的抽取特征提取出来 修改提取特征 首先发现图像改变大小的不同,fast 使用的是[128,384], 如…...
