当前位置： 首页 > news >正文

hot100_part_堆

news 来源：原创 2025/8/13 0:46:01

不该要求事情一开始就是完美。

堆排序

【从堆的定义到优先队列、堆排序】 10分钟看懂必考的数据结构——堆_哔哩哔哩_bilibili

排序算法：堆排序【图解+代码】_哔哩哔哩_bilibili

堆定义

        堆必须是完全二叉树，从上到下，从左到右不能用空缺。

        大根堆：每个父节点元素要大于它的子节点元素；小根堆同理

存储

        由于堆是完全二叉树，因此堆存放在数组中（树从上到下，从左到右依次存放到数组中）；

        根据完全二叉树父子下标节点的关系，如果当前节点的下标为 i ，那么其左子节点的下标为 2i+1，右子节点的下标为 2i+2。（树和数组的下标都是从0开始）

相关操作

以大顶堆为例

维护堆的性质（大顶堆为例），大顶堆对应下沉操作

arr：堆数组

n：数组长度

i：当前维护的元素下标

void heapify(int[] arr, int n, int i){int largest = i;int lson = i * 2 + 1;int rson = i * 2 + 2;if(lson < n && arr[largest] < arr[lson])largest = lson;if(rson < n && arr[largest] < arr[rson])largest = rson;if(largest != i){swap(arr[largest], arr[i]);heapify(arr, n, largest);}
}

建堆：

        根据节点下标之间的性质，下标为 i 的节点的父节点下标是：（i - 1）/ 2 ，由此可以得出堆中最后一个节点的父节点下标 x = （n-1 -1）/ 2  = n / 2 - 1 ，也是需要维护堆的性质的最后一个节点的下标。从x节点往前遍历调用heapify函数到0节点，就是一个建堆的过程。heapify是递归的函数。

        想一下建堆为什么是从底向上扫描而不是从顶向下扫描？

        因为要把更大的元素向上托举，从底向上能够遍历完所有的元素，自顶向下太局限，如果先维护根节点，就涉及两层，怎么保证根是最大

 堆排序：

        将堆顶元素和堆中最后一个元素交换，然后删除最后一个元素，重新维护堆顶元素的堆序性。每次的堆顶元素都是剩余元素中的最值。

void heap_sort(int[] arr, int n)
{int i ;//建堆for (i = n/2 - 1; i >= 0; i--)heapify(arr, n, i);//排序for(i = n - 1; i > 0; i--){swap(arr[i], arr[0]);heapify(arr, i, 0);}}

 建堆的时间复杂度为O(N)，heapify的复杂度为O(logN)，堆排序的复杂度O(NlogN)

快速排序

快速排序(QuickSort）算法介绍_快速排序算法-CSDN博客

        这些都是基础内容了，可见自己的基础知识很不扎实。

        快速排序的总体思想就是每趟遍历确定一个元素的最终位置。如果一个元素前面都是小于它的元素，后面都是大于它的元素，那么它的最终位置肯定也是在这个地方了。     

       选择数组要排序部分的第一个数作为基准数，并在要排序部分的首尾设置两个哨兵，向中间遍历；头部哨兵走到大于基准的位置停止，尾部哨兵走到小于基准的位置停止，交换彼此执向的数，直到两者相遇；这样就保证头指针走过的位置是小于基准的，尾指针走过的位置是大于基准的。

        结合分治的思想，最终使整个数组有序。这总体的代码写法很类似于树的先序遍历。

        注意，这个思想和二分查找的也有相似的地方，就是说，最后相遇的下标，还要和基准值进行交换，如果我们选择第一个元素作为基准值，这个也是最后要交换的位置index，那么要和基准值进行交换的元素一定是小于等于基准值的，因为index在左半边。所以移动指针时要先移动右半元素，使得right向left靠近，停在第一个小于等于基准的地方进行交换。

        上面这段话没看懂，为什么和right交换，直接举例子自己动手试一下

题目

这个就三题

215.数组中的第K个最大元素

        仔细读题，要求返回数组排序之后的倒数第 k 个位置，而不是第k大的元素。一般来说，直接排序后从尾部返回。笑死了，直接下标返回就行，看自己写的还是一个个返回真笑死。

        下面这两个在算法第四版都学过的。。。都忘完了

快速排序

while循环结束时，ij相等，指向的位置就是基准值的位置

堆排序

力扣很贴心，提醒这是面试常考。但是堆排序还是不满足O(n)的时间复杂度啊。按照上面的模板去写。问题出在了swap函数，这是很基础的东西，你写的时候直接交换了两个形参，真是傻逼，要把数组也传过去交换数组元素。

java实现swap函数的几种方案_java swap-CSDN博客

347.前K个高频元素

295.数据流的中位数

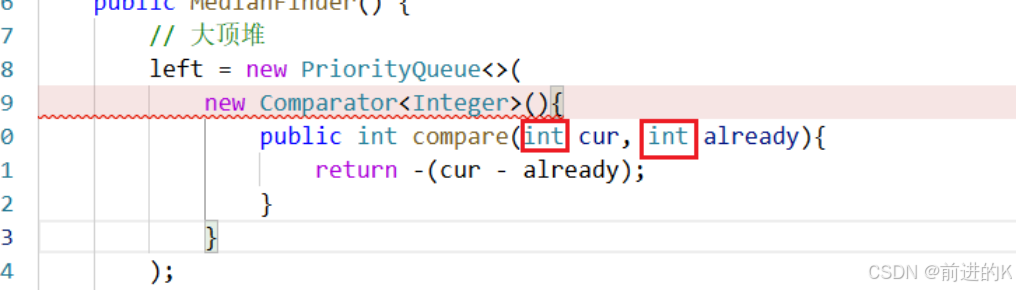
维护

right的最小一定比left的最大大，长度关系相等或者left多一个

相关文章：

hot100_part_堆

不该要求事情一开始就是完美。 堆排序 【从堆的定义到优先队列、堆排序】 10分钟看懂必考的数据结构——堆_哔哩哔哩_bilibili 排序算法&#xff1a;堆排序【图解代码】_哔哩哔哩_bilibili 堆定义 堆必须是完全二叉树&#xff0c;从上到下&#xff0c;从左到右不能用空缺。…...

编程日记 2025/8/13 0:46:01

CoreData 调试警告：多个 NSEntityDescriptions 声明冲突的解决

概述 目前在苹果生态 App 的开发中&#xff0c;CoreData 数据库仍然是大部分中小应用的优先之选。不过&#xff0c;运行时 CoreData 常常产生各种“絮絮叨叨”的警告不禁让初学的秃头小码农们云里雾里。 这不&#xff0c;对于下面这一大段 CoreData 警告&#xff0c;大家是否一…...

编程日记 2025/8/9 13:56:37

【白话神经网络（二）】矩阵、CNN、RNN

全连接层 回顾前面学过的知识&#xff1a; 一个最简单的神经网络&#xff0c;就是ywxb 套上一个激活函数。 如果有多个输入&#xff0c;那就是多个w和x 如果有多个输出&#xff0c;那就再来一行公式&#xff0c;多一组w和b 要是神经元多了的话&#xff0c;公式密密麻麻的&…...

编程日记 2025/8/12 18:14:57

map容器练习：使用map容器识别统计单词个数

题目链接&#xff1a;单词识别_牛客题霸_牛客网 对map的使用不太熟悉的同学可以参考&#xff1a;超详细介绍map&#xff08;multimap&#xff09;的使用-CSDN博客 题目解析 输入一个英文句子&#xff0c;把句子中的单词(不区分大小写)按出现次数按从多到少把单词和次数在屏幕…...

编程日记 2025/8/11 5:18:32

DeepSeek 是否被过度吹捧了？

DeepSeek 作为中国人工智能领域的后起之秀&#xff0c;其技术进展引发了广泛关注和讨论。然而&#xff0c;DeepSeek 是否被过度吹捧仍然值得客观分析。 DeepSeek 的确取得了不错的成果&#xff0c;不过可能没有媒体宣传和人们想象中那么重大。它的轰动性主要在于以低廉的成本达…...

编程日记 2025/8/11 20:32:37

前端大文件上传（分片上传）与下载

文章目录 一、问题二、思路1、选择文件2、校验文件是否符合规范3、文件切片上传4、分片上传注意点5、大文件下载 一、问题 日常业务中难免出现前端需要向后端传输大型文件的情况&#xff0c;这时单次的请求不能满足传输大文件的需求&#xff0c;就需要用到分片上传 业务需求为…...

编程日记 2025/8/6 16:54:17

【最佳实践】Go 状态模式

设计思路 状态模式的核心在于将对象的行为封装在特定的状态类中&#xff0c;使得对象在不同的状态下表现出不同的行为。每个状态实现同一个接口&#xff0c;允许对象在运行时通过改变其内部状态对象来改变其行为。状态模式使得状态转换更加明确&#xff0c;并且易于扩展新的状…...

编程日记 2025/8/5 1:13:08

如何用Python批量将CSV文件编码转换为UTF-8并转为Excel格式？

在处理数据时&#xff0c;CSV文件格式常常用作数据的交换格式。不过&#xff0c;很多情况下我们会遇到编码问题&#xff0c;特别是当文件不是UTF-8编码时。为了更好地处理这些文件&#xff0c;可能需要将它们转换为UTF-8编码&#xff0c;并且将其转换为Excel格式&#xff0c;这…...

编程日记 2025/8/2 19:19:01

回顾Transformer，并深入讲解替代方案Mamba原理(图解)

一种语言建模中 Transformer 的替代方案 Transformer 架构是大语言模型&#xff08;LLMs&#xff09;成功的关键组成部分。几乎所有今天使用的大语言模型都采用了该架构&#xff0c;从开源模型如 Mistral 到闭源模型如 ChatGPT。 为了进一步改进大语言模型&#xff0c;新的架构…...

编程日记 2025/8/6 4:58:58

2025开源风险治理最佳实践︱新能源汽车车企开源风险治理案例

案例来源&#xff1a;悬镜安全 案例背景 当前我国新能源汽车产业蓬勃发展&#xff0c;智能网联趋势持续深化。汽车技术与工程核心逐渐从传统硬件层面转移到软件层面&#xff0c;踏上软件定义汽车(SDV)的变革之路。引用开源组件成为车企、Tier1、Tier2在软件开发过程中的常规操…...

编程日记 2025/8/9 22:22:19

Spring中Bean的自动装配

1.自动装配的核心概念 定义&#xff1a; Bean的自动装配是Spring框架中用于自动满足Bean依赖的一种机制。通过自动装配&#xff0c;Spring容器会在应用上下文中为某个Bean寻找其依赖的Bean&#xff0c;从而减少手动配置的工作量。其核心目标是减少配置代码&#xff0c;通过类型…...

编程日记 2025/8/11 8:25:15

一文掌握 PostgreSQL 的各种指令（PostgreSQL指令备忘）

引言 PostgreSQL 作为一款功能强大、开源的关系型数据库管理系统&#xff08;RDBMS&#xff09;&#xff0c;以其高扩展性、SQL 标准兼容性以及丰富的功能特性&#xff0c;成为企业级应用的首选数据库之一。无论是开发、运维还是数据分析&#xff0c;掌握 PostgreSQL 的核心指…...

编程日记 2025/8/13 0:41:38

C#入门学习记录（三）C#中的隐式和显示转换

C#类型转换&#xff1a;隐式与显式转换的机制与应用 在C#的强类型体系中&#xff0c;数据类型转换是实现数据交互和算法逻辑的基础操作。当数值类型范围存在包含关系&#xff0c;或对象类型存在继承层次时&#xff0c;系统通过预定义的转换规则实现类型兼容处理。隐式转换&…...

编程日记 2025/8/7 21:31:08

【Linux网络-网络层】TCP与IP的关系+IP协议基本概念+网段划分+路由+IP分片与组装

网络层 在复杂的网络环境中确定一个合适的路径 一、TCP与IP的关系 TCP&#xff08;传输控制协议&#xff09;和IP&#xff08;互联网协议&#xff09;是互联网协议栈中的两个核心协议&#xff0c;属于不同的层级&#xff0c;分别在传输层和网络层&#xff0c;共同实现数据的可…...

编程日记 2025/8/11 22:57:53

【第K小数——可持久化权值线段树】

题目 代码 #include <bits/stdc.h> using namespace std;const int N 1e5 10;int a[N], b[N]; int n, m, len; int rt[N], idx; // idx 是点分配器struct node {int l, r;int s; } tr[N * 22];int getw(int x) {return lower_bound(b 1, b len 1, x) - b; }int bui…...

编程日记 2025/8/7 10:54:41

需要使用新应用以打开此ms-gamingoverlay链接怎么解决

要解决Windows系统提示“需要使用新应用以打开此ms-gamingoverlay链接”的问题&#xff0c;通常与系统自带的游戏工具栏&#xff08;Game Bar&#xff09;或Xbox相关应用缺失或配置错误有关。以下是综合多个来源的详细解决方法&#xff1a; 方法1&#xff1a;关闭游戏栏功能 这…...

编程日记 2025/7/30 10:22:18

五子棋小游戏-简单开发版

一、需求分析 开发一个基于 Pygame 库的五子棋小游戏&#xff0c;允许两名玩家在棋盘上轮流落子&#xff0c;当有一方达成五子连珠时游戏结束&#xff0c;显示获胜信息&#xff0c;并提供退出游戏和重新开始游戏的操作选项。 1.棋盘显示 &#xff1a; 显示一个 15x15 的五子棋…...

编程日记 2025/8/13 0:44:59

C语言内存函数讲解

&#xff08;一&#xff09;memcpy函数 这是memcpy函数的说明。它的头文件是string.h。函数原型是 void* memcpy(void* destination, const void* source, size_t num) 第一个参数是一个指向一个字符串的指针&#xff0c;第二个也是一样的。而第三个参数是复制的字节个数。这…...

编程日记 2025/8/11 17:25:57

2018年全国职业院校技能大赛高职组-计算机网络应用竞赛竞赛样题C卷

目录 总体规划 模块二：设备基础信息配置 模块三：网络搭建与网络冗余备份方案部署 模块四：移动互联网搭建与网优 模块五：出口安全防护与远程接入 总体规划 CII教育公司在进行企业大学信息化建设的过程中，为了保证北京校区、广州校区与本部校区的日常OA办公通信等关键业务，…...

编程日记 2025/8/10 15:04:25

《解锁Flutter：跨平台开发的未来之光》：此文为AI自动生成

《解锁Flutter&#xff1a;跨平台开发的未来之光》&#xff1a;此文为AI自动生成 Flutter&#xff1a;崭新时代的跨平台框架 在当今数字化浪潮中&#xff0c;移动应用已成为人们生活中不可或缺的一部分。无论是购物、社交、娱乐还是办公&#xff0c;我们都离不开各种手机应用…...

编程日记 2025/8/8 8:15:08

基于大数据的酒类商品数据可视化分析系统

【大数据】基于大数据的酒类商品数据可视化分析系统 &#xff08;完整系统源码开发笔记详细部署教程&#xff09;✅ 目录 一、项目简介二、项目界面展示三、项目视频展示 一、项目简介 该系统充分利用Python与Flask的强大后端处理能力&#xff0c;结合前端Layui框架&#xff0…...

编程日记 2025/8/11 21:22:32

【数学建模】一致矩阵的应用及其在层次分析法(AHP)中的性质

一致矩阵在层次分析法(AHP)中的应用与性质 在层次分析法(AHP)中&#xff0c;一致矩阵是判断矩阵的一种理想状态&#xff0c;它反映了决策者判断的完全合理性和一致性&#xff0c;也就是为了避免决策者认为“A比B重要&#xff0c;B比C重要&#xff0c;但是C又比A重要”的矛盾。…...

编程日记 2025/8/4 14:12:24

【YOLOv8】YOLOv8改进系列（7）----替换主干网络之LSKNet

主页&#xff1a;HABUO&#x1f341;主页&#xff1a;HABUO &#x1f341;YOLOv8入门改进专栏&#x1f341; &#x1f341;如果再也不能见到你&#xff0c;祝你早安&#xff0c;午安&#xff0c;晚安&#x1f341; 【YOLOv8改进系列】&#xff1a; 【YOLOv8】YOLOv8结构解读…...

编程日记 2025/8/10 17:22:06

【MySQL】多表查询（笛卡尔积现象，联合查询、内连接、左外连接、右外连接、子查询）-通过练习快速掌握法

在DQL的基础查询中&#xff0c;我们已经学过了多表查询的一种&#xff1a;联合查询&#xff08;union&#xff09;。本文我们将系统的讲解多表查询。 笛卡尔积现象 首先&#xff0c;我们想要查询emp表和stu表两个表&#xff0c;按照我们之前的知识栈&#xff0c;我们直接使用…...

编程日记 2025/8/11 6:47:46

练习-平方拆分问题（线性筛法-筛质数）

问题描述 小蓝非常热爱数学&#xff0c;一天老师给小蓝出了一道数学题&#xff0c;想锻炼锻炼小蓝的思维能力。题目是这样的&#xff1a;给定两个数 a 和 b&#xff0c;在 a 到 b&#xff08;包括 a,b&#xff09;之间所有数的平方当中&#xff0c;试问有几个数能够表示为 xy …...

编程日记 2025/8/3 12:58:11

CVE-2018-2628(使用 docker 搭建)

介绍&#xff1a; 是一个影响 Oracle WebLogic Server 的严重漏洞&#xff0c;属于 远程代码执行&#xff08;RCE&#xff09; 漏洞。以下是对该漏洞的详细分析&#xff1a; ● 漏洞类型: 远程代码执行(RCE) ● 影响范围:Oracle WebLogic Server 10.3.6.0, 12.1.3.0, 12.2.1.2…...

编程日记 2025/8/7 5:13:19

【深度学习与大模型基础】第5章-线性相关与生成子空间

线性相关是指一组向量中&#xff0c;至少有一个向量可以表示为其他向量的线性组合。具体来说&#xff0c;对于向量组 v1,v2,…,vn&#xff0c;如果存在不全为零的标量 c1,c2,…,cn使得&#xff1a; c1v1c2v2…cnvn0 则称这些向量线性相关。否则&#xff0c;它们线性无关。 举…...

编程日记 2025/8/8 23:28:37

使用 PaddlePaddle 官方提供的 Docker 镜像

CUDA版本高PaddlePaddle不支持时&#xff0c;可以使用 PaddlePaddle 官方提供的 Docker 镜像 1. 安装 Docker Desktop1.1 下载 Docker Desktop1.2 安装 Docker Desktop1.3 启用 WSL 2 或 Hyper-V1.4 启动 Docker Desktop1.5 Docker不运行解决方法 2. 拉取 PaddlePaddle Docker …...

编程日记 2025/8/10 6:36:02

LORA: LOW-RANK ADAPTATION OF LARGE LANGUAGE MODELS 论文阅读

一、TL&#xff1b;DR 为什么要这么做&#xff1f;预训练模型越来越大&#xff0c;比如GPT-3 175B训练独立变得越来越不可行方法&#xff1a;冻结预训练模型的权重&#xff0c;在Transformer架构的每一层中注入可训练的低秩分解矩阵效果&#xff1a;训练参数量减少10000x&…...

编程日记 2025/8/11 2:50:09

企业的应用系统

一、人力资源系统 负责管理员工信息&#xff0c;处理入职&#xff0c;离职&#xff0c;调岗。 1、一般员工的信息有电子档和纸质档两份。 电子档经常是excel文件。 2、高级的公司会建立一套Web应用系统。 3、实现的功能&#xff1a; 新员工入职登记 (登记信息一般是&#xff1a…...

编程日记 2025/8/10 11:25:52

SpringBoot手动注册定时任务

一、背景 项目存在这样一个场景。程序启动过程中&#xff0c;在Spring的Bean组件注册完毕后&#xff0c;会初始化一些基础数据到数据库中&#xff0c;而项目中有部分定时任务需要依赖这些基础数据才能正常运行。如果直接使用Scheduled注解标注定时任务方法&#xff0c;会导致定…...

编程日记 2025/8/1 13:42:11

通过 Python 爬虫提高股票选股胜率

此贴为Python爬虫技术学习贴 在股票中&#xff0c;即便有了选股规则&#xff0c;从5000多只股票中筛选出符合规则的股票也是十分困难的&#xff0c;于是想通过爬虫来实现自动化的快速选股。全文用GP代替股票 实现方案 1、指定两套规则&#xff0c;第一套弱约束&#xff0c;第…...

编程日记 2025/8/7 1:55:04

InternVL：论文阅读 -- 多模态大模型(视觉语言模型)

更多内容&#xff1a;XiaoJ的知识星球 文章目录 InternVL: 扩展视觉基础模型与通用视觉语言任务对齐1.概述2.InternVL整体架构1&#xff09;大型视觉编码器&#xff1a;InternViT-6B2&#xff09;语言中间件&#xff1a;QLLaMA。3&#xff09;训练策略&#xff08;1&#xff09…...

编程日记 2025/8/9 10:45:01

代码随想录算法训练营第三十五天（20250303） |01背包问题 二维，01背包问题 一维，416. 分割等和子集 -[补卡20250316]

01背包问题 二维 链接 遍历物品没有大小顺序要求重点是模拟&#xff0c;推导出递推公式 #include <iostream> #include <vector>int main(){int m, n;std::cin>>m>>n;std::vector<int> weight(m,0),value(m,0);for(int i{0}; i<m; i){std:…...

编程日记 2025/8/9 20:46:26

RGV调度算法（三）--遗传算法

1、基于时间窗 https://wenku.baidu.com/view/470e9fd8b4360b4c2e3f5727a5e9856a57122693.html?_wkts_1741880736197&bdQuery%E7%8E%AF%E7%A9%BF%E8%B0%83%E5%BA%A6%E7%AE%97%E6%B3%95 2.2019年MathorCup高校数学建模挑战赛B题 2019-mathorcupB题-环形穿梭机调度模型&a…...

编程日记 2025/8/6 2:18:40

并发编程-

一、简述 线程&#xff1a;线程是cpu可执行的最小单位&#xff0c;而进程是操作系统可分配的最小资源单位。一个进程中可以有多个线程。 线程的五个状态&#xff1a; 新建&#xff08;new Thread()&#xff09; 就绪 &#xff08;thread.start()&#xff09; 运行&#xff08…...

编程日记 2025/8/7 22:19:49

Mac中nvm切换node版本失败，关闭终端再次打开还是之前的node

Mac中使用 nvm 管理 node 版本&#xff0c;在使用指令&#xff1a;nvm use XXX 切换版本之后。 关闭终端&#xff0c;再次打开&#xff0c;输入 node -v 还是得到之前的 node 版本。 原因&#xff1a; 在这里这个 default 中有个 node 的版本号&#xff0c;使用 nvm use 时&a…...

编程日记 2025/8/9 16:16:21

C语言（25）

一.数据在内存中的存储 1.整数在内存中的存储 整数在内存中以二进制的形式储存&#xff0c;分别为原码&#xff0c;补码&#xff0c;反码 有符号的整数&#xff0c;在上述三种形式都有符号位和数值位两个部分&#xff0c;符号位为0是正数&#xff0c;1是负数&#xff0c;最高…...

编程日记 2025/8/7 12:39:45

HTML、CSS

什么是HTML、CSS HTML结构标签及特点 CSS引入方式 CSS颜色表示形式&#xff1a; CSS引入方式、颜色表示、颜色属性 CSS选择器 超链接...

编程日记 2025/7/17 3:39:33

c#:主窗体与子控件之间的数据传递：基于事件和委托的实现

1. 概述 在WPF中&#xff0c;主窗体与子控件之间的数据传递通常通过以下两种方式实现&#xff1a; 事件&#xff08;Event&#xff09;&#xff1a;主窗体触发事件&#xff0c;子控件订阅事件并接收数据。 委托&#xff08;Delegate&#xff09;&#xff1a;通过委托将子控件…...

编程日记 2025/8/12 16:16:00

Dynamics 365 启用用户安全角色变更的审核功能

D365自身的审核功能这里就不说了&#xff0c;是一个很古老的功能&#xff0c;用过D365的人应该都知道&#xff0c;今天要说的是用户安全角色变更的审核记录。 很多人用系统的审核功能&#xff0c;更多的是用来追踪用户的登录记录&#xff0c;或者记录的修改记录。 而实际的项目…...

编程日记 2025/8/12 4:22:03

MyBatis注解

MyBatis 的注解&#xff08;Annotations&#xff09;提供了一种简洁的方式来配置 SQL 映射&#xff0c;而无需使用 XML 文件。通过在 Mapper 接口的方法上使用注解&#xff0c;可以直接在 Java 代码中定义 SQL 语句和相关映射。这种方式使得代码更加集中和易于维护&#xff0c;…...

编程日记 2025/8/12 12:12:04

1.Windows+vscode+cline+MCP配置

文章目录 1.简介与资源2.在windows中安装vscode及Cline插件1. 安装vscode2. 安装Cline插件3. 配置大语言模型3. 配置MCP步骤(windows) 1.简介与资源 MCP官方开源仓库 MCP合集网站 参考视频 2.在windows中安装vscode及Cline插件 1. 安装vscode 2. 安装Cline插件 Cline插件…...

编程日记 2025/8/11 4:26:03

94.HarmonyOS NEXT动画系统实现教程：深入理解FuncUtils

温馨提示&#xff1a;本篇博客的详细代码已发布到 git : https://gitcode.com/nutpi/HarmonyosNext 可以下载运行哦&#xff01; HarmonyOS NEXT动画系统实现教程&#xff1a;深入理解FuncUtils 文章目录 HarmonyOS NEXT动画系统实现教程&#xff1a;深入理解FuncUtils1. 动画系…...

编程日记 2025/8/6 17:56:33

Python----数据分析（Pandas一：pandas库介绍，pandas操作文件读取和保存）

一、Pandas库 1.1、概念 Pandas是一个开源的、用于数据处理和分析的Python库&#xff0c;特别适合处理表格类数 据。它建立在NumPy数组之上&#xff0c;提供了高效的数据结构和数据分析工具&#xff0c;使得数据操作变得更加简单、便捷和高效。 Pandas 的目标是成为 Python 数据…...

编程日记 2025/8/11 2:54:54

设计模式之原型模式：原理、实现与应用

引言 原型模式&#xff08;Prototype Pattern&#xff09;是一种创建型设计模式&#xff0c;它通过复制现有对象来创建新对象&#xff0c;而不是通过实例化类。原型模式特别适用于创建成本较高的对象&#xff0c;或者需要动态配置的对象。本文将深入探讨原型模式的原理、实现方…...

编程日记 2025/8/12 22:44:15

平方矩阵问题

Ⅰ 回字形二维数组 #include <iostream> #include <iomanip> using namespace std; int main(){int n;while(cin>>n,n){for(int i0; i<n;i){for(int j0; j<n; j){int upi, downn-i1, leftj, rightn-j1;cout<<min(min(up,down),min(left,right)…...

编程日记 2025/8/10 0:59:50

C语言之链表

文章目录 前言 一、链表基本概念 1、声明节点结构 2、创建节点变量 3、链表所有节点 4、遍历链表 二、add添加 三、insert插入 四、remove删除 五、查找 总结 前言 链表是一种重要的数据结构&#xff0c;用于存储和组织数据。它是由一系列节点组成的数据结构&#x…...

编程日记 2025/8/11 3:01:57

RabbitMQ延迟消息

文章目录 延迟消息死信交换机延迟消息延迟消息应用场景 延迟消息 生产者在发送消息的时候指定一个时间&#xff0c;消费者不会立即收到该消息&#xff0c;而是在指定时间之后才收到消息&#xff0c;这就是延迟消息。 比如说这么一个场景&#xff0c;用户下单后将商品库存进行…...

编程日记 2025/8/8 23:33:11

Unity中WolrdSpace下的UI展示在上层

一、问题描述 Unity 中 Canvas使用World Space布局的UI&#xff0c;想让它不被3d物体遮挡&#xff0c;始终显示在上层。 二、解决方案 使用shader解决 在 UI 的材质中禁用深度测试&#xff08;ZTest&#xff09;&#xff0c;强制 UI 始终渲染在最上层。 Shader "Custo…...

编程日记 2025/8/11 5:00:28