当前位置：首页 > news >正文

一学就会：A*算法详细介绍（Python）

news 来源：原创 2025/8/29 23:46:03

📢本篇文章是博主人工智能学习以及算法研究时，用于个人学习、研究或者欣赏使用，并基于博主对相关等领域的一些理解而记录的学习摘录和笔记，若有不当和侵权之处，指出后将会立即改正，还望谅解。文章分类在👉启发式算法专栏：

【人工智能】- 【启发式算法】（6）---《一学就会：A*算法详细介绍（Python）》

一学就会：A*算法详细介绍（Python）

A*算法介绍

A*算法的核心概念

A*算法的特点

A*算法示例：迷宫

执行步骤

第1步：初始化

第2步：扩展当前节点（起始节点）

第3步：选择下一个节点（最低 f(n)）

第4步：处理当前节点 (0,1)

第5步：继续探索

重点说明

最终结果

A*算法与其他相关算法的比较

[Python] A*算法实现

[Results] 运行结果

[Notice] 注意事项

适用场景

实现建议

A算法介绍*

A*算法是一种高效的路径搜索算法，广泛应用于人工智能、机器人技术、游戏开发等领域。它由Peter Hart、Nils Nilsson和Bertram Raphael于1968年首次提出。A算法结合了Dijkstra算法的系统性搜索和启发式搜索的优点，通过使用启发式函数来减少搜索空间，同时保证找到最短路径。

A*算法的核心概念

A*算法是一种最佳优先搜索算法，它通过以下三个关键函数来评估路径：

g(n)：从起点到当前节点的实际代价。
h(n)：从当前节点到目标节点的启发式估算代价。
f(n) = g(n) + h(n)：通过当前节点到达目标的总估算代价。

在每次迭代中，A*算法会选择具有最低f(n)值的节点进行扩展，并更新其邻居节点的代价。如果邻居节点的试探性代价低于之前记录的值，则会更新该节点的代价，并将其添加到开放集合中。这一过程会持续进行，直到找到目标节点或确定路径不存在。

A*算法的特点

最优性：当使用可接受的启发式函数时，A*算法能够找到最短路径。
效率：启发式函数的引导使得A*算法比Dijkstra算法探索更少的节点。
灵活性：启发式函数可以根据不同场景进行定制。
完整性：如果存在解决方案，A*算法将找到它。

A*算法示例：迷宫

以下是使用A*算法在一个示例迷宫中寻找路径的详细步骤说明：

假设有以下10x10的迷宫：

S 0 0 0 0 0 0 0 0 0
0 1 1 0 1 1 0 1 1 0
0 1 0 0 0 0 0 0 1 0
0 1 1 1 1 1 0 1 1 0
0 0 0 0 1 0 0 0 0 0
0 1 1 0 1 1 1 1 1 0
0 1 0 0 0 0 0 0 0 0
0 1 1 1 1 1 1 1 1 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 E

其中，S 表示起点 (0,0)，E 表示终点 (9,9)，0 表示可以通行的路径，1 表示障碍物.

执行步骤

第1步：初始化

起始节点：(0,0)，初始化其 g(n)=0，h(n) 由直线距离计算，f(n)=0+13.416=13.416。
开放列表：未被选择的节点。
封闭列表：已被选择的节点。
当前节点：起始节点。

第2步：扩展当前节点（起始节点）

邻节点：(0,1), (1,0)。
检查范围：确保邻节点在迷宫范围内。
障碍物检查：(0,1) 是 0，(1,0) 是 0。
计算邻节点g(n)：
- (0,1)：起始节点的 g(n)=0+1=1。
- (1,0)：起始节点的 g(n)=0+1=1。
计算邻节点h(n)：
- (0,1) 的 h(n)=sqrt((9-0)^2 + (9-1)^2)= sqrt(81+64)=11.401。
- (1,0) 的 h(n)=sqrt((9-1)^2 + (9-0)^2)=sqrt(64+81)=11.401。
计算邻节点f(n)：
- (0,1) 的 f(n)=1+11.401=12.401。
- (1,0) 的 f(n)=1+11.401=12.401。
在开放列表中添加邻节点：
- (0,1) 和 (1,0) 添加到开放列表。

第3步：选择下一个节点（最低 `f(n)`）

开放列表中有 (0,1) 和 (1,0)，它们的 f(n) 都是 12.401。可以选择其中任意一个：

选择 (0,1) 作为当前节点。

第4步：处理当前节点 `(0,1)`

邻节点：(0,0)（起点，已在封闭列表），(0,2)，(1,1)。
障碍物检查：
- (0,2) 是 0。
- (1,1) 是 1（障碍物）。
生成有效邻节点：(0,2)。
计算(0,2) 的 g(n)：
- 来自 (0,1)，g(n)=1+1=2。
计算(0,2) 的 h(n):
- sqrt((9-0)^2 + (9-2)^2)= sqrt(81+49)=10.630。
计算 (0,2) 的 f(n):
- 2+10.630=12.630。
将 (0,2) 添加到开放列表:
- 开放列表现在包含 (1,0), (0,2)。

第5步：继续探索

重复步骤，选择开放列表中 f(n) 最低的节点，继续扩展并更新邻节点的 g(h,f) 值，直到到达目标节点 (9,9)。

重点说明

扩展当前节点：每次从开放列表中取出 f(n) 最低的节点，生成其邻节点。
更新邻节点信息：
- 如果邻节点未被访问过，计算其 g(h,f) 并加入开放列表。
- 如果邻节点已在开放列表中，需要比较新的 g(n) 是否更小。如果更小，更新父节点和 g(n)。
终止条件：
- 当前节点是目标节点，回溯路径。
- 开放列表为空，没有路径。

最终结果

经过反复的节点扩展和评估，A* 算法最终找到从起点 (0,0) 到终点 (9,9) 的最短路径。路径将避免迷宫中的所有障碍物，确保每一步都是经过成本最低的选择。

A*算法与其他相关算法的比较

算法	与A*的关系	关键差异	优缺点
Dijkstra算法	A*是Dijkstra算法的扩展	A*使用f(n)=g(n)+h(n)，Dijkstra仅使用g(n)	A*在有启发式函数时性能更好，Dijkstra无需启发式函数
Bellman-Ford算法	基于边的松弛	Bellman-Ford支持负边权重，A*通常更快	Bellman-Ford适用于有负权重的图，A*需要启发式函数
Floyd-Warshall算法	解决所有点对最短路径问题	Floyd-Warshall使用动态规划，A*是增量搜索	Floyd-Warshall适合密集图，A*适合实时路径搜索

[Python] A*算法实现

项目代码我已经放入下面链接里面：🔥

A*算法实现

若是下面代码复现困难或者有问题，也欢迎评论区留言。

"""《A*算法实现》时间：2025.02.27环境：迷宫作者：不去幼儿园
"""
import heapq
import matplotlib.pyplot as plt
import numpy as npclass Node:"""节点类表示搜索树中的每一个点。"""def __init__(self, parent=None, position=None):self.parent = parent        # 该节点的父节点self.position = position    # 节点在迷宫中的坐标位置self.g = 0                  # G值：从起点到当前节点的成本self.h = 0                  # H值：当前节点到目标点的估计成本self.f = 0                  # F值：G值与H值的和，即节点的总评估成本# 比较两个节点位置是否相同def __eq__(self, other):return self.position == other.position# 定义小于操作，以便在优先队列中进行比较def __lt__(self, other):return self.f < other.fdef astar(maze, start, end):"""A*算法实现，用于在迷宫中找到从起点到终点的最短路径。"""start_node = Node(None, start)  # 创建起始节点end_node = Node(None, end)      # 创建终点节点open_list = []                  # 开放列表用于存储待访问的节点closed_list = []                # 封闭列表用于存储已访问的节点heapq.heappush(open_list, (start_node.f, start_node))  # 将起始节点添加到开放列表while open_list:current_node = heapq.heappop(open_list)[1]  # 弹出并返回开放列表中 f 值最小的节点closed_list.append(current_node)            # 将当前节点添加到封闭列表if current_node == end_node:  # 如果当前节点是目标节点，则回溯路径path = []while current_node:path.append(current_node.position)current_node = current_node.parentreturn path[::-1]  # 返回反向路径，即从起点到终点的路径(x, y) = current_node.positionneighbors = [(x-1, y), (x+1, y), (x, y-1), (x, y+1)]  # 获取当前节点周围的相邻节点for next in neighbors:if 0 <= next[0] < maze.shape[0] and 0 <= next[1] < maze.shape[1]:  # 确保相邻节点在迷宫范围内if maze[next[0], next[1]] == 1:  # 如果相邻节点是障碍物，跳过continueneighbor = Node(current_node, next)  # 创建相邻节点if neighbor in closed_list:  # 如果相邻节点已在封闭列表中，跳过不处理continueneighbor.g = current_node.g + 1  # 计算相邻节点的 G 值neighbor.h = ((end_node.position[0] - next[0]) ** 2) + ((end_node.position[1] - next[1]) ** 2)  # 计算 H 值neighbor.f = neighbor.g + neighbor.h  # 计算 F 值if add_to_open(open_list, neighbor):  # 如果相邻节点的新 F 值较小，则将其添加到开放列表heapq.heappush(open_list, (neighbor.f, neighbor))return None  # 如果没有找到路径，返回 Nonedef add_to_open(open_list, neighbor):"""检查并添加节点到开放列表。"""for node in open_list:if neighbor == node[1] and neighbor.g > node[1].g:return Falsereturn True  # 如果不存在，则返回 True 以便添加该节点到开放列表def visualize_path(maze, path, start, end):"""将找到的路径可视化在迷宫上。"""maze_copy = np.array(maze)for step in path:maze_copy[step] = 0.5  # 标记路径上的点plt.figure(figsize=(10, 10))plt.imshow(maze_copy, cmap='hot', interpolation='nearest')path_x = [p[1] for p in path]  # 列坐标path_y = [p[0] for p in path]  # 行坐标plt.plot(path_x, path_y, color='orange', linewidth=2)start_x, start_y = start[1], start[0]end_x, end_y = end[1], end[0]plt.scatter([start_x], [start_y], color='green', s=100, label='Start', zorder=5)  # 起点为绿色圆点plt.scatter([end_x], [end_y], color='red', s=100, label='End', zorder=5)  # 终点为红色圆点plt.legend()plt.show()

# 设定迷宫的尺寸
maze_size = 100
maze = np.zeros((maze_size, maze_size))
obstacle_blocks = [(10, 10, 20, 20),  # (y起始, x起始, 高度, 宽度)(30, 40, 20, 30),(60, 20, 15, 10),(80, 50, 10, 45),
]
for y_start, x_start, height, width in obstacle_blocks:maze[y_start:y_start+height, x_start:x_start+width] = 1
start = (0, 0)
end = (92, 93)
maze[start] = 0
maze[end] = 0
path = astar(maze, start, end)
if path:print("路径已找到：", path)visualize_path(maze, path, start, end)
else:print("没有找到路径。")

[Results] 运行结果

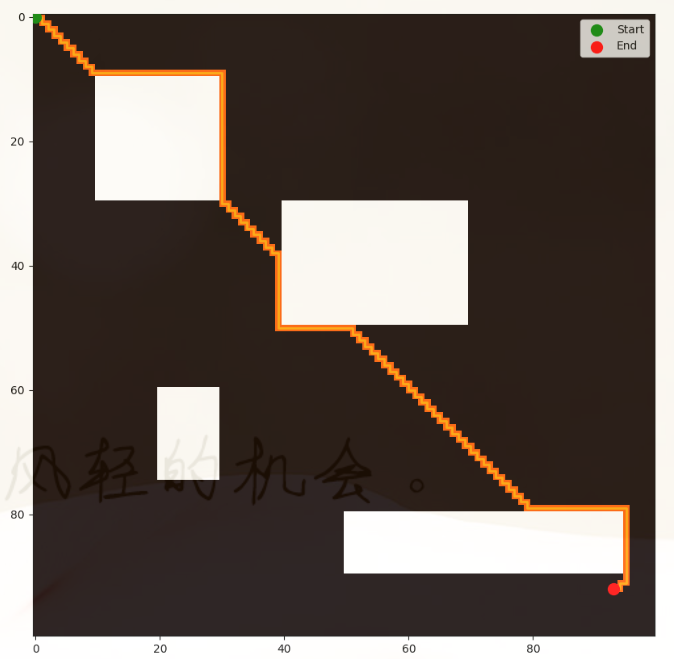
[Notice] 注意事项

# 环境配置
Python                  3.11.5
torch                   2.1.0
torchvision             0.16.0
gym                     0.26.2

由于博文主要为了介绍相关算法的原理和应用的方法，缺乏对于实际效果的关注，算法可能在上述环境中的效果不佳或者无法运行，一是算法不适配上述环境，二是算法未调参和优化，三是没有呈现完整的代码，四是等等。上述代码用于了解和学习算法足够了，但若是想直接将上面代码应用于实际项目中，还需要进行修改。

适用场景

A*算法最适合以下场景：

单源单目标路径搜索。
可以提供领域特定的启发式函数。
需要最优解。
有足够的内存来维护开放/关闭集合。

主要应用场景

迷宫寻路：在游戏开发中，A*算法可以用来为游戏角色找到从起点到终点的最短路径，例如在迷宫类游戏中，角色需要绕过障碍物尽快到达目标。
机器人路径规划：在机器人领域，A*算法可用于规划机器人在复杂环境中的移动路径，帮助其避开障碍物并找到到达目标位置的最佳路线。
地图导航：在 GPS 导航系统或地图应用中，A*算法可以计算两点之间的最短路径，考虑道路长度、交通状况等多种因素，为用户提供最优的行驶路线建议。

实现建议

使用优先队列（如二叉堆或斐波那契堆）快速选择节点。
根据图的大小选择合适的数据结构。
设计并验证有效的启发式函数。

算法优点

寻找最短路径：无论是二维平面还是三维空间，A*算法都能够有效地在复杂的环境图中找到从起点到终点的最短路径，尤其是在具有障碍物和多重路径选择的情况下。
优化效率：相比传统的广度优先搜索和深度优先搜索，A*算法通过结合启发式估计和实际路径成本，能够更高效地探索可能的路径，减少不必要的计算，大大提升了路径寻找的效率。
适应复杂环境：A*算法能够灵活地处理各种环境变化，如新增障碍物、改变目标位置等，只需重新计算路径即可，无需对整个地图进行重新规划。

实现效果

准确性：A*算法能够精确地找到最优路径，确保路径的总成本（如距离、时间等）最小，对于大多数场景来说，其结果都是全局最优的。
实时性：在处理复杂地图时，A*算法能够在较短时间内完成路径规划，满足实时性要求，特别是在一些动态环境（如即时战略游戏或动态交通导航）中。
可视化：通过可视化工具，可以清晰地看到 A*算法的搜索过程，路径是如何被逐步探索和确定的，这对于调试和理解算法的工作原理非常有帮助。

更多启发式算法文章，请前往：【启发式算法】专栏

博客都是给自己看的笔记，如有误导深表抱歉。文章若有不当和不正确之处，还望理解与指出。由于部分文字、图片等来源于互联网，无法核实真实出处，如涉及相关争议，请联系博主删除。如有错误、疑问和侵权，欢迎评论留言联系作者，或者添加VX：Rainbook_2，联系作者。✨

一学就会：A*算法详细介绍（Python）

📢本篇文章是博主人工智能学习以及算法研究时，用于个人学习、研究或者欣赏使用，并基于博主对相关等领域的一些理解而记录的学习摘录和笔记，若有不当和侵权之处，指出后将会立即改正，还望谅解。文章分类在&am…...

编程日记 2025/8/29 23:46:03

【Elasticsearch】Elasticsearch 中使用 HDFS 存储快照

在 Elasticsearch 中使用 HDFS 存储快照的步骤如下： 1.安装 HDFS 插件要使用 HDFS 存储 Elasticsearch 的索引快照，需要在 Elasticsearch 集群的所有节点上安装 HDFS 插件。 • 在线安装：适用于网络环境良好的场景，执行以下命…...

编程日记 2025/8/29 23:44:06

【每日十题系列】前端面试高频题目

以下是作为前端面试官常用的10道手撕代码题目，涵盖JavaScript核心、CSS、算法及框架原理，结合高频考点与实际开发场景设计： 1. 手写防抖（debounce）与节流（throttle） 要求：实现防抖函…...

编程日记 2025/8/24 14:33:22

Kafka 消息 0 丢失的最佳实践

文章目录 Kafka 消息 0 丢失的最佳实践生产者端的最佳实践使用带有回调的 producer.send(msg, callback) 方法设置 acks all设置 retries 为一个较大的值启用幂等性与事务（Kafka 0.11）正确关闭生产者与 flush() 方法 Broker 端的最佳实践设置 unclean.l…...

编程日记 2025/8/29 23:42:13

学网络安全报班可靠吗？

在当今社会，网络安全已经成为我们工作和生活中不可忽视的重要部分，而且市场上各大企业对网络安全人才的需求量非常之大，因此网络安全培训班应运而生，那么学网络安全报培训班靠谱吗?这是很多小伙伴都关心的问题，我们来…...

编程日记 2025/8/29 23:42:14

LeetCode 1745.分割回文串 IV：动态规划（用III或II能直接秒）

【LetMeFly】1745.分割回文串 IV：动态规划（用III或II能直接秒） 力扣题目链接：https://leetcode.cn/problems/palindrome-partitioning-iv/ 给你一个字符串 s ，如果可以将它分割成三个非空回文子字符串，…...

编程日记 2025/8/29 23:42:25

4 Redis4 List命令类型讲解

Redis 列表（List）命令详解 1. Redis 列表（List）简介 Redis 列表（List）是一个简单的字符串列表，按照插入顺序排序。它可以用作栈（Stack） 和队列（Queue&…...

编程日记 2025/8/29 23:40:13

鬼泣：项目前置设置杂项

能帮到你的话，就给个赞吧 😘 文章目录插件niagara ui render：在 UI 中渲染 Niagara 特效skeletal editor：编辑骨骼，调整骨骼动画motion warping：根据目标自动调整角色动画。animation warping：…...

编程日记 2025/8/28 21:22:49

MyBatis-Plus 条件构造器的使用（左匹配查询）

在上一篇文章中，我们已经介绍了 MyBatis-Plus 条件构造器，包括 QueryWrapper 和 UpdateWrapper 的基本使用方法、常见查询条件（如等于、不等于、大于、小于）以及如何使用 Lambda 表达式来构建动态查询和更新条件。在本文中&…...

编程日记 2025/8/25 22:34:43

#define GBB_DEPRECATED_MSG(msg) __declspec(deprecated(msg))

这个宏 #define GBB_DEPRECATED_MSG(msg) __declspec(deprecated(msg)) 是用来在 C++ 中标记某些函数、变量或者代码元素为已弃用（deprecated）的，并附带一个自定义的弃用消息。具体解释： __declspec(deprecated(msg))： __declspec 是 Microsoft Visual C++ (MSVC) 的扩展…...

编程日记 2025/8/21 16:07:42

Vue输入框获取焦点

1. 元素未渲染完成如果你在组件挂载或数据更新后立即调用 focus()，可能元素还未渲染到 DOM 中，导致 focus() 失效。解决方法：确保在元素渲染完成后再调用 focus()。可以使用 nextTick 确保 DOM 更新完成。 2. ref 未正确绑定确保 ref 正确…...

编程日记 2025/8/27 11:07:22

辛格迪客户案例 | 深圳善康医药科技GMP培训管理（TMS）项目

01 善康医药：创新药领域的探索者深圳善康医药科技股份有限公司自2017年创立以来，便扎根于创新药研发领域，专注于成瘾治疗药物的研究、生产与销售。公司坐落于深圳，凭借自身独特的技术优势与研发实力，在行业内逐渐崭露…...

编程日记 2025/8/28 1:48:17

迷你世界脚本出生点接口：Spawnport

出生点接口：Spawnport 彼得兔更新时间: 2023-04-26 10:19:56 具体函数名及描述如下: 序号函数名函数描述 1 getSpawnPoint(...) 获取默认出生点 2 setSpawnPoint(...) 设置出生点位置 3 getChunkValidSpawnPos(...) 获取区块有效刷新点…...

编程日记 2025/8/29 10:19:23

Android车机DIY开发之软件篇(二十)立创泰山派android编译

准备工作 sudo apt-get update sudo apt-get install git -y sudo apt install repo -ysudo apt-get install python2.7sudo apt-get install python3sudo update-alternatives --install /usr/bin/python python /usr/bin/python2.7 1 sudo update-alternatives --install /u…...

编程日记 2025/8/29 7:06:28

MDM 如何彻底改变医疗设备的远程管理

在现代医疗行业迅速发展的格局中，医院和诊所越来越依赖诸如医疗平板和移动工作站等移动设备。这些设备在提高工作效率和提供卓越的患者护理方面发挥着关键作用。然而，随着它们的广泛使用，也带来了一系列挑战，例如在不同地点确保数…...

编程日记 2025/8/29 16:02:33

Libgdx游戏开发系列教程(6)——游戏暂停

目录最初方案1 优化方案2 - 事件拦截器监听按键优化方案3 - 暂停状态重绘优化方案4 优化方案5 补充 - 监听android手机的返回键暂停也是一个游戏的必要功能了,本文研究了Libgdx实现游戏暂停例子以桌面端游戏实现讲解为主,至于移动端,可能之后会进行补充... 本文最…...

编程日记 2025/8/29 17:41:00

车载测试：智能座舱测试中多屏联动与语音交互的挑战

智能座舱作为汽车智能化发展的核心，集成了多屏联动和语音交互功能，为驾驶员和乘客提供更便捷的体验。然而，这些功能的测试面临诸多挑战，包括多屏同步性、噪声干扰和复杂场景的处理。本文将详细分析这些挑战，探讨测试方…...

编程日记 2025/8/29 16:16:03

【踩坑随笔】`npm list axios echarts`查看npm依赖包报错

npm list axios echarts查看npm依赖包出现以下报错，原因就是包的版本匹配问题，按照提示降axios版本或者自己升找合适的got版本，我这里是选择了降版本。本文记录仅做解决思路参考不一定适配大家的实际情况。 weed-detection-system1.0.0 E:\P…...

编程日记 2025/8/28 16:45:10

用于管理 Elasticsearch Serverless 项目的 AI Agent

作者：来自 Elastic Fram Souza 由自然语言驱动的 AI 代理，可轻松管理 Elasticsearch Serverless 项目 - 支持项目创建、删除和状态检查。这个小型命令行工具让你可以用简单的英语管理你的无服务器 Elasticsearch 项目。它通过AI（这里是 Ope…...

编程日记 2025/8/28 8:34:23

【文生图】windows 部署stable-diffusion-webui

windows 部署stable-diffusion-webui AUTOMATIC1111 stable-diffusion-webui Detailed feature showcase with images: 带图片的详细功能展示： Original txt2img and img2img modes 原始的 txt2img 和 img2img 模式 One click install and run script (but you still must i…...

编程日记 2025/8/29 17:19:50

STaR（Self-Taught Reasoner）方法：让语言模型自学推理能力（代码实现）

STaR（Self-Taught Reasoner）方法：让语言模型自学推理能力在大型语言模型（LLM）的推理能力优化中，STaR（Self-Taught Reasoner） 是一种引人注目的技术，属于“修改提议分布…...

编程日记 2025/8/26 17:38:26

十大经典排序算法简介

一概述本文对十大经典排序算法做简要的总结（按常用分类方式排列），包含核心思想、时间/空间复杂度及特点。二、比较类排序 1. 冒泡排序 (BUBBLE SORT) 思想：重复交换相邻逆序元素，像气泡上浮复杂度：时间：O(n^2)（最好情况O(n)）空间：O(1) 特点：简单但效率低，稳…...

编程日记 2025/8/28 21:10:16

5.训练策略：优化深度学习训练过程的实践指南——大模型开发深度学习理论基础

在实际开发中，训练策略对神经网络的表现起着至关重要的作用。通过合理的训练策略，我们可以有效避免过拟合和欠拟合，加速模型收敛，并提升最终性能。本文将从实际开发角度详细介绍几种关键的训练策略，包括 Early Stoppin…...

编程日记 2025/8/28 10:58:58

道可云人工智能每日资讯｜《奇遇三星堆》VR沉浸探索展（淮安站）开展

道可云元宇宙每日简报（2025年3月5日）讯，今日元宇宙新鲜事有： 《奇遇三星堆》VR沉浸探索展（淮安站）开展近日，《奇遇三星堆》VR沉浸探索展（淮安站）开展。该展将三星堆文…...

编程日记 2025/8/27 14:20:53

Camera相关配置

一、 Purpose目的通常， 感知模块使用雷达点云和相机图像来对物体进行检测和分类，感知数据分别来自雷达和相机，就传感器数据融合准确性，我们需要雷达和相机同一时间捕捉到同一物体(时间间隔尽可能短)，否则一个真实的物…...

编程日记 2025/8/28 0:37:57

PHP Error处理指南

PHP Error处理指南引言在PHP开发过程中，错误处理是一个至关重要的环节。正确的错误处理不仅能够提高代码的健壮性，还能提升用户体验。本文将详细介绍PHP中常见的错误类型、错误处理机制以及最佳实践，帮助开发者更好地应对和处理PHP错误。 PHP错误类型在PHP中，错误主…...

编程日记 2025/8/29 19:44:56

【Pandas】pandas Series argmax

Pandas2.2 Series Computations descriptive stats 方法描述Series.argsort([axis, kind, order, stable])用于返回 Series 中元素排序后的索引位置的方法Series.argmin([axis, skipna])用于返回 Series 中最小值索引位置的方法Series.argmax([axis, skipna])用于返回 Series…...

编程日记 2025/8/29 22:31:52

Gitlab配置personal access token

1.点击左上角个人账号 -> Preferences 2. 点击左边栏 Access Tokens 3. 点击Add new token ，输入token名称，勾选权限（注意截至日期 “Expiration date” 可不填） 4. 创建成功后，显示token信息，复制到本地…...

编程日记 2025/8/28 12:31:35

【MySQL、Oracle、SQLserver、postgresql】查询多条数据合并成一行

四大数据库多行合并为单行：函数详解与对比一、MySQL**GROUP_CONCAT()** 函数说明：语法结构：参数解释：示例：注意事项： 二、Oracle**LISTAGG()** 函数说明：语法结构：参数解释&#xf…...

编程日记 2025/8/29 1:27:35

人机交互进化论：解码智能手机81种交互方式背后的用户体验革命

人机交互进化论：解码智能手机81种交互方式背后的用户体验革命 2023年艾瑞咨询报告显示：中国智能手机用户日均触屏交互超2500次，解锁屏幕达76次/天。在这看似简单的点击与滑动背后，隐藏着一场持续演进的人机交互革命。本文将深度解…...

编程日记 2025/8/27 13:41:54

OCPP扩展机制与自定义功能开发：协议灵活性设计与实践 - 慧知开源充电桩平台

OCPP扩展机制与自定义功能开发：协议灵活性设计与实践引言 OCPP作为开放协议，其核心价值在于平衡标准化与可扩展性。面对不同充电桩厂商的硬件差异、区域能源政策及定制化业务需求，OCPP通过**扩展点（Extension Points&#xff09…...

编程日记 2025/8/24 0:29:12

网络编程之TCP协议

传输层协议：UDP和TCP的区别 UDP：用户数据报协议 1.面向数据报 2.无连接 3.不安全，不可靠(尽最大努力交付) TCP:传输控制协议 1.面向数据流(流式套接字) 2.建立连接 3.安全可靠的传输协议 TCP的传输过程三次握手：TCP建立…...

编程日记 2025/8/28 12:45:49

策略模式的C++实现示例

核心思想策略模式是一种行为型设计模式，它定义了一系列算法，并将每个算法封装在独立的类中，使得它们可以互相替换。策略模式让算法的变化独立于使用它的客户端，从而使得客户端可以根据需要动态切换算法，而不需要修改…...

编程日记 2025/8/29 0:07:29

keil软件下载安装使用(STM32篇)

一、前言 Keil软件是一款专为嵌入式系统开发设计的集成开发环境（IDE），由德国Keil公司创立，后被ARM公司收购并持续更新维护。它集成了代码编辑、编译、调试和项目管理等功能，广泛应用于各类单片机的程序开发&#xff0…...

编程日记 2025/8/29 8:08:49

【简单的C++围棋游戏开发示例】

C围棋游戏开发简单示例（控制台版） ‌核心代码实现‌ #include <iostream> #include <vector> #include <queue> using namespace std;const int SIZE 9; // 简化棋盘为9x9‌:ml-citation{ref"1" data"citationList&…...

编程日记 2025/8/27 3:38:26

【Python 数据结构 4.单向链表】

目录一、单向链表的基本概念 1.单向链表的概念 2.单向链表的元素插入元素插入的步骤 3.单向链表的元素删除元素删除的步骤 4.单向链表的元素查找元素查找的步骤 5.单向链表的元素索引元素索引的步骤 6.单向链表的元素修改元素修改的步骤二、Python中的单向链表编辑三…...

编程日记 2025/8/28 12:14:40

组合逻辑和时序逻辑

组合逻辑定义组合逻辑电路是一种输出只取决于当前输入值的电路，即电路的输出状态仅由当前时刻的输入信号组合决定，与电路过去的状态无关。特点无记忆功能：组合逻辑电路不具备存储信息的能力，它不会记住之前的输入情况。每次…...

编程日记 2025/8/21 2:54:53

如何有效判断与排查Java GC问题

目录一、GC的重要性与对性能的影响 （一）GC对性能的影响简要分析 1.GC暂停与应用停顿 2.GC吞吐量与资源利用率 3.GC对内存管理的作用：资源回收 4.GC策略与优化的选择 （二）GC的双刃剑二、GC性能评价标准 &…...

编程日记 2025/8/28 1:19:26

Ubuntu20.04 在离线机器上安装 NVIDIA Container Toolkit

步骤 1.下载4个安装包 Index of /nvidia-docker/libnvidia-container/stable/ nvidia-container-toolkit-base_1.13.5-1_amd64.deb libnvidia-container1_1.13.5-1_amd64.deb libnvidia-container-tools_1.13.5-1_amd64.deb nvidia-container-toolkit_1.13.5-1_amd64.deb 步…...

编程日记 2025/8/26 20:52:02

【流行病学】Melodi-Presto因果关联工具

title: “[流行病学] Melodi Presto因果关联工具” date: 2022-12-08 lastmod: 2022-12-08 draft: false tags: [“流行病学”,“因果关联工具”] toc: true autoCollapseToc: true 阅读介绍 Melodi-Presto: A fast and agile tool to explore semantic triples derived from …...

编程日记 2025/8/27 6:15:50

Android14 OTA差分包升级报Package is for source build

制作好差分包，使用adb线刷模式验证ota升级，出现E:Package is for source build错误使用adb方式验证进入recovery模式 adb reboot recovery稍等一会界面会提示 Now send the package you want to apply to the device with "adb sidelaod <…...

编程日记 2025/8/29 4:15:56

PTA L2一些题目

L2-014 列车调度 - 团体程序设计天梯赛-练习集样例是怎么来的呢？通过题目我们知道每一条轨道的车牌号必须是依次递减的。那么，我们如果让每条轨道尽可能长就能保证轨道数最少------也就是说，我们要尽可能的找最长降序序列。但是1e5数据量…...

编程日记 2025/8/29 12:15:16

Harbor端口更改||Harbor端口映射

Harbor端口更改|Harbor端口映射目标：将端口更改为8930 前言 [rootk8s-node1 harbor]# ls common common.sh docker-compose.yml harbor.v2.5.0.tar.gz harbor.yml harbor.yml.tmpl install.sh LICENSE prepare如上是Harbor的文件目录更改harbor.yml文件…...

编程日记 2025/8/28 1:34:42

基于STM32的智能家居蓝牙系统（论文+源码）

1总体方案设计本次基于STM32的智能家居蓝牙系统，其系统总体架构如图2.1所示，采用STM32f103单片机作为控制器，通过DHT11传感器实现温湿度检测，MQ-2烟雾传感器实现烟雾检测，光敏电阻实现光照检测，同时将数据…...

编程日记 2025/8/26 18:14:56

视觉Transformer（DETR）

文章目录 DETR总体流程DETR 中 transformer 结构encoderdecoderObeject Query HEADFFNLOSS正负样本分配简单的demo不足之处 DETR 是首次将 Transformer结构首次应用到视觉目标检测中，实现端到端的目标检测。传统目标检测路线（yolo代表&#xff09…...

编程日记 2025/8/26 17:05:30