P4064 [JXOI2017] 加法 蓝
题意
可怜有一个长度为 \(n\) 的正整数序列 \(A\)，但是她觉得 \(A\) 中的数字太小了，这让她很不开心。
于是她选择了 \(m\) 个区间 \([l_i,r_i]\) 和两个正整数 \(a,k\)。她打算从这 \(m\) 个区间里选出恰好 \(k\) 个区间，并对每个区间执行一次区间加 \(a\) 的操作。（每个区间最多只能选择一次）。
对区间 \([l,r]\) 进行一次加 \(a\) 操作可以定义为对于所有 \(i\) ∈ \([l,r]\)，将 \(A_i\) 变成 \(A_i+a\)。现在可怜想要知道怎么选择区间才能让操作后的序列的最小值尽可能的大，即最大化 \(\min\{A_i\}\)。
题解
二分答案，然后对区间扫描线，每次选择 \(r\) 最大的区间进行操作即可。
提交记录
P3744 李彬的几何 蓝
题意
已知多边形 \(\text{P}\)，求最小的实数 D，使得存在一种点的移动方案，满足每个顶点最多移动 D 个单位距离，且移动后 \(\text{P}\) 不再是凸多边形。
题解
发现最优情况肯定是把相邻三点变成一条直线，枚举相邻三点，计算点到直线的距离即可。
提交记录
P3895 [湖南集训] Hungry Rabbit 紫
题意
兔子王国中有 \(n\) 只兔子，在接下来的 \(m\) 天中，每天恰好有 \(k\) 只兔子去觅食。
给定一张 01 表，\(a_{i,j}\) 表示兔子 \(i\) 是否能在第 \(j\) 天觅食。\(\text{1}\) 表示可以，\(\text{0}\) 表示不可以。
令 \(p_i\) 表示第 \(i\) 天出来觅食，但是第 \(i−1\) 天却没有出来觅食的兔子个数。规定 \(p_1=0\)。
要求 \(\max p_i\leq l\)，构造一个合法的方案。
\(1\leq n,m\leq 800,\)，\(1\leq k\leq n\)，\(1\leq l\leq k\)。
题解
显然存在一个最优解满足过期早的兔子比过期晚的兔子先换下，因此每次按过期时间贪心更换 \(l\) 个即可。
提交记录
P3244 [HNOI2015] 落忆枫音 紫
题意
给定一个只有 \(1\) 号点入度为 \(0\) 的 DAG，在这个 DAG 基础上加一条有向边 \((u,v)\)，求新图的外向生成树个数。
\(n,m\leq 2\times 10^5\)。
题解
首先，对于一个 DAG，其生成树个数为 \(\prod in_i\)，相当于每个点在选一个父亲，除了 \(1\) 每个点都连向拓扑序更小的点，可以证明这一定是一棵树。
我们对新图也按这种方法计算，容易发现算多的部分是“生成树”包含了一个环，且这个环上必定有一条边 \((u,v)\)。
假设存在一个环 \((v_1,v_2,\dots,v_k)\)，那么算多的部分就是 \(\frac{\prod_{i=1}^n in_i}{\prod_{i=1}^k v_i}\)。
由于所有环在 \((u,v)\)，考查 \(u\) 节点的“父亲”可以证明：我们的假生成树最多包含一个环。
所以环与环对于多算的贡献是相互独立的，也就是说我们可以对于每个环 \((v_1,v_2,\dots,v_k)\)，都将答案减去 \(\frac{\prod_{i=1}^n in_i}{\prod_{i=1}^k v_i}\)，最终得到的答案即为正确答案。
统计新图的入度，然后在原 DAG 上 DP 出所有 \((u\to v)\) 的路径 \((v_1,v_2,\dots,v_k)\) 的 \(\frac{1}{\prod_{i=1}^k v_i}\) 之和即可。
提交记录
[ARC103D] Distance Sums 紫
题意
给定一个长度为 \(N\) 的数列 \(D_1, D_2, \ldots, D_N\)。所有 \(D_i\) 的值都互不相同。构造一个具有 \(N\) 个顶点的树，满足以下条件：
- 每个顶点都标有 \(1, 2, \ldots, N\) 的编号
- 每条边都标有 \(1, 2, \ldots, N-1\) 的编号，第 \(i\) 条边连接顶点 \(u_i\) 和 \(v_i\)
- 对于每个顶点 \(i\)，从 \(i\) 到其他所有顶点的距离之和为 \(D_i\)。这里，每条边的长度都视为 \(1\)。
题解
\(D\) 互不相同启示我们从特殊点开始构造，\(D\) 最小的是重心，但是发现从重心构造做不下去，所以考虑从叶子构造。
发现 \(D\) 最大的肯定是叶子，且与 \(D\) 比它小 \(n-2\) 的点连边。
进一步，对于一个大小为 \(sz\) 的子树，记其根为 \(rt\)，则有 \(D_{fa_{rt}}=D_{rt}-n+2\times sz\)，由于 \(D\) 互不相同，所以每棵子树的 \(fa\) 确定，按 \(D\) 从大到小构造即可。
由于我们只管了 \(D\) 之间的差值而没有管具体数值，所以构造完要检验。
提交记录
CF842E Nikita and game *2800
题意
一棵树初始只有一个编号为 \(1\) 的根结点。\(n\) 次操作，每次新增一个点作为 \(p_i\) 的子结点，询问更新后有多少点可以作为树直径的端点。
题解
利用“一个点的最远点必定是直径端点”的性质可证一个点作为直径端点的时间是一个区间。
同时可以使用上述性质维护每一时刻的直径端点，二分每个点作为直径端点的时间区间即可。
提交记录
CF2108E Spruce Dispute *2600
题意
给定一棵树，你要选择相邻两点并缩成一个点，然后将点两两匹配，两点匹配的权值是两点的树上距离。
请最大化匹配权值。
\(n\leq 2\times 10^5\)，\(n\) 是奇数。
题解
树上最大匹配的套路是找出重心然后让所有匹配都跨重心，这样是最优的，每个点的贡献是其到重心的距离。
然后由于一次缩点后重心仍然是重心，所以先按不缩点计算每个点的贡献。然后计算缩每对点的变化量即可。
提交记录
CF1783G Weighed Tree Radius *2800
题意
给你一个 \(n\) 个点的树。第 \(i\) 个点的初始权值为 \(a_i\)。定义结点 \(v\) 到结点 \(u\) 的距离 \(d_v(u)\) 等于 \(v\) 和 \(u\) 之间的边的数量。
定义结点 \(v\) 到结点 \(u\) 的权值距离 \(w_v(u)=d_v(u)+a_u\)。定义结点 \(v\) 的偏心距 \(e(v)\) 是从 \(v\) 到其他结点的最大权值距离（包括\(v\)本身），即 \(e(v)=\max\limits_{1\leq u \leq n} w_v(u)\)。定义树的半径 \(r\) 是所有偏心距的最小值，即 \(r=\min\limits_{1\leq v\leq n} e(v)\)
你需要对 \(m\) 次询问进行回答，对于第 \(j\) 次询问，给出两个数 \(v_j\) 和 \(x_j\)，表示将 \(a_{v_j}\) 的值修改为 \(x_j\)。在每次询问后，输出当前该树的半径 \(r\)。
\(n\leq 3\times 10^5\)。
题解
令两个点 \(u,v\) 的距离为 \(\operatorname{dis}(u,v)+a_u+a_v\)，则答案为 \(\max a\) 和 \(\frac{直径长度}{2}\) 的最大值。
证明如下：可以把这个定义理解为每个点下挂了 \(a\) 个点的链，如果直径中点为原树上的点，那么结论显然成立，否则说明一个点的 \(a\) 已经超过直径的一半，那么答案一定大于这个点的 \(a\)，且这个点的偏心距为 \(a\)。
由于题目带修，需要使用线段树维护直径。
提交记录
[AGC018D] Tree and Hamilton Path 紫
题意
给定一棵树 \(T\)，边有边权，完全图 \(G\) 上的两点距离为两点在树 \(T\) 上的距离。
求 \(G\) 的最长哈密顿路径。
\(n\leq 10^5\)。
题解
与树上匹配那题做法相同，找出重心然后从重心出发，保证每次行走都跨越重心，如果有两个重心就在第二个重心停止，否则就在重心邻居中邻边权值最小的邻居处停止。
提交记录
QOJ 8650. Island Hopping
题意
这是一道交互题。
交互库有一棵 \(n\) 个节点的树，你可以对交互库进行形如 \(qry(x,k)\) 的询问，交互库会告诉你距离 \(x\) 第 \(k\) 小的节点编号（如有多个距离最小的点，则按第二关键字排序），你需要在 \(2n\) 次询问内确定树的形态。
题解
考虑如果我们知道每个点的度数，那么就可以通过重复【度数】次 \(qry\) 查询这个点的所有邻居，就能确定树的形态。
我们不知道每个点的度数，也就不知道我们何时才能停止调用 \(qry\)，而度数是不好求的。
让我们换一种思路，我们对一个点重复调用 \(qry\) 直到我们得到的结果是这个点的父亲。
判断相邻点的父子关系是简单的，我们可以先调用 \(qry(1,2\sim n)\) 来得出 bfs 序，然后判断一个点的bfs序是否小于另一个点。
然后我们对于每个点不断调用 \(qry\) 直到我们得到一个 bfs 序比当前小的点作为这个点的父亲。至此我们会了 \(3n\) 次调用的做法（\(n-1\) 定 bfs 序，\(2n-2\) 定每个点的父亲）
然后我们发现我们不断调用 \(qry\) 时会浪费很多信息，因此考虑把这些信息利用起来，我们按照 bfs 序从小到大进行操作，不断调用 \(qry\) 直到我们得到一个 bfs 序比当前小的点作为这个点的父亲，对于知道父亲之前的每个点 \(p\)，更新 \(fa_p=now\)，然后处理一个点时，如果这个点父亲以确定就跳过。
这样我们就做到了 \(n-1\) 次操作定每个点的父亲，总共 \(2n-2\) 次操作。
提交记录
NOIP 模拟赛 T4 tree
题意
给定一棵有 \(N\) 个节点的点带权无根树。现在，你需要选择一些互不相交（包括端点）的路径。如果你选择了 \(K\) 条路径，且覆盖的点权和为 \(S\)，你的得分即为 \(\frac{S}{K+1}\)。
另外，在选取路径之前，你必须执行一次如下操作（操作分为三个步骤）：
- 选定一个参数 \(C\)，满足 \(C \in [0, T]\)
- 将所有的点权 \(+C\)
- 将所有的点权对 \(LIMIT\) 取模
其中，\(T\)、\(LIMIT\) 的值已经被给出。你的任务就是求出可能的最高得分。
要求 \(O(n^2)\)。
题解
发现只有 \(O(n)\) 个有用的 \(C\)，枚举这些 \(C\)。
然后我们要解决树上选若干不交路径，最大化 \(\frac{S}{K+1}\)。这是一个经典的分数规划问题，二分答案后将所有路径减去 \(mid\)。
然后树形 DP 检验，时间复杂度 \(O(n^2\log V)\)。
对有用的 \(C\) 以随机顺序枚举，并做最优性剪枝，那么我们进行二分的次数就是随机序列前缀 \(\max\) 的期望个数，即 \(O(\log n)\)，因此总期望复杂度 \(O(n^2+n\log^2 n)\)。
提交记录
NOIP 模拟赛 T3 circle
题意
有一个环，环上有 \(2^M\) 个位置，用 \(0 \sim 2^M - 1\) 标号。现在，\(N\) 个小朋友要在这个环上做游戏。每个小朋友一开始都占据了一个位置，之后，每隔一秒，每个小朋友都会沿顺时针移动到下一个位置上，求满足小朋友们所占据位置的编号的异或和为 \(S\) 的时刻个数。
题解
每个数都加上相同的数，要求异或和，计数。这些约束可以让我们想到数位 DP。
套路地，令 \(f_{i,j,0/1}\) 表示只考虑低 \(i\) 为，\(i\) 位向 \(i+1\) 位进位为 \(j\)，是否超过边界的方案数。
我们需要干两个事情：计算当前位异或和，计算当前位向下一位的进位。
我们需要观察到一个关键性质：进位为 \(j\) 说明只考虑低 \(i\) 位，前 \(j\) 大的数各进一位。
然后我们维护的信息类似于：前 \(i-1\) 位前 \(j\) 大中，第 \(i\) 位为 \(1\) 的数字个数。这个可以通过基数排序维护。
从高到低应该也能做。
提交记录
P3647 [APIO2014] 连珠线 紫
题意
有一个游戏称为连珠线。线是红色或蓝色的，珠子被编号为 \(1\) 到 \(n\)。这个游戏从一个珠子开始，每次会用如下方式添加一个新的珠子：
Append(w, v)：一个新的珠子 \(w\) 和一个已经添加的珠子 \(v\) 用红线连接起来。
Insert(w, u, v)：一个新的珠子 \(w\) 插入到用红线连起来的两个珠子 \(u, v\) 之间。具体过程是删去 \(u, v\) 之间红线，分别用蓝线连接 \(u, w\) 和 \(w, v\)。
给定一棵树，请对这棵树的边进行红蓝染色，满足这棵树是一个可能被得到的游戏局面，并且蓝边的权值和被最大化。输出蓝边权值和的最大值。
题解
以一开始的珠子为根，如果一颗红链之后变成了蓝链，那么可以视为一开始就加入了这条蓝链。我们发现我们每次会在树上加入一个长度为 \(1\) 的红链或长度为 \(2\) 的根向蓝链。
如果已知开始的珠子，我们只需要树形 DP 出若干根向长度为 \(2\) 的不交路径最大权值和。
但是我们不知道开始的珠子，所以换根 DP 就行了。
提交记录
CF1773G Game of Questions *2800
题意
Genie 正在参加一个问答比赛。比赛共 \(n\) 题，有 \(m\) 个参赛者（Genie 为 \(1\) 号参赛者）。
比赛的形式如下：先将 \(n\) 道题随机排序（即每个排列出现的概率都是 \(\dfrac{1}{n!}\)），然后按排列的顺序会依次问出这 \(n\) 个问题。问一个问题时，若所有人都会或所有人都不会则无事发生，否则不会的人会被淘汰。在 \(n\) 个问题都被问完之后，未被淘汰的人就都赢得胜利。
现在给出每个人是否会每道题，请求出 Genie 获胜的概率。
题解
首先需要注意到一个关键性质：重复是无关紧要的，因为重复的题目不会对场上的局面造成任何改变。
然后把问题转化成每次随机选题，令 \(f_S\) 表示场上剩余 \(S\) 时 \(1\) 的获胜概率，进行传统的概率 DP 即可。
在 DP 的时候需要处理 \(g_{S,T}\) 表示可以把场上的人从 \(S\) 淘汰到 \(T\) 的题目数量。
类比组合数，随便取一个不在 \(S\) 里面的数 \(x\)，有转移式 \(g_{S,T}=g_{S\cup x,T}+g_{S\cup x,T\cup x}\)。
卡常，需避免使用 umap 之类的工具，精细实现 \(g\) 的转移。
提交记录
CF908G New Year and Original Order *2800
题意
Let $ S(n) $ denote the number that represents the digits of $ n $ in sorted order. For example, $ S(1)=1,S(5)=5,S(50394)=3459,S(353535)=333555$ .
Given a number $ X $ , compute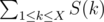 
modulo $ 10^{9}+7 $。
题解
横竖拆贡献，对于每个数码 \(x\ (1\leq x\leq 9)\)，\(x\) 对数字 \(k\) 的贡献计算方式如下：
- 记 \(k\) 中不小于 \(x\) 的数位个数为 \(t\)，贡献为 \(\sum\limits_{i=0}^{t-1}10^i\)，即 \(\underbrace{11\dots 1}_{t 个 1}\)。
枚举数码 \(x\)，数位 DP。
提交记录
CF1765C Card Guessing *2600
题意
考虑一副扑克牌。每张牌有 \(4\) 种花色，每种花色恰好有 \(n\) 张牌——因此，这副牌共有 \(4n\) 张牌。牌堆经过随机洗牌后，$ (4n)! $ 种可能的排列顺序每种都等概率出现。记 \(c_i\) 为牌堆中的第 \(i\) 张牌（从上到下编号）。
Monocarp 开始依次从牌堆顶抽牌。在抽每一张牌之前，他会尝试猜测这张牌的花色。Monocarp 会记住最近 \(k\) 张牌的花色，他的猜测是：在最近抽出的 \(k\) 张牌中出现次数最少的花色。也就是说，在抽第 \(i\) 张牌时，Monocarp 会猜测其花色为 \(c_{i-k}, c_{i-k+1}, \dots, c_{i-1}\) 这 \(k\) 张牌（如果 \(i \le k\)，则他会考虑所有已经抽出的牌，即 \(c_1, c_2, \dots, c_{i-1}\)）中出现次数最少的花色。如果有多个花色出现次数同为最少，他会等概率地随机选择其中之一作为猜测。
做出猜测后，Monocarp 抽出一张牌，并将其花色与自己的猜测进行比较。如果猜对了，则本次猜测正确；否则为错误。
你的任务是计算，Monocarp 抽完全部 \(4n\) 张牌后，猜对的次数的期望值。
题解
答案是每个位置猜对的概率之和。
对于一个位置，考虑卡牌怎么放置才能被猜中，当前牌需要在前 \(c=\min(i-1,k)\) 张牌中出现次数最小，组合数刻画这个方案数，然后跑一遍物品个数为 \(4\) 的 背包计算总和即可。
提交记录
AT_agc013_e Placing Squares 紫
题意
给长度为 \(n\ (n\leq 10^9)\) 的序列分段，一种方案的贡献为所有段长度的平方之积，给定 \(m\) 个地方不能作为断点，求所有方案贡献总和。
题解
将平方转化为组合意义：在区间内放置两个不同的球的方案数。
然后令 \(f_{i,0/1/2}\) 表示当前区间放了 \(0/1/2\) 个球的方案数，就可以分段矩阵乘法了。
提交记录
AT_agc030_f Permutation and Minimum 黑
题意
有一个 \(2N\) 个数的序列 \(A\)，从 1 到 \(2N\) 标号。你要把 \(1\sim 2N\) 这些数填进去，使它形成一个排列。
但是已经有一些位置强制填了特定的数了，输入时会给出。
最后令长度为 \(N\) 的序列 \(B\) 为：令 \(B_i=min\{A_{2i−1},A_{2i}\}\)。
询问所有方案中能得到的不同的 \(B\) 的数量。
\(N\leq 300\)。
题解
先把确定的位置扔掉，留下一边确定和两边都不确定的位置。
然后问题转化为将数字两两匹配，然后乘上两边都不确定位置数的阶乘来分配位置。
令 \(f_{i,j,k}\) 表示已填入 \(i\sim 2\times n\) 个数字，有 \(j\) 个不定位置的数字等待匹配，\(k\) 个确定位置的数字等待匹配。
转移时分：匹配一个位置确定的数、匹配一个位置不定的数、等待匹配三种情况讨论。
注意：位置确定的数不能互相匹配，匹配一个位置确定的数需要乘系数，因为不同位置的数显然不同。
从大到小填数的好处在于我们所填的数一但匹配，那么这个位置就确定了，不会算重。
提交记录
[ABC262Ex] Max Limited Sequence 黑
题意
求满足以下条件的长度为 \(N\) 的序列 \(A=(A_1,A_2,\cdots A_N)\) 有多少种：
- \(\forall i \in[1,N],0\leq A_i\leq M\)
- \(\forall i \in[1,Q],\max \limits_{L_i\leq j\leq R_i}A_j=X_i\)
\(N\leq 2\times 10^5\)。
题解
容易得出每个数的上界，且可以发现我们只关心每个数是否取到上界。
然后上限低的位置不会对上限高的位置和限制高的区间造成任何影响，因此上限不同的位置是独立的。
因此我们现在只需要解决 \(X\) 都相同的情况，令 \(f_{i,j}\) 表示前 \(i\) 个位置，上一个取到最大值的位置是 \(j\) 的方案数，线段树维护整体 DP 即可（转移比较特殊，也可以不用线段树）。
细节还挺多的。
提交记录
CF53E Dead Ends *2500
题意
求一张图有 \(k\) 个叶子的生成树数量。
\(n\leq 10,m\leq \binom{n}{2}\)。
题解
状压 DP，以 \(1\) 为根一层层加入节点，令 \(dp_{x,S,T}\) 表示树上节点集合是 \(S\)，最后一层节点是 \(T\)，除 \(T\) 以外有 \(x\) 个叶子。这里“除 \(T\) 以外”是因为 \(T\) 中的点还不确定是否是叶子。
转移时枚举一个 \(S\) 补集的子集将其每个节点连向 \(T\)，假设 \(T\) 中有 \(x\) 个节点没有被连接，那么会增加 \(x\) 个叶子（注意如果 \(S=T=1\) 且加入的集合大小也为 \(1\)，那么要额外加上节点 \(1\) 这个叶子）。
我们枚举 \(x\)，然后需要处理 \(g_{S,T,x}\) 表示 \(S\) 中的节点向 \(T\) 中的节点连边，且 \(T\) 中有 \(x\) 个节点被至少一个点连边的方案数。这部分可以做到 \(O(n2^n\times n2^n)=O(n^2 4^n)\)。
那么我们可以令 \(to_{S,T}\) 表示 \(S\) 中的节点向 \(T\) 中的节点连边，不做任何要求的方案数，\(to\) 可以直接把每个点的方案数乘起来，然后容斥一下可以得到 \(g_{S,T,|T|}\)。
则有 \(g_{S,T,x}=\sum\limits_{T'\subseteq T\land \operatorname{popcnt}(T')=x} g_{S,T',|T'|}\)，这部分可以做到 \(O(2^n\times 3^n)=O(6^n)\)。
有了 \(g\) 可以轻松得到 \(dp\) 的转移。
时间复杂度 \(O(6^n+n^2 4^n)\)。
提交记录
CF1789F Serval and Brain Power *2700
题意
定义一个字符串 \(T\) 是好的，当且仅当存在字符串 \(T'\) 和整数 \(k(k\geq2)\)，使得 \(T\) 可以由 \(k\) 个 \(T'\) 首尾相接得到。
例如，字符串 \(\texttt{gogogo}\) 就是好的，因为它可以由 \(3\) 个字符串 \(\texttt{go}\) 首尾相接得到；而 \(\texttt{power}\) 就不是好的。
给定仅包含小写英文字母的字符串 \(S\)。求出 \(S\) 最长的好的子序列的长度。
\(|S|\leq 80\)。
题解
对于重复次数 \(\leq 3\) 的，直接枚举断点然后求 LCS。
对于重复次数 \(\geq 4\) 的，那么单位序列长度 \(\leq 20\)，直接枚举起点然后暴力，经过合理的剪枝可以做到 \(O(5\times 2^20\times n)\)。
提交记录
P12038 [USTCPC 2025] 送温暖 紫
题意
给定一个 \(n\) 个点的树，点 \(i\) 的点权为 \(a_i\)，你需要从中选出一个连通块，使得它们的点权和模 \(M\) 的余数最大。克露丝卡尔酱想知道这个点权和模 \(M\) 的余数最大是多少。
\(n\leq 33\)。
题解
找出重心，不包含重心的情况可以暴力。
然后把重心的若干子树平均分成两半 meet in the middle。
提交记录
CF1552G A Serious Referee *3000
题意
Andrea 想出了一个他认为新颖的长度为 \(n\) 的数组排序算法。该算法的工作方式如下：
最初有一个包含 \(n\) 个整数 \(a_1,\, a_2,\, \dots,\, a_n\) 的数组。然后，执行 \(k\) 步操作。
在第 \(i\) 步中，将子序列 \(a_{j_{i,1}},\, a_{j_{i,2}},\, \dots,\, a_{j_{i,q_i}}\) 排序，数组中的其他元素保持不变。
判断 Andrea 的算法是否正确，也就是说，对于任意长度为 \(n\) 的整数数组 \(a\)，算法结束后数组 \(a\) 是否一定有序。
题解
首先发现值域是无关紧要的，能对所有数组 \(a\) 排序当且仅当能被所有 \(01\) 序列排序。
直接枚举会炸，我们每次只枚举被排过序的地方，这样的好处是我们新增一个排序操作后，这个排序操作所对应的位置一定有序，而其余被排过序的位置一定不变。因此我们每次只需要枚举 \(0\) 的个数即可。
复杂度为将 \(n\) 分为 \(k\) 份，所有份乘积的最大值乘上 \(n\)，由于极限数据下 \(3k<n\)，因此复杂度为 \(O((\frac{n}{k})^kn)\)。
提交记录
CF1601F Two Sorts *3400
题意
将 \(1\) 到 \(n\)（包含）的整数按字典序排序（将整数视为字符串）。排序后得到数组 \(a_1, a_2, \dots, a_n\)。
计算 \((\sum_{i = 1}^n ((i - a_i) \mod 998244353)) \mod 10^9 + 7\) 的值。
\(n\leq 10^{12}\)。
题解
\(n\leq 10^{12}\) 提示我们使用折半算法。
考查 \(O(n)\) 的暴力过程，在字典树上暴力搜索，求 \(\sum ((dfn_i-i)\bmod 998244353)\bmod (10^9+7)\)，这启示我们可以求 \(a_i\) 的逆排列 \(b_i\)，然后求 \(\sum b_i-i\)，可以通过折半搜索 \(i\)，然后当高 \(6\) 位固定时 \(b_i\) 与低 \(6\) 位有一定规律，可以批量计算。
直接折半搜索有很多细节，令比如固定高位还是低位位数等，如果你固定低位位数为 \(6\)，那么你发现字典序排序可能出现形如下面的情况：
然后高位确定时低位不一定连续，然后做不下去了。
如果你固定高位位数为 \(6\)，那么你无法确定低位可以拼的位数，那么你的字典序排名也是不好求的，如果硬做，你会多若干个 \(\log\) 因子。
我们回归到在字典树上搜索的方法，仿照数位 DP 减少运算次数的方法，当子树内是深度为 \(6\) 的满字典树时，就可以直接借助预处理的东西直接算了。
具体的，令 \(dfn\) 为数值不超过 \(n\) 的字典树的 \(dfs\) 序，\(dfn'\) 表示在深度为 \(6\) 的满字典树的 \(dfs\) 序，我们在深度为 \(6\) 的满字典树上搜索并计算这棵树的 \(dfn'_i-i\) 集合。
假设我们在数值不超过 \(n\) 的字典树上搜到的数是 \(x\)，要往下接一个 \(t\) 位数的 \(y\)，那么这个拼接完的数的贡献就是 \(dfn_x-x\times 10^t+dfn'_y-y\)。
对于 \(0\sim 6\) 位分别开 vector 存下来，然后在数值不超过 \(n\) 的字典树上搜索，如果当前数字 \(x\) 满足 \(x\times B+B-1\leq n\land x\times B\times 10>n\) 则说明 \(x\) 子树下的分支是深度为 \(6\) 的满字典树，那么枚举往下接的位数，然后 vector 上二分算出有多少个数需要减去 \(998244353\) 即可。
提交记录
P3881 [JLOI2008] CODES 黑
题意
给定 \(n\) 个 \(\texttt{01}\) 编码串 \(S_1,S_2,\dots,S_n\)，你的任务是寻找一个编码串 \(T\)，使得它至少可以被划分为两种不同的 \(S_i\) 的排列。\(S\) 可以重复使用。
最小化 \(T\) 的长度并构造方案。
\(n\leq 20，len\leq 20\)。
题解
考虑双序列 DP，即模拟往两个序列中填数的过程。
令 \(f_{i,S}\) 表示已经填了 \(i\) 位，多出未匹配的字符串为 \(S\) 的最小 \(T\)，这样空间爆炸。
注意到我们每次往短的序列中加上一个字符串，那么我们多出的部分必定是某个字符串的后缀。
因此令 \(f_{i,j,k}\) 表示已经填了 \(i\) 位，其中第二个序列的后 \(k\) 位没有匹配且属于 \(s_j\) 的后 \(k\) 位的最小 \(T\)，暴力转移的复杂度是 \(O(n^4(状态数)\times n(转移数)\times n^2(chkmin))=O(n^7)\)。
注意到 \(i\) 只和转移顺序有关，因为我们已经在 \(f\) 中存了当前字符串。
换句话说我们删掉第 \(i\) 维唯一的坏处是不知道转移顺序。
因此直接滚掉第 \(i\) 维，使用 dijkstra 进行转移顺序不确定的 DP 即可。
提交记录
CodeChef-SADPAIRS Chef and Sad Pairs *2925
题意
给定一张图，每个点有一个颜色。
对于每个点求：
- 删去这个与点相连的所有边后，图上颜色相同且不可达的无序点对数量。
\(n,m\leq 2\times 10^5\)。
题解
建出圆方树，不同连通块之间的贡献是好算的，相同连通块贡献相当于对每个点求圆方树上删掉这个点后两侧相同颜色数，对于每个点是不好求的，但是可以对于每个颜色建立虚树，然后在虚树上统计，一个颜色对于其所对应虚树的相邻两个节点之间的所有点贡献一样，做一个树上差分即可。
提交记录
P10674 【MX-S1-T3】电动力学 紫
题意
给定一张包含 \(n\) 个点 \(m\) 条边的简单无向连通图，点的编号为 \(1\sim n\)。
你需要求出有多少集合对 \(S,T\sube \{1,2,\dots,n\}\)，满足对于任意的 \(i\in S\)，要么 \(i\) 也 \(\in T\)，要么存在 \(x,y\in T\)（\(x\neq y\)），满足存在一条从 \(x\) 到 \(y\) 的简单路径经过 \(i\)。
注意，集合对 \(S,T\) 可以为空集。
输出答案对 \(998244353\) 取模后的结果。
题解
由于点双满足任意两点路径并集都是全集，因此将 \(T\) 看作圆方树上选若干个圆点， 记这些圆点所构成的虚树为 \(Tr\)，那么 \(S\) 就是 \(Tr\) 上所有方点邻域构成集合的子集。
那么，记 \(Tr\) 上所有方点邻域构成集合的子集大小为 \(x\)，这个 \(T\) 的贡献就是 \(2^x\)。
对 \(T\) 进行 DP，套路的，我们让方点承担计算贡献的责任，圆点只负责计数。
一个天真的想法是我们令每个方点的权值为 \(2^{deg}\) 次方然后求选若干个点所构成虚树的权值乘积和。
但是这样会算重，因为一个点可能会被相邻的多个方点计算。
那么我们考虑让一个方点的权值为 \(2^{deg-1}\)，即只计入其儿子的贡献，然后如果虚树的根节点是圆点就再 \(\times 2\)，就不会算重了。
之后就是套路的虚树计数 DP，令 \(f_{u}\) 表示 \(u\) 只考虑子树内，如果子树内有点则钦定其虚树向上延申的方案数。当 \(u\) 是圆点时，有 \(f_{u}=2\times \prod f_v\)，表示 \(u\) 可选可不选；当 \(u\) 是方点时，\(f_u=1+2^{deg_u-1}\times ((\prod f_{v})-1)\)，表示 \(u\) 不能选，乘上 \(u\) 的权值 \(2^{deg_u-1}\)，注意要单独考虑什么都不选的情况。
计算答案时，枚举虚树的 \(\text{lca}\)，如果这个点是圆点，分类讨论这个点是否选，如果是方点就必须不选，但是此时需要乘上这个方点的 \(2^{deg}\)。注意当 \(u\) 不选且要求 \(\text{lca}=u\) 是，需要保证 \(u\) 必须至少两个子树内有东西，这个需要用总方案数减去空方案和只有一个子树有东西的方案数来计算。
提交记录
CF1054F Electric Scheme *2700
题意
二维平面上铺了一些电线。每个电线可以看作一条线段，一些是水平的，另一些是竖直
的。在这些电线的交点处会迸发火花（不妨假设水平电线和竖直电线各自内部不交）。
现在电线消失了，你只知道所有 \(n\) 个火花的位置。求原来最少有多少根电线，并构造一组方案。
\(1\leq n\leq 1000\)。
题解
每个火花处放一个极小的十字，这样一定有解。
将同行或同列的相邻火花连边，如果能连上那么答案就会减一。
如果有相交的边不能同时连接，因此将边视作点，建出冲突关系图，答案就是 \(2n-最大独立集大小\)。
注意到这是一个二分图，跑二分图最大独立集即可，构造方法是跑完最大匹配后在残量网络上 DFS，找出左侧搜到的点和右侧没搜到的点，这些点就是最大独立集。下面来说明这件事。
使用最小割刻画最大独立集，最小割问题是要最小化 \(\sum\limits_{(u_i\to v_i,w_i)} w_i x_{u_i}(1-x_{v_i})\)，并强制 \(x_S=1,x_T=0\)。最大独立集问题是要最小化 \(\sum -x_u+\sum\limits_{(u_i - v_i)} +\infin x_{u_i}x_{v_i}\)。
我们发现一个 \(x\) 同号一个 \(x\) 异号，下式无法变形到上式。
一般图最大独立集是 NP 问题，但是我们只需要处理二分图，我们将二分图右部点的 \(x\) 取反，即 \(x=1\) 代表它实际在 \(T\)，\(x=0\) 代表它实际在 \(S\)，然后最大独立集的式子可以变为如下形式，因为 \(x_S=1,x_T=0\)，该式可进一步转化。
根据这个式子连边，然后求出最小割，并在残量网络上搜出一个割的构造，由于我们刚才对右部点进行了取反，因此最终的独立集是左侧搜到的点和右侧没有搜到的点。
实际实现的时候在把中间的边权从 \(+\infin\) 改为 \(1\) 也是可以的，因为中间的边受两侧点的限制最多流 \(1\) 的流量。
提交记录
CF1416F Showing Off *3300
题意
给定一个 \(n\times m\) 的 LRDU 矩阵，除此之外，矩阵上每个格子还有⼀个正整数权值 \(a_{i,j}\)。
现在我们根据这些信息求出一个新矩阵 \(b\)，\(b_{i,j}\) 的值为：从 \((i,j)\) 出发开始沿着格子上写的方向走 \(10^{100}\) 步之后，经过至少一次的所有单元格的 \(a_{i,j}\) 值之和。
现在给出矩阵 \(b\)，请构造任意符合条件的字符矩形，以及 \(a\)。或者报告无解。字符矩形需满足所有边缘的方向不能指向矩形外。
\(1\leq n\times m\leq 10^5\)。
题解
我们发现如果一个点 \(u\) 旁边存在一个小于它的点 \(v\)，那么令点 \(u\) 方向指向 \(v\) 并令 \(a_u=b_u-b_v\) 即可。
我们发现如果一个点 \(u\) 旁边的所有点的 \(b\) 都大于 \(b_u\)，那么这个点往哪走都不行，因此无解。
如果两个点权值相同，那么这两个点可能在同一个环中。
特殊的，如果一个点 \(u\) 旁边不存在一个小于它的点，那么这个点必定在环中，称这样的点为“黑点”，其余点为“白点”。
注意到一个环拆成若干个二元环是不会更差的。
我们把可以在同一个环中的点连边，容易发现这构成一个二分图，我们的问题是求一个匹配方案，要求关键点都被匹配。
我们考虑求最大匹配，但是这样是错的，因为白点可能抢占黑点的匹配。
我们考虑尽可能满足白点，避免其抢占黑点匹配，使用若干个虚拟白点将两侧点的数量补到一致，然后在所有白点之间两两连边，然后跑最大匹配即可。如果存在完美匹配即有解。
让我们尝试说明这是对的：当不存在黑点都被匹配的方案时，我们只加入了白点和白点之间的边，新图也不会存在黑点都被匹配的方案，因此新图不存在最大匹配；当存在黑点都被匹配的方案时，在黑点都被匹配的情况下两侧肯定剩下数量相同的白点，那么将这些白点两两匹配后就是完美匹配，因此完美匹配存在。
白点之间两两连边在网络流中可以使用虚点优化建图。
提交记录
QOJ#3555. Chameleon's Love *????
题意
这是一道交互题。
- 共有 \(2n\) 只变色龙，其中 \(n\) 只性别为 \(X\)，另外 \(n\) 只性别为 \(Y\)。
- 每只变色龙有一个原色，原色取值范围为 \(1\sim n\)，满足：
- 同一性别内部，所有变色龙的原色互不相同。
- 每只变色龙恰好与一只异性变色龙的原色相同。
- 每只变色龙有一个恋慕对象，满足：
- 恋慕对象一定是异性；
- 一只变色龙与其恋慕对象的原色不同；
- 每个变色龙恰好喜欢一只变色龙，且恰好被一只变色龙喜欢。
- 初始时只知道 \(n\)，其余信息全部未知。
- 允许进行如下操作（最多 \(20000\) 次）：
- 选择一个变色龙集合 \(S\) 举办聚会。
- 对于每只参加聚会的变色龙：
- 如果其恋慕对象也参加了聚会，则其肤色变为恋慕对象的原色。
- 否则，肤色保持为自己的原色。
- 最终，你会得到聚会上肤色种类数。
- 目标：通过不超过 \(20000\) 次聚会，确定每只变色龙与哪只变色龙原色相同（即找出所有原色配对的变色龙对）。
- 数据范围：\(n \le 500\)。
部分分：
- 所有恋慕关系都是双向的。
- 允许 \(O(n^2)\) 次询问。
- 性别已知。
题解
考虑部分分一，发现双向恋慕关系在一起时会彼此互换颜色，对肤色数没有任何影响，因此直接二分即可。
因此，我们称两个点 \(a,b\) “有关”，当且仅当满足以下三条中任意一条：
- \(a\) 喜欢 \(b\) 且 \(b\) 不喜欢 \(a\)。
- \(b\) 喜欢 \(a\) 且 \(a\) 不喜欢 \(b\)。
- \(a,b\) 原色相同。
注意我们完全忽略了双向喜欢的关系。
考虑部分分二，我们让变色龙两两聚会，如果颜色数是 \(1\) 就说明两个变色龙有关。
容易发现对于每个变色龙，与其有关的变色龙有 \(1\) 或 \(3\) 个。
如果与变色龙 \(x\) 有关的变色龙只有一个，设其为 \(y\)，那么有 \(x,y\) 原色相同，我们解决了变色龙 \(x\) 的问题。
否则，设 \(a\) 喜欢 \(x\)，\(x\) 与 \(b\) 原色相同，\(x\) 喜欢 \(c\)。我们选择 \(x\) 和 \(a,b,c\) 中的两个参加聚会，如果这两个人是 \(a,b\) 那么颜色数为 \(1\)，否则为 \(2\)，因此我们可以确定哪个是 \(c\)，求出所有变色龙的 \(c\) 后就可以推出与所有变色龙的 \(b\)。
考虑部分分三。
我们令每个 \(x\) 与一些性别与 \(x\) 不同的变色龙聚会，那么肤色数 \(\neq 聚会人数\)，当且仅当里面有变色龙与 \(x\) 有关，因此分三段二分即可。
考虑正解，我们发现部分分三的做法中，不需要满足【与 \(x\) 聚会的变色龙性别都与 \(x\) 不同】，只需要满足【与 \(x\) 聚会的变色龙互相没有关系】即可。
那么增量维护，维护两个独立集 \(S1,S2\)，加入一条变色龙时在 \(S1,S2\) 上二分，之后得到与新加入变色龙有关的若干点，之后再重构独立集即可。
由于这是二分图，且 \(n\leq 500\)，因此重构独立集是简单的，直接黑白染色即可。
时间复杂度 \(O(n^2\log n)\)，询问次数 \(O(n\log n)\)。
二分时注意剪枝，不然会被卡询问次数。
提交记录
QOJ#7999. 拉丁方 / P10062 [SNOI2024] 拉丁方 黑
题意
给定一个 \(n \times n\) 的矩阵，其中左上角的 \(R \times C\) 的子矩阵已经填好。要求将矩阵补充完整，使得每行每列均为 \(1 \sim n\) 的排列。需要给出构造或判断无解。
\(1 \leq n \leq 500\)。
部分分：\(C = n\)。
题解
考虑部分分，我们建出数与列的二分图，发现这是一个二分图边染色问题，\(k\) 正则二分图边染色必定有解，因为根据 Hall 定理一定存在一组匹配，然后删去匹配后变为 \(k-1\) 正则二分图，可归纳证明。
因此对于 \(C\neq n\)，我们先填上面的数字，将拉丁方补成 \(C=n\)，只要能填出上面 \(R\times n\) 合法的解，那么下面一定有解。
对于上面 \(R\times n\) 的数字，相当于左部点为 \(n\)，右部点为 \(R\) 的二分图，要染成 \(n-C\) 种颜色，并且每条边都要被染色，每种颜色 \(R\) 个。我们发现如果存在一个点，其度数大于 \(n-C\)，那么说明染色不能办到，否则直接套用二分图边染色即可求解。
填完上面的数字后再用二分图边染色填下面的数字即可。
提交记录
QOJ#8602. Занулити пiдвiдрiзок(UkrainianOI D2T4) *????
题意
给定一个长度为 \(n\) 的数列 \(a_1, a_2, \cdots, a_n\)。
初始时变量 \(x=0\)，每一步可以进行以下两种操作之一：
- \(x \leftarrow x + 1\)
- 选择一个 \(1 \leq i \leq n\)，令 \(a_i \gets a_i \oplus x\)
\(q\) 次询问，每次给定区间 \([l, r]\)，求最少操作次数使得子数组 \(a[l:r]\) 中的所有元素变为 \(0\)。
\(1 \leq n, q \leq 2 \times 10^5\)，\(1 \leq a_i < 2^{60}\)，强制在线。
部分分：\(O(nq)\) 的解法。
题解
首先每个数只会被异或两次，记最后操作到的 \(x\) 为 \(mx\)，那么区间 \([l,r]\) 的答案为 \(r-l+1+(mx+\sum\limits_{i=l}^{r}[a_i>mx])=2(r-l+1)-(\sum\limits_{i=l}^{r}[a_i\leq mx]-mx)\)，我们要最大化后面减去的部分，令 \(cnt_i\) 表示区间中等于 \(i\) 的数字个数，求出 \(cnt_i-1\) 在 \(i\in [2^h,+\infin)\) 前缀和数组 \(p\)，记区间中 \(a\) 的二进制最高位为 \(2^h\)，需要满足 \(x\geq 2^h\)，那么答案为 \((r-l+1)+cnt+2^{h}-\max\limits_{mx\geq 2^h} p_{mx}\)，\(cnt\) 表示最高位是 \(2^h\) 的数的个数。
注意我们要忽略 \(2\) 的整数幂，因为它们总会被异或一次。
我们把 \(cnt_i-1\) 看成扩展 Hall 定理的形式，即 \(cnt_i\to |S|,1\to |N(S)|\)，我们构造二分图，左部点为 \(a\)，右部点为所有 \(\geq 2^h\) 的整数，左边每个 \(a\) 向右边每个比它小的数连边，那么根据扩展 Hall 定理，最小失配数就是 \(\max \{|S|-|N(S)|\}\)，即 \(\max\limits_{mx\geq 2^h} p_{mx}\)。最小失配数可以由最大匹配数得到。
对每个 \(h\) 单独拎出来 \(\text{highbit}=h\) 的 \(a\) 序列，我们要干的事情就是每次给定某个序列的某个区间，求最大匹配。
引理：一定存在一个最大匹配，使得将左侧被匹配的点从大到小排序后，这个被匹配的序列偏序所有其他的最大匹配。
证明：考虑两个不互相偏序的匹配 \(B,C\)，将所有匹配边画出，图中将形成若干链和环，然后在这张图上构造新的匹配。对于链，由于是最大匹配，因此匹配方法唯一；对于环，让字典序更优，在新图中一定能找到一个不劣于 \(B,C\) 的匹配。
对序列扫描线，需要维护单点加入，并尝试增广掉最早被加入的节点，求最大匹配。这对于一般二分图是不能低于 \(O(n^2)\) 的。
考虑反向 Hall 定理，维护被匹配的集合 \(S\)，并求出只考虑 \(S\) 的 \(cnt_i-1\) 的前缀和，如果有位置大于 \(0\) 就会失配，即 \(S\) 是非法的。
新加入一个数 \(a_x\)，线段树维护 \(cnt_i-1\) 的前缀和，将 \([a_x,\max a]\) 加 \(1\)，如果出现 \(>0\) 的位置，找出最前 \(>0\) 的位置 \(p\)，并找到满足 \(a_y\in [2^h,p]\) 的最小 \(y\)，删掉 \(a_y\) 即可。
加入一个数 \(a_x\) 时，相当于在扫描线线段树上的 \(l\leq x\) 的答案加 \(1\)，删除同理。由于强制在线，需要可持久化。
【2025/8/27 23:04】 没调完，睡觉了。
”注意我们要忽略 \(2\) 的整数幂，因为它们总会被异或一次。“的另一个原因是，我们需要让 \(cnt-1\) 的前缀最大值从 \(2^h+1\) 开始，先将 \(x\) 加到 \(2^h\)。
如果从 \(2^h\) 开始，那么实际上 \(x\) 被加到的初值是 \(2^h-1\)，那么此时如果存在完美匹配，无法判断 \(x\) 在这个方案中是否被加到了 \(2^h\) 及以上，如果没有则不符合题意，这会导致你的答案可能比正确答案少 \(1\)。
【2025/8/28 15:07】 调完了。
提交记录
——打造C++ IDE 续)
