题面:(粘自洛谷)
CF1864G Magic Square
题目描述
Aquamoon 有一个魔方,可以看作一个 \(n \times n\) 矩阵,矩阵的元素构成数字的排列 $1, \ldots, n^2 $ 。
Aquamoon 可以对矩阵执行两种操作:
- 行移位,即将矩阵的整行向右移动几个位置(至少 $ 1 $ 且最多 $ n-1 $ )。 超出矩阵右边界的元素将移至行的开头。 例如,将行 $ \begin{pmatrix} a & b & c \end{pmatrix} $ 移动 $ 2 $ 位置将导致 $ \begin{pmatrix} b & c & a \end{pmatrix} $ ;
- 列移位,即将矩阵的整列向下移动几个位置(至少 $ 1 $ 且最多 $ n-1 $ )。 来自矩阵下边界的元素被移动到列的开头。 例如,将列 $ \begin{pmatrix} a & b & c \end{pmatrix} $ 移动 $ 2 $ 个位置将导致 $ \begin{pmatrix} b & c & a \end{pmatrix} $ .
行从上到下编号为\(1\)到\(n\),列从左到右编号为\(1\)到\(n\)。 第 $ x $ 行和第 $ y $ 列交叉处的单元格表示为 $ (x, y) $ 。
Aquamoon 可以执行多项(可能是零)操作,但她必须遵守以下限制:
- 每行、每列最多可以移动一次;
- 矩阵的每个整数最多可以移动两次;
- 任意两个整数移动两次后的偏移量不能相同。 形式上,如果整数 $ a $ 和 $ b $ 被移动了两次,假设 $ a $ 已将其位置从 $ (x_1,y_1) $ 更改为 $ (x_2,y_2) $ ,并且 $ b $ 已将其位置从 $ (x_3,y_3) $ 到 $ (x_4,y_4) $ ,然后 $ x_2-x_1 \not\equiv x_4-x_3 \pmod{n} $ 或 $ y_2-y_1 \not\equiv y_4-y_3 \pmod{n } $ .
Aquamoon 想知道她可以通过多少种方式将魔方从给定的初始状态转变为给定的目标状态。 如果应用操作的顺序不同,则认为两种方式不同。 由于答案可能非常大,因此输出对 $ 998,244,353 $ 取模的结果。
输入格式
每个测试包含多个测试用例。 第一行包含测试用例的数量 $ t $ ( $ 1 \le t \le 2\cdot 10^4 $ )。 测试用例的描述如下。
每个测试用例的第一行包含一个整数 $ n $ ( $ 3\le n \le 500 $ )。
接下来的 $ n $ 行的第 $ i $ 行包含 $ n $ 个整数 $ a_{i1}, \ldots, a_{in} $ ,表示初始矩阵的第 $ i $ 行 ( $ 1 \le a_{ij} \le n^2 $ )。
接下来的 $ n $ 行中的第 $ i $ 行包含 $ n $ 个整数 $ b_{i1}, \ldots, b_{in} $ ,表示目标矩阵的第 $ i $ 行( $ 1 \le b_{ij} \le n^2 $ )。
保证初始矩阵的元素和目标矩阵的元素都构成数字的排列 $ 1, \ldots, n^2 $ 。
保证所有测试用例的\(n^2\)总和不超过\(250\,000\)。
输出格式
对于每个测试用例,如果可以在尊重所有限制的情况下将初始状态转换为目标状态,则输出一个整数 - 执行此操作的方法数,以 $ 998,244,353 $ 为模。
如果没有解决方案,则打印单个整数 $ 0 $ 。
输入输出样例
输入
4
3
1 2 3
4 5 6
7 8 9
7 2 3
1 4 5
6 8 9
3
1 2 3
4 5 6
7 8 9
3 2 1
6 5 4
9 7 8
3
1 2 3
4 5 6
7 8 9
7 8 1
2 3 4
5 6 9
3
1 2 3
4 5 6
7 8 9
3 8 4
5 1 9
7 6 2
输出
1
0
0
4
说明/提示
在第一个测试用例中,将初始矩阵转换为目标矩阵的唯一方法是将第二行向右移动 \(1\) 位置,然后将第一列向下移动 \(1\) 位置。
在第二个测试用例中,可以表明没有正确的方法来变换矩阵,因此,答案是 $ 0 $ 。
思路:
借鉴自Alex_Wei
因为一个数至多被操作两次,且每行每列至多被操作一次,所以一个数所在行经历过操作以后,这个数一定在正确的列上。同理,一个数所在列经历过操作以后,这个数一定在正确的行上。可以考虑反证法,我们假设起点经过行移动后到达了青色的点。显然,从青色的点到终点需要两步,此时该点移动了三步,与题意不符,故不成立。列操作同理可得。

此外,题目要求被操作的两个数的偏移向量不同,这里用一个\(vis\)数组就能解决。然而,我们可以将它作为条件推出一个很有用的性质:若至少有一行被操作,那每一列的偏移量不同;若至少有一列被操作,那每一行的偏移量不同。这个性质还是比较好推的,也是考虑反证:假设有两列的偏移量相同,然后再对任意一行的进行操作,那么一定有两个数的偏移向量一样,与题目相悖,故不存在。举个🌰,我们假设第\(i\)列和第\(j\)列同样向下偏移两个格,然后对第\(k\)行进行向右偏移的操作
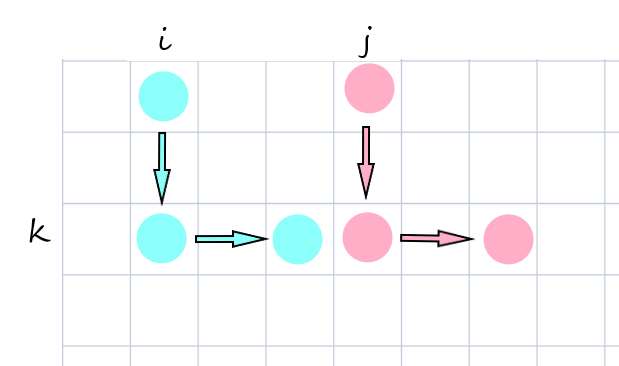
从图中,我们不难发现青点和粉点的偏移向量是一样的。
我们设第\(i\)行的偏移量为\(r_i\),第\(j\)列的偏移量为\(c_j\),由上述性质可得,任意的\(r_i\)互不相同且\(c_j\)互不相同(\(r_i≠0\),\(c_j≠0\))。
接下来我们要求出所有的\(r_i\)和\(c_j\)。若第\(i\)行存在一个数,该数的行没有改变,那么显然\(r_i\)只能等于这个数的偏移量。若第\(i\)行的所有数的行都改变了,也就是\(c_{1\sim n}\)均不为0。又因为\(1≤c_j<n\),所以存在相同且不为0的\(c_j\),这又说明所有的行均不能被操作,否则与上述性质矛盾,因此\(r_i=0\)。反之同理。这说明每一行/列的偏移量为定值,不会随着操作而改变。
我们假设一行的状态为合法的,当且仅当它没有被操作过,且\(r_i>0\),且操作后的数都在正确的列上。同理可设得合法的列的状态。假设某一时刻合法的只有行和列中的一种(只有行合法或只有列合法),那么这些行/列操作是相互独立的。假设有\(x\)行/列合法,因为操作的先后不影响最后的答案,而题目又说如果应用操作的顺序不同,则认为两种方式不同。,所以贡献为\(x!\)(\(x\)种操作的全排列)
若第\(i\)行和第\(j\)列同时合法,那么考虑\(a_{i,j}\),如果先操作第\(i\)行,且第\(j+r_i\)列的偏移量可以使得\(a_{i,j}\)到达正确的位置,那么因为先操作第\(j\)列也可以让\(a_{i,j}\)到达正确的行,所以第\(j\)列和第\(j+r_i\)列的偏移量相同,矛盾。同理可得先操作第\(j\)列也会矛盾。举🌰说明一下,我们假设\(a_{i,j}\)要移到蓝色点所在的位置,因为此时的列与行均合法(上面假设的),所以此时的\(c_j=k-i\)。假设我们先移动第\(i\)行,此时该点到达了\((i,j+r_i)\)的位置,要将该点移到正确的位置,此时\(c_{j+r_i}=k-i\),此时的\(c_{j+r_i}\)与\(c_j\)相同,与题目条件相悖,故不存在。

综上,不存在行和列同时合法。考虑当前所有合法的行与列,显然一次行操作不会增多或减少合法行,所以一定是当前合法行全部操作完后产生若干合法列,再将若干合法列操作完后产生新的合法行,行列交替操作知道不会产生新的合法行与列。此时检查一下每个数是否到达它应该到达的位置,若是则根据乘法原理输出若干阶乘相乘后的答案,否则无解。
时间复杂度大于等于\(O(n^2)\),小于等于\(O(n^3)\)
代码:
$code$
#include<iostream>
#include<map>
#include<vector>
#define int long long//不开long long见_____
using namespace std;
const int N=520,mod=998244353;
int T,n,cnt,ans,a[N][N],b[N][N],r[N],c[N],fac[N];pair<int,int> pos[N*N];bool vis[N][N];
inline void work(){cin>>n;for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) cin>>a[i][j],vis[i][j]=0;//输入+多测清空 for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) cin>>b[i][j],pos[b[i][j]]={i,j};//输入+记录结果位置 for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){int dx=(pos[a[i][j]].first-i+n)%n;int dy=(pos[a[i][j]].second-j+n)%n;//偏移向量 if(dx&&dy){//只考虑移动两次的数 if(vis[dx][dy]){//有过相同的偏移向量 cout<<"0\n";return ;}vis[dx][dy]=1;//标记当前偏移向量 }}}for(int i=1;i<=n;i++){map<int,int> mp;for(int j=1;j<=n;j++) mp[b[i][j]]=j;//记录对应位置所在列 r[i]=-1;//初始化 for(int j=1;j<=n;j++){auto it=mp.find(a[i][j]);//查找a[i][j]出现的列 if(it==mp.end()) continue;//没找到 int flag=(it->second-j+n)%n;//a[i][j]出现的列 if(r[i]==-1) r[i]=flag;//没有移动过 标记为当前偏移量 else if(r[i]!=flag){//与前面偏移量冲突 cout<<"0\n";//输出无解 return ;}}if(r[i]==-1) r[i]=0;//不用偏移 }for(int j=1;j<=n;j++){map<int,int> mp;for(int i=1;i<=n;i++) mp[b[i][j]]=i;c[j]=-1;for(int i=1;i<=n;i++){auto it=mp.find(a[i][j]);if(it==mp.end()) continue;int flag=(it->second-i+n)%n;if(c[j]==-1) c[j]=flag;else if(c[j]!=flag){cout<<"0\n";return ;}}if(c[j]==-1) c[j]=0;}//同上述求r[i]的过程 int ans=1,cur=0,last=-1;while(1){int cnt=0;if(!cur){//行操作 for(int i=1;i<=n;i++){if(!r[i]) continue;//不用偏移 bool ban=0;for(int j=1;j<=n;j++) if((pos[a[i][j]].second-j+n)%n!=r[i]) ban=1;//判当前行是否合法 if(!ban){//若合法 cnt++;//记录合法的行的数量 int d[N];for(int j=1,p=r[i]+1;j<=n;j++){d[p]=a[i][j];if(++p>n) p-=n;}//按照题目模拟偏移操作 memcpy(a[i],d,sizeof(d));//把值赋回原数组 }} }else{//列操作 for(int j=1;j<=n;j++){if(!c[j]) continue;bool ban=0;for(int i=1;i<=n;i++) if((pos[a[i][j]].first-i+n)%n!=c[j]) ban=1;if(!ban){cnt++;int d[N];for(int i=1,p=c[j]+1;i<=n;i++){d[p]=a[i][j];if(++p>n) p-=n;}for(int i=1;i<=n;i++) a[i][j]=d[i];}}}//同上述行操作 if(!cnt&&!last) break;//没有合法的行与列了 last=cnt;cur^=1;//记录上一次答案 转换行与列 ans=(ans*fac[cnt])%mod;//答案为阶乘相乘 }bool f=1;for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) f&=(a[i][j]==b[i][j]);//是否都到达指定位置 if(!f) cout<<"0\n";//只要有没到的就为无解 else cout<<ans<<'\n';//否则输出答案
}
signed main(){ios::sync_with_stdio(false);fac[0]=1;for(int i=1;i<N;i++) fac[i]=(fac[i-1]*i)%mod;//预处理阶乘 cin>>T;while(T--) work();return 0;
}
下述内容与题目无关
$song$
你是 遥遥的路
山野大雾里的灯
我是孩童啊 走在你的眼眸
你是 明月清风
我是你照拂的梦
见与不见都一生 与你相拥
而我将 爱你所爱的人间
愿你所愿的笑颜
你的手我蹒跚在牵
请带我去明天
如果说 你曾苦过我的甜
我愿活成你的愿
愿不枉啊 愿勇往啊
这盛世每一天
你是 岁月长河
星火燃起的天空
我是仰望者 就把你唱成歌
你是 我之所来
也是我心之所归
世间所有路都将 与你相逢
而我将 爱你所爱的人间
愿你所愿的笑颜
你的手我蹒跚在牵
请带我去明天
如果说 你曾苦过我的甜
我愿活成你的愿
愿不枉啊 愿勇往啊
这盛世每一天
山河无恙 烟火寻常
可是你如愿的眺望
孩子们啊 安睡梦乡
像你深爱的那样
而我将 梦你所梦的团圆
愿你所愿的永远
走你所走的长路
这样的爱你啊
我也将 见你未见的世界
写你未写的诗篇
天边的月 心中的念
你永在我身边
与你相约 一生清澈
如你年轻的脸
$picture$


























 - 教程)
























