当前位置：首页 > news >正文

实验二系统响应及系统稳定性

news 来源：原创 2025/7/22 17:42:06

实验目的

（1）学会运用Matlab 求解离散时间系统的零状态响应；

（2）学会运用Matlab 求解离散时间系统的单位取样响应；

（3）学会运用Matlab 求解离散时间系统的卷积和。

实验原理及实例分析

1. 离散时间系统的响应

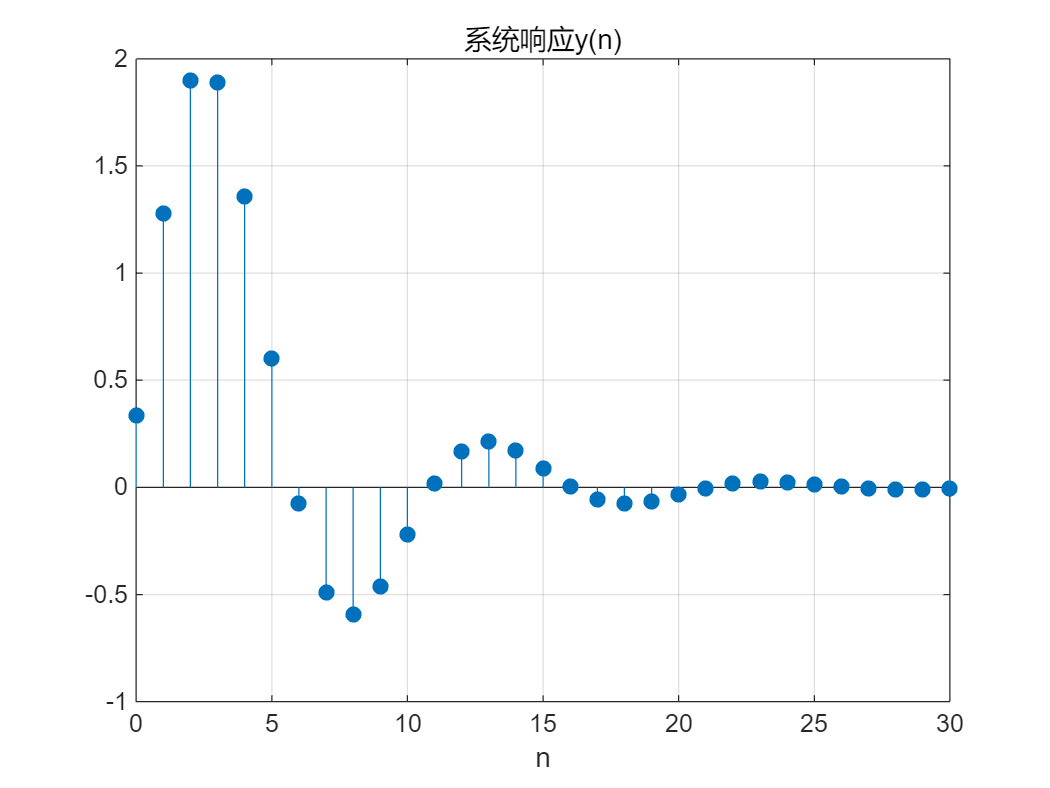
【例2-1】已知某LTI系统的差分方程为：

$3 y (n) - 4 y (n - 1) + 2 y (n - 2) = x (n) + 2 x (n - 1)$

试用Matlab命令绘出当激励信号为 $x(n)=(\frac{1}{2})^n u(n)$ 时该系统的零状态响应。

a=[3 -4 2];
b=[1 2];
n=0:30;
x=(1/2).^n;
%%%
% 函数名：filter(b,a,x)
% 功能：计算离散系统的零状态响应
% 格式：filter(b,a,x), 其中a 为响应的系数行向量，b 为激励的系数行向量,x 为激励序列。
y=filter(b,a,x);
%%%
stem(n,y,'filled'),grid on
xlabel('n'),title('系统响应y(n)')

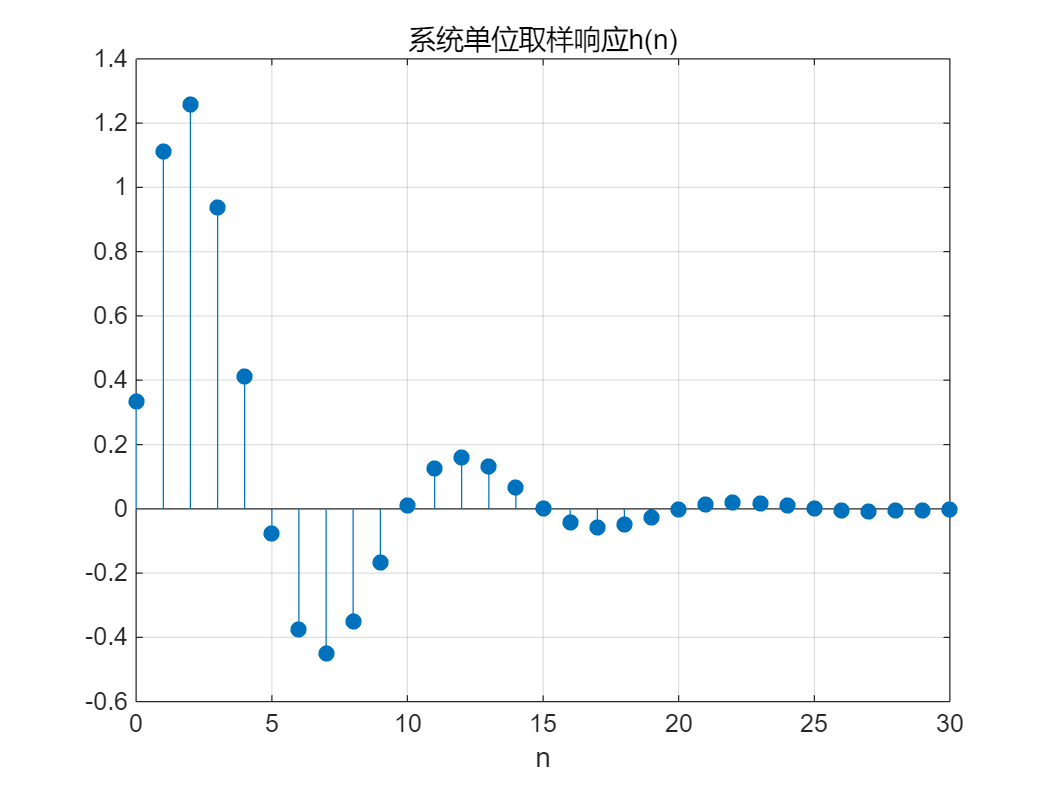
2. 离散时间系统的单位取样响应

系统的单位取样响应定义为系统在 $\delta (n)$ 激励下系统的零状态响应，用 $h (n)$ 表示。

Matlab 求解单位取样响应可利用函数filter，并将激励设为单位抽样序列。

例如，求解实例2-1 中系统的单位取样响应时，MATLAB 源程序为:

a=[3 -4 2];
b=[1 2];
n=0:30;
x=(n==0);% 产生单位抽样序列
h=filter(b,a,x);
stem(n,h,"fill"),grid on
xlabel('n'),title('系统单位取样响应h(n)')

Matlab另一种求单位取样响应的方法是利用控制系统工具箱提供的函数impz来实现。

a=[3 -4 2];
b=[1 2];
%%%
% 函数名：impz(b,a,N)
% 功能:求离散系统的单位响应并绘出图形
% 格式：其中，a 为响应的系数行向量，b 为激励的系数行向量，参数N通常为正整数，代表计算单位取样响应的样值个数。
impz(b,a,30);
%%%
grid on;
title('系统单位取样响应h(n)');

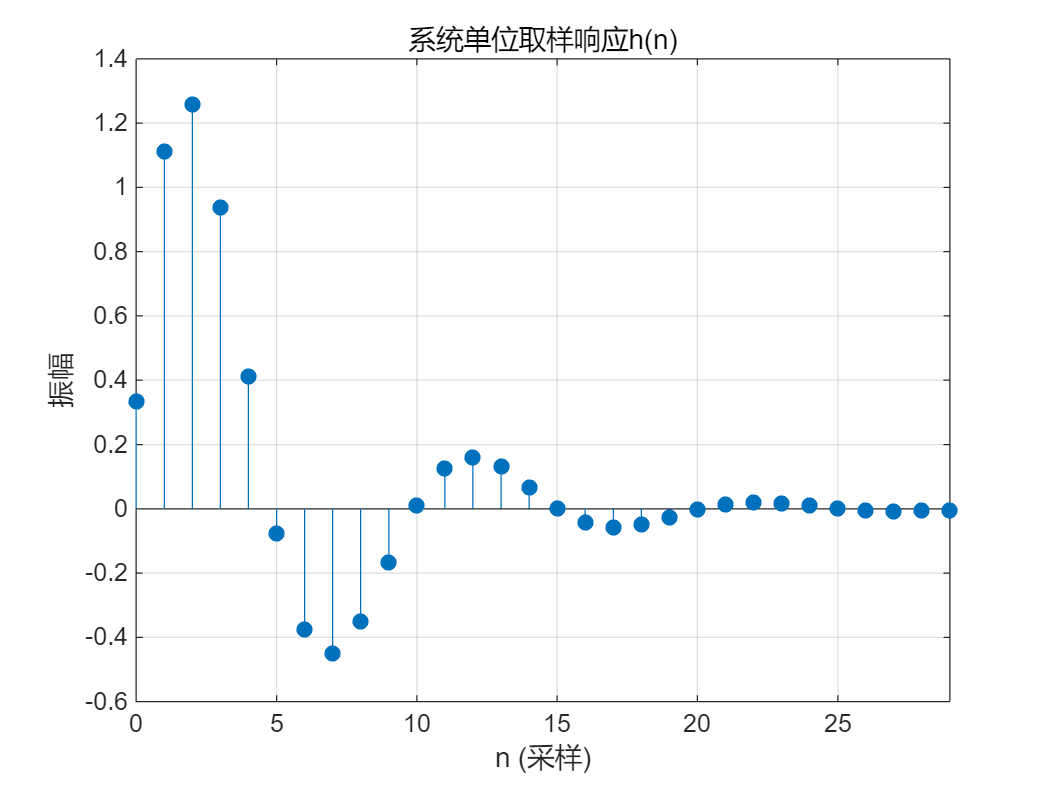
程序运行结果如图2-3 所示，比较图2-1 和图2-2，不难发现结果相同。

3. 离散时间信号的卷积和运算

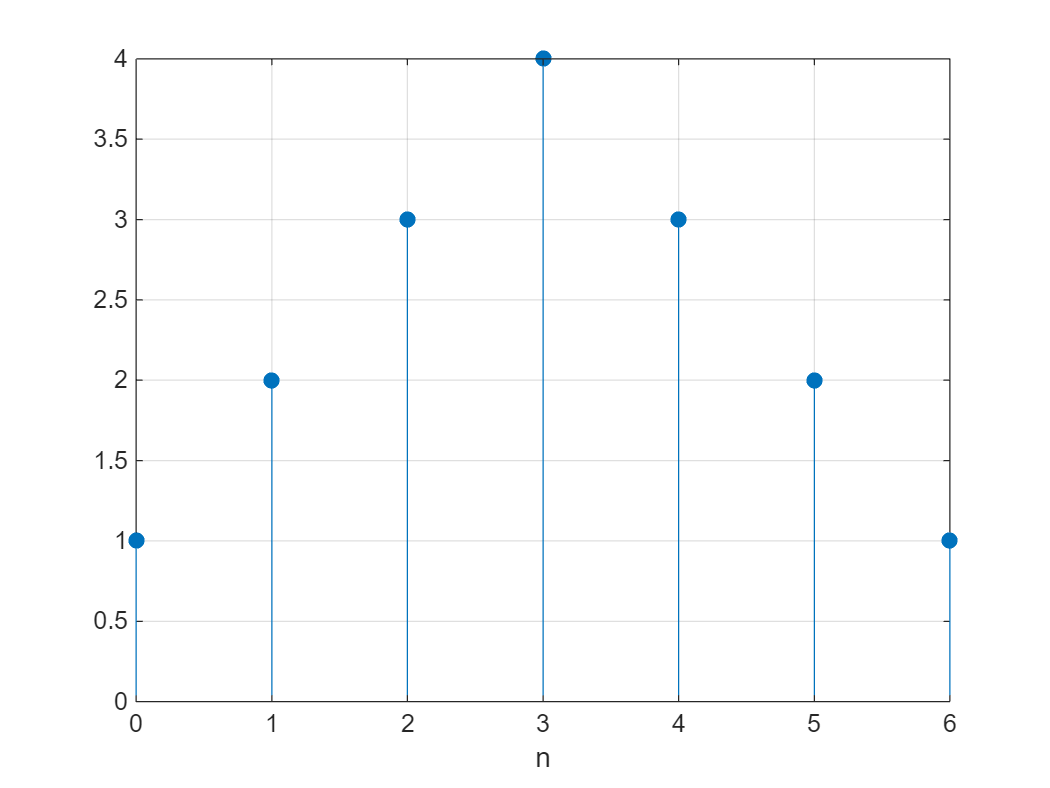
【例2-2】利用Matlab 的conv 命令求两个长为4 的矩形序列的卷积和。

即： $\textrm{g}\left(n\right)=\left\lbrack u\left(n\right)-u\left(n-4\right)\right\rbrack *\left\lbrack u\left(n\right)-u\left(n-4\right)\right\rbrack$

x1=ones(1,4);
x2=ones(1,4);
%%%
% 函数名f=conv(f1,f2)
% 功能：求卷积
% 格式：f1,f2 为参与卷积运算的两个序列，f 为卷积的结果，f 的长度为length(f1)+length(f2)-2
g=conv(x1,x2);
%%%
n=0:length(x1)+length(x2)-2;
stem(n,g,'filled'),grid on,xlabel('n')

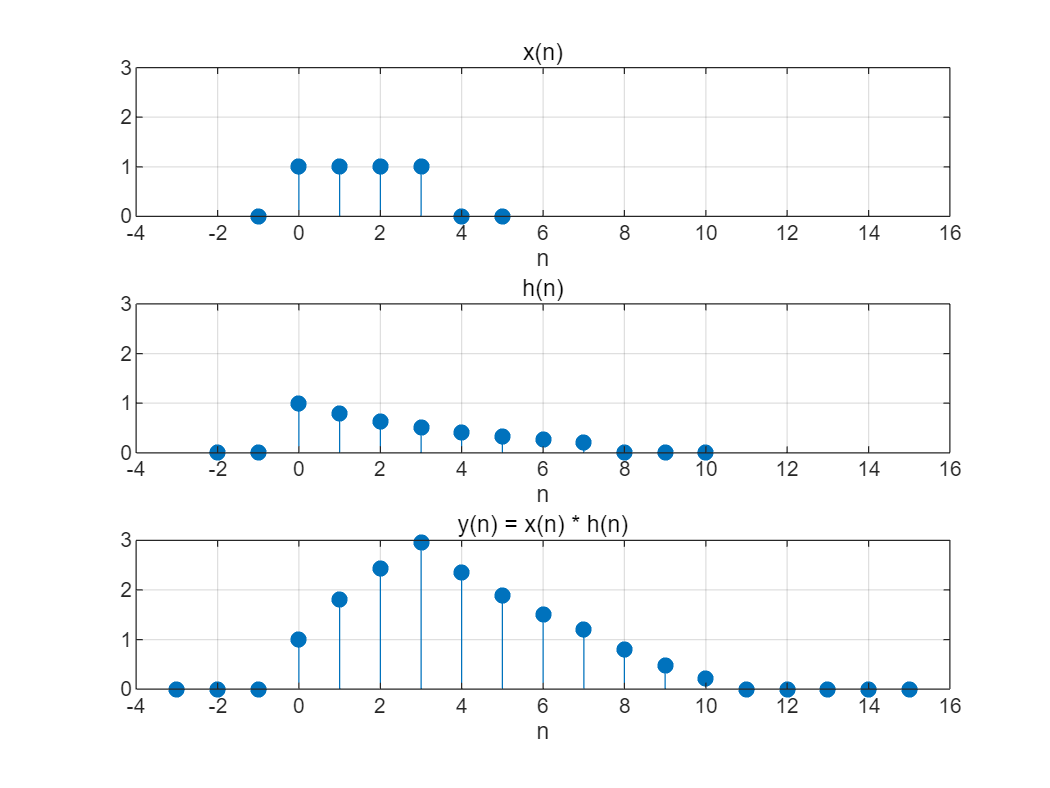
【例2-3】已知某系统的单位取样响应为 $h\left(n\right)=0.8^n \left\lbrack u\left(n\right)-u\left(n-8\right)\right\rbrack$ ，试求Matlab 求当激励信号为 $x\left(n\right)=u\left(n\right)-u\left(n-4\right)$ 时，系统的零状态响应。

解：Matlab 中可通过卷积求解零状态响应，即 $x\left(n\right)*h\left(n\right)$ 。由题意可知，

描述 $h\left(n\right)$ 向量的长度至少为 8，描述 $x\left(n\right)$ 向量的长度至少为 4，因此为了图形

完整美观，我们将 $h\left(n\right)$ 向量和 $x\left(n\right)$ 向量加上一些附加的零值。

addpath('.\2024-2025（1）《信号处理实验》资料（请拷贝到u盘中，每次试验带到实验室）\实验中用到的一些函数和音频图像文件');% 定义x(n)向量显示范围（添加了附加的零值）
nx = -1:5;
% 定义h(n)向量显示范围（添加了附加的零值）
nh = -2:10;% 生成单位阶跃序列
x = uDT(nx) - uDT(nx-4);
% 生成h(n)序列
h = 0.8.^nh .* (uDT(nh) - uDT(nh-8));% 计算卷积
y = conv(x, h);% 计算卷积结果的起始点和终点
ny1 = nx(1) + nh(1);
ny2 = nx(end) + nh(end);
ny = ny1:ny2;% 绘制x(n)的图像
subplot(311);
stem(nx, x, 'fill');
grid on;
xlabel('n');
title('x(n)');
axis([-4 16 0 3]);% 绘制h(n)的图像
subplot(312);
stem(nh, h, 'fill');
grid on;
xlabel('n');
title('h(n)');
axis([-4 16 0 3]);% 绘制y(n)的图像
subplot(313);
stem(ny, y, 'fill');
grid on;
xlabel('n');
title('y(n) = x(n) * h(n)');
axis([-4 16 0 3]);

实验内容

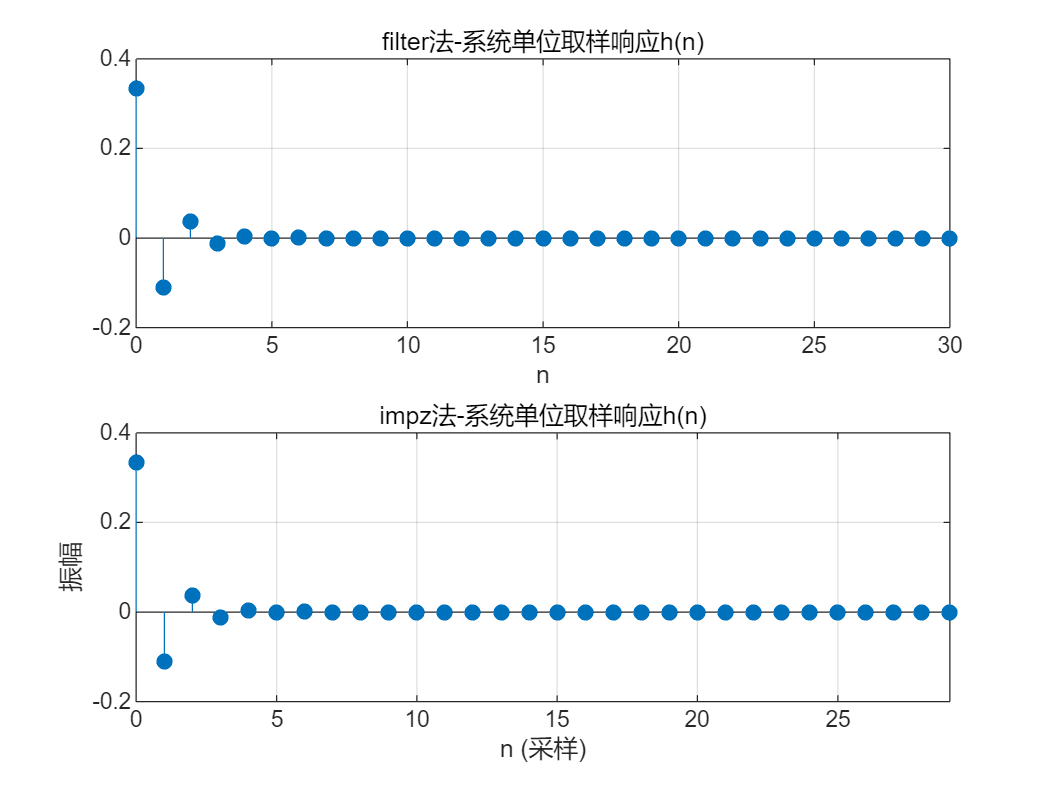
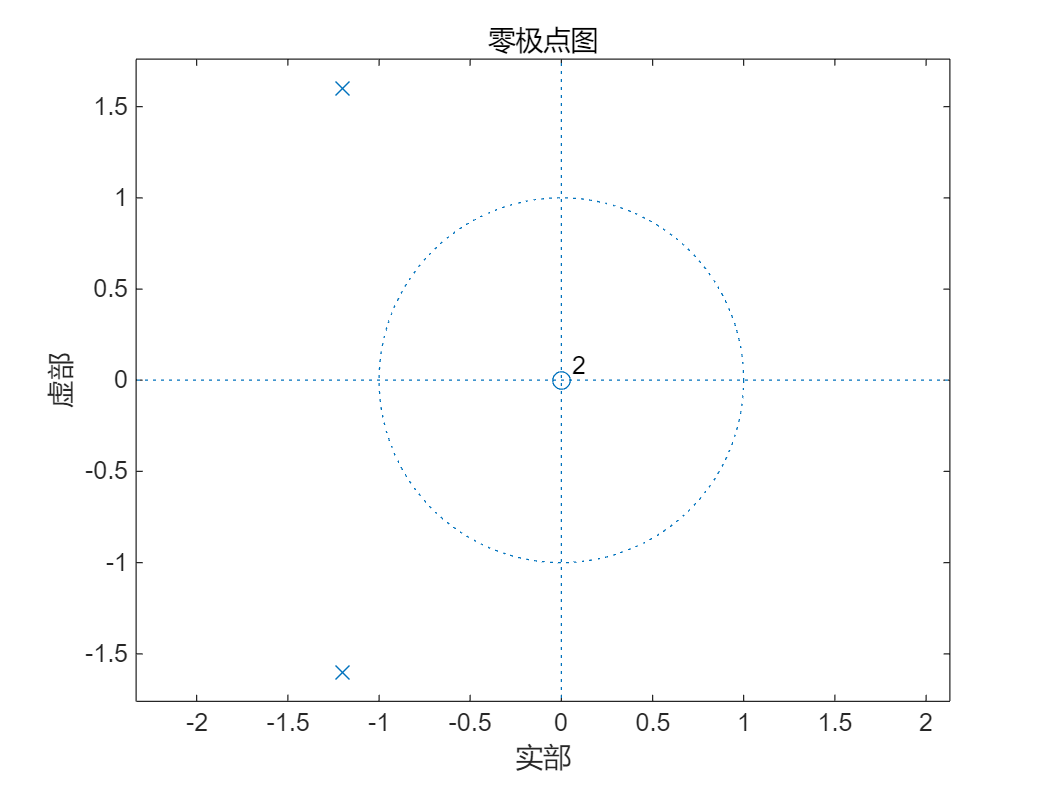
（1）试用Matlab 命令求解以下离散时间系统的单位取样响应，并判断系统的稳定性。

$ 1)~~3y\left(n\right)+4y\left(n-1\right)+y\left(n-2\right)=x\left(n\right)+x\left(n-1\right) $

clear;
clc;
close;a1=[3 4 1];
b1=[1 1];
n=0:30;
x=(n==0);% 产生单位抽样序列
h=filter(b1,a1,x);
subplot(211);
stem(n,h,"fill")
grid on
xlabel('n')
title('filter法-系统单位取样响应h(n)')subplot(212);
impz(b1,a1,30);
grid on;
title('impz法-系统单位取样响应h(n)');

%%%
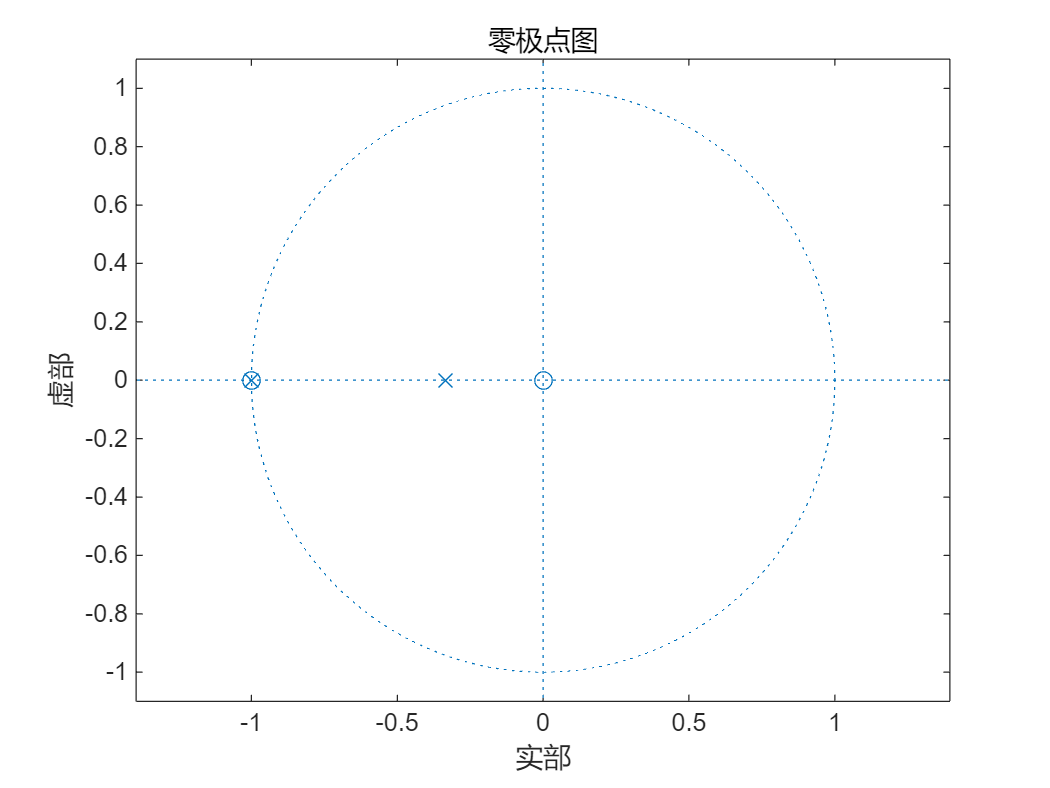
% 函数名：zplane(b,a)
% 功能：得到系统函数H(z)的零极点分布图
% 格式：其中b和a分别表示H(z)的分子和分母多项式的系数向量，函数的作用是在z平面上画出单位圆，零点和极点。
%%%
zplane(b1,a1);

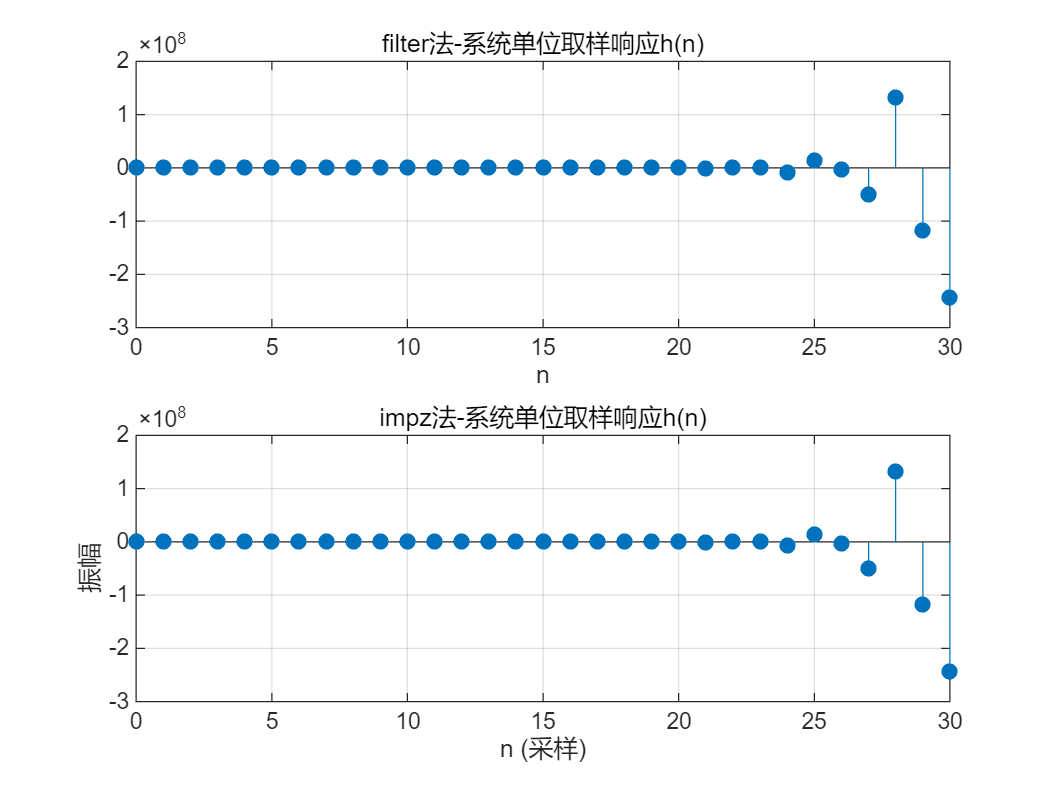
$ 2)~~\frac{5}{2}y\left(n\right)+6y\left(n-1\right)+10y\left(n-2\right)=x\left(n\right) $

close;
a2=[5/2 6 10];
b2=[1];
n=0:30;
x=(n==0);% 产生单位抽样序列
h=filter(b2,a2,x);
subplot(211)
stem(n,h,"fill")
grid on
xlabel('n')
title('filter法-系统单位取样响应h(n)')
subplot(212)
impz(b2,a2,31)
axis([0 30 -3*10^8 2*10^8]);
grid on
title('impz法-系统单位取样响应h(n)')

zplane(b2,a2);

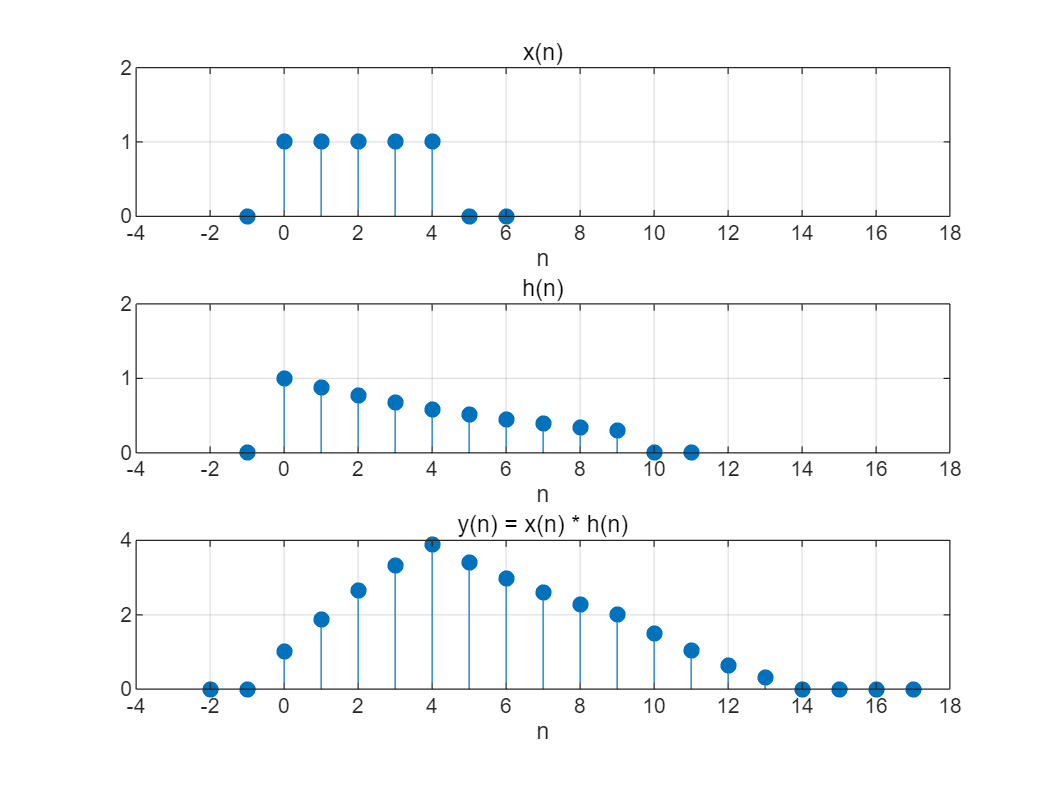
（2）已知某系统的单位取样响应为 $h\left(n\right)={\left(\frac{7}{8}\right)}^n \left\lbrack u\left(n\right)-u\left(n-10\right)\right\rbrack$ ，试用MATLAB 求当激励信号为 $x\left(n\right)=u\left(n\right)-u\left(n-5\right)$ 时，系统的零状态响应。

clear;
addpath('.\2024-2025（1）《信号处理实验》资料（请拷贝到u盘中，每次试验带到实验室）\实验中用到的一些函数和音频图像文件');
% 定义x(n)向量显示范围（添加了附加的零值）
nx = -1:6;
% 定义h(n)向量显示范围（添加了附加的零值）
nh = -1:11;% 生成单位阶跃序列
x = uDT(nx) - uDT(nx-5);
% 生成h(n)序列
h = (7/8).^nh .* (uDT(nh) - uDT(nh-10));% 计算卷积
y = conv(x, h);% 计算卷积结果的起始点和终点
ny1 = nx(1) + nh(1);
ny2 = nx(end) + nh(end);
ny = ny1:ny2;% 绘制x(n)的图像
subplot(311);
stem(nx, x, 'fill');
grid on;
xlabel('n');
title('x(n)');
axis([-4 18 0 2]);% 绘制h(n)的图像
subplot(312);
stem(nh, h, 'fill');
grid on;
xlabel('n');
title('h(n)');
axis([-4 18 0 2]);% 绘制y(n)的图像
subplot(313);
stem(ny, y, 'fill');
grid on;
xlabel('n');
title('y(n) = x(n) * h(n)');
axis([-4 18 0 4]);

（3）用数字图像处理中的Sobel 算子，调用conv2 函数对lena 图像进行滤波。

设两个3×3 的Sobel 矩阵算子Gx=[-1 0 1;-2 0 2;-1 0 1]，Gy=[1 2 1;0 0 0;-1-2 -1]。

读取lena 图像数据，保存到B 矩阵中；
分如下三种情况对B 进行卷积滤波

① 采用Gx 与B 进行卷积；

② 采用Gy 与的B 进行卷积；

③ 先采用Gx 与B 进行卷积，然后再采用Gy 与B 进行卷积；

④ 在一个figure 中，分四个子图显示出：原始图像，经过Gx 卷积滤波后

图像、经过Gy 卷积滤波后图像，先后采用Gx 和Gy 与的B 进行卷积滤波后

的图像，观察滤波后的图像的效果。

clear;
% 定义Sobel算子
Gx = [-1 0 1; -2 0 2; -1 0 1];
Gy = [1 2 1; 0 0 0; -1 -2 -1];% 读取Lena图像
B = imread('.\2024-2025（1）《信号处理实验》资料（请拷贝到u盘中，每次试验带到实验室）\实验中用到的一些函数和音频图像文件\lena.bmp')

B = 512x512 uint8 矩阵    131   136   133   132   137   137   135   138   133   134   132   128   128   129   126   122   122   120   118   116   113   108   103    99    84    86    77    74    71    67    68    60    59    57    52    56    67    67    62    65    70    73    67    64    70    71    72    79    73    74134   135   132   134   139   133   130   138   140   138   133   126   124   124   122   118   122   120   118   117   114   109   103    98    91    94    81    76    70    65    66    57    60    69    70    68    66    59    60    73    75    75    73    72    71    71    70    71    80    69136   129   137   134   130   135   132   133   135   130   127   128   131   131   126   121   121   114   116   115   108   107   102    90    89    84    78    84    70    69    60    57    55    54    56    60    56    67    59    65    68    72    77    76    69    65    71    80    74    76137   130   137   135   131   135   132   132   135   131   128   129   132   132   127   122   124   122   117   112   114   109   102    99   100    89    76    76    62    66    65    67    62    62    65    67    64    73    67    73    58    62    69    73    70    65    65    68    76    77137   132   137   135   131   134   133   132   135   132   129   129   132   132   128   124   127   125   116   110   115   108   105   103    97    89    79    81    67    69    64    64    56    57    62    62    59    66    62    69    66    66    69    74    75    73    73    75    75    71137   133   136   136   132   133   133   131   134   130   128   128   130   130   127   124   127   120   115   112   114   104   108   101    95    87    79    83    69    69    63    61    53    53    60    58    56    61    59    65    67    67    70    74    75    73    75    79    76    79136   134   134   136   132   131   134   130   131   128   126   126   128   128   126   124   124   120   115   114   120   103   108    99    90    85    79    83    70    69    61    58    62    60    68    65    66    68    67    72    63    68    77    82    80    74    74    78    65    66134   133   132   135   132   130   135   130   129   127   125   125   126   126   125   124   121   125   116   113   131   105   105   103    89    83    77    83    69    69    61    59    64    60    68    63    68    69    68    70    68    72    79    82    78    73    75    80    72    78132   132   130   134   131   129   136   130   129   127   126   125   126   127   126   126   120   125   114   111   132   102   105   103    96    86    75    76    63    67    66    68    60    53    60    55    64    65    63    62    71    70    70    71    69    66    68    73    76    74131   132   129   134   131   129   136   130   130   128   127   126   127   127   127   127   120   119   111   110   125    97   107   100    92    85    77    82    69    71    66    66    64    55    61    56    67    68    65    63    76    73    73    76    77    74    70    68    77    73


% ① 采用Gx与B进行卷积
B_Gx = conv2(B, Gx, 'same');% ② 采用Gy与B进行卷积
B_Gy = conv2(B, Gy, 'same');% ③ 先采用Gx与B进行卷积，然后再采用Gy与B进行卷积
B_Gx_Gy = conv2(B_Gx, Gy, 'same');% ④ 在一个figure中，分四个子图显示图像
figure;
subplot(2,2,1), imshow(B), title('原始图像');
subplot(2,2,2), imshow(B_Gx, []), title('Gx卷积滤波后图像');
subplot(2,2,3), imshow(B_Gy, []), title('Gy卷积滤波后图像');
subplot(2,2,4), imshow(B_Gx_Gy, []), title('Gx和Gy卷积滤波后图像');

原始图像：未经处理的灰度图像。

Gx卷积滤波后图像：突出水平边缘。

Gy卷积滤波后图像：突出垂直边缘。

Gx和Gy卷积滤波后图像：结合两者，全面突出边缘。

思考题

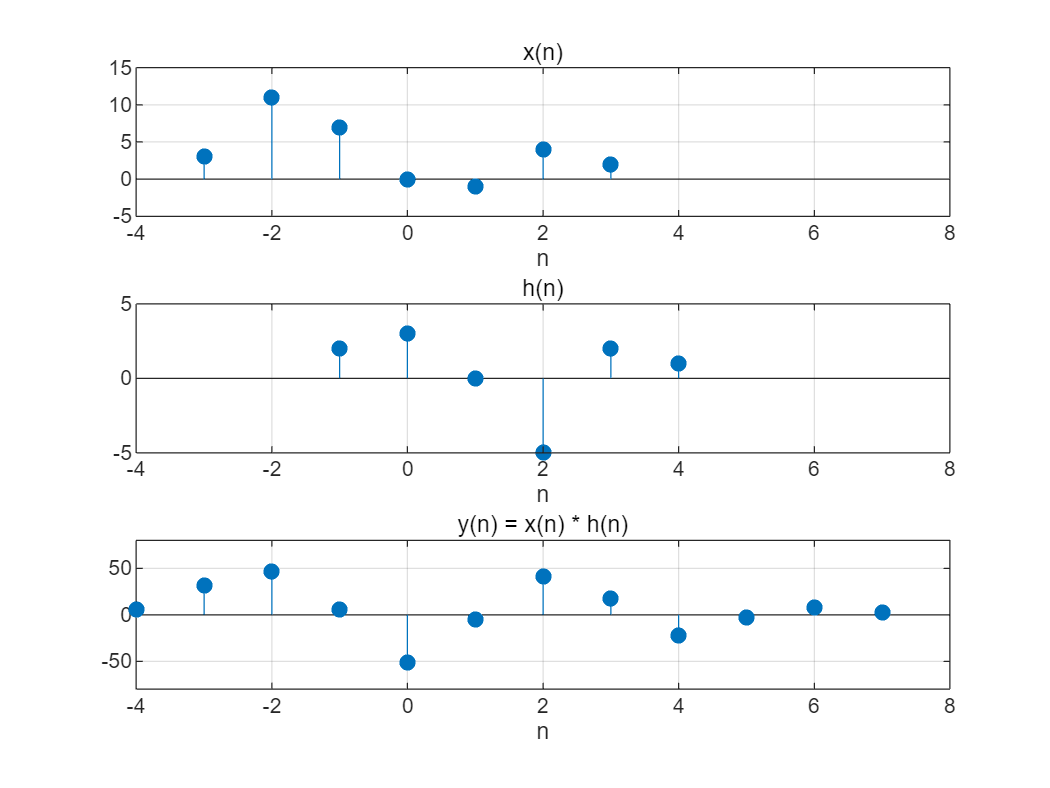
（1） Matlab 的工具箱函数conv，能用于计算两个有限长序列之间的卷积，但conv 函数假定这两个序列都从n=0 开始。试编写M 文件计算x(n) = [3,11,7,0,−1,4,2],−3≤ n ≤ 3 和 h(n) = [2,3,0,−5,2,1],−1≤ n ≤ 4 之间的卷积，并绘制y(n)的波形图。

close;
clear;
% 定义序列 x(n) 和 h(n)
nx = -3:3; % n 的范围
x = [3, 11, 7, 0, -1, 4, 2]; % x(n)nh = -1:4; % n 的范围
h = [2, 3, 0, -5, 2, 1]; % h(n)% 计算卷积
y = conv(x, h);% 定义 y(n) 的范围
ny = nx(1) + nh(1) : nx(end) + nh(end); % y(n) 的范围% 绘制x(n)的图像
subplot(311);
stem(nx, x, 'fill');
grid on;
xlabel('n');
title('x(n)');
axis([-4 8 -5 15]);% 绘制h(n)的图像
subplot(312);
stem(nh, h, 'fill');
grid on;
xlabel('n');
title('h(n)');
axis([-4 8 -5 5]);% 绘制y(n)的图像
subplot(313);
stem(ny, y, 'fill');
grid on;
xlabel('n');
title('y(n) = x(n) * h(n)');
axis([-4 8 -80 80]);

（2）在数字图像处理边缘检测技术中，除了Sobel 算子外，还有哪些边缘检测算子？通过查找资料，选择某种边缘检测算子，在Matlab 平台上编程实现对lena 或其他图像进行边缘检测，显示出原图和边缘检测后的图像。

Prewitt 算子
Canny 边缘检测
Roberts 交叉梯度算子
Laplacian 边缘检测
Scharr 算子

数字图像处理(19): 边缘检测算子(Roberts算子、Prewitt算子、Sobel算子和 Laplacian算子)_ubuntu写出roberts、sobel、laplace边缘检测算法-CSDN博客

图像特征与边缘检测：从Sobel算子到Canny边缘检测【计算机视觉】-CSDN博客

clear;
% 读取图像
img = imread([...'.\2024-2025（1）《信号处理实验》资料（请拷贝到u盘中，每次试验带到实验室）\实验中用到的一些函数和音频图像文件\lena_colour.bmp'% '运动.jpg'% '东方明珠.jpg']);
img_RGB = img; % MATLAB 读取图像默认是 RGB 格式% 灰度化处理图像
grayImage = rgb2gray(img);% 高斯滤波
gaussianBlur = imgaussfilt(grayImage, 1); % 1 为标准差% 阈值处理
binary = imbinarize(gaussianBlur, 0.5); % 0.5 为阈值% Roberts算子
kernelx = [-1 0; 0 1];
kernely = [0 -1; 1 0];
x_roberts = imfilter(double(binary), kernelx);
y_roberts = imfilter(double(binary), kernely);
Roberts = uint8(sqrt(x_roberts.^2 + y_roberts.^2));% Prewitt算子
kernelx = [1 1 1; 0 0 0; -1 -1 -1];
kernely = [-1 0 1; -1 0 1; -1 0 1];
x_prewitt = imfilter(double(binary), kernelx);
y_prewitt = imfilter(double(binary), kernely);
Prewitt = uint8(sqrt(x_prewitt.^2 + y_prewitt.^2));% Sobel算子
Sobel_x = imfilter(double(binary), fspecial('sobel'));
Sobel_y = imfilter(double(binary), fspecial('sobel')');
Sobel = uint8(sqrt(Sobel_x.^2 + Sobel_y.^2));% Laplacian算子
Laplacian = uint8(imfilter(double(binary), fspecial('laplacian')));% 显示图像
figure;
subplot(2, 3, 1), imshow(img_RGB), title('原始图像'), axis off;
subplot(2, 3, 2), imshow(binary,[]), title('二值图'), axis off;
subplot(2, 3, 3), imshow(Roberts,[]), title('Roberts算子'), axis off;
subplot(2, 3, 4), imshow(Prewitt,[]), title('Prewitt算子'), axis off;
subplot(2, 3, 5), imshow(Sobel,[]), title('Sobel算子'), axis off;
subplot(2, 3, 6), imshow(Laplacian,[]), title('Laplacian算子'), axis off;

clear;


% 读取图像
img = imread('.\2024-2025（1）《信号处理实验》资料（请拷贝到u盘中，每次试验带到实验室）\实验中用到的一些函数和音频图像文件\lena_colour.bmp');
img_RGB = img; % MATLAB 读取图像默认是 RGB 格式% 灰度化处理图像
grayImage = rgb2gray(img);% 高斯滤波
gaussianBlur = imgaussfilt(grayImage, 1); % 1 为标准差% 阈值处理
binary = imbinarize(gaussianBlur, 0.); % 0.5 为阈值% Roberts算子（使用 conv2）
kernelx = [-1 0; 0 1];
kernely = [0 -1; 1 0];
x_roberts = conv2(double(binary), kernelx, 'same');
y_roberts = conv2(double(binary), kernely, 'same');
Roberts = uint8(sqrt(x_roberts.^2 + y_roberts.^2));% Prewitt算子（使用 conv2）
kernelx_prewitt = [1 1 1; 0 0 0; -1 -1 -1];
kernely_prewitt = [-1 0 1; -1 0 1; -1 0 1];
x_prewitt = conv2(double(binary), kernelx_prewitt, 'same');
y_prewitt = conv2(double(binary), kernely_prewitt, 'same');
Prewitt = uint8(sqrt(x_prewitt.^2 + y_prewitt.^2));% Sobel算子（使用 conv2）
Sobel_x = conv2(double(binary), fspecial('sobel'), 'same');
Sobel_y = conv2(double(binary), fspecial('sobel')', 'same');
Sobel = uint8(sqrt(Sobel_x.^2 + Sobel_y.^2));% Laplacian算子（使用 conv2）
Laplacian = uint8(conv2(double(binary), fspecial('laplacian'), 'same'));% 显示图像
figure;
subplot(2, 3, 1), imshow(img_RGB), title('原始图像'), axis off;
subplot(2, 3, 2), imshow(binary, []), title('二值图'), axis off;
subplot(2, 3, 3), imshow(Roberts, []), title('Roberts算子'), axis off;
subplot(2, 3, 4), imshow(Prewitt, []), title('Prewitt算子'), axis off;
subplot(2, 3, 5), imshow(Sobel, []), title('Sobel算子'), axis off;
subplot(2, 3, 6), imshow(Laplacian, []), title('Laplacian算子'), axis off;