当前位置：首页 > news >正文

OpenXLSX开源库在 Ubuntu 18.04 的编译、交叉编译与使用教程

news 来源：原创 2025/6/19 6:10:43

😁博客主页😁：🚀https://blog.csdn.net/wkd_007🚀
🤑博客内容🤑：🍭嵌入式开发、Linux、C语言、C++、数据结构、音视频🍭
🤣本文内容🤣：🍭介绍 🍭
😎金句分享😎：🍭你不能选择最好的，但最好的会来选择你——泰戈尔🍭
⏰发布时间⏰：

本文未经允许，不得转发！！！

🎄一、概述

最近项目需要将日志写到.xlsx中，了解到C和C++的操作.xlsx几个开源库：
在这里插入图片描述
本文主要介绍OpenXLSX在Ubuntu 18.04 下的编译和使用。

在这里插入图片描述

🎄二、OpenXLSX 介绍

OpenXLSX是一款用于读取、写入、创建和修改Microsoft Excel®文件的C++库，支持.xlsx格式。经过一段长时间的沉寂后，作者于2024.05决定重启开发开放XLSX项目。代码已被彻底清理，并修复了大量错误。该库已在Windows、macOS及Linux上进行了测试，确保在所有平台上正常运行。

OpenXLSX在GitHub的开源地址：https://github.com/troldal/OpenXLSX

目前，OpenXLSX仅依赖以下第三方库：

PugiXML
Zippy（miniz的C++封装）
Boost.Nowide（用于在Windows平台打开非ASCII命名文件）

OpenXLSX采用CMake作为构建系统（确切地说是构建系统生成器)。

OpenXLSX的功能及状态
OpenXLSX 正处于研发阶段。以下列出的功能已实施并应正常运作：

创建/打开/保存文件
读取/写入/修改单元格内容
复制单元格与区域
复制工作表
单元格区域和迭代器
行范围及迭代器

至于格式化、图表和图像相关的功能尚未实现，短期内也暂无计划。

需特别说明的是，目前创建常量 XLDocument 对象的功能尚不支持！

压缩库
Excel文件本质上是一系列.xml文件打包在一个.zip存档中。OpenXLSX使用第三方库从.zip存档中提取.xml文件。默认使用的库是Zippy，它是一个围绕miniz库的对象化包装器。miniz库速度快，且仅包含头文件，非常适合OpenXLSX。

使用Zippy/miniz库无需特殊操作，开箱即用。

然而，如果你愿意，也可以选择使用不同的压缩库。在极少数情况下，你可能会遇到与miniz相关的稳定性问题，此时尝试使用其他压缩库可能是有益的。

在这里插入图片描述

🎄三、下载 OpenXLSX

OpenXLSX 可以在GitHub下载，地址是：https://github.com/troldal/OpenXLSX

在Tags里的不是最新版本，需要按照下图去下载其最新版本，下载后文件名为：OpenXLSX-master.zip

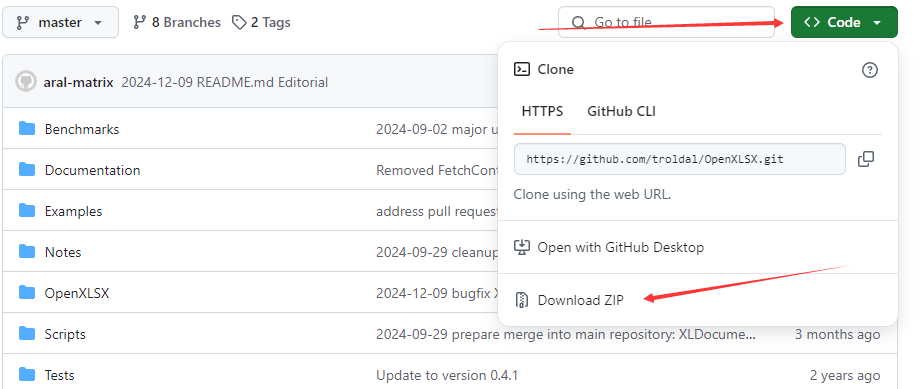
在这里插入图片描述

🎄四、编译 OpenXLSX

✨4.1 更新 cmake

OpenXLSX 采用 cmake 来编译，并且要求 cmake 的版本大于3.15，否则会报错，而 Ubuntu18.04 的 cmake 为3.10.2，所以会报如下错误：

CMake Error at CMakeLists.txt:4 (cmake_minimum_required):CMake 3.15 or higher is required.  You are running version 3.10.2
-- Configuring incomplete, errors occurred!

需要更新 cmake ，可以参考这篇文章：Ubuntu 18.04 更新 cmake 到最新版本 3.31.2

✨4.2 OpenXLSX在 Ubuntu18.04 编译

下面是完整的编译过程shell命令，

unzip OpenXLSX-master.zip
cd OpenXLSX-master
mkdir build_gcc
cd build_gcc
cmake ..  -DCMAKE_CXX_COMPILER=g++ \
-DCMAKE_INSTALL_PREFIX=`pwd`/../../result_gcc
make
make install

编译完成后，在 build_gcc 目录会有如下内容，其中 output/ 目录存放了一些使用例子：
在这里插入图片描述

✨4.3 OpenXLSX在 Ubuntu18.04 编译

下面是使用海思交叉工具链aarch64-mix210-linux-g++交叉编译的shell命令：

unzip OpenXLSX-master.zip
cd OpenXLSX-master
mkdir build_mix210
cd build_mix210
cmake ..  -DCMAKE_CXX_COMPILER=aarch64-mix210-linux-g++ \
-DCMAKE_INSTALL_PREFIX=`pwd`/../../result_mix210
make
make install

在这里插入图片描述

🎄五、使用 OpenXLSX

OpenXLSX 源码中有个 Examples 目录，里面有 8 个例子介绍了怎样使用 OpenXLSX 来操作 .xlsx 文件。感兴趣的可以看看，代码也不难理解。这里介绍一下怎样单独编译这些例子，虽然 cmake 时帮我们编译了，但是了解怎样去单独编译也是有益的。下面以编译 Demo1.cpp 为例，进入 Examples 目录，执行下面命令可以单独编译 Demo1.cpp。

g++ Demo1.cpp -I ../result_gcc/include/OpenXLSX/ -I ./ -std=c++17 ../result_gcc/lib/libOpenXLSX.a

我的项目只需要了解怎样写入就行了，下面是使用 OpenXLSX 写 .xlsx 文件的例子，仅供参考：

// myXlsxWrite.cpp
#include <OpenXLSX.hpp>
#include <iostream>using namespace std;
using namespace OpenXLSX;void writeRow(auto wks, int lineNum)
{// Axstring strA = "A" + std::to_string(lineNum);wks.cell(strA).value() = "Test";// Bxstring strB = "B" + std::to_string(lineNum);wks.cell(strB).value() = "";// Cxstring strC = "C" + std::to_string(lineNum);wks.cell(strC).value() = lineNum-2;// Dxstring strD = "D" + std::to_string(lineNum);wks.cell(strD).value() = lineNum%2==0 ? true : false;// Exstring strE = "E" + std::to_string(lineNum);wks.cell(strE).value() = 3.14159265358979323846;
}int main()
{XLDocument doc;doc.create("./xlsxWrite.xlsx");auto wks = doc.workbook().worksheet("Sheet1");wks.cell("A1").value() = "Col1";wks.cell("B1").value() = "Col2";wks.cell("C1").value() = "Col3";wks.cell("D1").value() = "Col4";wks.cell("E1").value() = "Col5";for(int i=0; i<1000; i++){writeRow(wks, i+2);}doc.save();doc.close();return 0;
}

编译：

g++ myXlsxWrite.cpp -I ./result_gcc/include/OpenXLSX/ ./result_gcc/lib/libOpenXLSX.a -std=c++17

注意：必须要支持 C++17 编译器才可以，且需要加-std=c++17。
运行后会生成xlsxWrite.xlsx，内容如下：
在这里插入图片描述

如果报如下错误，是缺少头文件：

In file included from ./result_gcc/include/OpenXLSX/headers/XLCellValue.hpp:64:0,from ./result_gcc/include/OpenXLSX/headers/XLCell.hpp:60,from ./result_gcc/include/OpenXLSX/OpenXLSX.hpp:49,from myXlsxWrite.cpp:1:
./result_gcc/include/OpenXLSX/headers/XLXmlParser.hpp:50:10: fatal error: external/pugixml/pugixml.hpp: 没有那个文件或目录#include <external/pugixml/pugixml.hpp> // not sure why the full include path is needed within the header file^~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
compilation terminated.

执行下面命令复制对应头文件：

cp OpenXLSX-master/Examples/external/ ./result_gcc/include/OpenXLSX/ -far

在这里插入图片描述

🎄六、总结

本文介绍 OpenXLSX开源库在 Ubuntu 18.04 的编译、交叉编译以及使用教程。

在这里插入图片描述
如果文章有帮助的话，点赞👍、收藏⭐，支持一波，谢谢 😁😁😁

参考：
https://blog.csdn.net/qq_37371407/article/details/141135709
https://gitcode.com/gh_mirrors/op/OpenXLSX/overview

目录

🎄一、概述

🎄二、OpenXLSX 介绍

🎄三、下载 OpenXLSX

🎄四、编译 OpenXLSX

✨4.1 更新 cmake

✨4.2 OpenXLSX在 Ubuntu18.04 编译

✨4.3 OpenXLSX在 Ubuntu18.04 编译

🎄五、使用 OpenXLSX

🎄六、总结

相关文章：