【力扣题目分享】二叉树专题(C++)

目录

1、根据二叉树创建字符串

代码实现：

2、二叉树的层序遍历

代码实现：

 变形题：

代码实现： 

3、二叉树的最近公共祖先

代码实现： 

 4、二叉搜索树与双向链表

代码实现： 

 5、从前序与中序遍历序列构造二叉树

代码实现：

 6、从中序与后序遍历序列构造二叉树

 代码实现：

7、二叉树的前序遍历(非递归)

代码实现：

 8、二叉树的中序遍历(非递归)

代码实现：

9、二叉树的后序遍历(非递归)

代码实现：

---

学了二叉树但不知道怎么用于做题？本篇将会讲解10道关于二叉树的力扣/牛客题，带大家二叉树进阶

1、根据二叉树创建字符串

 如果只看示例1，很有可能认为只要是空树就不加括号，但只要看了示例二，就知道如果右树存在的前提下，左树即使是空树，也不能省略括号

这道题可以用前序递归遍历来遍历节点，再通过判断当前节点的左右子树是否存在而决定是否加括号和继续递归

代码实现：

class Solution {
public:string tree2str(TreeNode* root) {string s;//先将根尾插进去s += to_string(root->val);//to_string函数可以把任何类型的数据转为stringif(root->left)//如果左子树存在，就继续递归(加括号){s += '(';s += tree2str(root->left);s += ')';}else if(root->right)//如果左子树不存在，但右子树存在，也加括号s += "()";if(root->right)//如果右子树存在，就继续递归(加括号){s += '(';s += tree2str(root->right);s += ')';}return s;}
};

2、二叉树的层序遍历

 先来讲讲普通的层序遍历

层序遍历也就是从上到下从左到右来遍历数据，这需要用到队列。将根节点入队后，出该数据时，再将该数据的左右子树入队

void levelOrder(TreeNode* root)
{if(root == nullptr)return;queue<TreeNode*> q;//用队列模拟层序q.push(root);while(!q.empty()){//提出队头数据并输出TreeNode* cur = q.front();q.pop();cout << cur->val << " ";//并将队头的左右子树入队if(cur->left)q.push(cur->left);if(cur->right)q.push(cur->right);}
}

但这还不符合题目要求，拿题目中的示例一来举例，现在代码输出的数据是

3 9 20 15 7 

看不出来哪个数据是第几层

而题目中要求要返回二维数组，每个二维数组中每个一维数组是一层数据

那么我们只需要知道每一层有几个数据，就可以通过控制循环的次数来分层插入

拿下面这棵树举例，第一层最多就只有1个节点。把根节点的数据入队后，此时队列的数据个数就是第一层的数据个数。提出队头数据并pop掉，将队头的数据的左右树也入队，此时队列的数据个数就是第二层的数据个数

 以此类推，到第二层的数据全出队并将左右子树入队后，队中数据个数就是第三层的数据个数

可以通过这个特性分层遍历

代码实现：

class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> vv;if(root == nullptr)return vv;queue<TreeNode*> q;//用来模拟层序遍历q.push(root);while(!q.empty()){vector<int> v;//每一层的数据int lengthnum = q.size();//lengthnum是每一层数据的总个数for(int i=0;i<lengthnum;i++)//当本层数据被出完后，队中的数据正好是下一层的数据个数{//取出队头数据，并将队头的左右子树入队TreeNode* cur = q.front();q.pop();v.push_back(cur->val);if(cur->left)q.push(cur->left);if(cur->right)q.push(cur->right);}vv.push_back(v);}return vv;}
};

 变形题：

该题和上一题唯一的区别就是要倒着层序遍历，这也很简单，可以用算法库（algorithm）中的reverse函数来逆置数组

代码实现： 

class Solution {
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {vector<vector<int>> vv;if(root == nullptr)//如果是空树，就直接返回空数组return vv;queue<TreeNode*> q;//用队列存树的节点q.push(root);while(!q.empty()){vector<int> v;int levelnum = q.size();//每次出完上一层的数据，队列中的数据个数正好是当前层的数据个数for(int i=0;i<levelnum;i++)//将当前层的数据出完{TreeNode* cur = q.front();//取出队头数据q.pop();v.push_back(cur->val);//将队头数据入到当前层数组//将左右孩子入队if(cur->left)q.push(cur->left);if(cur->right)q.push(cur->right);}vv.push_back(v);//将当前层数据(一维数组)尾差到二维数组中}reverse(vv.begin(),vv.end());//翻转数组return vv;}
};

3、二叉树的最近公共祖先

需要注意的是，节点本身也可以是自己的祖先，所以在示例二，5和4的祖先就是5本身

该题可以将输入划分为四种情况：

1. p和q都在左，就递归进入左子树继续判断
2. p和q都在右，就递归进入右子树继续判断
3. p和q一个在左一个在右，那当前根节点就是最深祖先
4. p和q有一个是当前根节点，那当前根节点就是最深祖先

终点其实就只有3,4两种情况，而1,2情况就会继续递归判断是3,4中的哪一种情况

那怎么知道p和q在左还是在右呢？
这里可以写一个Find函数，来递归遍历左右子树，找到p和q,判断出p和q分别在左树还是右树

bool Find(TreeNode* cur,TreeNode* goal)//递归遍历cur判断是否找到goal
{if(cur == nullptr)return false;if(cur == goal)return true;return Find(cur->left,goal) || Find(cur->right,goal);
}

下面以分别用示例一和示例二来模拟一下过程

示例一：

示例二：

代码实现： 

class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root == p || root == q)//如果p和q的其中一个就是root，那root就是最近公共祖先return root;//判断p和q在左还是在右bool pInLeft,pInRight,qInLeft,qInRight;pInLeft = Find(root->left,p);pInRight = !pInLeft;qInLeft = Find(root->left,q);qInRight = !qInLeft;if(pInLeft && qInLeft)//如果p和q都在左，就往左树递归return lowestCommonAncestor(root->left,p,q);else if(pInRight && qInRight)//如果p和q都在右，就往右树递归return lowestCommonAncestor(root->right,p,q);return root;//如果能走到这一步，就说明p和q一个在左，一个在右}//每次判断都只会有：p和q都在左、p和q都在右、一个在左一个在右、pq中有一个是根节点，这四种情况，而如果是前两种，就继续递归判断bool Find(TreeNode* cur,TreeNode* goal)//递归遍历cur判断是否找到goal{if(cur == nullptr)return false;if(cur == goal)return true;return Find(cur->left,goal) || Find(cur->right,goal);}
};

 4、二叉搜索树与双向链表

 简单点来讲，就是将节点的left视作链表的prev，right视作链表的next，用升序的排列将二叉树链接起来。

众所周知，二叉搜索树的中序遍历(InOrder)就是升序遍历，所以本题就可以用中序遍历的节奏来链接节点

示例一链接完的关系是这样

 但是在递归途中，访问不到节点的父亲，也不知道哪个孩子是它的前一个

所以这道题需要用到双指针思想：定义一个prev和cur指针，cur指向当前节点，而prev指向上一个节点(上次递归的cur)，这样就可以让cur和prev完成双向链接，那cur和next的链接怎么办？在下次递归中，prev就变成了当前的cur，cur就变成了下一个节点，这样每次递归都可以链接当前节点和上一个节点。

下面来模拟一下示例一的过程

代码实现： 

class Solution {
public:TreeNode* Convert(TreeNode* pRootOfTree) {TreeNode *cur = pRootOfTree,*prev = nullptr;InOrderList(cur, prev);//因为二叉搜索树的中序遍历就是有序，所以用中序遍历递归的顺序去链接//链接完后，找到该链表的头，并返回while(cur && cur->left){cur = cur->left;}	return cur;}void InOrderList(TreeNode* cur,TreeNode*& prev)//prev必须传引用，这样才能保证当前栈帧中改变的prev能应用到其他栈帧中{if(cur == nullptr)//如果是空，就跳出return;InOrderList(cur->left,prev);//先遍历左子树//此时左子树的根节点就通过34行赋给prev了，如果prev不是引用，下面的操作就不对了cur->left = prev;//将当前节点的左指向上一个节点if(prev)prev->right = cur;//将上一个节点的右指向当前节点//此时就将当前节点和上一个节点的链接完成了，因为找不到下一个节点，所以当前节点和下一个节点的链接只能在下次递归时完成prev = cur;//将当前节点变成上一个节点，这样在下面递归时才能将上当前节点和下一个节点链接InOrderList(cur->right,prev);}
};

 5、从前序与中序遍历序列构造二叉树

 在前序遍历中，节点遍历顺序是根、左、右子树，因此数组的第一个元素就是根。中序遍历的节点遍历顺序是左、根、右子树，那只要先通过前序遍历找到根节点，再通过中序遍历找到根节点所在的位置，判断它有没有左右子树。如果有左子树，那前序遍历的第二个元素就是左子树的根，如果没有左子树，那前序遍历的第二个元素就是右子树的根，再将第二个元素进入递归，如此往复。

但如果直接把整个中序数组传过去也不行，拿示例一中的20来举例

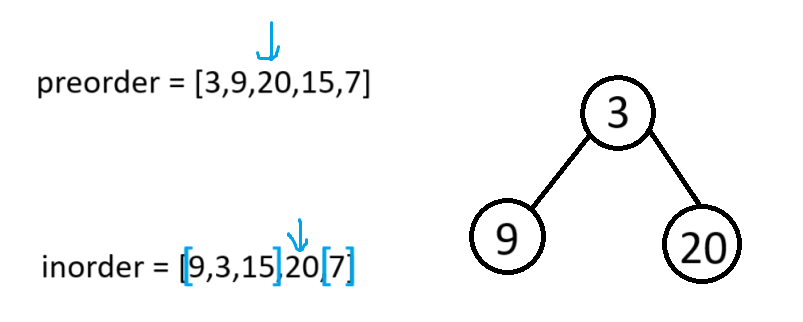
如果这里直接传整个中序数组过去， 那20的左子树就会被认成[9,3,5]所以我们要传一个只包含当前树节点的中序区间

下面来模拟一下示例一的过程

每次递归都要先在inorder中找到preorder[prei]的位置，以判断左右子树有没有数据

第一次递归，把preorder[0]当作根节点，[0,inorder.size()-1]当作当前根节点的中序区间，进去

据inorder的区间可知，当前根节点有左子树，所以prei+1的位置就是左子树的根节点(若没有左子树，那prei+1的位置就是右子树的根节点，那root->left就会置空)所以root->left会以preorder[++prei](也就是9)为根节点，[0,0]为下一个根节点的中序区间，进递归

此时，因为根节点的左右两边就没有数据，因此没有节点给此时的root->left和root->right，就都置空后返回上一个栈帧。

此时根的左子树的递归结束，又因为根的右子树也有节点(若右子树没节点，前序数组就遍历完了，再将root->right置空)，所以root->right会以preorder[++prei](也就是20)为根节点，[2,4]为下一个根节点的中序区间，进入递归

此时因为根节点的左子树有数据(若左子树没数据，prei+1的位置就是右子树的根，左子树就置空了)，所以root->left就会以preorder[++prei](也就是15)为根节点，[2,2]为下一个根节点的中序区间，进递归

此时因为根节点的左右子树都没有数据，所以root->left和root->right都置空并返回上一个栈帧

此时根节点的左树递归结束，又因为右树也有数据(若右子树没数据，前序遍历就结束了，二叉树的构建也结束了，把root->right置空)，所以root->right就会以preorder[++prei](也就是7)为根节点，[4,4]为下一个根节点的中序区间，进递归

此时，因为7的左右子树都没节点，所以将root->left和root->right置空，并返回上一个栈帧

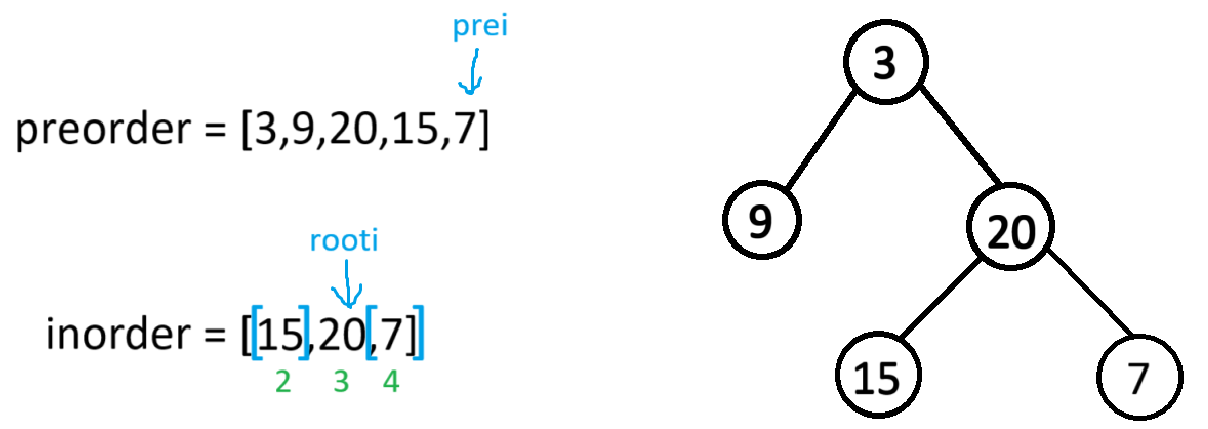
此时root的左右子树也都访问完了，就返回上一个栈帧

此时root的左右子树也都访问完了，就返回到主函数中了

栈帧模拟图：

代码实现：

class Solution {
public:TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int prei=0,inbegin=0,inend=inorder.size()-1;return _buildTree(preorder,inorder,prei,inbegin,inend);//用递归去构建}TreeNode* _buildTree(vector<int>& preorder,vector<int>& inorder,int& prei,int inbegin,int inend)//prei必须是引用，才能保证prei每次递归进入都会+1{TreeNode* root = new TreeNode(preorder[prei]);//为当前节点开辟空间//找到根节点在中序区间的位置int rooti = inbegin;while(rooti <= inend){if(preorder[prei] == inorder[rooti])break;rooti++;}//此时中序区间就变成了[inbegin,rooti-1] rooti [rooti+1,inend],左边是rooti的左子树，右边是rooti的右子树if(inbegin <= rooti-1)//如果左子树有节点root->left = _buildTree(preorder,inorder,++prei,inbegin,rooti-1);//将左子树的根节点和中序遍历传过去递归elseroot->left = nullptr;if(rooti+1<=inend)root->right = _buildTree(preorder,inorder,++prei,rooti+1,inend);elseroot->right = nullptr;return root;}
};

 6、从中序与后序遍历序列构造二叉树

本题也可以用和上一题一样的思路

在前序遍历中，找根节点很容易，第一个节点就是根节点；在后序遍历中，找根节点同样很容易，最后一个节点就是根节点。

先通过后序数组找到根节点，再通过中序数组找到根节点所在位置，判断左右子树有无节点，如果有节点，去递归它的左右子树

不过本题后序数组传参时就不能传根节点的下标了，刚开始下标-1确实是右子树的根，但再-1就是右子树的右子树的根，但我们想要的是左子树的根。因此本题后序数组也需要传子树的后序区间

在后序遍历中，右子树的根也就是当前下标-1，那左子树的根怎么找呢？

 可以先通过中序区间，知道当前根节点的左树有多少个节点

int leftnum = rooti - inbegin;//中序区间中当前根节点所在下标减去中序区间的开始下标

此时后序区间就可以被分为

[postbegin,postbegin+leftnum-1][postbegin+leftnum,postend-1] postend
//[后序区间的开始下标,后序区间开始下标+左子树节点个数-1][后序区间开始下标+左子树节点个数,后序区间结束下标-1] 后序区间结束下标

再分别递归左子树和右子树

下面模拟一下示例一的过程

 每次进入递归都会计算出中序区间左树的节点个数，这样可以算出后序区间的左右子树区间

此时根节点的左子树有数据，所以root->left就会以[0,0]为后序区间，[0,0]为中序区间进入递归

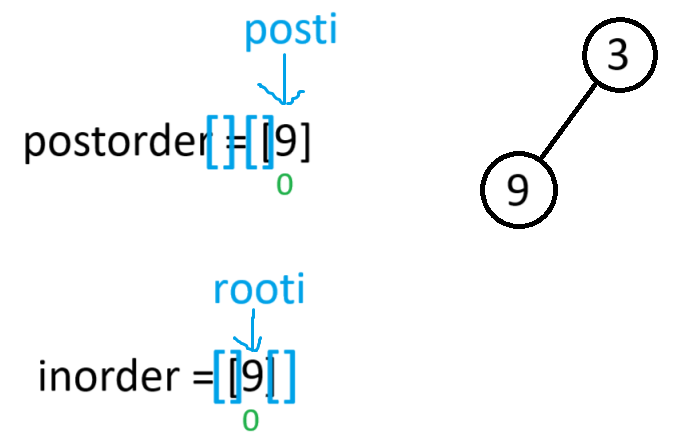
此时根据中序区间可判断出根节点没有左右子树，因此将root->left 和 root->right置空 并返回上一栈帧

此时当前根节点的左子树构建完毕，又因为右子树也有节点，所以root->right就会以[1,3]为后序区间，[2,4]为中序区间，进递归

此时根据当前根节点的中序区间可知，左子树有节点，因此root->left就会以[1,1]当作后序区间，[2,2]当作中序区间，进递归

此时根据当前根节点的中序区间可以判断出左右都为空，那么就将root->left和root->right置空后返回上一栈帧

此时当前根节点的左子树构建完，又因为右子树中也有数据，所以root->right就会以[2,2]当作后序区间，[4,4]当作中序区间，进递归

 此时根据当前根节点的中序遍历可以判断出左右子树为空，所以将root->left和root->right置空后返回上一栈帧

此时当前根节点(20)的左右子树均构建完毕，返回上一栈帧

此时当前根节点(3)的左右子树均构建完毕，返回主函数

栈帧模拟图： 

 代码实现：

class Solution {
public:TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {int postbegin = 0,postend = postorder.size()-1;//当前根节点的后序区间int inbegin = 0,inend = inorder.size()-1;//当前根节点的中序区间return _buildTree(inorder,postorder,inbegin,inend,postbegin,postend);//通过递归构建}TreeNode* _buildTree(vector<int>& inorder,vector<int>& postorder,int inbegin,int inend,int postbegin,int postend){TreeNode* root = new TreeNode(postorder[postend]);//为当前根节点开辟空间//从中序区间中找到根节点的位置int rooti = inbegin;while(rooti <= inend){if(inorder[rooti] == postorder[postend])break;rooti++;}//此时中序区间就变成了[inbegin,rooti-1] rooti [rooti+1,inend]//判断当前根节点是否有左右树int leftnum = rooti - inbegin;//计算出左树节点的个数，就可以知道右树的节点个数//此时后序就被分成了[postbegin,postbegin+leftnum-1][postbegin+leftnum,postend-1] postend//先递归右子树，因为后序遍历的顺序是左、右、根，右子树在紧跟在根节点的前面if(inbegin <= rooti-1)//如果右子树有节点root->left = _buildTree(inorder,postorder,inbegin,rooti-1,postbegin,postbegin+leftnum-1);elseroot->left = nullptr;//再递归左子树if(rooti+1 <= inend)//如果左子树有节点root->right = _buildTree(inorder,postorder,rooti+1,inend,postbegin+leftnum,postend-1);elseroot->right = nullptr;return root;}
};

7、二叉树的前序遍历(非递归)

 若要用递归来解这道题，非常简单

class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {vector<int> v;preorder(v,root);return v;}void preorder(vector<int>& v,TreeNode* root){if(root == nullptr)//判断该节点是否存在return;v.push_back(root->val);//根preorder(v,root->left);//左子树preorder(v,root->right);//右子树}
};

本篇的思路重点讲解非递归

前序遍历的特点是先访问根，再访问左子树，最后访问右子树

可以把遍历分为两步：

1. 遍历左路节点
2. 左路节点的右子树

先遍历当前根节点的左路节点，这样就完成了前序的根、左子树操作

 

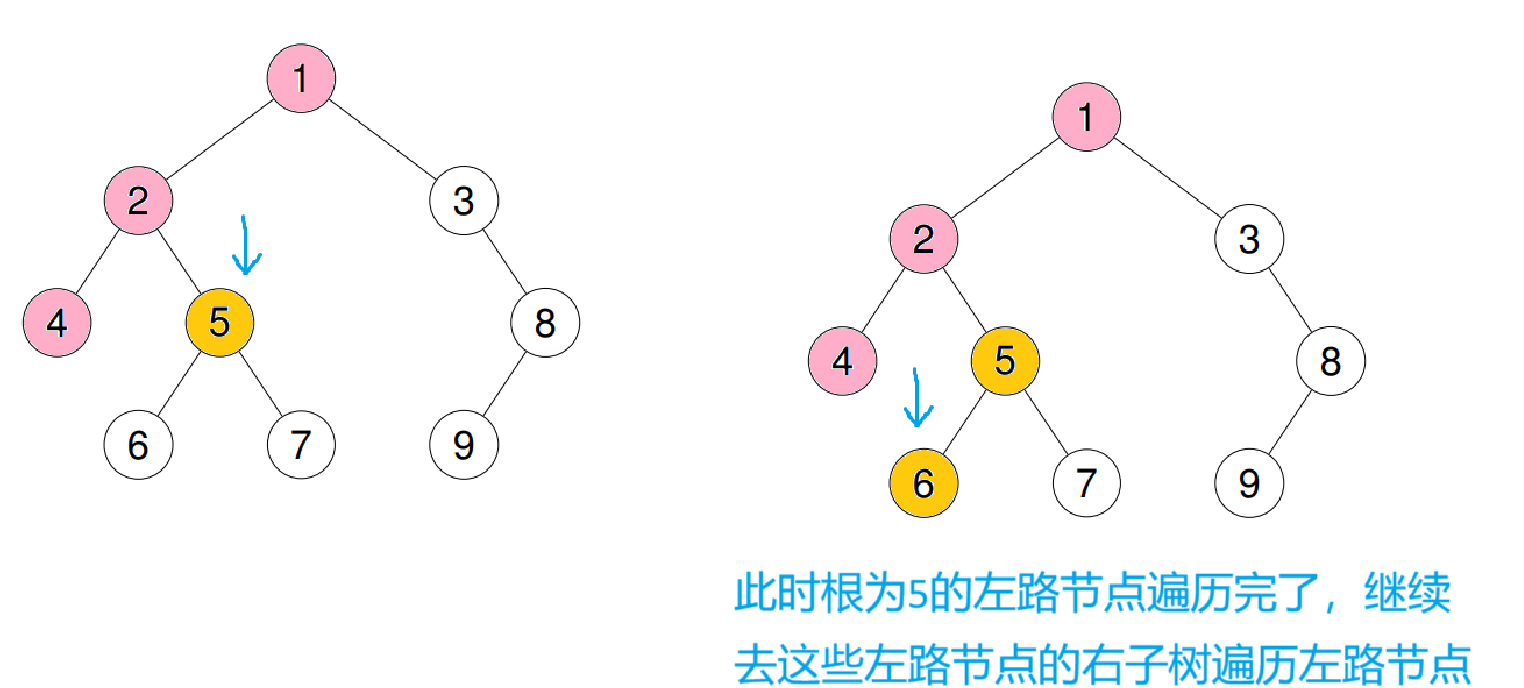
 这样就用前序的顺序完成了遍历 

那怎么才能知道这些左路节点有没有被访问过呢？

可以用栈模拟栈帧，每次遍历一个左路节点时，就把它本身入栈，它就算一个子树，直到左路节点遍历完(left == nullptr)时，再去提取栈顶的右子树继续遍历左路节点，如此往复

拿示例二来举例，下面模拟一下过程

这是第一次进循环，直到cur为空时跳出

cur = st.top()->right后继续进循环(别忘了st.pop()删除栈顶数据)

 4的右子树也为空，此时跳出循环，继续把栈顶数据右树给cur(cur = st.top->right)，进循环

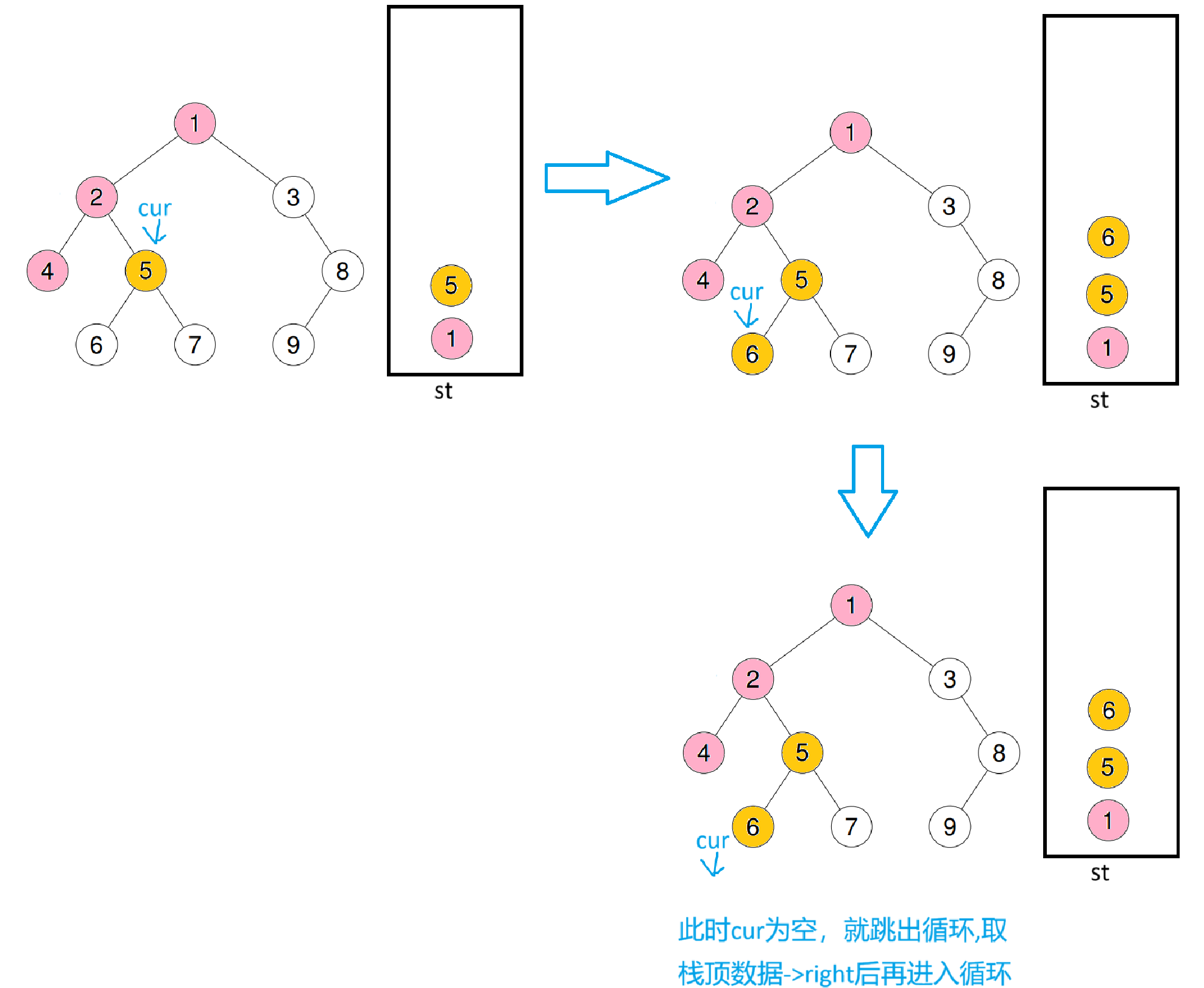
 跳出循环后肯定就证明cur为空，所以直接cur = st.top()->right ;st.pop();后再进入循环

重复之前操作后再入循环

 此时cur又会跳出循环，重复之前操作后再进循环

由于7的右子树是空，也不会进循环，继续重复之前操作

将3压入栈后，又会跳出循环，此时继续重复之前操作后再进入循环

 此时cur为空跳出，继续cur = st.top()->right;st.pop();后入循环

代码实现：

class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {vector<int> v;if(root == nullptr)return v;stack<TreeNode*> st;//用栈模拟递归栈帧TreeNode* cur = root;while(cur || !st.empty())//第一次进循环时栈为空，所以要加上另外一个条件{while(cur)//1.遍历左路节点访问根并入栈{v.push_back(cur->val);st.push(cur);cur = cur->left;}cur = st.top()->right;//2.取栈顶节点的右子树，继续遍历左路节点访问并入栈st.pop();}return v;}
};

 8、二叉树的中序遍历(非递归)

本题也可以采用前序遍历非递归的思路，只不过这次遍历左路节点时不能直接把值尾插到数组中，因为中序遍历是顺序是左子树、根、右子树，要在取栈顶数据时把值尾插到数组中

下面还是用刚才的二叉树来模拟一下过程 

此时cur为空，就跳出循环。但这里就不能直接将cur = st.top()->right了，直接略过节点，就不能把值尾插到数组中了，所以这里要改为

v.push_back(st.top()->val);
cur = st.top()->right;
st.pop();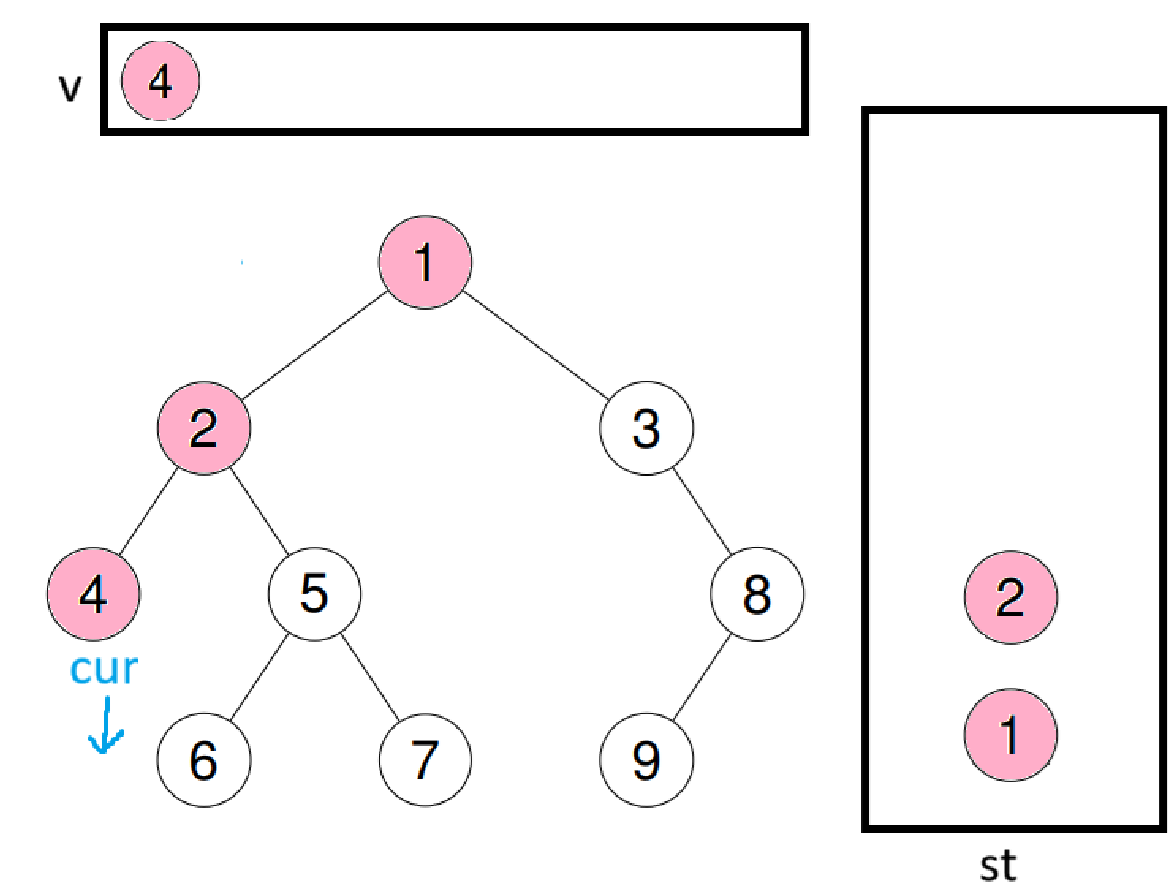

先将栈顶值尾插到数组中，再将栈顶的右子树给cur

此时因为4的子树还是空，所以再跳出循环，将栈顶值尾插到数组中后，再将栈顶右子树给cur

此时再取出栈顶数据尾插到数组中，再将栈顶数据的右子树赋给cur，进入循环

 左树剩余过程

 右树剩余过程

代码实现：

class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> v;if(root == nullptr)//如果是空树，就返回空数组return v;stack<TreeNode*> st;//用栈模拟递归栈帧TreeNode* cur = root;while(cur || !st.empty())//因为第一次进循环时栈为空，所以多加一个条件{while(cur)//遍历左路节点，但不尾插到数组中{st.push(cur);cur = cur->left;}//取栈顶的右子树之前先将栈顶值尾插到数组中v.push_back(st.top()->val);cur = st.top()->right;st.pop();}return v;}
};

9、二叉树的后序遍历(非递归)

 后序的非递归也可以用前序和中序的思路

后序遍历的顺序是左、右、根，按照上面的思路：先将左路节点入栈，直到cur->left == nullptr，此时要先遍历右树，再将根尾插进数组

如果遍历完的是左子树，就要再去右树继续入栈；如果遍历完的是右子树，此时就要出栈顶数据并尾插到数组中

要想能够判断刚遍历完的是左树还是右树，就需要除了cur指针外，再有一个指针用来指向上一个尾插进数组的节点，也就是双指针。因为后序遍历的顺序是左、右、根，所以对于一棵树的子树而言，最后一个被尾插进数组的肯定是根节点

例如，此时取出栈顶是2，只需要判断2的右子树是否为lastnode或空。

若不是，就代表右树还未遍历，就先去遍历cur->right；

若是右子树，就代表右树已经遍历完，就需要让栈顶出栈并尾插到数组中

此时lastnode变成了2，cur现在变成了1，根据上面步骤可得此时要先走1的右子树，以此类推

 下面以示例二来模拟一下过程

此时因为刚刚尾插了4节点，lastnode会指向4，cur再指向栈顶数据(即2)

此时lastnode会指向6，会取出栈顶数据(也就是5)，判断栈顶->right是不是lastnode或空，因为不是，所以会将cur = st.top()->right继续入循环

此时lastnode会指向7，再取出栈顶数据5，判断栈顶->right是否等于lastnode或空，因为是，代表右子树访问完毕，就出栈并尾插进数组

此时lastnode会指向5，再取出栈顶数据2，判断栈顶->right是否为lastnode或空，因为是，所以出栈并尾插进数组

此时lastnode会指向2，取出栈顶数据1，判断栈顶->right是否为lastnode或空，因为不是，所以将cur = st.top()->right继续进循环

此时last会指向9，取出栈顶数据8，因为8的右子树也是空，所以出栈并尾插进数组

此时lastnode会指向8，取出栈顶数据3，因为3的右节点就是lastnode，代表右子树已访问完毕，所以出栈并尾插进数组

此时lastnode会指向3，再取出栈顶数据1，此时因为1的右节点就是lastnode，代表右子树访问完毕，所以出栈并尾插进数组

此时因为栈为空，代表遍历完毕。

代码实现：

class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> v;stack<TreeNode*> st;//用栈模拟递归栈帧TreeNode* cur = root;TreeNode* lastnode = nullptr;//定义一个指向上一个尾插节点的指针while(cur || !st.empty()){while(cur)//入栈左路节点{st.push(cur);cur = cur->left;}if(st.top()->right == lastnode || st.top()->right == nullptr)//如果栈顶的右节点等于lastnode或空，就代表右子树访问完毕，可以将当前根节点尾插进数组{    v.push_back(st.top()->val);lastnode = st.top();//更新lastnodest.pop();}else//如果右子树还没被遍历，就先遍历右子树的左路节点{cur = st.top()->right;}}return v;}};