Bellman - Ford 算法与 SPFA 算法求解最短路径问题 ——从零开始的图论讲解(4)

目录

前言

为什么Dijkstra算法面对负权值图会有误差???

举例说明

什么是Bellman -Ford算法?

BF算法的核心思想 

什么是松弛 

为什么最多松弛N-1次?

代码实现

举例

 初始状态（dist[] 数组）

 第 1 轮松弛（遍历所有边）

第 2 轮松弛

第 3 轮松弛

第 4 轮松弛（最后一次）

第 5 轮检测是否还能松弛（负环判断）

完整代码

 BF算法的缺陷

SPFA算法

SPFA算法改进的地方

SPFA算法的原理

完整代码

结尾

---

前言

这是笔者图论系列的第四篇博客了,非常感谢大家的支持,因为本系列的数据很好看,笔者有了更多动力去更新 .

前三篇URL如下:

1.

图的概念,图的存储,图的遍历与图的拓扑排序——从零开始的图论讲解(1)_图论】图的存储与出边的排序-CSDN博客

2.

Dijkstra算法求解最短路径—— 从零开始的图论讲解(2) -CSDN博客

3.

Floyd算法求解最短路径问题——从零开始的图论讲解(3)-CSDN博客

其中第二篇与第三篇笔者已经介绍了两种算法去解决最短路径问题了

 Dijkstra 是一种"单源" 最短路径算法,它的利用了贪心的思维,效率相当高,唯一的遗憾是当权值为负时,可能会产生误差

为什么Dijkstra算法面对负权值图会有误差???

因为它的核心是:

每次从未访问的点中，选择一个 当前距离起点最近的点 u，然后从 u 出发去更新其他点的距离（“松弛”操作）。

也就是说，它一旦确定了一个点 u 到起点的最短路径，就永远不会再改变它 —— 因为它“相信”这个距离已经是最短的。

举例说明

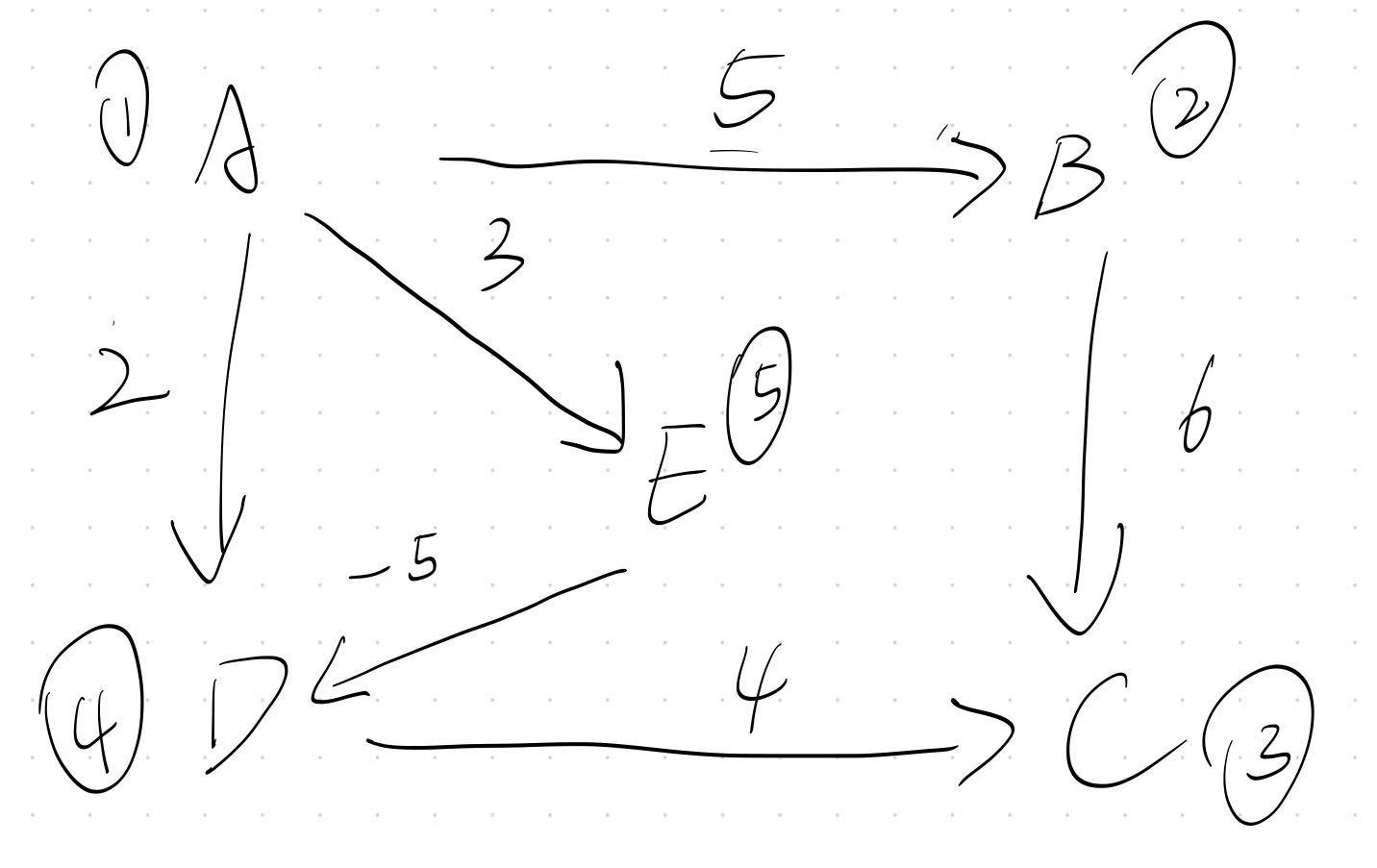
举例来说,请看下面的图:

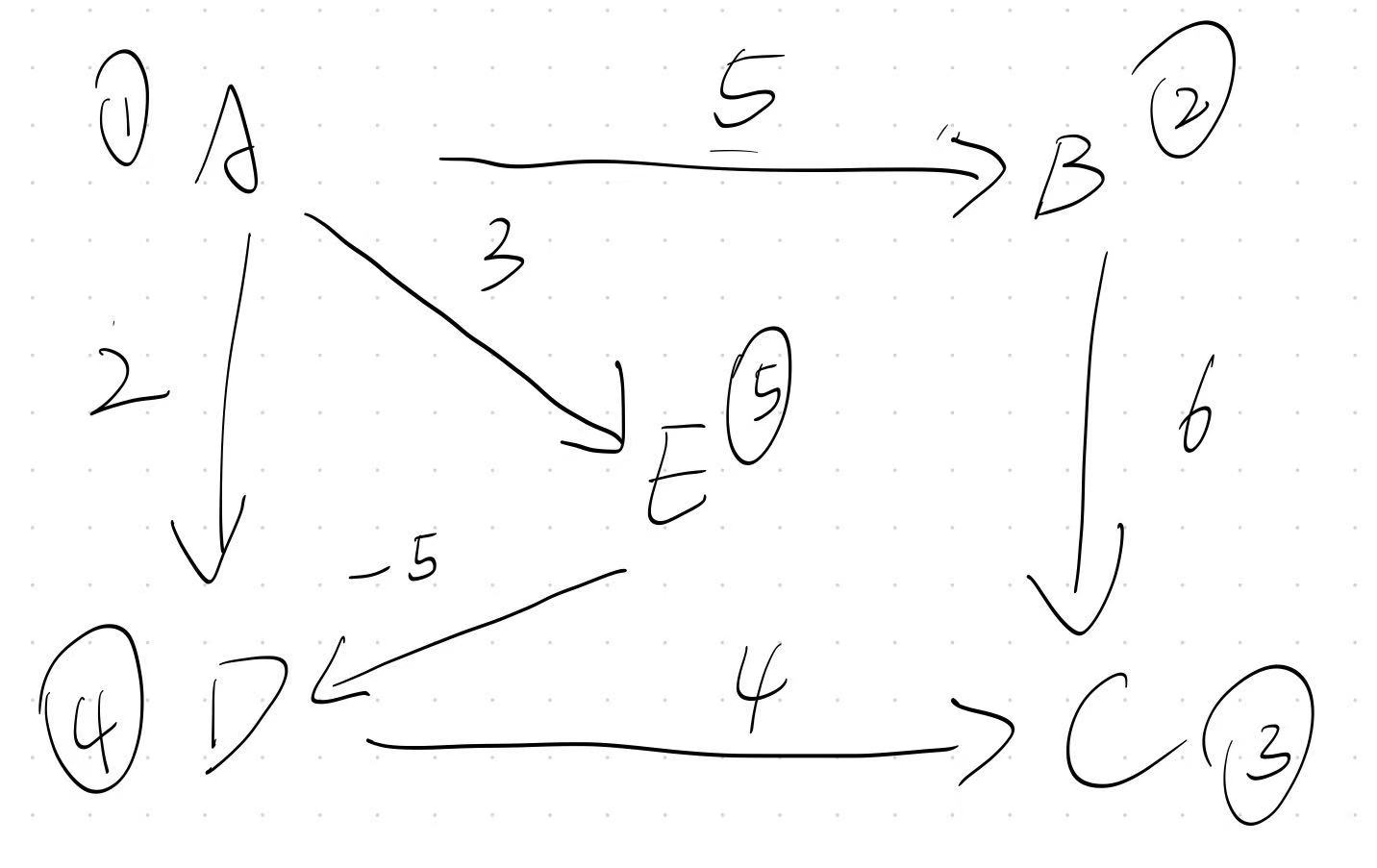
  如果以A(1)点为源点,且使用Dijkstra 算法,那么效果如下:

 显然,问题出在点 A 到 点 C的距离上,从图上我们就很好的看出来了

   如果走 A - E - D - C, A到E的距离将会是2,但是答案中的数字却是6

   这是因为,Dijkstra 算法帮我们规划的路径是 A - D - C

为什么Dijkstra 算法会带领我们走一条错误的路, 看似更近了,实则更远了呢?

我们简单过一下 Dijkstra 算法的流程

第一轮:

第一轮中距离 A 点最近的点是 D 点 我们通过 D 点 更新 A 点 到 C 点的距离 

此时 dis[3] == 6, vis[4] == true, 也就是说, 在 Dijkstra 算法, A 到 D点的距离已经被定死了,

---

这个定死指的不是 A 到 D的距离不会变了,事实上你看图也知道是会变的

而是说,在算法的视角里,我们已经得出了 源点 A , 通过走节点D, 达到别的节点的最短距离了

比如上面的点C, 哪怕后面D的距离确确实实变小了 ,  Dijkstra 算法 也不会给你二次更新的机会

所以哪怕到了后面,我们知道了借节点E到达节点D的距离是-2,是更小的,此时再到点C的距离就变成2了,但是 Dijkstra 算法是不知道的,因为它的标准是 先找距离源点最近的点去更新距离

点E一开始明明离我更远,D是更近的,我怎么后续又可以通过点E去缩短到达D的距离呢? 

\0/这不是扯鬼淡吗\0/

所以资料上才会说, Dijkstra 算法没有考虑过负权边的场景 

Dijkstra 的算法缺陷和实例举例,我已经在第二篇介绍Floyd 时具体的介绍过了,上述的例子复习一下.

而Floyd 算法 确实可以解决好上述问题,也就是说,即使存在负权值,也可以求出最短路径,而且是任意点到任意点之间的最短距离.

但是Floyd 算法也有缺陷,它利用动态规划的思维保存了所有点到点直接的距离,也因此,它的算法复杂度是O(n^3). 适用于数据量不大的密集图,但是不适用于数据量大且稀疏的图了

正因如此,我们可以学习一下BF算法和他的优化版本 SPFA 算法,  它们和Dijkstra 算法一样,是"单源路径"算法. 但是它们可以解决带负权值图的 最短路径问题.

其中SPFA 算法是对于BF算法的优化 , 但为了让读者们更好入门,笔者先介绍 BF算法,然后再介绍SPFA算法

什么是Bellman -Ford算法?

Bellman-Ford 算法是一个用于求解单源最短路径问题的经典算法，支持图中存在负权边的情况。它的核心优点在于：

• 相比 Dijkstra 算法，允许边的权值为负；

• 能够判断图中是否存在 负权环（负环）；

• 时间复杂度为 O(N * M)，其中 N 是节点数，M 是边数。

Bellman-Ford 算法适用于以下几种情况：

• 图中存在负权边；

• 需要判断是否存在负权环；

• 点数不大，允许一定的时间复杂度。

BF算法的核心思想 

Bellman-Ford 算法的核心思想可以用一句话概括：

“对每条边进行最多 N-1 轮松弛操作，如果第 N 轮仍可松弛，则说明图中存在负环。”

(请注意 N-1 的松弛次数,这个次数不是随便来的,为什么后面会说)

什么是松弛 

 在图论中，松弛（Relaxation） 是一种操作，用来尝试更新某个点的最短路径估计。

通俗一点来说：

假设现在我们知道从起点到某个点 v 的最短距离是 dist[v]，
如果我们找到了一条从 u 到 v 的边（权重为 w），
且 dist[u] + w < dist[v]，
那我们就有理由相信“走 u → v 比原来的方案更短”，
那么我们就 更新 dist[v] = dist[u] + w —— 这就是一次“松弛”。

为什么最多松弛N-1次?

 那么,为什么说"对每条边进行最多 N-1 轮松弛操作"呢?

我们先思考一个问题：在一个没有环的图中，从节点 1 到节点 N，最多可能经过多少条边？

答案是 N−1 条边。为什么？想象图的结构是一个链表，即 1 → 2 → 3 → ... → N，这种情况下从起点到终点正好需要经过 N−1 条边。

从节点1到节点N,就是把所有节点穿起来的过程,自然是经过N-1条边的

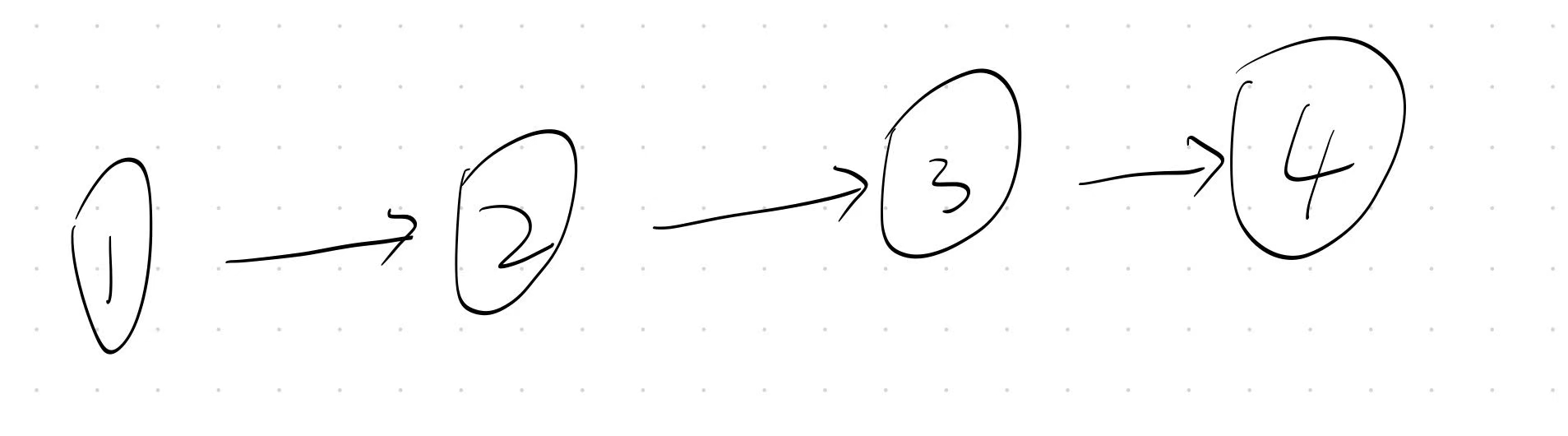
(从节点1到4,需要经过三条边)

但是这个 最多松弛N-1次  有什么关系? 

既然任意一条最短路径最多只包含 N−1 条边，那么我们只需要“尝试”最多 N−1 次从起点出发、借助其他节点“中转”，就能将所有最短路径更新到位。如果我可以通过节点A 的道路缩短达到 源点S 的距离,那我何乐而不为呢? 

这就是 Bellman-Ford 算法最多执行 N−1 轮松弛操作的原因：每一轮我们都会遍历所有边，尝试进行松弛（即检查是否存在更短的路径），通过反复借道尝试，在 N−1 轮内，所有最短路径一定能够被更新正确。

代码实现

下面是一个标准的 Bellman-Ford 算法 Java 实现。笔者一步一步解释代码中的关键点，帮助读者理解每一处设计背后的原因.

1.图的存储结构：边列表

static class Node {int u, v, w;public Node(int u, int v, int w) {this.u = u;this.v = v;this.w = w;}
}
static List<Node> edges = new ArrayList<>();

Bellman-Ford 算法是“按边松弛”的最短路径算法，因此我们使用**边的列表（edge list）**而非邻接表或邻接矩阵。每条边用一个 Node 对象表示，其中：

•  u 表示边的起点，

•  v 表示边的终点，

•  w 表示这条边的权重。

2. 初始化最短路径数组

static final int INF = Integer.MAX_VALUE / 2;
dist = new int[n + 1];
Arrays.fill(dist, INF);
dist[start] = 0;

• 定义 dist[i] 表示从起点出发到节点 i 的当前最短距离。

• 一开始将所有节点距离初始化为无穷大，表示“不可达”。

• 起点到自己的距离是 0。

使用 INF == Integer.MAX-VALUE/2  是为了避免后续加法操作时发生溢出。

3.核心逻辑：边的松弛操作

for (int i = 1; i <= n - 1; i++) {for (Node edge : edges) {int u = edge.u, v = edge.v, w = edge.w;if (dist[u] < INF) {dist[v] = Math.min(dist[v], dist[u] + w);}}
}

• 外层循环进行 N-1 轮松弛操作（N 是点的个数）。

• 每一轮遍历所有边，尝试“借道”某个点更新路径。

• 只要 dist[u] + w < dist[v]，说明经过 u 再走这条边能得到更短的路径，就更新 dist[v]。

举例

我们在开头用了一份带有负权边的图,来体现Dijkstra的缺陷,现在我们依然用它来体现为什么

BF算法可以用来处理带负权值的图

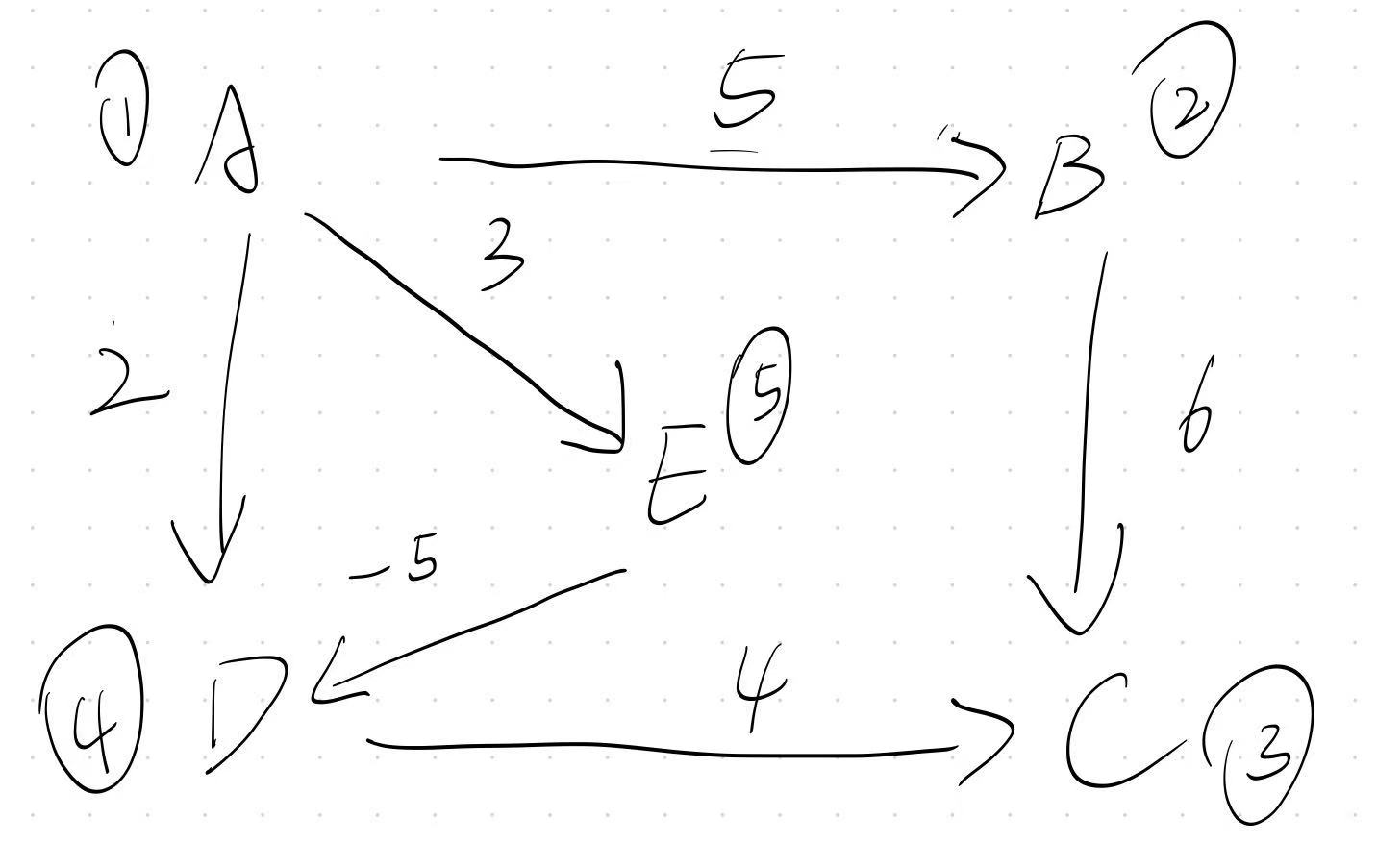
我们接下来模拟一遍算法

 图中共有 5 个点、6 条边，编号为 1 到 5，边的定义如下：

1 → 2 权重 5
1 → 4 权重 2
1 → 5 权重 3
2 → 3 权重 6
4 → 3 权重 4
5 → 4 权重 -5

 初始状态（dist[] 数组）

dist[1] = 0      // 起点自己到自己为 0
dist[2] = ∞
dist[3] = ∞
dist[4] = ∞
dist[5] = ∞

没有什么特别需要主义的问题

 第 1 轮松弛（遍历所有边）

边逐个松弛如下：

1. 1 → 2，5 → dist[2] = min(∞, 0+5) = 5

2. 1 → 4，2 → dist[4] = min(∞, 0+2) = 2

3. 1 → 5，3 → dist[5] = min(∞, 0+3) = 3

4. 2 → 3，dist[2] 已更新为 5 → dist[3] = min(∞, 5+6) = 11

5. 4 → 3，dist[4] = 2 → dist[3] = min(11, 2+4) = 6

6. 5 → 4，dist[5] = 3 → dist[4] = min(2, 3+(-5)) = -2  发生了逆转,这个在Dijkstra算法也有体现

更新后 dist 数组为：

dist[1] = 0
dist[2] = 5
dist[3] = 6
dist[4] = -2
dist[5] = 3

第 2 轮松弛

再次遍历所有边：

1. 1 → 2 无更新

2. 1 → 4 无更新

3. 1 → 5 无更新

4. 2 → 3 → dist[3] = min(6, 5+6) = 6 （无变化）

5. 4 → 3，dist[4] = -2 → dist[3] = min(6, -2+4) = 2  更新成功

6. 5 → 4，dist[5] = 3 → dist[4] = min(-2, 3+(-5)) = -2（无变化）

请大家尤其注意标红的第五步,这是 BF算法能正确得出结果而Dijkstra算法无法得到正确结果的原因

具体来说, Dijkstra算法压根不会有第五步,因为 此时的 节点4(D) 已经被标记为True了

但是我们的BF算法可不管你那么多,它是一种非常暴力的做法,每一轮都要扫一遍,这样你在上一轮松弛中的任何改变都会被继承下来,进而影响下一轮松弛

dist[1] = 0
dist[2] = 5
dist[3] = 2
dist[4] = -2
dist[5] = 3

第 3 轮松弛

再次遍历所有边：

1. 1 → 2 无变化

2. 1 → 4 无变化

3. 1 → 5 无变化

4. 2 → 3 → min(2, 5+6) = 2（不更新）

5. 4 → 3 → min(2, -2+4) = 2（不更新）

6. 5 → 4 → min(-2, 3+(-5)) = -2（不更新）

第 4 轮松弛（最后一次）

全部边遍历后依然无任何更新，说明最短路径已经收敛

dist[1] = 0
dist[2] = 5
dist[3] = 2
dist[4] = -2
dist[5] = 3

第 5 轮检测是否还能松弛（负环判断）

进行一次额外的遍历，发现所有边都无法再更新，说明图中不存在负权环，算法正确结束。

(关于负环问题,后面会单独开博客讲的)

最后的效果如图所示

 

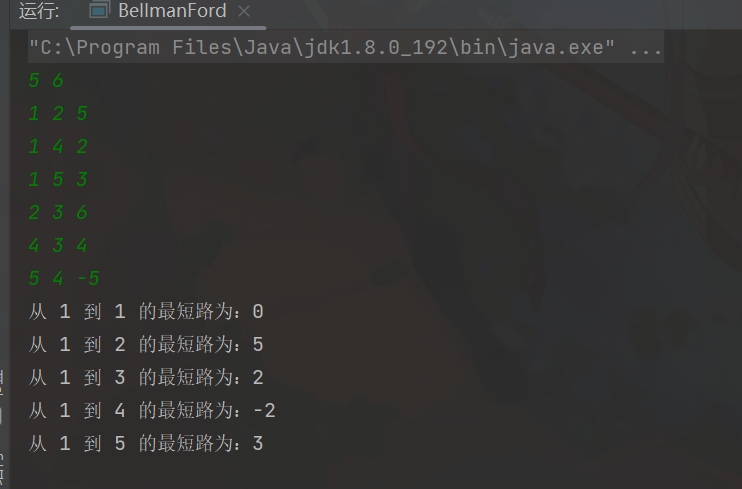
完整代码

import java.util.*;public class BellmanFord {static class Node {int u, v, w;public Node(int u, int v, int w) {this.u = u;this.v = v;this.w = w;}}static final int INF = Integer.MAX_VALUE / 2;static int n, m;static int[] dist;static List<Node> edges = new ArrayList<>();
//Bellman-Ford 是一个“按边遍历”的最短路算法，所以直接维护一个边的列表是最简单、最直接的做法，不需要邻接表！public static boolean bellmanFord(int start) {dist = new int[n + 1];Arrays.fill(dist, INF);dist[start] = 0;// 最多进行 n - 1 次松弛for (int i = 1; i <= n - 1; i++) {for (Node edge : edges) {int u = edge.u, v = edge.v, w = edge.w;if (dist[u] < INF) {dist[v] = Math.min(dist[v], dist[u] + w);}}}// 第 n 次遍历判断是否仍能松弛，判断是否有负环for (Node edge : edges) {int u = edge.u, v = edge.v, w = edge.w;if (dist[u] < INF && dist[u] + w < dist[v]) {return false; // 存在负环}}return true; // 无负环}public static void main(String[] args) {Scanner sc = new Scanner(System.in);n = sc.nextInt();m = sc.nextInt();for (int i = 0; i < m; i++) {int u = sc.nextInt(), v = sc.nextInt(), w = sc.nextInt();edges.add(new Node(u, v, w));}boolean ok = bellmanFord(1);if (!ok) {System.out.println("存在负权环");} else {for (int i = 1; i <= n; i++) {if (dist[i] >= INF / 2) {System.out.println("到达 " + i + " 不可达");} else {System.out.println("从 1 到 " + i + " 的最短路为：" + dist[i]);}}}}
}

 BF算法的缺陷

 虽然笔者提到过了,BF算法可以解决Dijkstra算法的缺陷——即负权边图问题,但这并不代表BF算法没问题,事实上,它的问题也很明显,时间复杂度太高太高了

Bellman-Ford算法的时间复杂度为 O(V×E)，其中 V 是图中的顶点数，E 是边数。在稠密图中，这个复杂度可能会非常大，导致算法运行效率很低，尤其是在顶点和边的数量都很庞大的情况下，实际应用中会变得不够实用。相比之下，Dijkstra算法在使用优先队列优化后可以达到 O(Elog⁡V) 的复杂度，明显更高效。

此外，Bellman-Ford算法需要进行最多 V−1 轮的松弛操作，每一轮都遍历所有边。这种“暴力”遍历的方式虽然保证了算法的正确性，但也造成了大量重复计算，浪费了计算资源。

那么有没有改进措施的,当然是有的家人们,这就是SPFA算法

SPFA算法

SPFA的算法和BF别无二致,都是通过不停地松弛边来求得最短距离,但是他改进了如下地方

SPFA算法改进的地方

1. 减少无效松弛，避免遍历所有边

   • Bellman-Ford 每次循环都遍历所有边进行松弛操作，重复且浪费，尤其是很多边已经不需要松弛了。

   • SPFA 只对“可能改进最短路径”的顶点对应的边进行松弛，通过维护一个队列，动态入队出队顶点，避免盲目遍历所有边。

2. 动态维护更新顶点集合

   • SPFA维护一个队列，只有当某个顶点的距离被更新时，才将该顶点加入队列，等待松弛它的邻边。

   • 这样只处理“活跃”的顶点，大幅减少冗余计算。

3. 利用队列结构实现“宽度优先式”的松弛

   • SPFA的队列结构让顶点按松弛顺序逐层推进，类似于BFS的遍历方式，这种方式更快找到最短路径的更新方向。

4. 入队次数检测负环

   • 通过统计每个顶点入队次数，如果超过顶点数（V），说明存在负权回路，能够及时停止并报

基于以上改进,SPFA的算法原理就是:

SPFA算法的原理

• 初始时，将源点入队，距离初始化为0，其它点为无穷大。

• 每次从队列头取出一个顶点 u，遍历它的所有邻边 (u,v)

  • 如果能通过 u 松弛 v（即 dist[u]+w(u,v)<dist[v]），就更新 dist[v]

  • 并且如果 v 不在队列中，则将 v 入队。

• 重复上述过程直到队列为空，表示没有可以进一步松弛的边了。

• 若某顶点入队次数超过 V 次，判定存在负权回路。

总结一下就是,SPFA相比BF算法,每次松弛不会访问所有的点,只会访问"距离被访问过"的点,例如上述例子的4(D) 点

完整代码

import java.util.*;public class SPFA {static class Edge {int to, weight;public Edge(int to, int weight) {this.to = to;this.weight = weight;}}static int N, M, S;static List<List<Edge>> graph;static int[] dist;static boolean[] inQueue;static final int INF = Integer.MAX_VALUE / 2;public static void spfa(int start) {Queue<Integer> queue = new LinkedList<>();dist[start] = 0;queue.offer(start);inQueue[start] = true;while (!queue.isEmpty()) {int u = queue.poll();inQueue[u] = false; // 标记出队for (Edge edge : graph.get(u)) {int v = edge.to, w = edge.weight;if (dist[v] > dist[u] + w) {dist[v] = dist[u] + w;if (!inQueue[v]) { // 避免重复入队queue.offer(v);inQueue[v] = true;}}}}}public static void main(String[] args) {Scanner in = new Scanner(System.in);N = in.nextInt();M = in.nextInt();
//        S = in.nextInt();graph = new ArrayList<>(N + 1);dist = new int[N + 1];inQueue = new boolean[N + 1];Arrays.fill(dist, INF);for (int i = 0; i <= N; i++) {graph.add(new ArrayList<>());}for (int i = 0; i < M; i++) {int u = in.nextInt();int v = in.nextInt();int w = in.nextInt();graph.get(u).add(new Edge(v, w));}spfa(1);for (int i = 1; i <= N; i++) {System.out.print((dist[i] == INF ? -1 : dist[i]) + " ");}}
}

 最后效果如下:

结尾

本篇博客到此结束,博客主要介绍了BF算法和SPFA在解决单元最短路径方面的作用,但是,它们同样可以判断负环,具体是怎么样的,笔者打算再开一篇博客梳理一下.感谢大家阅读到此