当前位置：首页 > news >正文

考研408《计算机组成原理》复习笔记，第二章(2)数值数据的表示和运算（浮点数篇）

news 来源：原创 2025/6/24 22:10:44

一、回顾定点数知识点

——定点小数机器码表示

——定点整数机器码表示

——【原码】和【移码】的作用

二、浮点数表示

1、概念引入

我们生活中有很多 “带小数”，也就是浮点数，也就是【整数部分】和【纯小数部分】都不为0，那么这样的小数是不可以按之前【定点数】的形式表达的，如下图：

定点数的小数点是固定死的，这样就不够灵活，无法应对对整数或小数要求高精度的表达方式

我们有时会有对整数或小数单独要求高精度的需求

所以我们希望小数点是可以浮动的，并不是固定在最左或最右，而小数点的位置和正负号这些规则都能按照一个规则来计算出来

那么我们希望用专门的浮点数表示规则来表示【浮点数】

于是参考十进制表示浮点数的形式，小数点可以浮动，【一个带小数 * 10的不同幂次】可以表示一个浮点数（即数学里的 “科学计数法”！！）

我们会发现：当小数点往左移动一位(整数变小)，为了保证原数值不变，就要乘一个2；小数点往右移(整数变小)，为了保证数值不变，就要除一个2；

简而言之：2的次幂对于小数点的移动是【左加右减】(不用自己算，知道就行，例子如下)

2、二进制浮点数的“科学计算法”公式

那么我们得出了【二进制表示浮点数】的公式：

我留意到网上大部分公式都是这样，这其实是简化的公式，没有考虑正负号的（了解有这么回事就行，不然会像我一开始发现负数对不上这个公式而懵逼。。。）

（忽略正负符号的形式）

;

实际上，准确的公式应该是

（不忽略正负符号的准确形式）

解释：

N：浮点数真值
S：是整个浮点数的符号，正数S=0、负数S=1
M：尾数，即0.11 * 2^2、1.1 * 2^1、11 * 2^0......红色部分(非正式数，仅作例子)
通常是一个定点整数，用原码表示
但是不管是普通浮点数还是后面学的IEEE754浮点数，整数部分都会被规定死是一个约定好的数(普通浮点数，整数那就是0；IEEE754浮点数，整数那就是1)，所以也没必要存它，大家都心知肚明这是什么数（具体规则后面会解释）
结论：所以【M(尾数)】实际只由【小数部分】代表

R^E：阶数，即0.11 * 2^2、1.1 * 2^1、11 * 2^0......黄色部分(非正式数，仅作例子)
其中R是基数，二进制通常都是2，所以大家都知道R=2就没必要存它了(有时也会约定为2、4、16，但正常情况都是2)
E是阶码或指数，这是不定的，所以要存储（通常是一个定点小数，用移码表示）
结论：所以【阶数】实际上也只由【E阶码(或指数)】代表

（暂时忽略符号）

；

总结：

1、N= (-1)^S × M × R^E ————> 真值 = (-1)正负号 × 尾数 × 阶数
2、实际尾数只用【尾数的小数部分】表示
3、实际阶数只用【阶数的指数部分】表示

3、浮点数机器码规则

1）浮点数机器码的组成

那么实际的机器码是如何表示刚刚的公式的？

1、三部分：【整个浮点数的符号位】+【阶码】+【尾码】
2、其中【阶码】包含了【阶符 (阶数的正负号)】和【阶数 (切记只是指数部分)】
3、其中【尾码】就是【尾数 (切记，只是是小数部分)】

（这里可能会有人不理解，为什么在尾数后面补0？之前【零扩展】和【符号扩展】不都是在前面补0吗？因为tmd这尾数是【小数部分】啊，小数部分后面补0和原来的值有什么区别？？？）

2）求阶码的公式

但是这里需要重点注意【阶码】部分，【阶码】不只单纯是原来阶数的值

我们前面学过【移码】，【浮点数的阶码】就是用【移码】表示

（因为其他码会让机器在比较大小时误认为负数大于正数，而移码可以明确比较正数值大于负数值，不理解的看我之前的文章：考研408《计算机组成原理》复习笔记，第三章数值数据的表示和运算（定点数篇）-CSDN博客，也不是重要知识点）

；

；

那么牢记这两个公式：

并且注意，全部按照 “无符号数形式” 去计算

；

例子1：

阶码是7位，则阶码的真值7-1=6位，应该是【偏置值 = 2^6 =64】

3）浮点数和真值之间转换

根据这个公式就可以推导浮点数转换

【浮点数真值——>浮点数机器码】

假设条件：

32位的浮点数，其中阶码7位，尾数24位

真值是：-0.011001000000000000000000

【浮点数机器码——>浮点数真值】

假设条件：

32位的浮点数，其中阶码7位，尾数24位

机器码是：1 10101111 011001000000000000000000

4）浮点数机器码可表示范围

如何理解上面的范围，看下面例子解释：

以 “32位的浮点数，其中阶码7位，尾数24位” 为例子

;

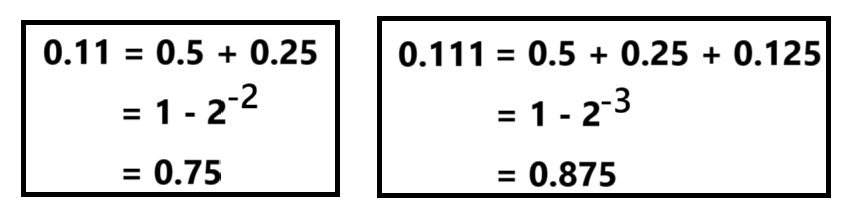
首先前提知识点：我们知道N位的定点整数数部分连续全是1的话，其值就是【2^N-1】;而N位的定点小数如果后面连续全是1的话，其值就是【1-2^-N】，比如0.111就是1-2^-3=0.875

;

1、先看【正数】情况

最大值

（当然【阶码真值】你也可以按【移码最大值2^(N-1)-1】求得）

最小值

（当然【阶码真值】你也可以按【移码最小值-2^(N-1)】求得）

溢出

正数部分超出最大值叫正上溢、超出最小值的范围是正下溢，正下溢部分一般直接当作0处理；正上溢部分后面讲规格化的时候才会涉及，暂时不说

；

2、再看负数，知道正数范围就可以推负数范围了

最大值

最小值

溢出

负数部分超出最小值叫负上溢、超出最大值的范围是负下溢，负下溢部分一般直接当作0处理（正下溢和负下溢都称 “下溢”）；正上溢部分后面讲规格化的时候才会涉及，暂时不说（正上溢和负上溢都叫 “上溢”）

4、普通浮点数规格化

1）为什么规格化

那么我们前面我们在研究浮点数真值和机器码转换的时候反复提到，知道【尾码】就默认知道【尾数】是【0.尾码】，整数部分固定是0，究竟有什么道理？

首先十进制的最正确的科学计数法应该是【整数部分只有1位】，二进制也是

然后尾数的位数决定了浮点数的有效数位，假设只能保留有限的几位小数的话，那么肯定是非零的小数部分保留的越多，精度越高。所以为了让有效数位占满尾数数位，我们必须进行规格化。

2）怎么规格化

规格化就是通过调整【阶码】和【尾码】，使得一个非零的浮点数在【尾数的最高位上】是一个有效数值！

具体措施：【左规】和【右规】

左规就是整数和小数点不动，小数部分往左移（其实就是小数点往后移位）

右规就是整数和小数点不动，小数部分往右移（其实就是小数点往前移位）

规格化后的机器码尾码是啥样的？

补充：不同基数r，会导致不同的规格化

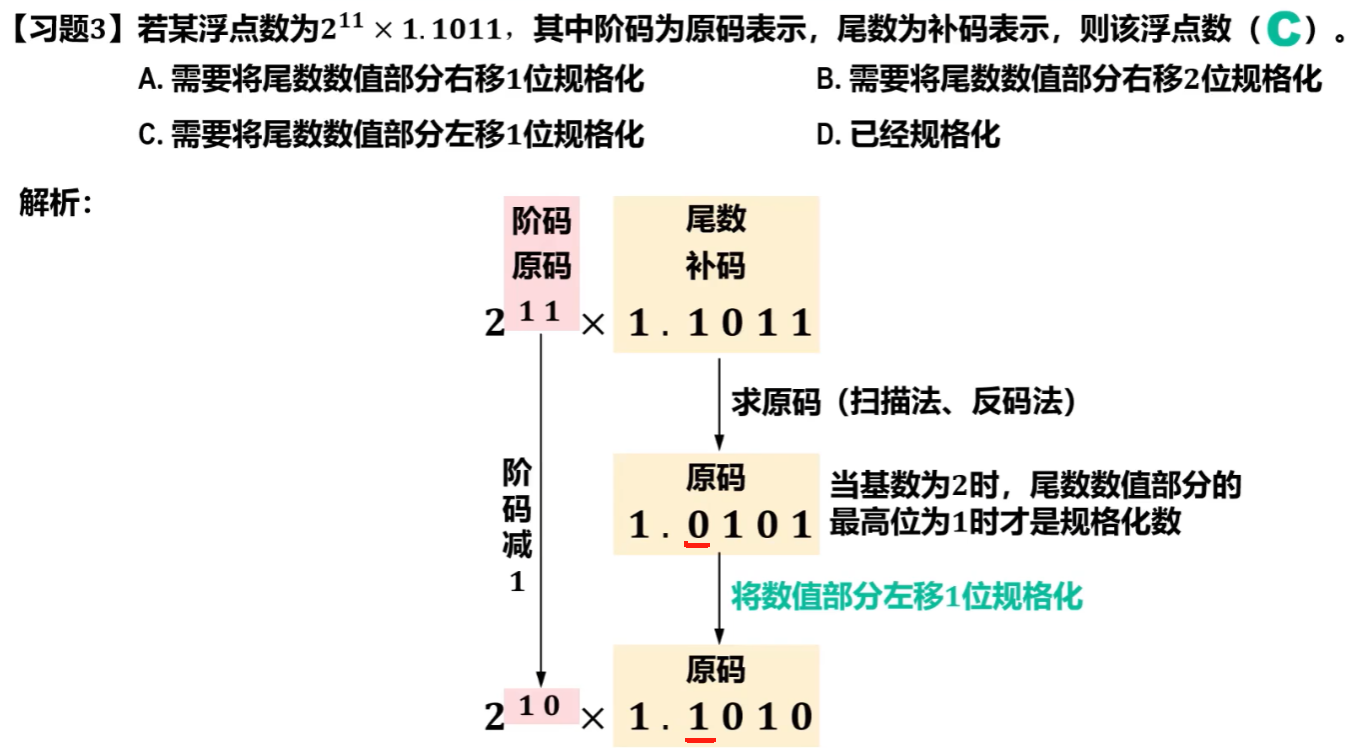
3）例题

5、IEEE 754规范

1）表示规则

但是那帮研究计算机的逼养的还是不爽啊，就非还要在整一些新的规则出来，好嘛没办法，最后IEEE754这套浮点数规范就是一直沿用至今的一套规范。

他要求就两种浮点数表示法：

1、单精度浮点数Float
4字节 (32位)，其中1符号位、8阶码位、23位尾码（记牢了！！！！）
【偏置值】：2^(8-1)-1 = 127位（区分一下，普通浮点数是2^(N-1) ）

2、双精度浮点数Double
8字节 (64位)，其中1符号位、11阶码位、52位尾码（记牢了！！！！）
【偏置值】：2^(11-1)-1 = 1023位（区分一下，普通浮点数是2^(N-1) ）

留意和【普通浮点数】的区别：

1、同样位数的阶码条件下，【IEEE754】的【偏置值】比【普通浮点数】的【偏置值】偏置值多1，而且IEEE754的移码的【全1】和【全0】有别的用途，阶码不能用这两（下图是32位的单精度的阶码例子）

2、普通浮点数在规格化后也只是尾数最高位是1，而IEEE754浮点数要求是整数部分是1！！！

（没什么办法去理解，很无奈我本人也看遍了全网所有视，没有一个解释清楚的，只能死记硬背。。。。。。）

2）IEEE754浮点数机器码和真值的转换

【浮点数机器码——>浮点数真值】

【浮点数真值——>浮点数机器码】

3）IEEE754浮点数机器码可表示范围

解释：

只以单精度为例子，注意这里【阶码】我就不按普通浮点数那么细致地用偏置值算了，直接用【移码】可表示地最大最小值来推导即可

；

【规格化情况】：整数部分是1，值 = 1 + 小数部分

【正数情况】

1、最小值（阶码是： - (移码最小值绝对值-2) ）

；

2、最大值（阶码是：移码最大值）、

；

【负数情况】

没什么好说的，【负数最小值】就是【 - 正数最大值】，【负数最大值】就是【- 正数最小值】，加个负号的事

；

；

；

；

【非规格化情况】：

1、整数部分为0，值 = 0 + 小数部分
2、阶码全0，尾码不全为0
3、偏置值是126（别问为啥那么，我tm也不知道，全网没人讲为什么，只能死记硬背）

【正数情况】

1、最大值

2、最小值

【负数情况】

没什么好说的，【负数最小值】就是【 - 正数最大值】，【负数最大值】就是【- 正数最小值】，加个负号的事

；

4）解惑：为什么IEEE754的阶码是移码，但不能和补码转换再求真值？

因为我们要记住：

1、普通浮点数的偏置值是正常的，偏置值是【2^(N-1)】时，阶码可以按照【移码<——>补码】原则（移码和补码就是符号位取反，其他位一样）
2、IEEE754浮点数的偏置值是不正常的！！他的偏置值是【2^N-1】，所以不可以用【移码<——>补码】

5）IEEE754规格化

没什么好说的，就区别于普通浮点数：要把整数部分规格化成一个1，最终变成【1.M】形式就行

6）需要死记硬背的知识点

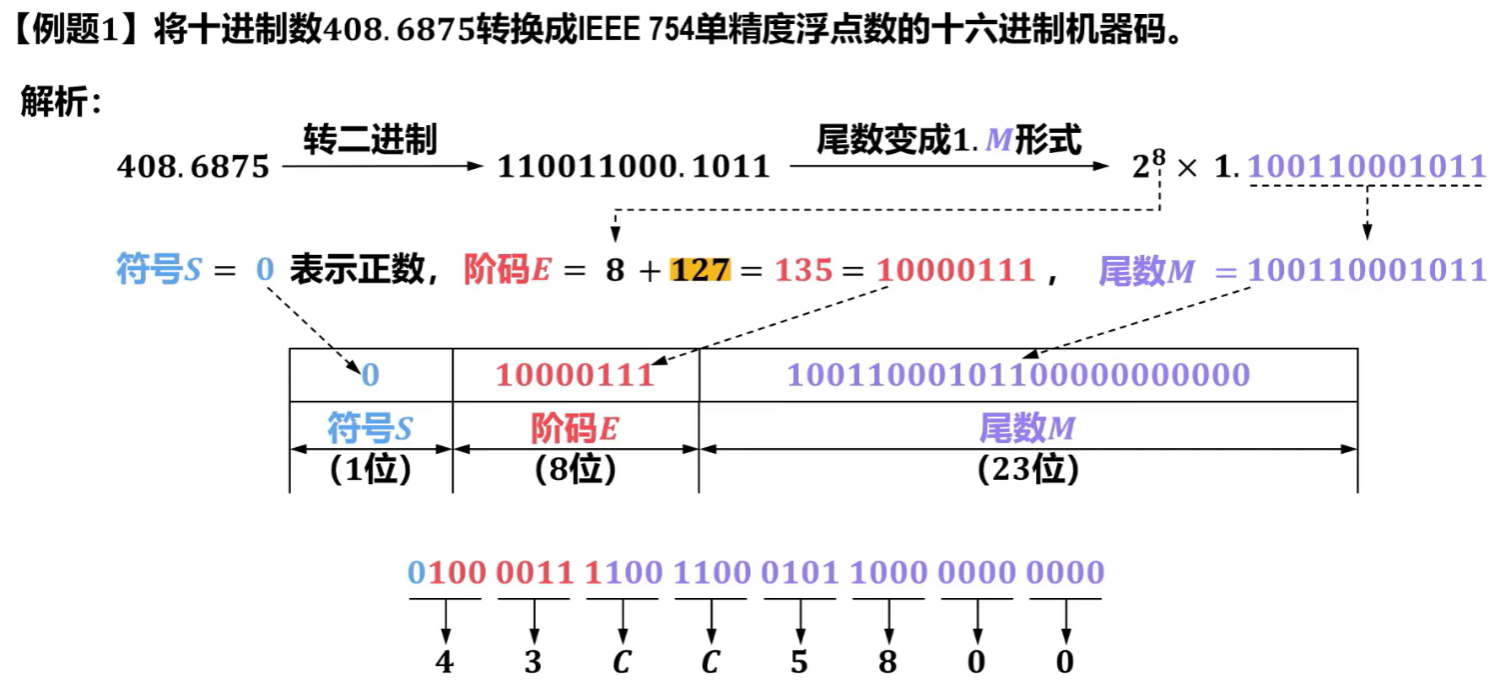
7）转换类型例题

小技巧：可以留意float的浮点数机器码后面0~20(后5个字节)基本都是为了补0的没用数，然后这些数可以直接不看了，浪费时间

8）范围类型例题

浮点数运算我在下一篇文章讲

考研408《计算机组成原理》复习笔记，第二章(2)数值数据的表示和运算（浮点数篇）

一、回顾定点数知识点 ——定点小数机器码表示 ——定点整数机器码表示 ——【原码】和【移码】的作用二、浮点数表示 1、概念引入我们生活中有很多 “带小数”，也就是浮点数，也就是【整数部分】和【纯小数部分】都不为0，那么这样的小数…...

编程日记 2025/6/24 22:10:44

【虚幻引擎】UE5独立游戏开发全流程（商业级架构）

本套课程我将会讲解一下知识 1.虚幻引擎的常用功能节点、模块包含但不限于动画模块、UI模块、AI模块、碰撞模块、伤害模块、背包模块、准心模块、武器模块、可拾取物品模块、死亡等模块。 2.整个游戏的设计思路（游戏架构），本套教程讲解了如…...

编程日记 2025/6/25 5:49:05

大语言模型 08 - 从0开始训练GPT 0.25B参数量 - MiniMind 单机多卡 torchrun deepspeed

写在前面 GPT（Generative Pre-trained Transformer）是目前最广泛应用的大语言模型架构之一，其强大的自然语言理解与生成能力背后，是一个庞大而精细的训练流程。本文将从宏观到微观，系统讲解GPT的训练过程，…...

编程日记 2025/6/25 13:50:23

使用gitbook 工具编写接口文档或博客

步骤一：在项目目录中初始化一个 GitBook 项目 mkdir mybook && cd mybook git init npm init -y步骤二：添加书籍结构（如 book.json, README.md） echo "# 我的书" > README.md echo "{}" > bo…...

编程日记 2025/6/19 23:26:13

Mysql视图详解

文章目录 1、视图简介 && 前置准备2、基本crud语法3、检查选项（with check option）CASCADEDLOCAL总结 4、视图更新限定条件 1、视图简介 && 前置准备视图 (View) 是一种虚拟存在的表。视图中的数据并不在数据库中实际存在，…...

编程日记 2025/6/25 13:47:44

题目描述代码： class Solution {struct Interval{int left;int right;Interval(int l0,int r0):left(l),right(r){}bool operator<(const Interval& rhs) const{return left<rhs.left;}};public:vector<vector<int>> merge(vector<vecto…...

编程日记 2025/6/19 23:55:59

Mac 环境下 JDK 版本切换全指南

概要在 macOS 上安装了多个 JDK 后，可以通过系统自带的 /usr/libexec/java_home 工具来查询并切换不同版本的 Java。只需在终端中执行 /usr/libexec/java_home -V 列出所有已安装的 JDK，然后将你想使用的版本路径赋值给环境变量 JAVA_HOME，…...

编程日记 2025/6/25 13:40:32

【生活相关-日语-日本-东京-搬家后-引越（ひっこし）（3）-踩坑点：国民健康保险】

【生活相关-日语-日本-东京-搬家后-引越（ひっこし）（3）-注意点：国民健康保险】 1、前言2、情况说明（1）问题说明（2）情况说明（1）收到情况&#xff08…...

编程日记 2025/6/25 13:51:30

C++ asio网络编程(6)利用C11模拟伪闭包实现连接的安全回收

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档文章目录前言一、智能指针管理Session二、用智能指针来实现Server的函数1.start_accept()1.引用计数注意点2.std::bind 与异步回调函数的执行顺序分析 2.handle_accept1.异步…...

编程日记 2025/6/22 14:12:49

【视频】解决FFmpeg将RTSP转RTMP流时，出现的卡死、出错等问题

1、简述如果不修改图像内容，可以使用FFmpeg命令来将RTSP转RTMP流。 SRS视频服务器就是这么干的，它没有使用FFmpeg接口，而是直接使用FFmpeg命令来转流。但是在使用中，约到了一些问题，比如转流时卡死、转流出错等等，下面描述怎么解决这些问题 2、出错重启在shell脚本…...

编程日记 2025/6/23 22:38:03

飞牛NAS本地部署开源TTS文本转语音工具EasyVoice与远程使用流程

文章目录前言1. 环境准备2. Docker部署与运行3. 简单使用测试4. 安装内网穿透4.1 开启ssh连接安装cpolar4.2 创建公网地址 5. 配置固定公网地址总结前言本文主要介绍如何在fnOS飞牛云NAS使用Docker本地部署一款非常好用的开源TTS文本转语音工具EasyVoice，并结合…...

编程日记 2025/6/22 1:09:21

STC51系列单片机引脚分类与功能速查表（以STC89C52为例）

1. 基本I/O端口端口引脚范围类型主要功能特殊说明P0P0.0~P0.7开漏双向I/O1. 通用I/O（需外接上拉电阻） 2. 数据总线（D0-D7） 3. 低8位地址总线（A0-A…...

编程日记 2025/6/20 5:01:03

recvfrom和sendto函数中地址参数的作用

在 UDP 通信中，recvfrom 和 sendto 函数中的地址参数起着至关重要的作用。以下是对这两个函数中地址参数的作用、所属方以及缺失地址时的后果的详细解释。 recvfrom 函数 int recvfrom(int sockfd, void *buf, size_t len, int flags, struct sockaddr *src_add…...

编程日记 2025/6/22 14:56:54

运维职业发展思维导图

主要内容如下：一、初级入行阶段这是职业生涯的起点，主要涉及基础技能的学习和实践。 Linux初学：重点是学习Linux系统的基础命令和操作。IDC机房运维：负责数据中心机房内设备的管理和日常维护工作。Helpdesk桌面运维：提供桌面技术支持，帮助用户解决遇到的计算机软硬…...

编程日记 2025/6/23 21:23:22

【数据处理】Python对CMIP6数据进行插值——详细解析实现（附源码）

目录 Python对CMIP6数据进行插值一、引言代码概览思维导图二、数据预处理三、数据区域裁剪四、插值（一） 垂直插值（二） 水平插值五、保存插值好的文件六、文件合并与气候态计算七、代码优化技巧八、多线程处理九、全部代码 Pytho…...

编程日记 2025/6/1 15:48:20

worldquant rank函数

https://support.worldquantbrain.com/hc/en-us/community/posts/13869304934935-%E6%80%8E%E6%A0%B7%E7%90%86%E8%A7%A3rank%E5%87%BD%E6%95%B0 链接。进的话可以填我的邀请码JS34795我可以带你现在学习rank函数我们所说的做多和做空首先，当我们讨论Long和S…...

编程日记 2025/6/22 2:06:26

工业4.0神经嫁接术：ethernet ip转profinet协议通信步骤图解

在现代工业自动化领域，不同品牌的设备和协议之间的兼容性问题一直是个挑战。我们的包装线项目就遇到了这样的难题：需要将Rockwell Allen-Bradley的EtherNet/IP伺服系统与西门子PLC的PROFINET主站进行无缝对接。为了解决这一问题，我们采用了et…...

编程日记 2025/6/21 18:30:36

数据库——数据操作语言DML

（2）数据操作语言DML 简称DML——Data Manipulation Language用来对数据库中表的记录进行更新关键字：insert,delete,update A、插入表记录向表中插入数据格式：insert into 表名(字段1,字段2,字段3……) values(值1,值2,值3);…...

编程日记 2025/6/22 17:30:35

文件防泄密的措施有哪些?

文件防泄密措施需要从技术、管理和物理三个层面综合施策，以下为常见措施分类整理： 一、技术防护措施华途加密技术文件加密：使用AES、RSA等算法对敏感文件加密。传输加密：通过SSL/TLS、VPN保障传输安全，禁止明文传…...

编程日记 2025/6/24 4:08:22

C++ Mac 打包运行方案(cmake)

文章目录背景动态库梳理打包方案静态库处理动态库处理(PCL库)编译链接动态库后处理逻辑批量信任背景使用C编写的一个小项目，需要打包成mac下的可执行文件（免安装版本），方便分发给其他mac执行，需要把项目的动态库都…...

编程日记 2025/6/24 17:51:10

数学复习笔记 10

前言我觉得数学的高分乃至满分属于那些，聪明，坚韧，勇敢，细致的人。我非常惭愧自己不是这样的人，我在生活中发现了这样的同学，和他们交流的时候我常常感到汗流浃背，因为他们非常扎实的基础知识…...

编程日记 2025/6/24 9:09:17

Oracle-相关笔记

Oracle Database Online Documentation 11g 连接 WinR sqlplus username/passwordhostname:port/service_namesqlplus user02/123456192.xxx:1521/orclsqlplus / as sysdba #SQL*Plus 終端编码使用UTF-8 chcp 65001#打开SQL*Plus程序 sqlplus /nolog#使用dba角色登录(用 1.…...

编程日记 2025/6/22 17:16:10

mac安装cast

背景 pycharm本地运行脚本时提示cast没有安装问题原因脚本尝试调用cast命令（以太坊开发工具foundry中的子命令），但您的系统未安装该工具。从日志可见，错误发生在通过sysutil.py执行shell命令时。解决方案方法1&#xf…...

编程日记 2025/6/21 1:41:14

CodeEdit：macOS上一款可以让Xcode退休的IDE

CodeEdit 是一款轻量级、原生构建的代码编辑器，完全免费且开源。它使用纯 swift 实现，而且专为 macOS 设计，旨在为开发者提供更高效、更可靠的编程环境，同时释放 Mac 的全部潜力。 Stars 数21,719Forks 数1,081 主要特点 macOS 原…...

编程日记 2025/6/25 13:46:12

opencv4.11编译Debug提示缺少python312_d.lib或python3*_d.lib的解决办法

前言当我们编译OpenCV 4.11的时候可能会遇到提示缺少库文件，这个时候我们可以下载Python源码编译这个lib。也可以下载我上传的版本（python312_d.lib），但是如果是其他版本需要自己编译。编译步骤如下，大概几分钟搞定…...

编程日记 2025/6/22 9:52:23

html的鼠标点击事件有哪些写法

在HTML中，鼠标点击事件的实现方式多样，以下从基础语法到现代实践为您详细梳理： 一、基础写法：直接内联事件属性在HTML标签内通过on前缀事件属性绑定处理函数，适合简单交互场景： …...

编程日记 2025/6/23 18:51:37

深度解析物理机服务器故障修复时间：影响因素与优化策略

一、物理机故障修复的核心影响因素物理机作为企业 IT 基础设施的核心载体，其故障修复效率直接关系到业务连续性。故障修复时间（MTTR）受多重因素交叉影响： 1. 故障类型的复杂性硬件级故障： 简单故障：内存…...

编程日记 2025/6/25 8:19:15

蓝桥杯 2024 C++国 B最小字符串

P10910 [蓝桥杯 2024 国 B] 最小字符串题目描述给定一个长度为 N N N 且只包含小写字母的字符串 S S S，和 M M M 个小写字母 c 1 , c 2 , ⋯ , c M c_1, c_2, \cdots, c_M c1,c2,⋯,cM。现在你要把 M M M 个小写字母全部插入到字符串 S S S 中&…...

编程日记 2025/6/25 13:50:24

解密企业级大模型智能体Agentic AI 关键技术：MCP、A2A、Reasoning LLMs-docker MCP解析

解密企业级大模型智能体Agentic AI 关键技术：MCP、A2A、Reasoning LLMs-docker MCP解析这里面有很重要的原因其中一个很其中一个原因是因为如果你使用docker的方式，你可以在虚拟环境下就类似于这个沙箱的这个机制可以进行隔离。这对于安全，…...

编程日记 2025/6/20 5:30:19

访问 Docker 官方镜像源（包括代理）全部被“重置连接”或超时

华为云轻量应用服务器（Ubuntu 系统） 遇到的问题是： 🔒 访问 Docker 官方镜像源（包括代理）全部被“重置连接”或超时了，说明你这台服务器的出境网络对这些国外域名限制很严格，常见于华…...

编程日记 2025/6/22 7:14:06

前馈神经网络回归(ANN Regression)从原理到实战

前馈神经网络回归(ANN Regression)从原理到实战一、回归问题与前馈神经网络的适配性分析在机器学习领域，回归任务旨在建立输入特征与连续型输出变量之间的映射关系。前馈神经网络（Feedforward Neural Network）作为最基础的神经网络架构&a…...

编程日记 2025/6/24 15:20:45

RNN/LSTM原理与 PyTorch 时间序列预测实战

🕰️ RNN / LSTM 原理与 PyTorch 时间序列预测实战在处理时间序列数据、语音信号、文本序列等连续性强的问题时，循环神经网络（RNN）及其改进版本 LSTM（长短期记忆网络）是最常见也最有效的模型之一。本文将深入讲解 RNN 和 LSTM 的核心原理，并通过 PyTorch 实现一个时间…...

编程日记 2025/6/1 16:05:22

Docker容器镜像与容器常用操作指南

一、镜像基础操作搜索镜像 docker search <镜像名>在Docker Hub中查找公开镜像，例如： docker search nginx拉取镜像 docker pull <镜像名>:<标签>从仓库拉取镜像到本地，标签默认为latest： docker pull nginx:a…...

编程日记 2025/6/24 1:48:09

1：OpenCV—图像基础

OpenCV教程头文件您只需要在程序中包含 opencv2/opencv.hpp 头文件。该头文件将包含应用程序的所有其他必需头文件。因此，您不再需要费心考虑程序应包含哪些头文件。例如 - #include <opencv2/opencv.hpp>命名空间所有 OpenCV 类和函数都在 cv 命名空…...

编程日记 2025/6/21 17:58:36

测试--BUG(软件测试⽣命周期 bug的⽣命周期与开发产⽣争执怎么办)

1. 软件测试的⽣命周期软件测试贯穿于软件的整个⽣命周期，针对这句话我们⼀起来看⼀下软件测试是如何贯穿软件的整个⽣命周期。软件测试的⽣命周期是指测试流程，这个流程是按照⼀定顺序执⾏的⼀系列特定的步骤，去保证产品质量符合需求。在软…...

编程日记 2025/6/22 12:40:58

基于大模型预测围术期麻醉苏醒时间的技术方案

目录一、数据收集与处理（一）数据来源（二）数据预处理二、大模型构建与训练（一）模型选择（二）模型训练三、围术期麻醉苏醒时间预测（一）术前预测（二）术中动态预测四、并发症风险预测（一）风险因素分析（二）风险预测模型五、基于预测制定手术方案（一）个性化手术规划…...

编程日记 2025/6/23 22:11:10

QT6 源（101）阅读与注释 QPlainTextEdit，其继承于QAbstractScrollArea，属性学习与测试

（1） （2） （3）属性学习与测试 ： （4） （5） 谢谢...

编程日记 2025/6/24 23:11:26

电池组PACK自动化生产线：多领域电池生产的“智能引擎”

在电池产业蓬勃发展的当下，电池组PACK自动化生产线凭借其高效、精准、智能的优势，成为众多电池生产领域的核心装备。它广泛适用于数码电池、工具电池、储能电池、电动车电池以及动力电池的生产，有力推动了相关产业的升级与发展。数码电池领…...

编程日记 2025/6/23 6:32:21

生成式AI在编程中的应用场景：从代码生成到安全检测

引言生成式AI正在深刻改变软件开发的方式，从代码编写到测试、文档和维护，AI技术正在为每个环节带来革命性的变革。本文将深入探讨生成式AI在编程中的主要应用场景，分析其优势与局限性，并展望未来发展趋势。主要应用场景 1. 代…...

编程日记 2025/6/24 20:24:35

安全牛报告解读《低空经济发展白皮书（3.0）安全体系》

一、概述《低空经济发展白皮书（3.0）安全体系》由粤港澳大湾区数字经济研究院（IDEA研究院）发布，旨在构建低空经济安全发展的系统性框架，解决规模化低空飞行中的安全挑战。核心目标是明确安全体系需覆盖的飞…...

编程日记 2025/6/24 6:17:07

“2W2H”分析方法

“2W2H”是一种常用的分析方法，它通过回答**What（是什么）、Why（为什么）、How（怎么做）、How much（多少）**这四个问题来全面了解和分析一个事物或问题。这种方法可以帮助你…...

编程日记 2025/6/22 18:52:32

【数据挖掘笔记】兴趣度度量Interest of an association rule

在数据挖掘中，关联规则挖掘是一个重要的任务。兴趣度度量是评估关联规则的重要指标，以下是三个常用的兴趣度度量：支持度、置信度和提升度。支持度（Support） 计算方法支持度表示包含项集的事务占总事务的比例&…...

编程日记 2025/6/23 19:20:36

ArcGIS Pro调用多期历史影像

一、访问World Imagery Wayback，基本在我国范围如下图： 二、放大到您感兴趣的区域三、查看影像版本信息点击第二步的按钮后，便可跳转至World Imagery (Wayback 2025-04-24)的相关信息。四、点击上图影像版本信息，页面跳转…...

编程日记 2025/6/25 5:56:05

Web3.0：互联网的去中心化未来

随着互联网技术的不断发展，我们正站在一个新时代的门槛上——Web3.0时代。Web3.0不仅仅是一个技术升级，它更是一种全新的互联网理念，旨在通过去中心化技术重塑网络世界。本文将深入探讨Web3.0的核心概念、技术基础、应用场景以及它对未来的深…...

编程日记 2025/6/2 14:37:42

java17

1.常见API之BigDecimal 底层存储方式： 2.如何分辨过时代码： 有横线的代码表示该代码已过时 3.正则表达式之字符串匹配注意：如果X不是单一字符，需要加[]中括号注意：1.想要表达正则表达式里面的.需要\\. 2.想要表…...

编程日记 2025/6/24 22:41:03

游戏引擎学习第283天:“让‘Standing-on’成为一个更严谨的概念

如果同时使用多个OpenGL上下文，并且它们都有工作负载，GPU或GPU驱动程序如何决定调度这些工作？我注意到Windows似乎优先处理活动窗口的OpenGL上下文（即活动窗口表现更好），挺有意思的…… 当多个OpenGL上下文…...

编程日记 2025/6/24 21:27:34

小白上手RPM包制作

目录 rpm常用命令安装环境-Ruby 安装环境-fpm 关于服务器打包-打包二进制工程 .fpm配置文件打包-打没有文件的包 RPM 包微调命令行参数 fpm --help RPM 签名打包-制作NGINX的RPM包关于rpmbuild 简单使用打包之前的准备工作 rpmbuild 打包 - sniproxy …...

编程日记 2025/6/24 7:19:50

电商热销榜的5种实现方案

文章目录 1. MySQL 聚合查询：传统统计法2. Redis Sorted Set：内存排行榜3. Elasticsearch 实时聚合：搜索专家4. 缓存异步更新：榜单的幕后推手5. 大数据离线批处理：夜间魔法师博主介绍：全网粉丝10w、CSDN合…...

编程日记 2025/6/22 20:18:27

车载诊断进阶篇 --- 车载诊断概念

我是穿拖鞋的汉子，魔都中坚持长期主义的汽车电子工程师。老规矩，分享一段喜欢的文字，避免自己成为高知识低文化的工程师：钝感力的“钝”，不是木讷、迟钝，而是直面困境的韧劲和耐力，是面对外界噪音的通透淡然。生活中有两种人，一种人格外在意别人的眼光;另一种人无论…...

编程日记 2025/6/24 1:31:08

AD 多层线路及装配图PDF的输出

装配图的输出： 1.点开‘智能PDF’ 2. 设置显示顶层： 设置显示底层： 多层线路的输出同样使用‘智能PDF’...

编程日记 2025/6/3 21:42:13

一、回顾定点数知识点

——定点小数机器码表示

——定点整数机器码表示

——【原码】和【移码】的作用

二、浮点数表示

1、概念引入

2、二进制浮点数的“科学计算法”公式

实际上，准确的公式应该是

总结：

3、浮点数机器码规则

1）浮点数机器码的组成

2）求阶码的公式

3）浮点数和真值之间转换

【浮点数真值——>浮点数机器码】

【浮点数机器码——>浮点数真值】

4）浮点数机器码可表示范围

4、普通浮点数规格化

1）为什么规格化

2）怎么规格化

具体措施：【左规】和【右规】

规格化后的机器码尾码是啥样的？

补充：不同基数r，会导致不同的规格化

3）例题

5、IEEE 754规范

1）表示规则

2）IEEE754浮点数机器码和真值的转换

【浮点数机器码——>浮点数真值】

【浮点数真值——>浮点数机器码】

3）IEEE754浮点数机器码可表示范围

【规格化情况】：整数部分是1，值 = 1 + 小数部分

【正数情况】

【负数情况】

【非规格化情况】：

【正数情况】

【负数情况】

4）解惑：为什么IEEE754的阶码是移码，但不能和补码转换再求真值？

5）IEEE754规格化

6）需要死记硬背的知识点

7）转换类型例题

8）范围类型例题

浮点数运算我在下一篇文章讲

相关文章：