无人机避障——如何利用MinumSnap进行对速度、加速度进行优化的轨迹生成(附C++python代码)
🔥轨迹规划领域的 “YYDS”——minimum snap!作为基于优化的二次规划经典,它是无人机、自动驾驶轨迹规划论文必引的 “开山之作”。从优化目标函数到变量曲线表达,各路大神疯狂 “魔改”,衍生出无数创新方案。
💡深度剖析百度 Apollo 的迭代奥秘:早期五次多项式拼接,如今离散点 piecewise jerk 路径 / 速度规划,本质皆是 minimum snap 的 “变形记”。
🚀想知道这些 “神操作” 背后的数学逻辑与技术细节?想解锁轨迹规划的优化新姿势?速来围观,带你直击前沿技术内核,开启轨迹规划的 “脑洞大开” 之旅!
问题:局部路径在运行的过程中对当下的速度和加速度进行采样,得到一个经过速度和加速度优化的轨迹进行运行是非常必要的,可以减少无人机单单用基于位置的简单的路径在空中经过PID或者其他控制以后出现振荡与大量抖动,这部分与控制并无关系,因为是期望都会不稳定,所以需要MinumSnap采用最小加加加速度(snap)的方法进行优化轨迹生成。
Fast-planner的全局规划主函数:
// 全局轨迹规划主函数,输入参数为起始位置
bool FastPlannerManager::planGlobalTraj(const Eigen::Vector3d& start_pos) {// 清空之前的拓扑路径数据plan_data_.clearTopoPaths();/* ------------------------- 全局参考轨迹生成 ------------------------- */// 获取预定义的全局航点vector<Eigen::Vector3d> points = plan_data_.global_waypoints_;if (points.size() == 0) std::cout << "no global waypoints!" << std::endl; // 空航点警告// 将起始点插入航点列表首部(确保轨迹从当前位置开始)points.insert(points.begin(), start_pos);/* ----------- 插入中间点(当航点间距过大时分段插入) ----------- */vector<Eigen::Vector3d> inter_points;const double dist_thresh = 4.0; // 最大分段距离阈值for (int i = 0; i < points.size() - 1; ++i) {inter_points.push_back(points.at(i)); // 添加当前航点double dist = (points.at(i + 1) - points.at(i)).norm();// 当两点间距超过阈值时插入中间点if (dist > dist_thresh) {int id_num = floor(dist / dist_thresh) + 1; // 计算需要插入的中间点数// 线性插值生成中间点(例如间距6米时插入1个中间点,形成3段)for (int j = 1; j < id_num; ++j) {Eigen::Vector3d inter_pt = points.at(i) * (1.0 - double(j)/id_num) + points.at(i + 1) * double(j)/id_num;inter_points.push_back(inter_pt);}}}inter_points.push_back(points.back()); // 添加最后一个航点// 若处理后仅有起点和终点,在中间强制添加中点(确保轨迹有控制点)if (inter_points.size() == 2) {Eigen::Vector3d mid = (inter_points[0] + inter_points[1]) * 0.5;inter_points.insert(inter_points.begin() + 1, mid);}/* ------------------------- 轨迹生成 ------------------------- */// 构造位置矩阵,每行代表一个航点的3D坐标int pt_num = inter_points.size();Eigen::MatrixXd pos(pt_num, 3);for (int i = 0; i < pt_num; ++i) pos.row(i) = inter_points[i];// 初始化速度/加速度边界条件为零(起点终点零速度、零加速度)Eigen::Vector3d zero(0, 0, 0);// 计算相邻航点间的预估时间(基于最大速度和距离)Eigen::VectorXd time(pt_num - 1);for (int i = 0; i < pt_num - 1; ++i) {time(i) = (pos.row(i+1) - pos.row(i)).norm() / pp_.max_vel_;}// 调整首尾段时间权重(确保时间不小于1秒)time(0) *= 2.0;time(0) = max(1.0, time(0));time(time.rows()-1) *= 2.0;time(time.rows()-1) = max(1.0, time(time.rows()-1));// 生成最小加加速度(Snap)多项式轨迹PolynomialTraj gl_traj = minSnapTraj(pos, zero, zero, zero, zero, time);// 设置全局轨迹数据并记录生成时间auto time_now = ros::Time::now();global_data_.setGlobalTraj(gl_traj, time_now);/* ------------------------- 局部轨迹截取 ------------------------- */double dt, duration;// 重新参数化局部轨迹(时间间隔dt和总时长duration会被计算)Eigen::MatrixXd ctrl_pts = reparamLocalTraj(0.0, dt, duration);// 基于控制点生成3阶非均匀B样条轨迹NonUniformBspline bspline(ctrl_pts, 3, dt);// 更新局部轨迹数据global_data_.setLocalTraj(bspline, 0.0, duration, 0.0);local_data_.position_traj_ = bspline;local_data_.start_time_ = time_now;ROS_INFO("global trajectory generated.");// 更新轨迹信息(如速度、加速度约束等)updateTrajInfo();return true;
}改变最大分段距离阈值dist_thresh:
改变前:
dist_thresh = 4.0
改变后:
dist_thresh = 20.0 【注意】:运行之后发现并没有太大的区别。
【注意】:运行之后发现并没有太大的区别。
最小化Sanp轨迹生成函数(核心实现)解读——函数minSnapTraj:
// 最小Snap轨迹生成函数(核心实现)
PolynomialTraj minSnapTraj(const Eigen::MatrixXd& Pos, const Eigen::Vector3d& start_vel,const Eigen::Vector3d& end_vel, const Eigen::Vector3d& start_acc,const Eigen::Vector3d& end_acc, const Eigen::VectorXd& Time) {// --- 初始化阶段 --- int seg_num = Time.size(); // 轨迹段数(航点间分段)Eigen::MatrixXd poly_coeff(seg_num, 3 * 6); // 存储XYZ三轴各6阶多项式系数Eigen::VectorXd Px(6 * seg_num), Py(6 * seg_num), Pz(6 * seg_num); // 各段多项式系数向量int num_f, num_p; // number of fixed and free variablesint num_d; // number of all segments' derivatives// 阶乘计算lambda(用于导数项系数计算)const static auto Factorial = [](int x) {int fac = 1;for (int i = x; i > 0; i--)fac = fac * i;return fac;};/* ---------- end point derivative ---------- */// --- 端点导数约束设置 ---Eigen::VectorXd Dx = Eigen::VectorXd::Zero(seg_num * 6); // X轴各段导数约束Eigen::VectorXd Dy = Eigen::VectorXd::Zero(seg_num * 6);Eigen::VectorXd Dz = Eigen::VectorXd::Zero(seg_num * 6);for (int k = 0; k < seg_num; k++) {/* position to derivative */// 设置位置约束(每段起点和终点)Dx(k * 6) = Pos(k, 0);Dx(k * 6 + 1) = Pos(k + 1, 0);Dy(k * 6) = Pos(k, 1);Dy(k * 6 + 1) = Pos(k + 1, 1);Dz(k * 6) = Pos(k, 2);Dz(k * 6 + 1) = Pos(k + 1, 2);// 首段设置初始速度/加速度约束if (k == 0) {Dx(k * 6 + 2) = start_vel(0);Dy(k * 6 + 2) = start_vel(1);Dz(k * 6 + 2) = start_vel(2);Dx(k * 6 + 4) = start_acc(0);Dy(k * 6 + 4) = start_acc(1);Dz(k * 6 + 4) = start_acc(2);} // 末段设置终止速度/加速度约束else if (k == seg_num - 1) {Dx(k * 6 + 3) = end_vel(0);Dy(k * 6 + 3) = end_vel(1);Dz(k * 6 + 3) = end_vel(2);Dx(k * 6 + 5) = end_acc(0);Dy(k * 6 + 5) = end_acc(1);Dz(k * 6 + 5) = end_acc(2);}}/* ---------- Mapping Matrix A ---------- */// --- 构建映射矩阵A ---Eigen::MatrixXd Ab;Eigen::MatrixXd A = Eigen::MatrixXd::Zero(seg_num * 6, seg_num * 6);for (int k = 0; k < seg_num; k++) {Ab = Eigen::MatrixXd::Zero(6, 6);for (int i = 0; i < 3; i++) {Ab(2 * i, i) = Factorial(i);for (int j = i; j < 6; j++)Ab(2 * i + 1, j) = Factorial(j) / Factorial(j - i) * pow(Time(k), j - i);}A.block(k * 6, k * 6, 6, 6) = Ab;}/* ---------- Produce Selection Matrix C' ---------- */// --- 构建选择矩阵Ct ---Eigen::MatrixXd Ct, C;num_f = 2 * seg_num + 4; // 3 + 3 + (seg_num - 1) * 2 = 2m + 4num_p = 2 * seg_num - 2; //(seg_num - 1) * 2 = 2m - 2num_d = 6 * seg_num;Ct = Eigen::MatrixXd::Zero(num_d, num_f + num_p);Ct(0, 0) = 1;Ct(2, 1) = 1;Ct(4, 2) = 1; // stack the start pointCt(1, 3) = 1;Ct(3, 2 * seg_num + 4) = 1;Ct(5, 2 * seg_num + 5) = 1;Ct(6 * (seg_num - 1) + 0, 2 * seg_num + 0) = 1;Ct(6 * (seg_num - 1) + 1, 2 * seg_num + 1) = 1; // Stack the end pointCt(6 * (seg_num - 1) + 2, 4 * seg_num + 0) = 1;Ct(6 * (seg_num - 1) + 3, 2 * seg_num + 2) = 1; // Stack the end pointCt(6 * (seg_num - 1) + 4, 4 * seg_num + 1) = 1;Ct(6 * (seg_num - 1) + 5, 2 * seg_num + 3) = 1; // Stack the end pointfor (int j = 2; j < seg_num; j++) {Ct(6 * (j - 1) + 0, 2 + 2 * (j - 1) + 0) = 1;Ct(6 * (j - 1) + 1, 2 + 2 * (j - 1) + 1) = 1;Ct(6 * (j - 1) + 2, 2 * seg_num + 4 + 2 * (j - 2) + 0) = 1;Ct(6 * (j - 1) + 3, 2 * seg_num + 4 + 2 * (j - 1) + 0) = 1;Ct(6 * (j - 1) + 4, 2 * seg_num + 4 + 2 * (j - 2) + 1) = 1;Ct(6 * (j - 1) + 5, 2 * seg_num + 4 + 2 * (j - 1) + 1) = 1;}C = Ct.transpose();Eigen::VectorXd Dx1 = C * Dx;Eigen::VectorXd Dy1 = C * Dy;Eigen::VectorXd Dz1 = C * Dz;/* ---------- minimum snap matrix ---------- */// --- 构造最小Snap优化问题 ---Eigen::MatrixXd Q = Eigen::MatrixXd::Zero(seg_num * 6, seg_num * 6);// 计算Snap项积分(四阶导数平方的积分)for (int k = 0; k < seg_num; k++) {for (int i = 3; i < 6; i++) {for (int j = 3; j < 6; j++) {Q(k * 6 + i, k * 6 + j) =i * (i - 1) * (i - 2) * j * (j - 1) * (j - 2) / (i + j - 5) * pow(Time(k), (i + j - 5));}}}/* ---------- R matrix ---------- */// --- 求解闭式解 ---Eigen::MatrixXd R = C * A.transpose().inverse() * Q * A.inverse() * Ct;Eigen::VectorXd Dxf(2 * seg_num + 4), Dyf(2 * seg_num + 4), Dzf(2 * seg_num + 4);Dxf = Dx1.segment(0, 2 * seg_num + 4);Dyf = Dy1.segment(0, 2 * seg_num + 4);Dzf = Dz1.segment(0, 2 * seg_num + 4);Eigen::MatrixXd Rff(2 * seg_num + 4, 2 * seg_num + 4);Eigen::MatrixXd Rfp(2 * seg_num + 4, 2 * seg_num - 2);Eigen::MatrixXd Rpf(2 * seg_num - 2, 2 * seg_num + 4);Eigen::MatrixXd Rpp(2 * seg_num - 2, 2 * seg_num - 2);Rff = R.block(0, 0, 2 * seg_num + 4, 2 * seg_num + 4);Rfp = R.block(0, 2 * seg_num + 4, 2 * seg_num + 4, 2 * seg_num - 2);Rpf = R.block(2 * seg_num + 4, 0, 2 * seg_num - 2, 2 * seg_num + 4);Rpp = R.block(2 * seg_num + 4, 2 * seg_num + 4, 2 * seg_num - 2, 2 * seg_num - 2);/* ---------- close form solution ---------- */Eigen::VectorXd Dxp(2 * seg_num - 2), Dyp(2 * seg_num - 2), Dzp(2 * seg_num - 2);Dxp = -(Rpp.inverse() * Rfp.transpose()) * Dxf;Dyp = -(Rpp.inverse() * Rfp.transpose()) * Dyf;Dzp = -(Rpp.inverse() * Rfp.transpose()) * Dzf;Dx1.segment(2 * seg_num + 4, 2 * seg_num - 2) = Dxp;Dy1.segment(2 * seg_num + 4, 2 * seg_num - 2) = Dyp;Dz1.segment(2 * seg_num + 4, 2 * seg_num - 2) = Dzp;Px = (A.inverse() * Ct) * Dx1;Py = (A.inverse() * Ct) * Dy1;Pz = (A.inverse() * Ct) * Dz1;for (int i = 0; i < seg_num; i++) {poly_coeff.block(i, 0, 1, 6) = Px.segment(i * 6, 6).transpose();poly_coeff.block(i, 6, 1, 6) = Py.segment(i * 6, 6).transpose();poly_coeff.block(i, 12, 1, 6) = Pz.segment(i * 6, 6).transpose();}/* ---------- use polynomials ---------- */PolynomialTraj poly_traj;for (int i = 0; i < poly_coeff.rows(); ++i) {vector<double> cx(6), cy(6), cz(6);for (int j = 0; j < 6; ++j) {cx[j] = poly_coeff(i, j), cy[j] = poly_coeff(i, j + 6), cz[j] = poly_coeff(i, j + 12);}reverse(cx.begin(), cx.end());reverse(cy.begin(), cy.end());reverse(cz.begin(), cz.end());double ts = Time(i);poly_traj.addSegment(cx, cy, cz, ts);}return poly_traj;
}函数定义和输入变量部分:
PolynomialTraj minSnapTraj(const Eigen::MatrixXd& Pos, const Eigen::Vector3d& start_vel,const Eigen::Vector3d& end_vel, const Eigen::Vector3d& start_acc,const Eigen::Vector3d& end_acc, const Eigen::VectorXd& Time) {定义轨迹段数,定义进行拟合的多项式:
int seg_num = Time.size(); // 轨迹段数(航点间分段)Eigen::MatrixXd poly_coeff(seg_num, 3 * 6); // 存储XYZ三轴各6阶多项式系数Eigen::VectorXd Px(6 * seg_num), Py(6 * seg_num), Pz(6 * seg_num); // 各段多项式系数向量int num_f, num_p; // number of fixed and free variablesint num_d; // number of all segments' derivatives自定义计算x的阶乘函数:
// 阶乘计算lambda(用于导数项系数计算)const static auto Factorial = [](int x) {int fac = 1;for (int i = x; i > 0; i--)fac = fac * i;return fac;};首末、以及各段的首末端点的硬约束:
// --- 端点导数约束设置 ---Eigen::VectorXd Dx = Eigen::VectorXd::Zero(seg_num * 6); // X轴各段导数约束Eigen::VectorXd Dy = Eigen::VectorXd::Zero(seg_num * 6);Eigen::VectorXd Dz = Eigen::VectorXd::Zero(seg_num * 6);for (int k = 0; k < seg_num; k++) {/* position to derivative */// 设置位置约束(每段起点和终点)Dx(k * 6) = Pos(k, 0);Dx(k * 6 + 1) = Pos(k + 1, 0);Dy(k * 6) = Pos(k, 1);Dy(k * 6 + 1) = Pos(k + 1, 1);Dz(k * 6) = Pos(k, 2);Dz(k * 6 + 1) = Pos(k + 1, 2);// 首段设置初始速度/加速度约束if (k == 0) {Dx(k * 6 + 2) = start_vel(0);Dy(k * 6 + 2) = start_vel(1);Dz(k * 6 + 2) = start_vel(2);Dx(k * 6 + 4) = start_acc(0);Dy(k * 6 + 4) = start_acc(1);Dz(k * 6 + 4) = start_acc(2);} // 末段设置终止速度/加速度约束else if (k == seg_num - 1) {Dx(k * 6 + 3) = end_vel(0);Dy(k * 6 + 3) = end_vel(1);Dz(k * 6 + 3) = end_vel(2);Dx(k * 6 + 5) = end_acc(0);Dy(k * 6 + 5) = end_acc(1);Dz(k * 6 + 5) = end_acc(2);}}构建A矩阵:
// --- 构建映射矩阵A ---Eigen::MatrixXd Ab;Eigen::MatrixXd A = Eigen::MatrixXd::Zero(seg_num * 6, seg_num * 6);for (int k = 0; k < seg_num; k++) {Ab = Eigen::MatrixXd::Zero(6, 6);for (int i = 0; i < 3; i++) {Ab(2 * i, i) = Factorial(i);for (int j = i; j < 6; j++)Ab(2 * i + 1, j) = Factorial(j) / Factorial(j - i) * pow(Time(k), j - i);}A.block(k * 6, k * 6, 6, 6) = Ab;}【注意】:A矩阵的构建与阶数有关,跟时间Time有关,它是由于微分约束的原因,但是我们并没有限制轨迹必须通过某一些点,或者以一个确定的状态通过某一些中间的航迹点。也就是上述的这些多项式系数中,有一些是已知的。但是大多数情况下,我们都是对轨迹的位置有一些限制的,并不能随意生成,所以还需要给中间的航迹点加一些限制。包括位置、速度、加速度、Jerk、Snap等等的限制。
可以参考博客:【附源码和详细的公式推导】Minimum Snap轨迹生成,闭式求解Minimum Snap问题,机器人轨迹优化,多项式轨迹路径生成与优化-CSDN博客
构建C矩阵:
// --- 构建选择矩阵Ct ---Eigen::MatrixXd Ct, C;num_f = 2 * seg_num + 4; // 3 + 3 + (seg_num - 1) * 2 = 2m + 4num_p = 2 * seg_num - 2; //(seg_num - 1) * 2 = 2m - 2num_d = 6 * seg_num;Ct = Eigen::MatrixXd::Zero(num_d, num_f + num_p);
// 固定约束部分(起点终点位置速度加速度)Ct(0, 0) = 1;Ct(2, 1) = 1;Ct(4, 2) = 1; // stack the start pointCt(1, 3) = 1;Ct(3, 2 * seg_num + 4) = 1;Ct(5, 2 * seg_num + 5) = 1;Ct(6 * (seg_num - 1) + 0, 2 * seg_num + 0) = 1;Ct(6 * (seg_num - 1) + 1, 2 * seg_num + 1) = 1; // Stack the end pointCt(6 * (seg_num - 1) + 2, 4 * seg_num + 0) = 1;Ct(6 * (seg_num - 1) + 3, 2 * seg_num + 2) = 1; // Stack the end pointCt(6 * (seg_num - 1) + 4, 4 * seg_num + 1) = 1;Ct(6 * (seg_num - 1) + 5, 2 * seg_num + 3) = 1; // Stack the end point
// ...(中间段连续性约束填充)for (int j = 2; j < seg_num; j++) {Ct(6 * (j - 1) + 0, 2 + 2 * (j - 1) + 0) = 1;Ct(6 * (j - 1) + 1, 2 + 2 * (j - 1) + 1) = 1;Ct(6 * (j - 1) + 2, 2 * seg_num + 4 + 2 * (j - 2) + 0) = 1;Ct(6 * (j - 1) + 3, 2 * seg_num + 4 + 2 * (j - 1) + 0) = 1;Ct(6 * (j - 1) + 4, 2 * seg_num + 4 + 2 * (j - 2) + 1) = 1;Ct(6 * (j - 1) + 5, 2 * seg_num + 4 + 2 * (j - 1) + 1) = 1;}C = Ct.transpose();Eigen::VectorXd Dx1 = C * Dx;Eigen::VectorXd Dy1 = C * Dy;Eigen::VectorXd Dz1 = C * Dz;【注意】 :C矩阵是希望在A矩阵的基础上,加入连续性约束,使得微分约束和连续性约束成为一个整体,它是由于每一段轨迹与下一段轨迹需要连续性约束,也就是导数需要限制中间的航迹点在两段轨迹的接合处是左右两边状态要连续。如果我们要最小化的目标是Jerk,那么我们必须保证接合处三阶导数是连续的。
构建最小Snap优化问题,即QP问题:
// --- 构造最小Snap优化问题 ---Eigen::MatrixXd Q = Eigen::MatrixXd::Zero(seg_num * 6, seg_num * 6);// 计算Snap项积分(四阶导数平方的积分)for (int k = 0; k < seg_num; k++) {for (int i = 3; i < 6; i++) {for (int j = 3; j < 6; j++) {Q(k * 6 + i, k * 6 + j) =i * (i - 1) * (i - 2) * j * (j - 1) * (j - 2) / (i + j - 5) * pow(Time(k), (i + j - 5));}}}【注意】:也就是QP问题,Q矩阵只与时间Time有关,其余的就是跟多项式系数有一定的关系。
闭式求解:
// --- 求解闭式解 ---Eigen::MatrixXd R = C * A.transpose().inverse() * Q * A.inverse() * Ct;Eigen::VectorXd Dxf(2 * seg_num + 4), Dyf(2 * seg_num + 4), Dzf(2 * seg_num + 4);Dxf = Dx1.segment(0, 2 * seg_num + 4);Dyf = Dy1.segment(0, 2 * seg_num + 4);Dzf = Dz1.segment(0, 2 * seg_num + 4);Eigen::MatrixXd Rff(2 * seg_num + 4, 2 * seg_num + 4);Eigen::MatrixXd Rfp(2 * seg_num + 4, 2 * seg_num - 2);Eigen::MatrixXd Rpf(2 * seg_num - 2, 2 * seg_num + 4);Eigen::MatrixXd Rpp(2 * seg_num - 2, 2 * seg_num - 2);Rff = R.block(0, 0, 2 * seg_num + 4, 2 * seg_num + 4);Rfp = R.block(0, 2 * seg_num + 4, 2 * seg_num + 4, 2 * seg_num - 2);Rpf = R.block(2 * seg_num + 4, 0, 2 * seg_num - 2, 2 * seg_num + 4);Rpp = R.block(2 * seg_num + 4, 2 * seg_num + 4, 2 * seg_num - 2, 2 * seg_num - 2);/* ---------- close form solution ---------- */Eigen::VectorXd Dxp(2 * seg_num - 2), Dyp(2 * seg_num - 2), Dzp(2 * seg_num - 2);Dxp = -(Rpp.inverse() * Rfp.transpose()) * Dxf;Dyp = -(Rpp.inverse() * Rfp.transpose()) * Dyf;Dzp = -(Rpp.inverse() * Rfp.transpose()) * Dzf;Dx1.segment(2 * seg_num + 4, 2 * seg_num - 2) = Dxp;Dy1.segment(2 * seg_num + 4, 2 * seg_num - 2) = Dyp;Dz1.segment(2 * seg_num + 4, 2 * seg_num - 2) = Dzp;
【注意】:根据QP问题,和数学性质,可以通过转化为无约束的最优化问题进行求解,就叫闭式求解。
重新构建多项式系数:
Px = (A.inverse() * Ct) * Dx1;Py = (A.inverse() * Ct) * Dy1;Pz = (A.inverse() * Ct) * Dz1;for (int i = 0; i < seg_num; i++) {poly_coeff.block(i, 0, 1, 6) = Px.segment(i * 6, 6).transpose();poly_coeff.block(i, 6, 1, 6) = Py.segment(i * 6, 6).transpose();poly_coeff.block(i, 12, 1, 6) = Pz.segment(i * 6, 6).transpose();}重新构建轨迹对象:
/* ---------- use polynomials ---------- */PolynomialTraj poly_traj;for (int i = 0; i < poly_coeff.rows(); ++i) {vector<double> cx(6), cy(6), cz(6);for (int j = 0; j < 6; ++j) {cx[j] = poly_coeff(i, j), cy[j] = poly_coeff(i, j + 6), cz[j] = poly_coeff(i, j + 12);}reverse(cx.begin(), cx.end());reverse(cy.begin(), cy.end());reverse(cz.begin(), cz.end());double ts = Time(i);poly_traj.addSegment(cx, cy, cz, ts);}return poly_traj;
}以上为fast-planner中Minum-snap的解析,代码为C++版本的,为了更好的进行迁移,接下来介绍python版本的Minnum-snap库算法。
python中的Minsnap轨迹规划代码库
官网:minsnap-trajectories · PyPI
类似于differential flatness, minimum snap, path planning, trajectory generation相关的轨迹生成python代码其中均可以实现。
由于上述代码库不好使用,遂找到了开源的手搓的三维Minsnap相关python代码,并进行了整理:
最小化Snap的结果:
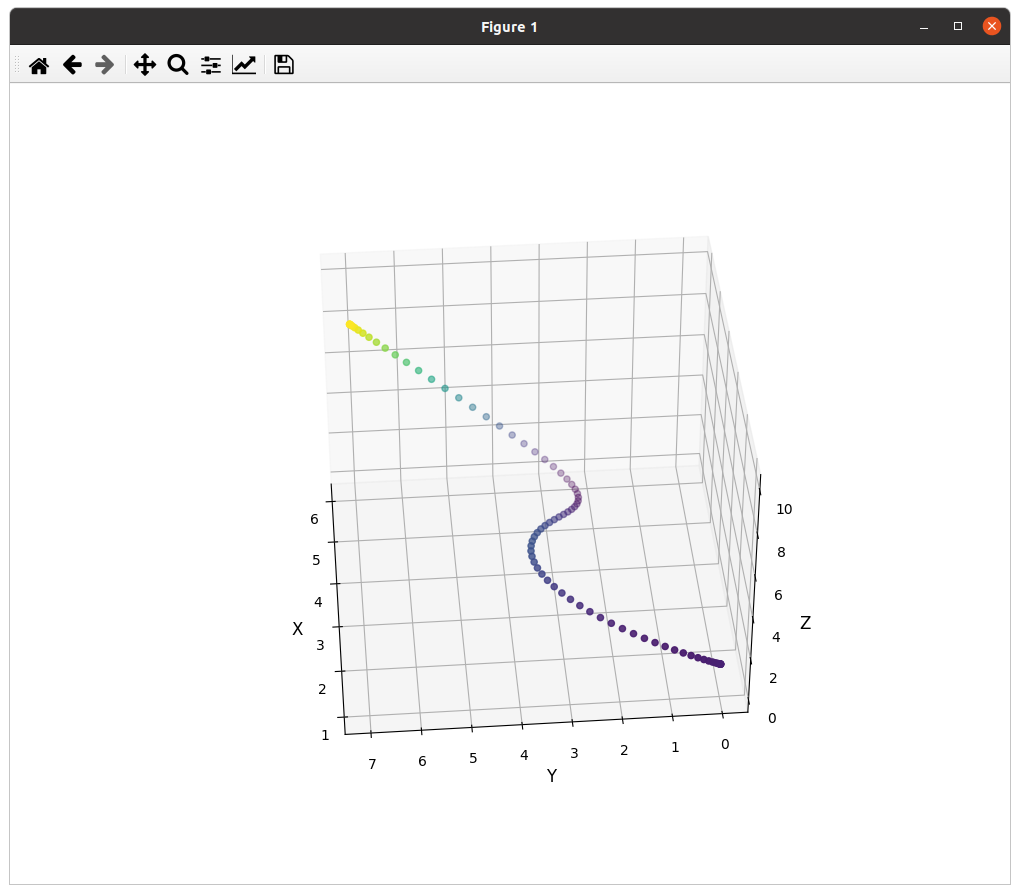
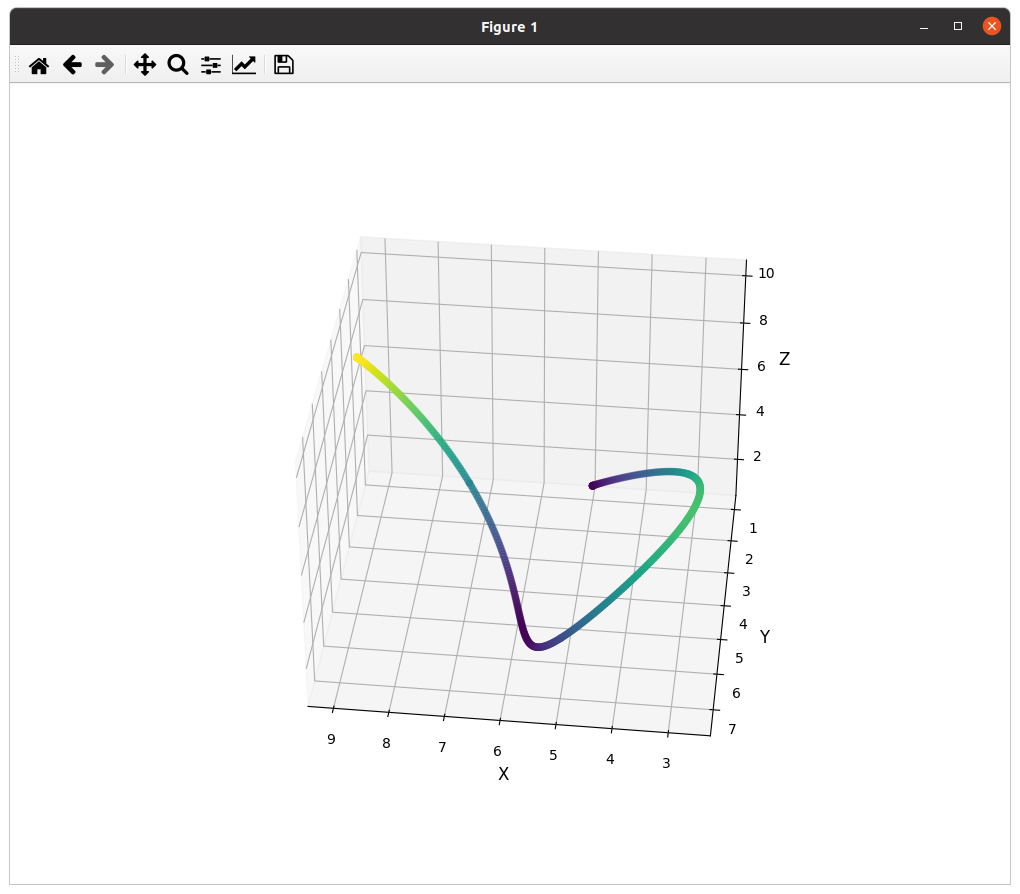
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from cvxopt import matrix, solvers
import open3d as o3d
from scipy.interpolate import splprep, splev,splder
import gurobipy as gpclass TrajectoryPlanner:_instance = Nonedef __new__(cls):if cls._instance is None:cls._instance = super(TrajectoryPlanner, cls).__new__(cls)cls._instance.__initialized = Falsereturn cls._instancedef __init__(self):if self.__initialized:returnself.__initialized = True# 设置numpy打印参数:完全显示数组/禁止科学计数法/每行显示100字符np.set_printoptions(threshold=np.inf, suppress=True, linewidth=100)# 新增全局约束参数(单位:m/s, m/s²)self.MAX_VEL = 2.0 # 最大速度self.MIN_VEL = -2.0 # 最小速度(允许倒车时设为负值)self.MAX_ACC = 2.0 # 最大加速度self.MIN_ACC = -2.0 # 最小加速度(制动限制)self.deltaT = 0.5 #默认时间间隔def farthest_point_sampling(self,points, n_samples):indices = np.zeros(n_samples, dtype=int)distances = np.full(points.shape[0], np.inf)start_idx = np.random.randint(len(points))for i in range(n_samples):indices[i] = start_idxdist = np.linalg.norm(points - points[start_idx], axis=1)distances = np.minimum(distances, dist)start_idx = np.argmax(distances)return points[indices]def build_velocity_constraint_row(self, k, t, N):row = np.zeros(N)coeff = [0, 1, 2*t, 3*t**2, 4*t**3, 5*t**4, 6*t**5, 7*t**6]row[k*8 : (k+1)*8] = coeffreturn rowdef build_acceleration_constraint_row(self, k, t, N):row = np.zeros(N)coeff = [0, 0, 2, 6*t, 12*t**2, 20*t**3, 30*t**4, 0] # 修正二阶导数项[3]row[k*8 : (k+1)*8] = coeffreturn rowdef getpos(self, x, v_start):"""生成轨迹的最小加加速度(snap)优化路径参数:x : 路径点某一维度的坐标序列返回:Pos, Vel, Acc, Jer : 位置、速度、加速度、加加速度轨迹"""self.deltaT = 0.2print(self.deltaT)T = np.linspace(0, self.deltaT * (len(x) - 1), len(x)) # 时间节点生成# 轨迹参数设置K = 4 # 最小化加加加速度(snap)对应四阶导数n_order = 2 * K - 1 # 多项式阶数(7次多项式)M = int(len(x)) - 1 # 轨迹分段数(路径点数量-1)N = M * (n_order + 1) # 优化变量总维度(每段8个系数)def getQk(T_down, T_up):Q = np.zeros((8, 8))T_up2 = T_up**2T_up3 = T_up**3T_up4 = T_up**4T_up5 = T_up**5T_up6 = T_up**6T_up7 = T_up**7T_down2 = T_down**2T_down3 = T_down**3T_down4 = T_down**4T_down5 = T_down**5T_down6 = T_down**6T_down7 = T_down**7Q[4][5] = 1440 * (T_up2 - T_down2)Q[4][6] = 2880 * (T_up3 - T_down3)Q[4][7] = 5040 * (T_up4 - T_down4)Q[5][6] = 10800 * (T_up4 - T_down4)Q[5][7] = 20160 * (T_up5 - T_down5)Q[6][7] = 50400 * (T_up6 - T_down6)Q = Q + Q.TQ[4][4] = 576 * (T_up - T_down)Q[5][5] = 4800 * (T_up3 - T_down3)Q[6][6] = 25920 * (T_up5 - T_down5)Q[7][7] = 100800 * (T_up7 - T_down7)return Q# 构造全局Q矩阵(块对角矩阵)Q = np.zeros((N, N))for k in range(1, M + 1): # 遍历每个轨迹段Qk = getQk(T[k - 1], T[k])# 块填充策略:每段8x8的Qk矩阵放在对角线位置Q[(8*(k-1)) : (8*k), (8*(k-1)) : (8*k)] = QkQ = Q * 2 # 二次规划标准形式需要乘以1/2,这里提前补偿# 构造等式约束矩阵AA0 = np.zeros((2*K + M - 1, N)) # 起点/终点约束 + 中间点约束b0 = np.zeros(len(A0))# 起点/终点的位置、速度、加速度、加加速度约束for k in range(K): # 0-3阶导数约束for i in range(k, 8): # 多项式系数遍历c = 1for j in range(k):c *= (i - j) # 导数系数计算# 起点速度约束(k=1时)if k == 1:A0[2][i] = c * T[0]**(i - k) # 起点速度行索引2# 填充速度约束值到b0b0[2] = v_start # 起始速度预设值# 起点约束(t=0时各阶导数)A0[0 + k*2][i] = c * T[0]**(i - k)# 终点约束(t=T时各阶导数)A0[1 + k*2][(M-1)*8 + i] = c * T[M]**(i - k)b0[0] = x[0] # 起点位置约束值b0[1] = x[M] # 终点位置约束值# 中间点位置约束for m in range(1, M):for i in range(8):A0[8 + m-1][m*8 + i] = T[m]**i # 时间多项式基函数b0[8 + m-1] = x[m] # 中间点位置约束值# 轨迹段连接处的连续性约束(位置-加加速度连续)A1 = np.zeros(((M-1)*K, N))b1 = np.zeros(len(A1))for m in range(M-1): # 遍历每个连接点for k in range(K): # 0-3阶导数连续for i in range(k, 8): # 多项式系数c = 1for j in range(k):c *= (i - j) # 导数系数乘积index = m*4 + k# 前一段轨迹末状态A1[index][m*8 + i] = c * T[m+1]**(i - k)# 后一段轨迹初状态(符号取反)A1[index][(m+1)*8 + i] = -c * T[m+1]**(i - k)# 合并所有约束条件A = np.vstack((A0, A1))b = np.hstack((b0, b1))# 转换为cvxopt需要的矩阵格式Q_mat = matrix(Q)q_mat = matrix(np.zeros(N))A_mat = matrix(A)b_mat = matrix(b)# 求解二次规划问题(网页7提到的凸优化方法)# result = solvers.qp(Q_mat, q_mat, A=A_mat, b=b_mat)# ============ 求解器调用改造 ============result = solvers.qp(Q_mat, q_mat, A=A_mat, b=b_mat)p_coff = np.asarray(result['x']).flatten() # 获取多项式系数# 轨迹重构与导数计算Pos = []; Vel = []; Acc = []; Jer = []for k in range(M): # 遍历每个轨迹段t = np.linspace(T[k], T[k + 1], 100)t_pos = np.vstack((t**0, t**1, t**2, t**3, t**4, t**5, t**6, t**7))t_vel = np.vstack((t*0, t**0, 2 * t**1, 3 * t**2, 4 * t**3, 5 * t**4, 6*t**5, 7*t**6))t_acc = np.vstack((t*0, t*0, 2 * t**0, 3 * 2 * t**1, 4 * 3 * t**2, 5 * 4 * t**3, 6*5*t**4, 7*6*t**5))t_jer = np.vstack((t*0, t*0, t*0, 3 * 2 * t**0, 4 * 3 *2* t**1, 5 * 4 *3* t**2, 6*5*4*t**3, 7*6*5*t**4))coef = p_coff[k * 8 : (k + 1) * 8]coef = np.reshape(coef, (1, 8))pos = coef.dot(t_pos)vel = coef.dot(t_vel)acc = coef.dot(t_acc)jer = coef.dot(t_jer)Pos.append([t, pos[0]])Vel.append([t, vel[0]])Acc.append([t, acc[0]])Jer.append([t, jer[0]])return np.array(Pos), np.array(Vel), np.array(Acc), np.array(Jer)def merge_axis_data(self, data):"""合并三维轨迹数据为连续时间序列"""time = np.concatenate(data[:, 0, :].T) # 时间轴values = np.concatenate(data[:, 1, :].T) # 数值轴return time, valuesdef smooth_3d_path(self,path, s=1.0):"""三维路径B样条平滑"""path = np.array(path)if len(path) < 10: # 样条需要至少4个点return pathtck, u = splprep(path.T, s=s)if len(path) > 10:num_len = int(len(path)/2)else:num_len = int(len(path))new_points = splev(np.linspace(0,1,num_len), tck)return np.column_stack(new_points)def plot_trajectory(self, path, initial_vel, plot_flag=True):path = np.array(path) # 转换为numpy数组initial_vel = np.array(initial_vel)displacements = np.diff(path, axis=0) # 形状:(N-1, 3) 的位移向量distances = np.linalg.norm(displacements, axis=1) # 沿轴1计算每个向量的范数self.deltaT = np.max(distances) / self.MAX_VELprint(self.deltaT)# 分别处理三个维度的轨迹Posx, Velx, Accx, Jerx = self.getpos(path[:, 0], initial_vel[0]) # X轴轨迹Posy, Vely, Accy, Jery = self.getpos(path[:, 1], initial_vel[1]) # Y轴轨迹Posz, Velz, Accz, Jerz = self.getpos(path[:, 2], initial_vel[2]) # Z轴轨迹# 合并所有轨迹点的三维坐标x = np.concatenate(Posx[:, 1, :].T) # X坐标序列y = np.concatenate(Posy[:, 1, :].T) # Y坐标序列z = np.concatenate(Posz[:, 1, :].T) # Z坐标序列# 将三维坐标组合成一个优化路径optimization_path = np.column_stack((x, y, z))# 如果plot_flag为True,则绘制三维轨迹图if plot_flag:# 三维轨迹可视化fig = plt.figure(figsize=(10, 8))ax = fig.add_subplot(111, projection='3d')# 绘制三维散点图ax.scatter3D(x[::5], y[::5], z[::5], c=z[::5], # 颜色映射Z值cmap='viridis', # 使用viridis色图s=20) # 点的大小# 设置坐标轴标签和观察视角ax.set_xlabel('X', fontsize=12)ax.set_ylabel('Y', fontsize=12)ax.set_zlabel('Z', fontsize=12)ax.view_init(elev=30, azim=45) # 仰角30度,方位角45度# 绘制速度图time_x, vel_x = self.merge_axis_data(Velx)time_y, vel_y = self.merge_axis_data(Vely)time_z, vel_z = self.merge_axis_data(Velz)plt.figure(figsize=(12, 6))plt.scatter(time_x, vel_x, color='red', s=10, label='X', marker='o') # X轴速度点plt.scatter(time_y, vel_y, color='green', s=10, label='Y', marker='s') # Y轴速度点plt.scatter(time_z, vel_z, color='blue', s=10, label='Z', marker='^') # Z轴速度点# 美化设置plt.xlabel('time (s)', fontsize=12)plt.ylabel('vel (m/s)', fontsize=12)plt.title('vel', fontsize=14)plt.grid(True, linestyle='--', alpha=0.5)plt.legend(loc='upper right', frameon=False)plt.tight_layout()# 绘制加速度图time_x, acc_x = self.merge_axis_data(Accx)time_y, acc_y = self.merge_axis_data(Accy)time_z, acc_z = self.merge_axis_data(Accz)plt.figure(figsize=(12, 6))plt.scatter(time_x, acc_x, color='#FF6347', s=10, label='X', marker='o') # 番茄红plt.scatter(time_y, acc_y, color='#20B2AA', s=10, label='Y', marker='o') # 浅海绿plt.scatter(time_z, acc_z, color='#6A5ACD', s=10, label='Z', marker='o') # 板岩蓝# 美化设置plt.xlabel('time (s)', fontsize=12)plt.ylabel('a (m/(s**2))', fontsize=12)plt.title('a', fontsize=14)plt.grid(True, linestyle='--', alpha=0.5)plt.legend(loc='upper right', frameon=False)plt.tight_layout()# 绘制加加速度图time_x, jerx = self.merge_axis_data(Jerx)time_y, jery = self.merge_axis_data(Jery)time_z, jerz = self.merge_axis_data(Jerz)plt.figure(figsize=(12, 6))plt.scatter(time_x, jerx, color='#FF6347', s=10, label='X', marker='o') # 番茄红plt.scatter(time_y, jery, color='#20B2AA', s=10, label='Y', marker='o') # 浅海绿plt.scatter(time_z, jerz, color='#6A5ACD', s=10, label='Z', marker='o') # 板岩蓝# 美化设置plt.xlabel('time (s)', fontsize=12)plt.ylabel('jerk (m/(s**3))', fontsize=12)plt.title('jerk', fontsize=14)plt.grid(True, linestyle='--', alpha=0.5)plt.legend(loc='upper right', frameon=False)plt.tight_layout()# 显示所有图像plt.show()# 返回优化路径return optimization_pathif __name__ == "__main__":# planner = TrajectoryPlanner()path = [[1, 1, 1], [2, 2, 1], [3, 3, 2], [4, 4, 3], [5, 5, 10]]initial_vel = [0.5, 0.5, 0.5]# 绘图并返回优化路径optimization_path = TrajectoryPlanner().plot_trajectory(path, initial_vel, plot_flag=False)print("Optimization Path:\n", optimization_path)相关文章:
)
无人机避障——如何利用MinumSnap进行对速度、加速度进行优化的轨迹生成(附C++python代码)
🔥轨迹规划领域的 “YYDS”——minimum snap!作为基于优化的二次规划经典,它是无人机、自动驾驶轨迹规划论文必引的 “开山之作”。从优化目标函数到变量曲线表达,各路大神疯狂 “魔改”,衍生出无数创新方案。 &#…...

2025 3D工业相机选型及推荐
3D工业相机是专门为工业应用设计的三维视觉采集设备,能够获取物体的三维空间信息,在智能制造、质量检测、机器人引导等领域有广泛应用。 一、主要类型 1.结构光3D相机 通过投射特定光斑或条纹图案并分析变形来重建三维形状 典型代表:双目结构…...
项目,后端接口报401-账号未登录解决方案)
芋道(yudao-cloud)项目,后端接口报401-账号未登录解决方案
一、需求 最近公司有新的业务需求,调研了一下,决定使用芋道(yudao-cloud)框架,于是从github(https://github.com/YunaiV/yudao-cloud)上克隆项目,选用的是jdk17版本的。根据项目启动手册&#…...

动态域名服务ddns怎么设置?如何使用路由器动态域名解析让外网访问内网?
设置路由器的动态域名解析(DDNS),通常需先选择支持 DDNS 的路由器和提供 DDNS 服务的平台,然后在路由器管理界面中找到 DDNS 相关设置选项,填入在服务平台注册的账号信息,完成配置后保存设置并等待生效。 …...

论文《Collaboration-Aware Graph Convolutional Network for Recommender Systems》阅读
论文《Collaboration-Aware Graph Convolutional Network for Recommender Systems》阅读 论文概况Introduction and MotivationMethodologyLightGCN 传播形式CIRCAGCNImplementation Experiments 论文概况 论文《Collaboration-Aware Graph Convolutional Network for Recomm…...

Codis集群搭建和集成使用的详细步骤示例
以下是Codis集群搭建和集成使用的详细步骤示例: 环境准备 安装Go语言环境 下载并安装适配操作系统的Go语言版本。配置环境变量GOROOT和GOPATH。 安装ZooKeeper 下载ZooKeeper压缩包,解压并进入目录。复制conf/zoo_sample.cfg为conf/zoo.cfg。启动ZooKe…...

利用比较预言机处理模糊的偏好数据
论文标题 ComPO:Preference Alignment via Comparison Oracles 论文地址 https://arxiv.org/pdf/2505.05465 模型地址 https://huggingface.co/ComparisonPO 作者背景 哥伦比亚大学,纽约大学,达摩院 动机 DPO算法直接利用标注好的数据来做偏好对…...

《数据库原理》部分习题解析
《数据库原理》部分习题解析 1. 课本pg196.第1题。 (1)函数依赖 若对关系模式 R(U) 的任何可能的关系 r,对于任意两个元组 t₁ 和 t₂,若 t₁[X] t₂[X],则必须有 t₁[Y] t₂[Y],则称属性集 Y 函数依赖…...

【HCIA】浮动路由
前言 我们通常会在出口路由器配置静态路由去规定流量进入互联网默认应该去往哪里。那么,如果有两个运营商的路由器都能为我们提供上网服务,我们应该如何配置默认路由呢?浮动路由又是怎么一回事呢? 文章目录 前言1. 网络拓扑图2. …...

基于机器学习的卫星钟差预测方法研究HPSO-BP
摘要 本文研究了三种机器学习方法(BP神经网络、随机森林和支持向量机)在卫星钟差预测中的应用。通过处理GPS和GRACE卫星的钟差数据,构建了时间序列预测模型,并比较了不同方法的预测性能。实验结果表明,优化后的BP神经…...

机器学习中分类模型的常用评价指标
评价指标是针对模型性能优劣的一个定量指标。 一种评价指标只能反映模型一部分性能,如果选择的评价指标不合理,那么可能会得出错误的结论,故而应该针对具体的数据、模型选取不同的的评价指标。 本文将详细介绍机器学习分类任务的常用评价指…...

AI 检测原创论文:技术迷思与教育本质的悖论思考
当高校将 AI 写作检测工具作为学术诚信的 "电子判官",一场由技术理性引发的教育异化正在悄然上演。GPT-4 检测工具将人类创作的论文误判为 AI 生成的概率高达 23%(斯坦福大学 2024 年研究数据),这种 "以 AI 制 AI&…...

langchain学习
无门槛免费申请OpenAI ChatGPT API搭建自己的ChatGPT聊天工具 https://nuowa.net/872 基本概念 LangChain 能解决大模型的两个痛点,包括模型接口复杂、输入长度受限离不开自己精心设计的模块。根据LangChain 的最新文档,目前在 LangChain 中一共有六大…...

蓝桥杯 10. 全球变暖
全球变暖 原题目链接 题目描述 你有一张某海域 N x N 像素的照片: . 表示海洋# 表示陆地 例如如下所示: ....... .##.... .##.... ....##. ..####. ...###. .......在照片中,“上下左右”四个方向上连在一起的一片陆地组成一座岛屿。例…...
OpenTiny icons——超轻量的CSS图标库,引领图标库新风向
我们非常高兴地宣布 opentiny/icons 正式发布啦! 源码:https://github.com/opentiny/icons(欢迎 Star ⭐) 官网:https://opentiny.github.io/icons/ 图标预览:https://opentiny.github.io/icons/brow…...

python使用OpenCV 库将视频拆解为帧并保存为图片
python使用OpenCV 库将视频拆解为帧并保存为图片 import cv2 import osdef video_to_frames(video_path, output_folder, frame_prefixframe_, interval1, target_sizeNone, grayscaleFalse):"""将视频拆分为帧并保存为图片参数:video_path (str): 视频文件路径…...

[论文阅读]ControlNET: A Firewall for RAG-based LLM System
ControlNET: A Firewall for RAG-based LLM System [2504.09593] ControlNET: A Firewall for RAG-based LLM System RAG存在数据泄露风险和数据投毒风险。相关研究探索了提示注入和投毒攻击,但是在控制出入查询流以减轻威胁方面存在不足 文章提出一种ai防火墙CO…...

机器学习 --- 数据集
机器学习 — 数据集 文章目录 机器学习 --- 数据集一,sklearn数据集介绍二,sklearn现实世界数据集介绍三,sklearn加载数据集3.1 加载鸢尾花数据集3.2 加载糖尿病数据集3.3 加载葡萄酒数据集 四,sklearn获取现实世界数据集五&#…...

在Ubuntu服务器上部署Label Studio
一、拉取镜像 docker pull heartexlabs/label-studio:latest 二、启动容器 (回到用户目录,例:输入pwd,显示 /home/<user>) docker run -d --name label-studio -it -p 8081:8080 -v $(pwd)/mydata:/label-st…...

机器学习07-归一化与标准化
归一化与标准化 一、基本概念 归一化(Normalization) 定义:将数据缩放到一个固定的区间,通常是[0,1]或[-1,1],以消除不同特征之间的量纲影响和数值范围差异。公式:对于数据 ( x ),归一化后的值…...

用vue和go实现登录加密
前端使用CryptoJS默认加密方法: var pass CryptoJS.AES.encrypt(formData.password, key.value).toString()使用 CryptoJS.AES.encrypt() 时不指定加密模式和参数时,CryptoJS 默认会执行以下操作 var encrypted CryptoJS.AES.encrypt("明文&quo…...

服务器制造业中,L2、L6、L10等表示什么意思
在服务器制造业中,L2、L6、L10等是用于描述服务器生产流程集成度的分级体系,从基础零件到完整机架系统共分为L1-L12共12个等级。不同等级对应不同的生产环节和交付形态,以下是核心级别的具体含义: L2(Level 2…...

mysql8常用sql语句
查询结果带行号 -- 表名为 mi_user, 假设包含列 id ,address SELECT ROW_NUMBER() OVER (ORDER BY id) AS row_num, t.id, t.address FROM mi_user t ; SELECT ROW_NUMBER() OVER ( ) AS row_num, t.id, t.address FROM mi_user t ; 更新某列数…...

多模态RAG与LlamaIndex——1.deepresearch调研
摘要 关键点: 多模态RAG技术通过结合文本、图像、表格和视频等多种数据类型,扩展了传统RAG(检索增强生成)的功能。LlamaIndex是一个开源框架,支持多模态RAG,提供处理文本和图像的模型、嵌入和索引功能。研…...

汽车工厂数字孪生实时监控技术从数据采集到三维驱动实现
在工业智能制造推动下,数字孪生技术正成为制造业数字化转型的核心驱动力。今天详细介绍数字孪生实时监控技术在汽车工厂中的应用,重点解析从数据采集到三维驱动实现的全流程技术架构,并展示其在提升生产效率、降低成本和优化决策方面的显著价…...

深度解码双重订阅用户:高价值流量池的掘金指南
在流量红利消退的当下,内容平台与电商平台的竞争已进入白热化阶段。数据显示,2023年全球用户平均每日切换应用频次超过200次,但仅有3%的用户愿意为多个平台持续付费。这3%的群体——“双重订阅用户”,正成为商业价值最高的流量金矿…...

MATLAB Simulink在Autosar和非Autosar工程下的开发流程
软件开发有两种方法:自上而下和自下而上。自上而下就是从整体出发去设计各个模块和模块间的接口,要求架构设计人员对产品功能非常清楚;自下而上就是从一个一个模块出发去设计,进而组成一个整体。自下而上可能会带来冗余代码过多和…...

使用DevEco Studio性能分析工具高效解决鸿蒙原生应用内存问题
目录 一、内存问题的识别与初步判断 1.1 内存问题的常见表现 1.2 使用 DevEco Profiler 的实时监控功能 1.2.1 打开 Profiler 工具 1.2.2 监控内存变化 1.2.3 判断内存异常 1.2.4 示例代码:模拟内存泄漏 二、内存问题的定界与定位 2.1 使用 Snapshot/Allocation 模板分…...

AI视频生成工具开发与搭建:从技术到应用的全方位指南
随着AI技术的飞速发展,视频创作的门槛被大幅降低。无论是个人用户还是企业开发者,都能通过AI工具实现照片转动态、视频爆改创意、小程序开发等多样化需求。本文将从技术开发、工具应用及行业趋势三个维度,深度解析AI视频生成的核心技术与实践…...

【android bluetooth 框架分析 02】【Module详解 7】【VendorSpecificEventManager 模块介绍】
1. 背景 我们在 gd_shim_module 介绍章节中,看到 我们将 VendorSpecificEventManager 模块加入到了 modules 中。 // system/main/shim/stack.cc modules.add<hci::VendorSpecificEventManager>();在 ModuleRegistry::Start 函数中我们对 加入的所有 module…...

Docker环境下的Apache NiFi安装实践踩坑记录
引言:由于最近用到数据同步,故打算采用中间件工具来做数据同步,谁知第一步部署Apache NiFi环境就耽搁了好久,其中遇到一些问题,故记录下来部署成功记录 问题1:HTTPS访问 HTTP ERROR 400 Invalid SNI问题2:…...

flutter Stream 有哪两种订阅模式。
Flutter 中的 Stream 有两种订阅模式: 单订阅模式 (Single Subscription) 只能有一个订阅者(listen 只能调用一次),后续调用会抛出异常。数据仅在订阅后开始传递,适用于点对点通信场景(如文件读取流…...

删除购物车中一个商品
一. 删除购物车中一个商品 删除商品时我们要考虑一个问题,当商品数量等于1时,删除商品就直接将其从数据库中删除即可。但是当数量大于1时,删除商品就是让商品数量-1。因此我们在删除一个商品时首先要判断该商品在购物车中的数量。 Controlle…...

EF Core 数据库迁移命令参考
在使用 Entity Framework Core 时,若你希望通过 Package Manager Console (PMC) 执行迁移相关命令,以下是常用的 EF Core 迁移命令: PMC 方式 ✅ 常用 EF Core PMC 命令(适用于迁移) 操作PMC 命令添加迁移Add-Migra…...

5月13日day24日打卡
元组和OS模块 知识点回顾: 元组可迭代对象os模块 作业:对自己电脑的不同文件夹利用今天学到的知识操作下,理解下os路径。 元组 元组的特点: 有序,可以重复,这一点和列表一样元组中的元素不能修改…...

[51单片机]---DS18B20 温度检测
1,DS18B20 2,DS18B20时序 void ds18b20_reset() {//ds18b20复位信号 拉低总线750us后释放总线DS18B20_PORT 0; delay_10us(75); DS18B20_PORT 1; delay_10us(2);}//为啥需要检测模块?当我们发生了复位,根据时序图,d…...

Win11 + Visual Studio 2022 + FLTK 1.4.3 + Gmsh 4.13.1 源码编译指南
一、编译环境准备 本文档详细记录了在 Windows 11 系统下,使用 Visual Studio 2022(版本 17)编译 FLTK 1.4.3 和 Gmsh 4.13.1 的完整过程。目标是帮助开发者顺利完成库的编译,并实现基本的功能测试。 二、编译 FLTK 1.4.3 2.1 …...

AUTOSAR图解==>AUTOSAR_TPS_ECUResourceTemplate
AUTOSAR ECU资源模板详解 基于AUTOSAR R4.4.0标准规范 目录 1. 简介 1.1 ECU资源模板的范围1.2 ECU资源模板概述 2. 一般硬件描述 2.1 硬件描述实体2.2 硬件类型2.3 硬件元素2.4 硬件引脚和引脚组2.5 硬件连接2.6 硬件类别定义 3. 硬件类型特定描述 3.1 硬件元素类别3.2 硬件引…...

如何在设计阶段考虑 Python 服务的可伸缩性,避免后期的重构
在如今的软件开发世界里,变化是唯一不变的主题。用户量可能一夜之间从几十人暴增到几十万,业务需求可能在半年内翻天覆地,技术栈也可能因为新工具的出现而需要调整。而作为开发者,尤其是用 Python 打造服务的开发者,我们常常会面临一个绕不过去的问题:如何让我们的服务在…...

ExoPlayer 如何实现音画同步
在解释这个问题之前,先讲一下 ExoPlayer 中音频播放的三种输出模式。 第一种是PCM模式(普通播放模式)。这是最基本的播放模式,音频以PCM(脉冲编码调制)数据形式处理,可以通过音频处理器进行各种…...

C++中void*知识详解和注意事项
一、void* 是什么? 在 C/C 中,void* 表示一个通用指针类型(generic pointer),可以指向任意类型的对象,但 不能直接解引用或进行算术运算,必须先进行类型转换。 void* ptr; // 可以指向任意类型…...

ssl 中 key 和pem 和crt是什么关系
.pem 文件(通用容器格式) 作用:PEM(Privacy-Enhanced Mail)是一种文本格式,可以存储 证书、私钥、中间证书 等。 特点: 以 -----BEGIN XXX----- 和 -----END XXX----- 包裹内容(如…...

CSS可以继承的样式汇总
CSS可以继承的样式汇总 在CSS中,以下是一些常见的可继承样式属性: 字体属性:包括 font-family (字体系列)、 font-size (字体大小)、 font-weight (字体粗细)、 font-sty…...

菜狗的脚步学习
文章目录 一、pdf到h文件转换并恢复二、三、 一、pdf到h文件转换并恢复 编写一个bat,将当前文件的.pdf文件后缀改为.h文件,然后将当前文件下的.h文件全部打开,再依次关闭,待所有.h文件都关闭后,再将.h文件改为.pdf后缀…...

latex公式格式
几个公式只标一个序号 \begin{equation}\begin{aligned}yX\\y2x\\y3x,\end{aligned} \end{equation}要想公式的等号对齐则用下面的格式 若想实现三个公式等号对齐且只编一个号,用 equation 包裹 aligned 环境即可 \begin{equation}\begin{aligned}y&X\\y&…...

在Babylon.js中实现完美截图:包含Canvas和HTML覆盖层
在现代Web 3D应用开发中,Babylon.js作为强大的3D引擎被广泛应用。一个常见的需求是实现场景截图功能,特别是当场景中包含HTML覆盖层(如UI控件、菜单等)时。本文将深入探讨如何在Babylon.js中实现完整的截图方案。 问题背景 这里我是希望实现一个渐隐的…...

LeetCode 648 单词替换题解
LeetCode 648 单词替换题解 题目描述 题目链接 在英语中,我们有一个叫做「词根」的概念,可以缩短其他单词的长度。给定一个词典和一句话,将句子中的所有单词用其最短匹配词根替换。 解题思路 哈希表 前缀匹配法 预处理词典:…...

从虚拟现实到混合现实:沉浸式体验的未来之路
摘要 近年来,虚拟现实(VR)和增强现实(AR)技术的快速发展,为沉浸式体验带来了前所未有的变革。随着技术的不断进步,混合现实(MR)作为VR和AR的融合形态,正在成为…...

基于深度学习的水果识别系统设计
一、选择YOLOv5s模型 YOLOv5:YOLOv5 是一个轻量级的目标检测模型,它在 YOLOv4 的基础上进行了进一步优化,使其在保持较高检测精度的同时,具有更快的推理速度。YOLOv5 的网络结构更加灵活,可以根据不同的需求选择不同大…...

黑马Java基础笔记-10
权限修饰符 修饰符同一个类中同一个包中其他类不同包的子类不同包无关类private√空着不写 (default)√√protected√√√public√√√√ 代码块 局部代码块(了解) public class Test {public static void main(String[] args) {{int a 10;System.out.println(a);}//运行到…...
