堆复习(C语言版)
目录
1.树的相关概念:
2.堆的实现
3.TopK问题
4.总结
1.树的相关概念:
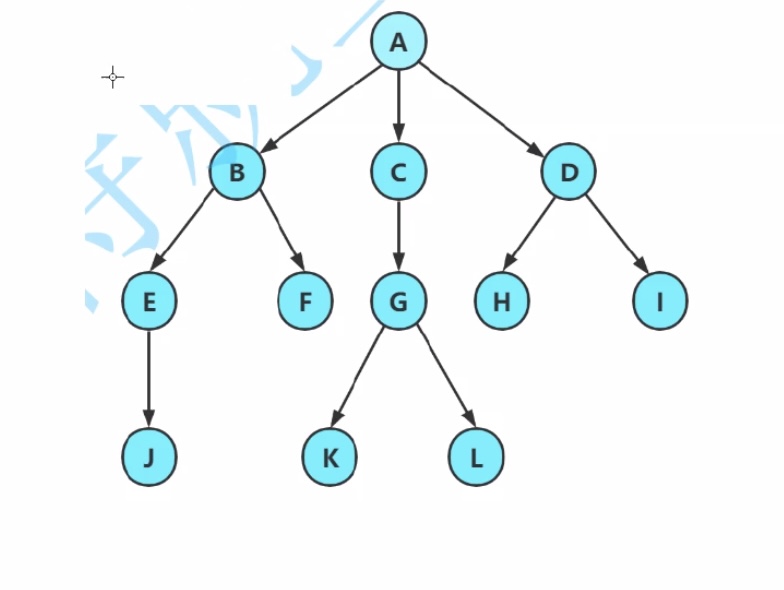
1.结点的度:一个结点含有的子树(孩子)个数。
A的度为6
2.叶结点or终端结点:度为0的结点。
J、K、L、H、I 都是叶子结点
3.非终端结点or分支结点:度不为0的结点
4.双亲结点or父结点:若一个结点含有子结点,那么这个结点被叫做该子结点的父结点。
5.孩子结点or子结点:和概念4反过来
A是B的父结点,B是A的子结点
6.兄弟结点:具有相同父结点的结点互称为兄弟结点
B、C、D是兄弟结点
7.堂兄弟结点:双亲在同一层的结点互为堂兄弟结点
E、F、G、H、I是堂兄弟结点
8.树的度:整棵树中最大的结点的度就是整棵树的度
树的度为3(即A的度,没有比A的度更大的)
9.树的层次:从根结点开始算,根为第1层(一般情况都是从第1层开始算,有些书本上也会从第0层开始算),其所有子节点为第2层,以此类推……
10.树的深度or高度:树中最大的层次
树的高度为4
11.结点的祖先:从根结点到该结点所经分支上的所有结点
L的祖先有G、C、A ,A是所有结点的祖先
12.子孙:和概念11反过来
L是G、C、A的子孙 ,所有结点都是A的子孙
13.森林:多棵互不相交的树组成的集合称为森林
14.一颗N个结点的树有N-1条边
15.对任何一棵二叉树,如果度为0的叶节点个数为m,度为2的分支结点个数为n,则有m = n+1
树的构建是用递归来实现的,把一整棵树看成一个根节点+几个子树,把子树看作一个子树的根节点+子树的子树,以此类推……,直到叶子结点
逻辑结构:想象出来的,例如二叉树就是典型的逻辑结构
物理结构(存储结构):实际编程时所使用的结构,数组、链表这些就是物理结构
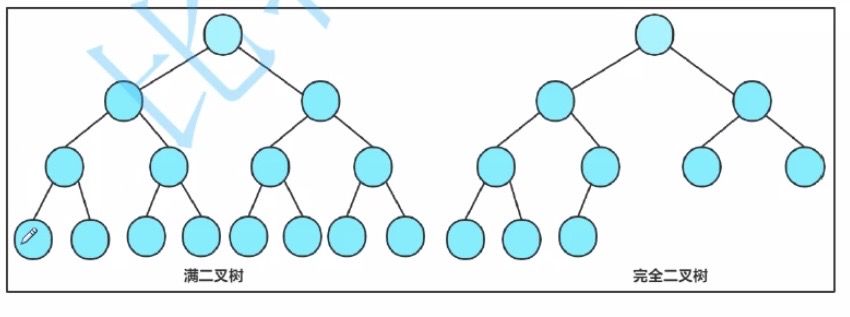
特殊的二叉树:
1.满二叉树:每一层都是满的二叉树
假设满二叉树树有N层
第一层 -> 2^0 个结点
第二层 -> 2^1 个结点
……
第N层 -> 2^(N-1)个结点
sum(1+2+……+N) = 2^0 + 2^1 + …… + 2^(N-1) = 2^N - 1 (等比数列求和)
假设满二叉树共有H个结点
2^N - 1 = H ,N = log2(H+1)
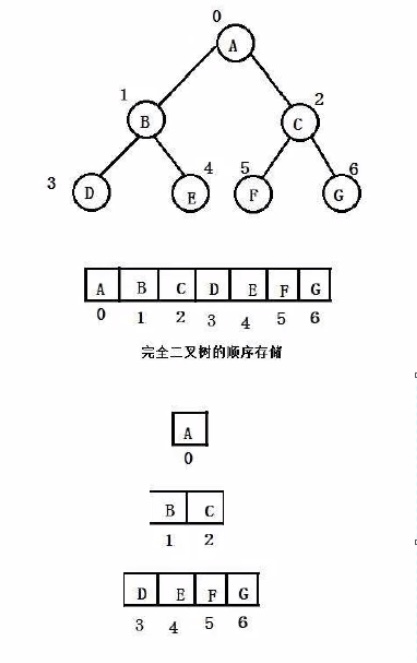
2.完全二叉树:前 N - 1 层都是满的,最后一层不满且从左到右必须是连续的
当我们用数组实现完全二叉树时(只有完全二叉树、满二叉树可以用数组实现,否则数组中有些下标对应的元素为空,会存在大量的空间浪费)
假设父亲在数组中的下标:i
左孩子在数组中的下标:2*i + 1
右孩子在数组中的下标:2*i + 2
假设孩子在数组中的下标:j
父亲在数组中的下标:( j-1 ) / 2
因为 "(4-1) / 2 = (4-2) / 2 ",所以不用区分是左孩子还是右孩子
2.堆的实现
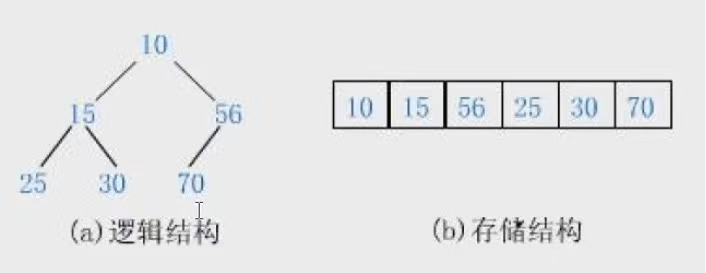
堆是一个完全二叉树,堆分为了大根堆(任何一个父亲≥孩子)、小根堆(任何一个父亲≤孩子)
上图所示的即为小根堆
题1:
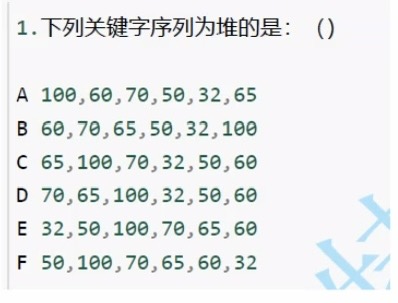
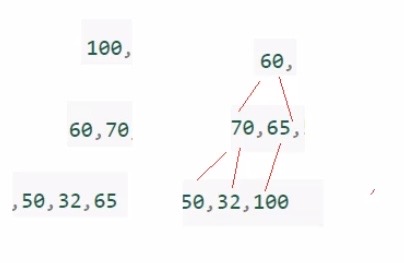
该类题目先是按照完全二叉树的概念,拆分成h层,然后看上下两层的元素是否都满足同一种大小关系
A选项中,即使60<65,但是70大于65,依旧满足大根堆的概念
B选项中,100大于上一层中的任何一个元素,所以不是堆
……
答案为A
void Adjustup(int* a, int child) //此处的child和parents都是表示数组的下标
{//初始化双亲结点int parents = (child - 1) / 2;while (child > 0){if (a[child] < a[parents])//小根堆{Swap(&a[child], &a[parents]);//改变两个元素的位置child = parents;parents = (child - 1) / 2;}else break;}
}void AdjustDown(int* a,int n, int parent)
{//先假设左孩子小int child = parent * 2 + 1;//如果child >= size(n),说明已经到了叶子节点,停止循环while (child < n){//找出小的那个孩子(先得判断有没有右孩子,这也就是假设左孩子小,不假设右孩子小的原因)if (child + 1 < n && a[child + 1] < a[child])child++;//右孩子比较小,改为右孩子//交换or不交换位置,父节点小于小的子节点时,说明找到了该在的位置if (a[parent] <= a[child]) break;else{Swap(&a[parent],&a[child]);parent = child;child = parent * 2 + 1;}}
}

向上调整、向下调整算法是实现堆还有堆排序最重要的一个算法
AdjustUp函数(上图1):
每次有新的元素插入到二叉树(也可以看作是数组)以后,每次都进行结点和父节点的比较,直到该结点比父节点小时停止位置交换(上图是push函数的流程图,push函数用到的就是向下调整)
AdjustDown函数(上图2):
比较父结点的2个子节点的大小,和小的那个子节点交换位置,这样最后放在上一层的结点要比原兄弟结点和原父节点的元素都小,同时可以保证根节点永远是整个数组中最小的(上图是pop函数的流程图,pop函数用到的就是向下调整)
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef struct heap
{int* a;int size;int capacity; // 当结点数量很多时,可能需要扩容
}hp;void Adjustup(int* a, int child);
void AdjustDown(int* a, int n, int parent);
void HPInit(hp* php);
void HPDestroy(hp* php);
void HPPush(hp* php, int x);
void HPPop(hp* php);
int HPTop(hp* php);
bool HPEmpty(hp* php);
void HPDestory(hp* php);
//heap.h#include"heap.h"void HPInit(hp* php)
{assert(php);php->a = NULL;php->capacity = php->size = 0;
}
void HPDestroy(hp* php)
{assert(php);free(php->a);php->a = NULL;php->capacity = php->size = 0;
}
void Swap(int* a, int* b)
{int c = *a;*a = *b;//把a地址处的元素变为b位置处的元素*b = c;
}
void Adjustup(int* a, int child) //此处的child和parents都是表示数组的下标
{//初始化双亲结点int parents = (child - 1) / 2;while (child > 0){if (a[child] < a[parents])//小根堆{Swap(&a[child], &a[parents]);//改变两个元素的位置child = parents;parents = (child - 1) / 2;}else break;}
}
void HPPush(hp* php, int x)
{ //扩容or初始化if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;int* temp = (int*)realloc(php->a, sizeof(int) * newcapacity);if (!temp){perror("realloc failure");return;}php->a = temp;php->capacity = newcapacity;}//开始插入php->a[php->size++] = x;//开始向上调整Adjustup(php->a, php->size-1);
}
void AdjustDown(int* a,int n, int parent)
{//先假设左孩子小int child = parent * 2 + 1;//如果child >= size(n),说明已经到了叶子节点,停止循环while (child < n){//找出小的那个孩子(先得判断有没有右孩子,这也就是假设左孩子小,不假设右孩子小的原因)if (child + 1 < n && a[child + 1] < a[child])child++;//右孩子比较小,改为右孩子//交换or不交换位置,父节点小于小的子节点时,说明找到了该在的位置if (a[parent] <= a[child]) break;else{Swap(&a[parent],&a[child]);parent = child;child = parent * 2 + 1;}}
}void HPPop(hp* php)
{assert(php);assert(php->a > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}bool HPEmpty(hp* php)
{assert(php);return php->size == 0;
}int HPTop(hp* php)
{assert(php);assert(php->size > 0);return php->a[0];
}void HPDestory(hp* php)
{assert(php);free(php->a);php->a = NULL;php->capacity = php->size = 0;
}
//heap.c#include"heap.h"void Test1()
{//根据堆的特性,每次输出根节点以后,把根节点删除后重复刚才的操作,那么输出的结果就是有序的int a[] = { 4,2,9,7,5,6,8,3,1 };hp HP;HPInit(&HP);for (size_t i = 0; i < sizeof(a) / sizeof(int); i++){HPPush(&HP,a[i]);}int i = 0;while (!HPEmpty(&HP)) //非空就不断执行{printf("%d ", HPTop(&HP));HPPop(&HP);}HPDestory(&HP);printf("\n");
}void HPSort(int* a,int n)
{//for (int i = 1; i < n; i++)//Adjustup(a, i); //向上调整建立小堆操作,时间复杂度为nlognfor (int i = (n - 1 - 1) / 2; i >= 0; i--)AdjustDown(a, n, i);//从最后一个父节点开始,依次向下调整,直到调整到根节点为止,时间复杂度为nint end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0); end--;}
}void Test2()
{int a[] = { 4,2,9,7,5,6,8,3,1 };HPSort(a, sizeof(a) / sizeof(int));for (int i = 0; i <= 8; i++) printf("%d ", a[i]);printf("\n");
}int main()
{Test1();Test2();return 0;
}
//test.C代码重点讲解:
HPPush函数:
在物理结构中,插入操作是插入在数组的后面
假设是小根堆,元素x插入j下标位置时,如果(j-1)/2下标位置处的元素y小于x,那么直接插入;否则就先插入,然后两者互换位置,再对互换完位置的x与上面的父结点y相比较,重复刚才的操作
最坏情况可能要和根节点交换位置
HPPop函数:
不能直接数组所有元素向前1位,如此操作兄弟结点可能变为了父节点,堆关系大概率就不存在了
因此可以把要删除的元素和最后一个元素进行交换,删除数组最后一个元素对整个堆不会有任何影响
然后把换了位置后的元素进行向下调整(向上调整的逆操作),向下调整是因为他原本所在最后一层,会是一个比较大or比较小元素(大小根堆的不同)用作删除堆顶的数据(即根节点的数据),每次删除的元素都是最大or最小的元素(堆的特性)
下图1为流程图
HPSort函数:
把数组直接看成一棵二叉树,然后把二叉树中所有元素(除根节点外)进行一次向上调整,每个元素就能找到他们应该存在的位置,这样就能直接把无序数组搞成一个堆了(代码如下图2);但由于这样操作,从根节点到叶子节点的所有数据都要向上调整一次,而叶子节点的向上调整次数最多可以占到所有向上调整次数的半数以上,所以我们此处进行了一定的优化(优化成向下调整)
创建小堆:如果要把数组中的元素进行降序排序,先建立一个小堆,然后进行类似于HPPop的操作(第一个元素和最后一个元素交换位置,然后把当前第一个元素向下调整,如此就能第一个元素(根节点元素)永远是最小的),这样即可完成操作;从最后一个父节点开始,依次向下调整,直到调整到根节点为止,因为叶子节点向下调整也没有东西可以调了,并且最后一层叶子节点(如果是满二叉树),那么叶子结点的函数调用次数将占到所有调用次数的50%,因此从最后一个父节点开始遍历是很大的优化
排序:排完小根堆以后,根节点就是最小值了,此时将根节点与末尾元素交换,每次再对交换上来的末尾元素向下调整(保持小堆特性),就能保住根节点永远是最小的,这样放到末尾的肯定也是最小的;将一个最小的元素放在了末尾以后,下标需要不断往前推移(因为当某个元素放在末尾以后,位置就不需要再进行改动了),直到下标为0时(下标为0时,所有元素都已经排序完毕了,不需要再对已经排完序的数组进行一次操作了),时间复杂度为nlogn
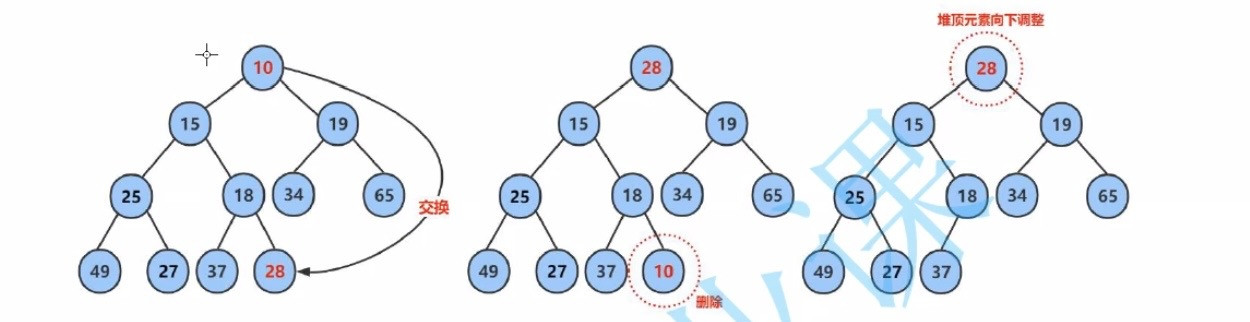
注:若使用大根堆,则此时最头部的元素为最大值;那假设我们把最大值放在最后,然后把所有数据往前移动1位(数组视角),覆盖掉前面数据,再对最头部的元素进行向下调整(保持大根堆特性),这是否可行?
答:这是不可行的,因为数组是被看作完全二叉树的,往前覆盖时结点与结点之间的关系发生了改变(兄弟节点变成了子节点,父结点变成了祖先结点)(如下图3)
代码实现的是降序排序,如果要把降序改为升序就把AdjustDown中的 “a[child + 1] < a[child]” 和 “a[parent] <= a[child]”改为 “a[child + 1] > a[child]” 和 “a[parent] >= a[child]”记忆方法:降序小堆、升序大堆(降小升大)


插入删除结点时,向上向下调整算法的时间复杂度为什么是O(logN)?
如上图所示,完全二叉树的层数近似于log2(N),因此无论是向上还是向下调整的次数都为log2(N)次,所以时间复杂度为O(logN)
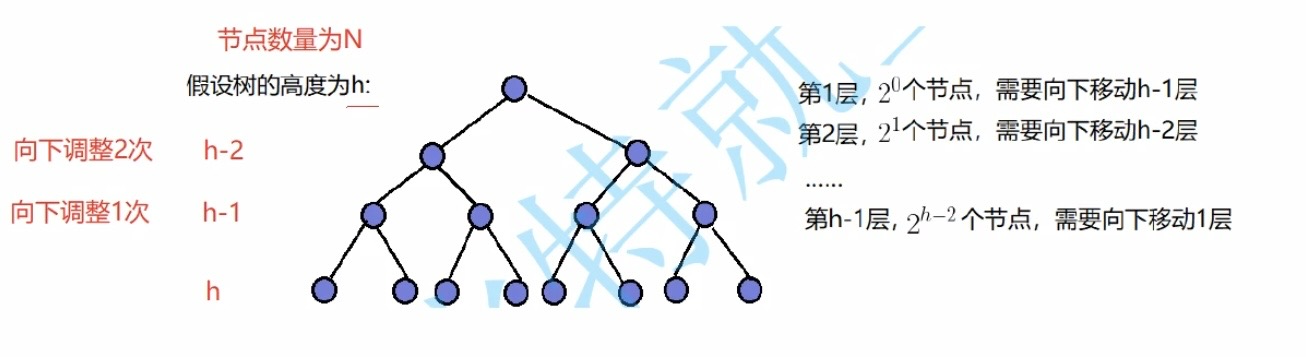
使用向下调整算法完成建堆操作时,为什么时间复杂度为O(N)?
如下图所示(向下调整指的是最大向下调整次数),根据数学归纳法不难得出
T(h) = 2^0 * (h-1) + 2^1 * (h-2) + …… + 2^(h-3) * 2 + 2^(h-2) * 1
T(h)计算向下调整建堆最坏情况下合计的调整次数
从后往前看,第h-1层有2^(h-2)个结点,最多向下调整1次……(以此类推,得出该式)
对该式进行错位相减法,具体操作如下所示:
2 * T(h) = 2^1 * (h-1) + 2^2 * (h-2) + …… + 2^(h-2) * 2 + 2^(h-1) * 1 = D(h)
D(h) - T(h) = 2^1 + 2^2 + …… + 2^(h-2) + 2^(h-1) * 1 - 2^0*(h-1) = T(h)
错位相减法使用说明:以 2^1*(h-1) 和 2^1*(h-2) 为例,最后结果为 2^1 ;因为两式的 2^(x) 系数不同但系数的差值恒为1,所以后续都只保留 2^(x) 部分 ;然后再把剩下的没有对应式子的抄下来即可
- 2^0*(h-1) = 2^0 - 2^0*h
2^(h-1) * 1 = 2^(h-1)
F(h) = 2^h - 1 = N (高度为h的满二叉树的结点个数)
T(h) = 2^h - 1 - h = N - h -> 时间复杂度为O(N)
为什么向上调整算法实现建堆时间复杂度远高于向下调整算法?
向上调整:结点数量多的层 * 调整次数多(最后一层需要最多次调整)
结点数量少的层 * 调整次数少
向下调整:结点数量多的层 * 调整次数少(最后一层不需要调整)
结点数量少的层 * 调整次数多
3.TopK问题

方法1:
建立一个N个数的大堆 O(N)
top pop k次 O(k*logN) = O(logN)
如果有10亿个整数数据(40亿字节)建堆,那么需要多少内存空间?
4GB = 4*1024MB = 4*1024*1024KB = 4*1024*1024*1024Byte > 40亿Byte ,因此需要用不到4G的内存去存储10亿个整型数据,内存条倍感压力……
假设只有1G内存,那么可以每次只对1G的数据内容找最大的k个,进行了 x(x = sumGB/1GB)该操作后,在找到的 x*k 个数据中再去找最大的k个
但假设只有1M甚至1K内存,那么这样的操作时间复杂度就过高了
由于不是内存空间占用过大,就是时间复杂度过高,因此该方法并不优秀
方法2:
用数据中的前k个数,建一个小堆;剩下的N-k个数依次与栈顶数据进行比较,如果比栈顶的数据大,就代替栈顶进堆(覆盖根位置,然后向下调整);遍历完以后小堆里的k个数,就是最大的k个数
k个数的完全二叉树创建,时间复杂度为logk;对剩余数据进行遍历,时间复杂度为N-k
总的时间复杂度:logk * (N-k) = O(N)
#include"heap.h"void TopK(int k) //解决topK问题,即从N个数中找最大的前k个(类似于现实中的游戏排行榜)
{int a[] = { 4,2,9,7,5,6,8,3,1 };//创建k个数据的小堆for (int i = (k - 1 - 1) / 2; i >= 0; i--)AdjustDown(a, k, i);int i = k;//对剩下的N-k个数据进行遍历while (i < sizeof(a) / sizeof(int)){if (a[0] < a[i]){//覆盖数据a[0] = a[i];//在小堆中向下调整AdjustDown(a, k, 0);i++;}else //比最小的小,直接跳过不用放入堆中{i++;continue;}}for (int i = 0; i <= k - 1; i++)printf("%d ", a[i]);
}int main()
{TopK(3);return 0;
}
//test.c代码重点讲解:
创建小堆时,直接在数组中进行创建;堆有k个元素,映射到数组下标就是k-1;把[0,k-1]下标的数组看作完全二叉树,创建时直接从最后的父节点开始依次向下调整,最后的父节点根据完全二叉树子节点与父节点关系公式: (j-1)/2 = i ,可以得出下标为 (k - 1 - 1)/2
然后再对原数组[k,n-1]下标的元素进行遍历,其余操作如上文所述
4.总结
1.堆---数据结构---C++stl库中的priority_queue
2.堆排序
3.topK问题
4.堆排序、topK的时间复杂度问题
相关文章:
)
堆复习(C语言版)
目录 1.树的相关概念: 2.堆的实现 3.TopK问题 4.总结 1.树的相关概念: 1.结点的度:一个结点含有的子树(孩子)个数。 A的度为6 2.叶结点or终端结点:度为0的结点。 J、K、L、H、I 都是叶子结点 3.非终端结…...

解决LangChain4j报错HTTP/1.1 header parser received no bytes
问题描述 当使用langchain4j-open-ai调用自己部署的大模型服务时报错: public static void main(String[] args) {OpenAiChatModel model OpenAiChatModel.builder().apiKey("none").modelName("qwen2.5-instruct").baseUrl("http://19…...
:案例与实战技巧)
深入解析MySQL联合查询(UNION):案例与实战技巧
在数据库操作中,查询是最常用的操作之一。MySQL提供了强大的查询功能,联合查询(UNION)是其中非常有用的一项操作。联合查询可以将多个查询结果合并成一个结果集,使得从不同来源的数据整合变得更加简单高效。本文将详细…...

[计算机科学#14]:数据结构
【核知坊】:释放青春想象,码动全新视野。 我们希望使用精简的信息传达知识的骨架,启发创造者开启创造之路!!! 内容摘要:数据结构是计算机科学中的核心概念,用于…...

【计算机网络】HTTP 协议
HTTP是什么? HTTP 全称是“超文本传输协议”,是互联网上应用最广泛的应用层协议,用于客户端和服务器之间的通信。 HTTP 的实现在 HTTP 3.0之前都是基于传输层的 TCP 实现的, HTTP 3.0 改为了基于 UDP 实现,但是现在市…...

原生的 XMLHttpRequest 和基于 jQuery 的 $.ajax 方法的异同之处以及使用场景
近期参与一个项目的开发,发现项目中的ajax请求有两种不同的写法,查询了下两种写法的异同之处以及使用场景。 下面将从以下两段简单代码进行异同之处的分析及使用场景的介绍: // 写法一: var xhr new XMLHttpRequest(); xhr.open…...
)
横向移动(上)
横向移动(上) 横向移动指的是攻击者在内网中获得初始访问权限之后,通过相关技术扩大敏感数据和高价值资产权限的行为 常见的横向移动的方式 1.通过web漏洞 2.通过远程桌面 3.通过账号密码 4.通过不安全的配置 5.通过系统漏洞 利用远控…...

关于 js:7. 模块化、构建与工具链
一、模块系统:CommonJS、ESM、UMD 模块系统的目标: 将代码拆分为独立的逻辑单元(模块),实现封装、复用、依赖管理。 在 Web 前端/Node 中,因为 JavaScript 起初没有模块机制,因此出现了多个模…...
)
一次IPA被破解后的教训(附Ipa Guard等混淆工具实测)
一行代码的疏忽,一个默认的类名,一个未混淆的资源路径,都可能成为攻击者入侵的入口。 背景:一次“不值一提”的上线,成了代价惨重的经验 故事的起点很简单:我们给销售部门做了一款小型内部演示 App&#x…...

麒麟系统安装.net core环境变量
本文主要记录在麒麟系统上安装.net core的运行环境,这里使用的是麒麟V10桌面版,后续测试服务器到了之后再使用服务器版进行安装测试。 环境安装 下载 这里由于是桌面版,我直接使用浏览器下的包,下完之后在终端中安装。 安装 1…...

如何使用 React Hooks 替代类组件的生命周期方法?
文章目录 1. 引言2. useEffect 概述3. 模拟类组件的生命周期方法3.1 模拟 componentDidMount3.2 模拟 componentDidUpdate3.3 模拟 componentWillUnmount 4. 多个 useEffect 的使用5. 注意事项6. 总结 1. 引言 在 React 16.8 版本之前,开发者主要通过类组件&#x…...

windows 在安装 Ubuntu-20.04 显示操作超时解决办法
1. 问题概述与原因分析 在我们用下面命令安装 Ubuntu-20.04 时系统显示操作超时: wsl --install -d Ubuntu-20.04大概率是没打开 Windows 虚拟机监控程序平台,可以在控制面板–>程序和功能里面打开 2. 解决办法与步骤 解决方式如下: 我…...

Spring Boot中Redis序列化配置详解
精心整理了最新的面试资料和简历模板,有需要的可以自行获取 点击前往百度网盘获取 点击前往夸克网盘获取 引言 在使用Spring Boot集成Redis时,序列化方式的选择直接影响数据存储的效率和系统兼容性。默认的JDK序列化存在可读性差、存储空间大等问题&am…...

OpenCV进阶操作:光流估计
文章目录 前言一、光流估计1、光流估计是什么?2、光流估计的前提?1)亮度恒定2)小运动3)空间一致 3、OpenCV中的经典光流算法1)Lucas-Kanade方法(稀疏光流)2) Farneback方…...
)
2025年渗透测试面试题总结-渗透测试红队面试八(题目+回答)
网络安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 渗透测试红队面试八 二百一十一、常见中间件解析漏洞利用方式 二百一十二、MySQL用户密码存储与加密 …...

前端面试高频50个问题,解答
以下是前端面试中常见的50个高频问题及其简要解答: HTML HTML5 有哪些新特性? 语义化标签(如 <header>、<footer>)、多媒体支持(如 <audio>、<video>)、本地存储(如 l…...

Elasticsearch架构原理
1、Elasticsearch的节点类型 1.1 Master节点 在Elasticsearch启动时,会选举出来一个Master节点。当某个节点启动后,然后 使用Zen Discovery机制找到集群中的其他节点,并建立连接。 discovery.seed_hosts: ["192.168.21.130", &qu…...

前端面试宝典---webpack面试题
webpack 的 tree shaking 的原理 Webpack 的 Tree Shaking 过程主要包含以下步骤: 模块依赖分析:Webpack 首先构建一个完整的模块依赖图,确定每个模块之间的依赖关系。导出值分析:通过分析模块之间的 import 和 exportÿ…...

Vue 2 项目中配置 Tailwind CSS 和 Font Awesome 的最佳实践
Vue 2 项目中配置 Tailwind CSS 和 Font Awesome 的最佳实践 一、Tailwind CSS 配置 1. 安装依赖 npm install tailwindcssnpm:tailwindcss/postcss7-compat tailwindcss/postcss7-compat postcss^7 autoprefixer^92. 创建配置文件 npx tailwindcss init3. 创建样式文件 在…...

hiveserver2与beeline进行远程连接hive配置及遇到的问题
1、hiveserver2 参与用户模拟功能,因为开启后才能保证各用户之间的权限隔离。 1.1、配置 $HADOOP_HOME/etc/hadoop/core-site.xml <!--配置所有节点的root用户都可作为代理用户--> <property><name>hadoop.proxyuser.root.hosts</name>&…...

单词短语0512
当然可以,下面是“opportunity”在考研英语中的常用意思和高频短语,采用大字体展示,便于记忆: ✅ opportunity 的考研常用意思: 👉 机会,良机 表示有利的时机或条件,尤指成功的可能…...
)
c++刷题便捷函数(类似于stoi的小函数)
标题 stoi(字符串转整形)map和set都有count成员函数,返回值是该key的个数,可以用来查是否存在该元素。bool is_sorted(nums.begin(), nums.end() 检验是否有序INT_MAX,INT_MIN分别是整形最大和最小初始化二维矩阵 vector<vector\<int>> mart…...

想实现一个基于MCP的pptx生成系统架构图【初版实现】
技术栈:Python + MCP协议 + python-pptx + FastMCP 核心创新点:通过MCP协议实现PPTX元素的动态化生成与标准化模板管理 当前还是个半成品,后续持续更新。 主要先介绍一下思路。 一、MCP协议与系统设计原理 1.1 为什么选择MCP? 标准化工具调用:通过MCP将PPTX元素生成逻辑封…...

jwt学习
基于token的鉴权机制也是无状态的(类似于http协议),不需要保在服务端保留用户的认证或会话信息。 构成 jwt由三部分构成:头部、payload、签名,中间用.隔开 头部(header) 包含两部分信息:声明类型、声明加密的算法 例如:…...

pth的模型格式怎么变成SafeTensors了?
文章目录 背景传统模型格式的安全隐患效率与资源瓶颈跨框架兼容性限制Hugging Face 的解决方案:SafeTensors行业与社区的推动SafeTensors 的意义总结 背景 最近要找一些适合embedding的模型,在huggingface模型库上看到一些排名比较靠前的,准…...

如何判断IP是否被平台标记
一、基础检测:连通性与黑名单筛查 网络连通性测试 Ping与Traceroute:通过命令测试延迟和路由路径,若延迟>50ms或存在异常节点(如某跳延迟>200ms),可能影响可用性。示例命令: bash ping 8.…...

【c++】异常详解
目录 C语言处理错误的局限性异常的定义异常的具体使用细则异常的抛出与捕获在函数调用链中异常栈展开匹配原则异常的重新抛出异常规范throw(类型)noexcept 成熟的异常体系c自己的异常体系异常的优缺点优点缺点 异常安全 C语言处理错误的局限性 C语言处理错误常常会用到assert和…...

从模型加密到授权交付,CodeMeter赋能3D打印商业化全流程
引言 在数字化制造快速演进的当下,3D 打印(增材制造)作为具备高度灵活性与创新潜力的制造方式,正重塑备件供应链与产品生命周期管理。然而,随着应用场景不断扩展,企业面临的知识产权保护、数字资产商业化与…...

ESP32开发之freeRTOS的事件组
什么是事件组事件组的应用场景事件组的API函数事件组应用举例总结什么是事件组 概念:事件组就是一个整数,高8位给内核使用,其他位用来表示事件。在ESP32的IDF freeRTOS中,这个整数是32位的,低24位用来供事件组使用。 举一个生活中的例子: 你在等快递,有三个包裹来自不…...

K8S中构建双架构镜像-从零到成功
背景介绍 公司一个客户的项目使用的全信创的环境,服务器采用arm64的机器,而我们的应用全部是amd64的,于是需要对现在公司流水线进行arm64版本的同步镜像生成。本文介绍从最开始到最终生成双架构的全部过程,以及其中使用的相关配置…...

腾讯怎样基于DeepSeek搭建企业应用?怎样私有化部署满血版DS?直播:腾讯云X DeepSeek!
2025新春,DeepSeek横空出世,震撼全球! 通过算法优化,DeepSeek将训练与推理成本降低至国际同类模型的1/10,极大的降低了AI应用开发的门槛。 可以预见,2025年,是AI应用落地爆发之年! ✔…...

【论信息系统项目的质量管理】
论信息系统项目的质量管理 前言一、抓好质量管理规划工作,为质量管理和确认提供指南和方向。二、做好管理质量相关工作,促进质量过程改进。三、抓好控制质量,确保实现质量目标四、综合协调质量与成本、进度、范围的关系总结 前言 为解决日常出…...

SpringAI框架中的RAG模块详解及应用示例
SpringAI框架中的RAG模块详解及应用示例 RAG(Retrieval-Augmented Generation)可以通过检索知识库,克服大模型训练完成后参数冻结的局限性,携带知识让大模型根据知识进行回答。SpringAI框架提供了模块化的API来支持RAG࿰…...

图像增强技术
一、目的 通过本实验加深对数字图像增强操作的理解,熟悉MATLAB中的有关函数;了解直方图均衡化和卷积滤波的原理;熟悉低通和高通滤波模板的构造方法。 二、实验内容与设计思想 1、观察实验结果可看出, 原图像 I的对比度较低&…...

【Java学习笔记】多态参数
多态参数 应用:方法定义的形参类型为父类类型,实参允许为子类类型 // 父类 package polyparemeter;public class employee {private String name;private double salary;//构造器public employee(){}public employee(String name, double salary) {thi…...

计算机网络核心技术解析:从基础架构到应用实践
计算机网络作为现代信息社会的基石,承载着全球数据交换与资源共享的核心功能。本文将从网络基础架构、核心协议、分层模型到实际应用场景,全面解析计算机网络的核心技术,并结合行业最新趋势,为读者构建系统的知识体系。 一、计算机…...

LiveData:Android响应式编程的核心利器
LiveData是一种可观察的数据持有类,用于在Android应用中实现数据的响应式编程。它具有以下特点和作用: 特点 生命周期感知:LiveData能够感知与其关联的组件(如Activity、Fragment)的生命周期状态。只有当组件处于活跃状态(如Activity处于RESUMED状态)时,LiveData才会将…...

【LeeCode】1.两数之和
文章目录 1. 暴力求解2. 哈希表具体过程1. nums [2, 7, 11, 15],target 9:2. nums [11, 15, 2, 7], target 9 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数ÿ…...

继承关系下创建对象的具体流程
public class Person {int x initX(); // 显式初始化:调用方法 initX()public Person() {System.out.println("Parent 构造器执行, x " x);}int initX() {System.out.println("initX() 被调用了");return 100;} }public class Child extends…...
的中国土壤数据集(v1.1)(2009))
基于世界土壤数据库(HWSD)的中国土壤数据集(v1.1)(2009)
时间分辨率:年共享方式:开放获取数据大小:156.47 MB数据时间范围:2009元数据更新时间:2020-03-26 数据集摘要 数据来源于联合国粮农组织(FAO)和维也纳国际应用系统研究所(IIASA)所构建的世界土…...

mac M2能安装的虚拟机和linux系统系统
目前网上的资料大多错误,能支持M2的很少。 推荐安装的改造过的centos7也无法进行yum操作,建议安装centos8 VMware Fusion下载地址: https://pan.baidu.com/s/14v3Dy83nuLr2xOy_qf0Jvw 提取码: jri4 centos8下载地址: https://…...
 】)
212. 单词搜索 II【 力扣(LeetCode) 】
文章目录 零、原题链接一、题目描述二、测试用例三、解题思路四、参考代码 零、原题链接 212. 单词搜索 II 一、题目描述 给定一个 m x n 二维字符网格 board 和一个单词(字符串)列表 words, 返回所有二维网格上的单词 。 单词必须按照字母…...

【软考-高级】【信息系统项目管理师】论文写作注意事项及2014年至2024年历年论文题目汇总
论文写作注意事项 要求 字数要求:2500字以内(2024年超过2500字,在线答题系统无法输入)时长要求:2小时(大多数人不够用)内容要求: 必须响应子标题,如子标题要求写如何优…...

MySQL数据库表的约束
目录 1.null属性 2.默认值约束(default) 3.comment 4.zerofill 5.主键(primary key) 6.自增长(auto_increment) 7.唯一键(unique) 编辑 8.外键 约束是为了安全插入数据&a…...

硅基计划2.0 学习总结 壹 Java初阶
一、初见Java (1)Java简介 首先不得不承认Java是一门优秀的程序设计语言 其系列的计算机软件和跨平台体系包括国内的生态链完善是C/C语言难以弥补的 (2)Java SE 全称Java Standard Edition,是Java体系的基础 &am…...

逆向破解:x64dbg
文章目录 一、CPU窗口1、反汇编窗口2、寄存器窗口3、栈地址窗口4、十六进制数据窗口5、堆栈参数解析窗口 二、常用快捷键三、字符串检索功能四、调试功能1、上一步 一、CPU窗口 1、反汇编窗口 2、寄存器窗口 寄存器窗口用于显示和解释当前线程环境下CPU寄存器的各种状态值和内…...

从MCU到SoC的开发思维转变
目录 1、硬件设计 2、软件开发 3、调试与测试 4、电源管理 微控制器单元(MCU)和系统级芯片(SoC)是嵌入式开发中最常见的两种处理器类型。MCU以其简单、低功耗的特点,广泛应用于特定控制任务;而SoC凭借强…...

3DGS-to-PC:3DGS模型一键丝滑转 点云 or Mesh 【Ubuntu 20.04】【2025最新版!!】
一、引言 3D高斯泼溅(3DGS)是一种新兴的三维场景表示方法,可以生成高质量的场景重建结果。然而,要查看这些重建场景,需要特殊的高斯渲染器。大多数3D处理软件并不兼容3D高斯分布模型,但它们通常都兼容点云文件。 3DGS-to-PC项目提…...

互联网大厂Java求职面试:优惠券服务架构设计与AI增强实践-3
互联网大厂Java求职面试:优惠券服务架构设计与AI增强实践-3 场景背景 面试场景设定在一家大型互联网公司,面试官为拥有10年以上经验的技术总监,专注于高并发、高可用系统的架构设计。候选人郑薪苦是一名技术潜力十足的程序员,擅…...

ABP-Book Store Application中文讲解 - 前期准备 - Part 3:Acme.BookStore项目模块详解
ABP-Book Store Application中文讲解-汇总-CSDN博客 本文通过对Acme.BookStore项目各模块的详解,让大家知道每个project用来干什么的,他们之间的引用关系是什么,同时知道怎样添加新的功能模块。 Acme.Bookstore 是主要 ABP Studio 模块的主…...
