当前位置：首页 > news >正文

【递归、搜索和回溯】二叉树中的深搜

news 来源：原创 2025/8/2 23:54:28

个人主页 ： zxctscl
专栏【C++】、【C语言】、【Linux】、【数据结构】、【算法】
如有转载请先通知

文章目录

前言
1 2331. 计算布尔二叉树的值
- 1.1 分析
- 1.2 代码
2 129. 求根节点到叶节点数字之和
- 2.1 分析
- 2.2 代码
3 814. 二叉树剪枝
- 3.1 分析
- 3.2 代码
4 98. 验证二叉搜索树
- 4.1 分析
- 4.2 代码
5 230. 二叉搜索树中第 K 小的元素
- 5.1 分析
- 5.2 代码
6 257. 二叉树的所有路径
- 6.1 分析
- 6.2 代码

前言

上一篇提到递归、搜索和回溯介绍：【递归、搜索和回溯】递归、搜索和回溯介绍及递归类算法例题，继续来看着类型的题目

1 2331. 计算布尔二叉树的值

在这里插入图片描述

1.1 分析

看一下例一：把数字按题目换算成符号就是图片右边这样的情况，false&true=false，true|false=true。最后结果结果就是true。
在这里插入图片描述
算法原理：递归（dfs）
重复子问题：
主问题就是这棵树是true还是false，左子树是true还是false，把左子树传过去；右子树是true还是false，把右子树传过去。函数头bool dfs(root)

函数体：bool left=dfs(root->left);bool right=dfs(root->right)；再把左右子树按规则计算

出口：遇到叶子节点就返回结果

1.2 代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool evaluateTree(TreeNode* root) {if(root->left==nullptr)return root->val==0?false:true;bool left=evaluateTree(root->left);bool right=evaluateTree(root->right);return root->val==2?left|right:left&right;}
};

2 129. 求根节点到叶节点数字之和

在这里插入图片描述

2.1 分析

算法：递归
函数头：
传一个节点，计算与它相连的所有叶子结点的和
int dfs(root,presum)

函数体：计算节点5的值，那么第一步就得拿到到5时前面的值，也就是125，第二步，拿到它左子树值1258，第三步拿到它右子树的值12594+125931=138525，第四步，将左右两边相加1258+138525
在这里插入图片描述

递归出口：叶子结点

2.2 代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int sumNumbers(TreeNode* root) {return dfs(root,0);}int dfs(TreeNode* root,int presum){presum=presum*10+root->val;if(root->left==nullptr&&root->right==nullptr)return presum;int ret=0;if(root->left)ret+=dfs(root->left,presum);if(root->right)ret+=dfs(root->right,presum);return ret;}
};

3 814. 二叉树剪枝

在这里插入图片描述

3.1 分析

里面所有包含0的子树全部剪掉
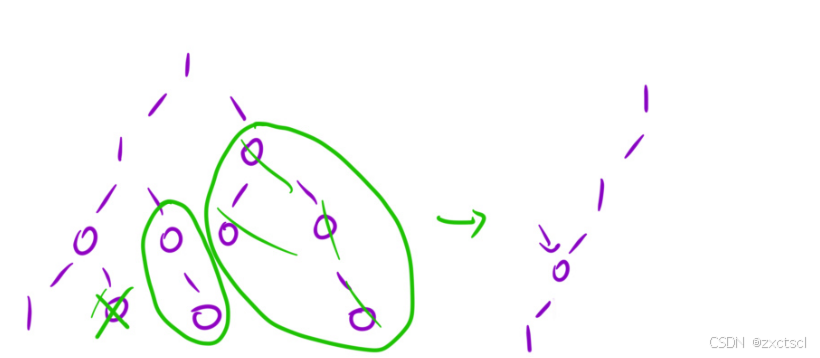
在这里插入图片描述
算法原理：递归
通过决策树，抽象出递归的三个核心问题

遇到0的时候，要先判断它的左子树和右子树是否是0，就要用到后序遍历。
当后序遍历节点的左子树遇到0后用null返回，如果左子树没有改变，就直接返回它的值。
在这里插入图片描述
函数头 Node* dfs(root)

函数体
（1）处理左子树
（2）处理右子树
（3）判断

递归出口
当root为空就返回

3.2 代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* pruneTree(TreeNode* root) {if(root==nullptr)return nullptr;root->left=pruneTree(root->left);root->right=pruneTree(root->right);if(root->left==nullptr&&root->right==nullptr&&root->val==0){root=nullptr;}return root;}
};

4 98. 验证二叉搜索树

在这里插入图片描述

4.1 分析

二叉搜索树的中序遍历的结果，是一个有序的序列用这个性质来做这道题。

用一个全局变量prev，让这个全局变量先初始化为负无穷大，当在进行中序遍历的时候，到一个节点的时候，prev记录它的前面遍历节点的值，拿prev和当前节点的值比较后，更新prev的值，继续遍历，是有序的就继续遍历，更新。
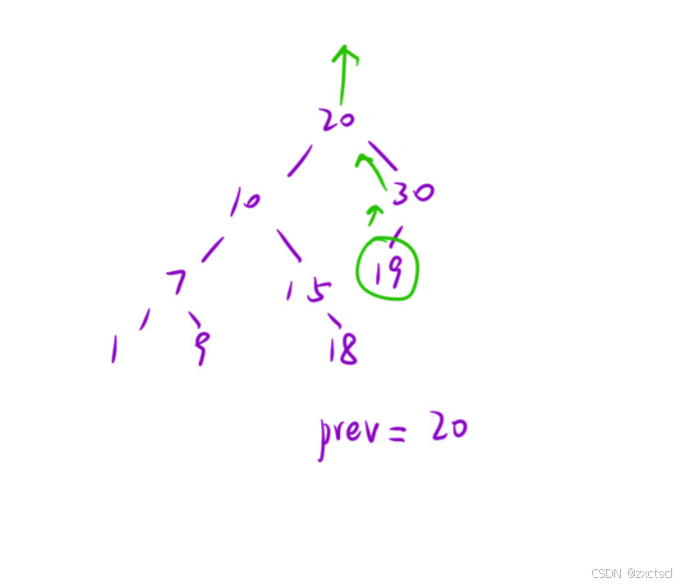
在这里插入图片描述

算法：递归
策略一：
左子树是二叉搜索树
当前节点符合二叉搜索树
右节点是二叉搜索树

策略二：剪枝
当全局变量prev，遍历到19的时候就已经不是二叉搜索树了，就不需要再往下遍历了。
在这里插入图片描述

4.2 代码

策略一：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution 
{long prev=LONG_MIN;
public:bool isValidBST(TreeNode* root) {if(root==nullptr)return true;bool left=isValidBST(root->left);bool cur=false;if(root->val>prev){cur=true;      }prev=root->val;bool right=isValidBST(root->right);return left&&right&&cur;}};

策略二：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution 
{long prev=LONG_MIN;
public:bool isValidBST(TreeNode* root) {if(root==nullptr)return true;bool left=isValidBST(root->left);if(left==false)return false;bool cur=false;if(root->val>prev){cur=true;      }prev=root->val;bool right=isValidBST(root->right);return left&&right&&cur;}};

5 230. 二叉搜索树中第 K 小的元素

在这里插入图片描述

5.1 分析

二叉搜索树的中序遍历的结果，是一个有序的序列用这个性质来做这道题。
与上面那题类似。
这题用两个全局变量和中序遍历。

一个全局变量c用来计数，另一个ret用来记录遍历节点对应的值。
每遍历一次c就减减，当c等于0时候的ret值就是最终需要的值。
当找到最终结果时候，此时c=0后面就不用遍历了。
在这里插入图片描述

5.2 代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {int count;int ret;
public:int kthSmallest(TreeNode* root, int k) {count=k;dfs(root);return ret;       }void dfs(TreeNode* root){if(root==nullptr||count==0)return;dfs(root->left);count--;if(count==0)ret=root->val;dfs(root->right);}
};

6 257. 二叉树的所有路径

在这里插入图片描述

6.1 分析

全局变量

回溯->恢复现场
一道题出现了回溯才能想到恢复现场。

题目要求以箭头形式返回结果

算法原理：
根节点开始向下搜索，遇到一个叶子结点，存一下这个路径，存到数组中返回。

用两个全局变量，一个string[] ret表示字符串数组保存最终结果，遇到一个叶子结点路径就放进去。另一个string path用来记录路径，遇到不是叶子结点就在后面加上这个值，遇到叶子结点后，把这个path加到ret里面。

但要考虑path的回溯问题：
为了防止回溯多加上叶子结点的值，就得恢复现场，再回溯时候就得剪掉上一个路径的叶子结点。
全局变量恢复现场不容易，就不用全局的string path。
在这里插入图片描述
如果把path设置成函数头参数，就不用恢复现场，函数的特性就会帮助恢复现场。

函数头：
void dfs(root,path)
当遍历时候，就会重新创建一个path，而上面的path也在：
在这里插入图片描述
函数体
当遇到叶子结点时：就把path加到ret里面
不是叶子结点就继续遍历

递归出口:
当左子树为空的时候，就不需要遍历它左子树，把它左子树就剪掉。
在这里插入图片描述
不想剪枝，就直接root为空返回

6.2 代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<string> ret;vector<string> binaryTreePaths(TreeNode* root) {string path;if(root==nullptr)return ret;dfs(root,path);return ret;}void dfs(TreeNode* root,string path){path+=to_string(root->val);if(root->left==nullptr&&root->right==nullptr){ret.push_back(path);return;}path+="->";if(root->left)dfs(root->left,path);if(root->right)dfs(root->right,path);}
};

有问题请指出，大家一起进步！！！

文章目录

前言

1 2331. 计算布尔二叉树的值

1.1 分析

1.2 代码

2 129. 求根节点到叶节点数字之和

2.1 分析

2.2 代码

3 814. 二叉树剪枝

3.1 分析

3.2 代码

4 98. 验证二叉搜索树

4.1 分析

4.2 代码

5 230. 二叉搜索树中第 K 小的元素

5.1 分析

5.2 代码

6 257. 二叉树的所有路径

6.1 分析

6.2 代码

相关文章：