【深度学习】#10 注意力机制
主要参考学习资料:
《动手学深度学习》阿斯顿·张 等 著
【动手学深度学习 PyTorch版】哔哩哔哩@跟李牧学AI
目录
- 注意力提示
- 生物学中的注意力提示
- 查询、键和值
- 注意力汇聚
- 注意力评分函数
- 掩蔽softmax操作
- 加性注意力
- 缩放点积注意力
- Bahdanau注意力
- 多头注意力
- 自注意力和位置编码
- 自注意力
- 位置编码
- 1. 绝对位置信息
- 2. 相对位置信息
- Transformer
- 编码器-解码器
- 逐位前馈网络(FFN)
- 层规范化(LR)
概述
- 注意力汇聚结合当前位置的预测任务自主地为不同输入分配权重。
- 输入的权重由相关性决定,计算相关性的函数称为注意力评分函数。
- Bahdanau注意力是注意力机制在Seq2Seq模型中的应用。
- 多头注意力对同一组信息分别做不同的注意力汇聚再组合。
- 自注意力计算同一序列内部任意两个元素的关系。
- Transformer是一种完全基于注意力机制的模型。
注意力提示
生物学中的注意力提示
人类每时每刻会接收大量的感官输入,这些感官输入远远超出了大脑能够完全处理的能力。但是并非所有刺激的影响都是同等的,意识的汇聚和专注使我们能够在复杂的环境中将注意力引向感兴趣的物体。
注意力的焦点受非自主性提示和自主性提示影响。非自主性提示基于环境中物体的突出性和易见性,例如人群中偶然出现身着奇装异服的人会吸引我们的目光;自主性提示受认知和意识的控制,例如我们想在人群中找到自己的朋友,会主动留意具有与朋友相关特征的事物。
查询、键和值
注意力机制是基于自主性提示的。在注意力机制中,自主性提示被称为查询,而感官输入被称为值,键是从感官输入中提取的特征表示,为非自主性提示,键和值是一一对应的。针对当前的预测任务,模型会先给出一个查询,通过将查询与每个键匹配判断每个值与查询的相关性,进而通过注意力汇聚为值赋予不同的权重,最终将值加权得到为当前预测任务提供参考的上下文变量。以论文写作中的文献查找为例,查询就是我们的研究任务,键就是我们在初步判断文献相关性时关注的标题和摘要,而值是文献具体的文章内容。

注意力汇聚
查询和键之间的交互形成了注意力汇聚,注意力汇聚有选择性地汇聚了值以生成最终的输出。Nadaraya-Watson核回归是一种常用的注意力汇聚方法。
一个比较通用的注意力汇聚公式形式如下:
f ( x ) = ∑ i = 1 n α ( x , x i ) y i f(x)=\displaystyle\sum^n_{i=1}\alpha(x,x_i)y_i f(x)=i=1∑nα(x,xi)yi
其中 x x x是查询, ( x i , y i ) (x_i,y_i) (xi,yi)是键值对。 α ( x , x i ) \alpha(x,x_i) α(x,xi)是分配给值 y i y_i yi的注意力权重,通过 x x x和 x i x_i xi的相关性得到。最后使用注意力权重对值进行加权和得到输出。权重是非负的,且总和为 1 1 1。
注意力权重通常使用核函数计算,它是数学中可用于衡量样本相似性的函数。Nadaraya-Watson核回归使用了高斯核,其定义为:
K ( x , x i ) = 1 2 π exp ( − ( x − x i ) 2 2 ) K(x,x_i)=\displaystyle\frac1{\sqrt{2\pi}}\exp\left(-\frac{(x-x_i)^2}2\right) K(x,xi)=2π1exp(−2(x−xi)2)
x x x和 x i x_i xi越相关(距离越近),则该核函数越接近 1 2 π \displaystyle\frac1{\sqrt{2\pi}} 2π1,反之则趋向于 0 0 0。
为了得到注意力权重,我们还需对其进行归一化处理:
α ( x , x i ) = exp ( − 1 2 ( x − x i ) 2 ) ∑ j = 1 n exp ( − 1 2 ( x − x j ) 2 ) = s o f t m a x ( − 1 2 ( x − x i ) 2 ) \alpha(x,x_i)=\displaystyle\frac{\displaystyle\exp\left(-\frac12(x-x_i)^2\right)}{\displaystyle\sum^n_{j=1}\exp\left(-\frac12(x-x_j)^2\right)}=\mathrm{softmax}\left(-\frac12(x-x_i)^2\right) α(x,xi)=j=1∑nexp(−21(x−xj)2)exp(−21(x−xi)2)=softmax(−21(x−xi)2)
最后我们得到基于Nadaraya-Waston核回归的注意力汇聚模型为:
f ( x ) = ∑ i = 1 n s o f t m a x ( − 1 2 ( x − x i ) 2 ) y i f(x)=\displaystyle\sum^n_{i=1}\mathrm{softmax}\left(-\frac12(x-x_i)^2\right)y_i f(x)=i=1∑nsoftmax(−21(x−xi)2)yi
该非参数的注意力汇聚模型需要大量数据才能收敛到最优结果,通过将查询 x x x和键 x i x_i xi之间的距离乘以可学习参数 w w w可以提升其泛化能力:
f ( x ) = ∑ i = 1 n s o f t m a x ( − 1 2 ( ( x − x i ) w ) 2 ) y i f(x)=\displaystyle\sum^n_{i=1}\mathrm{softmax}\left(-\frac12((x-x_i)w)^2\right)y_i f(x)=i=1∑nsoftmax(−21((x−xi)w)2)yi
注意力评分函数
在注意力汇聚模型中,最核心的组件是其softmax操作中的部分,被称为注意力评分函数,简称评分函数。评分函数是未经标准化的注意力权重,决定了模型如何聚焦于输入的不同部分,其设计直接影响模型的性能。

用数学语言描述,假设有一个查询 q ∈ R q \mathbf q\in\mathbb R^q q∈Rq和 m m m个键值对 ( k 1 , v 1 ) , ⋯ ( k m , v m ) (\mathbf k_1,\mathbf v_1),\cdots(\mathbf k_m,\mathbf v_m) (k1,v1),⋯(km,vm),其中 k ∈ R k \mathbf k\in\mathbb R^k k∈Rk, v ∈ R v \mathbf v\in\mathbb R^v v∈Rv。则注意力函数 f f f为值的加权和:
f ( q , ( k 1 , v 1 ) , … , ( k m , v m ) ) = ∑ i = 1 m α ( q , k i ) v i ∈ R v \displaystyle f(\mathbf{q}, (\mathbf{k}_1, \mathbf{v}_1), \ldots, (\mathbf{k}_m, \mathbf{v}_m)) = \sum_{i=1}^m \alpha(\mathbf{q}, \mathbf{k}_i) \mathbf{v}_i \in \mathbb{R}^v f(q,(k1,v1),…,(km,vm))=i=1∑mα(q,ki)vi∈Rv
其中权重由注意力评分函数 a a a经过softmax运算得到:
α ( q , k i ) = s o f t m a x ( a ( q , k i ) ) ∈ R \alpha(\mathbf{q}, \mathbf{k}_i) = \mathrm{softmax}(a(\mathbf{q}, \mathbf{k}_i))\in \mathbb{R} α(q,ki)=softmax(a(q,ki))∈R
掩蔽softmax操作
在某些情况下,并非所有的值都应该被纳入注意力汇聚中,例如为了进行小批量处理而将序列填充至等长的无意义词元。可以通过指定一个有效序列长度,在计算softmax时过滤掉超出指定范围的位置,称为掩蔽softmax操作。
加性注意力
加性注意力适用于查询和键的向量长度不一致的情况。给定查询 q ∈ R q \mathbf q\in\mathbb R^q q∈Rq和键 k ∈ R k \mathbf k\in\mathbb R^k k∈Rk,加性注意力的评分函数为:
a ( q , k ) = w v ⊤ tanh ( W q q + W k k ) ∈ R a(\mathbf q, \mathbf k) = \mathbf w_v^\top \text{tanh}(\mathbf W_q\mathbf q + \mathbf W_k \mathbf k) \in \mathbb{R} a(q,k)=wv⊤tanh(Wqq+Wkk)∈R
式中可学习的参数为 W q ∈ R h × q \mathbf W_q\in\mathbb R^{h\times q} Wq∈Rh×q、 W k ∈ R h × k \mathbf W_k\in\mathbb R^{h\times k} Wk∈Rh×k和 w v ∈ R h \mathbf w_v\in\mathbb R^h wv∈Rh。该函数将查询和键连接后送入激活函数为tanh的隐藏层得到一个长度为 h h h的向量后与 w v \mathbf w_v wv点积,超参数 h h h为隐藏单元数。
缩放点积注意力
在查询和键具有相同的长度 d d d时,点积可以得到计算效率更高的评分函数。假设查询和键的所有元素都是满足零均值和单位方差的独立的随机变量,则查询和键的点积的均值为 0 0 0,方差为 d d d。为确保点积的方差与向量无关,始终为 1 1 1,我们将点积除以 d \sqrt d d得到缩放点积注意力:
a ( q , k ) = q ⊤ k / d a(\mathbf q, \mathbf k) = \mathbf{q}^\top \mathbf{k} /\sqrt{d} a(q,k)=q⊤k/d
Bahdanau注意力
在上一章的机器翻译问题中,编码器将长度可变的序列转换为固定形状的上下文向量,而解码器根据上一个时间步输出的词元和上下文向量生成新输出的词元,每个词元的预测都使用相同的上下文向量。这种方法的缺点是无法处理较长的句子和捕获复杂的依赖关系。而且在翻译中,生成的词元往往和原句的词元存在一定的对应关系,每一步预测关注的输入词元是不一样的。
Bahdanau等人通过将上下文变量视为注意力汇聚的输出,实现了没有严格对齐限制的可微注意力模型。该模型基于上一章的Seq2Seq模型,只是上下文变量由固定不变的 c \mathbf c c变为每个解码时间步 t ′ t' t′都不一样的 c t ′ \mathbf c_{t'} ct′,它是注意力汇聚的输出:
c t ′ = ∑ t = 1 T α ( s t ′ − 1 , h t ) h t \displaystyle\mathbf{c}_{t'} = \sum_{t=1}^T \alpha(\mathbf{s}_{t' - 1}, \mathbf{h}_t) \mathbf{h}_t ct′=t=1∑Tα(st′−1,ht)ht
其中,查询是时间步 t ′ − 1 t'-1 t′−1的解码器隐状态 s t ′ − 1 \mathbf s_{t'-1} st′−1,键和值均为编码器隐状态 h t \mathbf h_t ht,注意力权重使用加性注意力计算。
使用注意力机制的编码器-解码器架构如下图所示(嵌入层对词元的独热向量表示作进一步处理,将在第十四章讨论):

多头注意力
在实践中,当给定相同的查询、键和值的集合时,我们希望模型可以基于相同的注意力机制学习不同的行为,然后将不同的行为作为知识组合起来,捕获序列内各种范围的依赖关系。为此,与其只使用一个注意力汇聚,我们可以将查询、键和值通过不同的线性映射得到 h h h组不同的集合,分别送入不同的注意力汇聚中,最后将它们的输出连接在一起,并再通过一个全连接层变换生成最终的输出:

这种设计被称为多头注意力,每个注意力汇聚被称为一个头。给定查询 q ∈ R d q \mathbf q\in\mathbb R^{d_q} q∈Rdq、键 k ∈ R d k \mathbf k\in\mathbb R^{d_k} k∈Rdk和值 v ∈ R d v \mathbf v\in\mathbb R^{d_v} v∈Rdv,每个注意力头 h i ( i = 1 , ⋯ , h ) \mathbf h_i(i=1,\cdots,h) hi(i=1,⋯,h)的计算方法为:
h i = f ( W i ( q ) q , W i ( k ) k , W i ( v ) v ) ∈ R p v \mathbf{h}_i = f(\mathbf W_i^{(q)}\mathbf q, \mathbf W_i^{(k)}\mathbf k,\mathbf W_i^{(v)}\mathbf v) \in \mathbb R^{p_v} hi=f(Wi(q)q,Wi(k)k,Wi(v)v)∈Rpv
其中可学习的参数包括全连接层的 W i ( q ) ∈ R p q × d q \mathbf W_i^{(q)}\in\mathbb R^{p_q\times d_q} Wi(q)∈Rpq×dq、 W i ( k ) ∈ R p k × d k \mathbf W_i^{(k)}\in\mathbb R^{p_k\times d_k} Wi(k)∈Rpk×dk和 W i ( v ) ∈ R p v × d v \mathbf W_i^{(v)}\in\mathbb R^{p_v\times d_v} Wi(v)∈Rpv×dv,以及注意力汇聚函数 f f f中的参数。带下标的 d d d和 p p p分别是全连接层转换前后的查询、键、值的长度, f f f可以是加性注意力或缩放点积注意力。
将 h h h个头的输出连接起来,并乘以可学习的参数 W o ∈ R p o × h p v \mathbf W_o\in\mathbb R^{p_o\times h p_v} Wo∈Rpo×hpv,我们就得到了多头注意力的最终输出:
W o [ h 1 ⋮ h h ] ∈ R p o \mathbf W_o \begin{bmatrix}\mathbf h_1\\\vdots\\\mathbf h_h\end{bmatrix} \in \mathbb{R}^{p_o} Wo h1⋮hh ∈Rpo
自注意力和位置编码
使用传统注意力机制的Seq2Seq模型仍存在以下问题:
- 每个时间步的计算都依赖前一个时间步的输出,无法并行化处理,只能逐个时间步地串行计算。
- 当序列较长的时候,容易出现梯度消失和梯度爆炸的问题。
因此进一步改进的方向是让模型不使用序列框架,但仍能有处理序列数据的能力,并且避免过长的链式求导过程。达成这个目标的最后一块拼图便是自注意力。
自注意力
自注意力和传统注意力相比,不计算序列之间的交互,而是计算同一序列内部的交互,直接捕捉序列中任意两个元素的关系,不像CNN和RNN一样受局部性限制。

在自注意力中,查询、键和值均为输入序列每一个时间步的输入。给定一个由词元组成的输入序列 x 1 , ⋯ , x n \mathbf{x}_1, \cdots, \mathbf{x}_n x1,⋯,xn,其中任意 x i ∈ R d ( 1 ⩽ i ⩽ n ) \mathbf x_i\in\mathbb R^d(1\leqslant i\leqslant n) xi∈Rd(1⩽i⩽n),该序列的自注意力输出为一个长度相同的序列 y 1 , ⋯ , y n \mathbf{y}_1, \cdots, \mathbf{y}_n y1,⋯,yn,其中:
y i = f ( x i , ( x 1 , x 1 ) , ⋯ , ( x n , x n ) ) ∈ R d \mathbf{y}_i = f(\mathbf{x}_i, (\mathbf{x}_1, \mathbf{x}_1), \cdots, (\mathbf{x}_n, \mathbf{x}_n)) \in \mathbb{R}^d yi=f(xi,(x1,x1),⋯,(xn,xn))∈Rd
上式中,键值对是每一个时间步的输入,时间步 i i i的输出 y i \mathbf y_i yi的查询为 x i \mathbf x_i xi。自注意力计算时间步 i i i的输入 x i \mathbf x_i xi与序列中所有时间步的输入的相关性,并对所有时间步的输入加权后经注意力汇聚 f f f处理得到输出 y i \mathbf y_i yi。
通过与CNN和RNN的比较可以理解自注意力的优势:

为了更加直观,对于CNN,我们将输入和卷积核均展成一维。对于长度为 n n n的序列和通道(特征)数均为 d d d的输入输出,三种网络的性能分别如下(CNN卷积核大小为 k k k):
| CNN | RNN | 自注意力 | |
|---|---|---|---|
| 计算复杂度 | O ( k n d 2 ) O(knd^2) O(knd2) | O ( n d 2 ) O(nd^2) O(nd2) | O ( n 2 d ) O(n^2d) O(n2d) |
| 最长路径 | O ( n / k ) O(n/k) O(n/k) | O ( n ) O(n) O(n) | O ( 1 ) O(1) O(1) |
| 并行度 | O ( n ) O(n) O(n) | O ( 1 ) O(1) O(1) | O ( n ) O(n) O(n) |
其中最长路径指输入序列中的一个输入能够传递给另一个输入(得到两个输入的相关信息)经过的计算链条长度,并行度指最多可以并行计算的数据量。
可见,CNN和自注意力都具有并行计算的优势,且自注意力的最长路径最短。但自注意力的计算复杂度是序列长度的平方,因此对很长的序列计算效率较低。
位置编码
CNN和RNN均通过更复杂模型的机制利用了序列输入的位置信息,而自注意力只是一次性接收所有输入对它们全部加权,替换输入的位置顺序不会对输入有影响。为了在不让模型更加复杂的限制下使用序列的位置信息,我们向输入表示中添加位置编码来注入相对或绝对的位置信息,而模型需要通过训练学习到输入表示中的位置信息。
简单地添加表示序号的整数会带来一些问题,主要在于编号缺少限制,对于长文本而言,过大的数字会导致模型在学习词义时受到干扰,或产生数值爆炸,文本的长短不一也会给模型的泛化带来困难。
一个有效的位置编码应该在保证每个输入有唯一表示的同时可以无限延伸而不会爆炸,而傅里叶变换的正余弦组合表示正好符合条件,因为三角函数的周期 2 π 2\pi 2π为无理数,所有有理数的三角函数严格唯一。假设输入表示 X ∈ R n × d \mathbf{X} \in \mathbb{R}^{n \times d} X∈Rn×d包含一个序列中 n n n个词元的 d d d维表示,位置编码则使用相同形状的位置嵌入矩阵 P ∈ R n × d \mathbf{P} \in \mathbb{R}^{n \times d} P∈Rn×d与之相加(或连接),矩阵第 i i i行、第 2 j 2j 2j列和第 2 j + 1 2j+1 2j+1列上的元素分别为:
p i , 2 j = sin ( i 1000 0 2 j / d ) \displaystyle p_{i, 2j} = \sin\left(\frac{i}{10000^{2j/d}}\right) pi,2j=sin(100002j/di)
p i , 2 j + 1 = cos ( i 1000 0 2 j / d ) \displaystyle p_{i, 2j+1} = \cos\left(\frac{i}{10000^{2j/d}}\right) pi,2j+1=cos(100002j/di)
1. 绝对位置信息
通过线图和热力图我们可以对矩阵在不同行(位置)和不同列(特征)的值进行可视化:

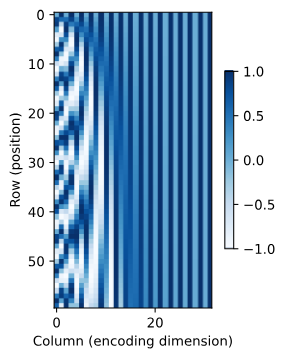
从图中可以看出,输入序列中不同特征的位置编码会随着位置的变化以不同频率波动,多维频率和三角函数的无理数性质共同保证了位置编码的唯一性。同时,低频的特征变化缓慢,便于捕捉长距离关系;高频的特征变化剧烈,便于捕捉细粒度位置。
2. 相对位置信息
该位置编码还能让模型学习到输入序列中的相对位置信息,因为对于一定的偏移量,偏移后位置表示可以转换为对原位置编码的线性组合:
[ p i + δ , 2 j p i + δ , 2 j + 1 ] = [ sin ( ( i + δ ) ω j ) cos ( ( i + δ ) ω j ) ] = [ cos ( δ ω j ) sin ( i ω j ) + sin ( δ ω j ) cos ( i ω j ) − sin ( δ ω j ) sin ( i ω j ) + cos ( δ ω j ) cos ( i ω j ) ] = [ cos ( δ ω j ) sin ( δ ω j ) − sin ( δ ω j ) cos ( δ ω j ) ] [ p i , 2 j p i , 2 j + 1 ] \begin{split}\begin{aligned} &\begin{bmatrix} p_{i+\delta, 2j} \\ p_{i+\delta, 2j+1} \\ \end{bmatrix}\\ =&\begin{bmatrix} \sin\left((i+\delta) \omega_j\right) \\ \cos\left((i+\delta) \omega_j\right) \\ \end{bmatrix}\\ =&\begin{bmatrix} \cos(\delta \omega_j) \sin(i \omega_j) + \sin(\delta \omega_j) \cos(i \omega_j) \\ -\sin(\delta \omega_j) \sin(i \omega_j) + \cos(\delta \omega_j) \cos(i \omega_j) \\ \end{bmatrix}\\ =&\begin{bmatrix} \cos(\delta \omega_j) & \sin(\delta \omega_j) \\ -\sin(\delta \omega_j) & \cos(\delta \omega_j) \\ \end{bmatrix} \begin{bmatrix} p_{i, 2j} \\ p_{i, 2j+1} \\ \end{bmatrix}\\ \end{aligned}\end{split} ===[pi+δ,2jpi+δ,2j+1][sin((i+δ)ωj)cos((i+δ)ωj)][cos(δωj)sin(iωj)+sin(δωj)cos(iωj)−sin(δωj)sin(iωj)+cos(δωj)cos(iωj)][cos(δωj)−sin(δωj)sin(δωj)cos(δωj)][pi,2jpi,2j+1]
Transformer
自注意力的并行计算和最短最长路径使其在设计深度网络架构上具有很大的优势。Transformer模型采用编码器-解码器架构,但是和使用注意力的Seq2Seq不同,它是一种完全基于注意力机制的模型。

编码器-解码器
Transformer的编码器和解码器分别接收源(输入)序列和目标(输出)序列的嵌入表示与位置编码的和作为输入。
编码器由多个相同的层叠加而成,每个层都有多头自注意力汇聚和逐位前馈网络两个子层。受残差网络启发,每个子层都采用了残差连接,紧接着应用层规范化。残差连接要求对于输入序列对应的每个位置 x ∈ R d \mathbf x\in\mathbb R^d x∈Rd,Transformer编码器都将输出一个 d d d维表示向量。
解码器也由多个相同的层叠加而成,其在编码器中两个子层的基础上插入了第三个子层,称为编码器-解码器注意力层。在编码器-解码器注意力层中,查询来自前一个解码器层的输出,而键和值来自整个编码器的输出。而在处理来自目标序列的输入时,解码器的多头自注意力只能考虑当前位置之前的所有位置,即计算 x i \mathbf x_i xi的输出 y i \mathbf y_i yi时,假装当前序列长度为 i i i,以确保当前的预测仅依赖已生成的输出词元,因此采取了掩蔽注意力。
逐位前馈网络(FFN)
在Transformer中,注意力一次性接收一整个序列而不是序列中每个时间步的词元作为输入,一个长度为 n n n、特征数为 d d d的序列样本的输入维度是 n × d n\times d n×d,然而序列长度 n n n是可变的,这让输入维度固定的全连接层无法直接处理一个样本。但是在批量化处理中,同一个全连接层可以处理不同批量大小 b b b的批量样本。
对于形状为 ( b , n , d ) (b,n,d) (b,n,d)一个批量的序列样本,我们可以将其变换成 ( b × n , d ) (b\times n,d) (b×n,d),把序列长度 n n n合并到批量大小 b b b中,则输入维度固定为 d d d。这相当于把序列拆散为词元,将词元视为一个样本处理。在全连接层处理过后,我们仍将其形状还原为 ( b , n , d ) (b,n,d) (b,n,d)。由于该网络逐个位置地处理词元,而不是直接处理整个序列,因此被称为逐位前馈网络。
层规范化(LR)
在之前介绍的批量规范化中,我们从特征维度上对一个批量的所有样本进行规范化,然而该方法无法处理可变序列输入。在逐位前馈网络中提到,直接对序列做批量化处理要求所有序列的长度一致,如果通过填充词元来实现这一点,则填充词元将扰乱批量规范化对其他词元的均值和方差的统计,影响模型收敛。同时,填充词元也会占用显存,产生更多的无效计算,尤其是自然语言处理的样本分布往往是少数序列极长,多数较短,将会有大量的序列被填充大量填充词元。
层规范化则从样本维度上独立地对每个样本的所有特征进行归一化,在无视批量的同时还保留了特征间关系,在序列处理模型中替代了批量规范化的地位。
总结一下,在Transformer中,源序列和目标序列经嵌入表示和位置编码相加分别作为编码器和解码器的输入。在编码器中,源序列的输入经多次自注意力汇聚、逐位前馈网络处理得到原始的上下文变量。在解码器的每个相同的层中,掩蔽注意力仅接收当前预测位置之前的目标序列,并将上一个位置的预测结果作为查询对来自编码器的原始上下文变量进行注意力汇聚操作,其输出送入逐位前馈网络。每个子层之间都采取了残差连接和层规范化处理。
相关文章:

【深度学习】#10 注意力机制
主要参考学习资料: 《动手学深度学习》阿斯顿张 等 著 【动手学深度学习 PyTorch版】哔哩哔哩跟李牧学AI 目录 注意力提示生物学中的注意力提示查询、键和值 注意力汇聚注意力评分函数掩蔽softmax操作加性注意力缩放点积注意力 Bahdanau注意力多头注意力自注意力和位…...

Modbus总线协议智能网关协议转换案例解析:提升系统兼容性
Modbus是一种串行通信协议,是Modicon公司(现在的施耐德电气,Schneider Electic)于1979年为使用可编程逻辑控制器(PLC)通信而发表。Modbus已经成为工业领域通信协议的业界标准(Defacto),并日现在是工业电子设备之间常用的连接方式 Modbus是一种串行通信协…...

echarts自定义图表--仪表盘
基于仪表盘类型的自定义表盘 上图为3层结构组成 正常一个仪表盘配置要在外圈和内圈之间制造一条缝隙间隔 再创建一个仪表盘配置 背景透明 进度条拉满 进度条颜色和数据的背景相同开始处的线 又一个仪表盘配置 数值固定一个比较小的值 <!DOCTYPE html> <html><h…...

第五章:Execution Flow Framework
Chapter 5: Execution Flow Framework 从消息记忆到执行流程:如何让多个AI“同事”协同完成复杂任务? 在上一章的消息与记忆系统中,我们已经能让AI记住之前的对话内容。但你是否想过:如果用户要求“预订从北京到上海的高铁&#…...

01 C++概述
一、C语言发展史 起源与演进 • 1960s:剑桥大学Martin Richards开发BCPL语言,用于系统软件开发。 • 1970年:贝尔实验室Ken Thompson在BCPL基础上发明B语言。 • 1972年:Dennis Ritchie和Brian Kernighan设计出C语言,兼…...

Kotlin DSL 深度解析:从 Groovy 迁移的困惑与突破
引言 Gradle 作为现代构建工具,支持 Groovy 和 Kotlin 两种 DSL(领域特定语言)。Kotlin DSL 因其类型安全和更好的 IDE 支持逐渐流行,但它的语法设计却让许多开发者感到困惑,尤其是从 Groovy 迁移时。 本文将从 Kotl…...

2025年二级造价师考点总结
二级造价师考点总结 一、建设工程造价管理 工程造价构成:重点掌握建筑安装工程费(人工费、材料费、机械费、企业管理费、利润、规费、税金)的组成及计算。 计价依据:熟悉工程量清单计价规范,掌握定额计价与清单计价的…...

Typecho博客使用阿里云cdn和oss:handsome主题进阶版
Typecho使用阿里云cdn和oss 设置前需要保证阿里云cdn和oss已配置好且可以正常使用一、准备工作二、修改 Handsome 主题的静态资源链接方法 1:直接修改主题文件(推荐)方法 2:通过主题设置自定义(方便) 三、处…...

知识体系_用户研究_用户体验度量模型
1 用户体验度量常见模型 1.1 满意度(CSAT/PSAT) CSAT(Customer Satisfaction)指客户满意度,PAST(Product Satisfaction)指产品满意度。顾名思义,其用于衡量客户对产品或服务的体验度量指标。在用户完成某个产品或某项服务的体验后,对其进行…...

邮件分类特征维度实验分析
活动发起人小虚竹 想对你说: 这是一个以写作博客为目的的创作活动,旨在鼓励大学生博主们挖掘自己的创作潜能,展现自己的写作才华。如果你是一位热爱写作的、想要展现自己创作才华的小伙伴,那么,快来参加吧!…...

Linux服务之Nginx服务部署及基础配置
目录 一.Nginx介绍 1.Nginx功能介绍 2.基础特性 3.Web服务相关的功能 4.I/O模型相关概念 5.nginx模块 6.Nginx文件存放位置 7.Nginx事件驱动模型 二.平滑升级及信号使用 1.Nginx 程序当作命令使用 2.信号类型 3.平滑升级nginx 4.回滚 三.Nginx调优 1.隐藏版本号或…...

Centos小白之在CentOS8.5中安装Rabbitmq 3.10.8
注意事项 安装以及运行等其他操作,要使用root账号进行,否则会遇到很多麻烦的事情。 使用命令行进行远程登录 ssh root192.168.0.167 安装make 执行安装命令 yum -y install make gcc gcc-c kernel-devel m4 ncurses-devel openssl-devel这里有可能会…...

基于单片机的游泳馆智能管理系统设计与实现
标题:基于单片机的游泳馆智能管理系统设计与实现 内容:1.摘要 随着游泳馆规模的不断扩大和管理需求的日益提高,传统的管理方式已难以满足高效、精准的管理要求。本文旨在设计并实现一种基于单片机的游泳馆智能管理系统。采用单片机作为核心控制单元,结合…...
——深度相机模型及用途介绍)
深度相机(一)——深度相机模型及用途介绍
一、深度相机概述 深度相机,又称 3D 相机,是一种能够获取场景中物体深度信息(即物体到相机的距离)的设备。与传统相机只能拍摄二维平面图像不同,深度相机不仅能记录物体的颜色和纹理,还能通过特定技术手段测…...

【Torch】nn.Conv1d、nn.Conv2d、nn.Conv3d算法详解
1. nn.Conv1d 1.1 输入(Input)和输出(Output) 输入张量 形状:(batch_size, in_channels, length) batch_size:一次过网络的样本数in_channels:每个样本的通道数(特征维度࿰…...

Android WebRTC回声消除
文章目录 安卓可用的回声消除手段各种回声消除技术优缺点WebRTC回声消除WebRTC回声消除回声消除处理流程WebRTC AECM APP 安卓可用的回声消除手段 硬件回声消除 使用 AudioRecord 的 VOICE_COMMUNICATION 模式:通过 AudioRecord 的 VOICE_COMMUNICATION 音频源可以…...

[Linux运维] [Ubuntu/Debian]在Lightsail Ubuntu服务器上安装Python环境的完整指南
在之前的教程中,我们已经讲过如何开通亚马逊Lightsail服务器并安装宝塔面板。今天,我们来进一步补充:如何在Lightsail上的Ubuntu/Debian系统中安装和配置Python开发环境。 本教程不仅适用于Lightsail服务器,也适用于所有使用Ubunt…...

2025医疗领域AI发展五大核心趋势与路线研究
引言 人工智能技术正在全球范围内深刻改变医疗服务的提供方式,推动全球医疗的普惠化、技术合作、产业升级以及公共卫生防控发生巨变[0]。医疗AI的浪潮奔涌向前,从2024年开始,生成式AI的爆发式发展更是将医疗AI推到了新的十字路口[1]。在这一背景下,本报告将深入探讨医疗领…...
 | 第六周|过拟合问题)
【学习笔记】机器学习(Machine Learning) | 第六周|过拟合问题
机器学习(Machine Learning) 简要声明 基于吴恩达教授(Andrew Ng)课程视频 BiliBili课程资源 文章目录 机器学习(Machine Learning)简要声明 摘要过拟合与欠拟合问题一、回归问题中的过拟合1. 欠拟合(Underfit&#x…...

【MQ篇】RabbitMQ之惰性队列!
目录 引言:当“生产”大于“消费”,队列就“胖”了!肥宅快乐队列?🤔队列界的“躺平”大师:惰性队列(Lazy Queues)驾到!😴如何“激活”你的队列的“惰性”属性…...

计算机视觉——通过 OWL-ViT 实现开放词汇对象检测
介绍 传统的对象检测模型大多是封闭词汇类型,只能识别有限的固定类别。增加新的类别需要大量的注释数据。然而,现实世界中的物体类别几乎无穷无尽,这就需要能够检测未知类别的开放式词汇类型。对比学习(Contrastive Learning&…...
)
第二部分:网页的妆容 —— CSS(下)
目录 6 布局基础:Display 与 Position - 元素如何排列和定位6.1 小例子6.2 练习 7 Flexbox 弹性布局:一维布局利器7.1 小例子7.2 练习 8 Grid 网格布局:强大的二维布局系统8.1 小例子8.2 练习 9 响应式设计与媒体查询:适应不同设备…...

vite项目tailwindcss4的使用
1、安装taillandcss 前几天接手了一个项目,看到别人用tailwindcss节省了很多css代码的编写,所以自己也想在公司项目中接入tailwindcss。 官网教程如下: Installing Tailwind CSS with Vite - Tailwind CSS 然而,我在vite中按…...

css中:is和:where 伪函数
在 CSS 里,:is() 属于伪类函数,其作用是对一组选择器进行匹配,只要元素与其中任何一个选择器相匹配,就可以应用对应的样式规则。以下是详细介绍: 基本语法 :is() 函数的参数是一个或多个选择器,各个选择器之…...

线下零售数据采集:在精度与效率之间寻找平衡点
线下零售数据采集:在精度与效率之间寻找平衡点 为什么线下零售必须重视数据采集? 随着零售行业竞争加剧,门店执行的标准化与透明化成为供应链协作、销售提升的基础工作。 POG(陈列执行规范)的落地效果、陈列策略的调整…...

【Robocorp实战指南】Python驱动的开源RPA框架
目录 前言技术背景与价值当前技术痛点解决方案概述目标读者说明 一、技术原理剖析核心概念图解核心作用讲解关键技术模块说明技术选型对比 二、实战演示环境配置要求核心代码实现案例1:网页数据抓取案例2:Excel报表生成 运行结果验证 三、性能对比测试方…...

新ubuntu物理机开启ipv6让外网访问
Ubuntu 物理机 SSH 远程连接与 IPv6 外网访问测试指南 1. 通过 SSH 远程连接 Ubuntu 物理机 1.1 安装 SSH 服务 sudo apt update sudo apt install openssh-server1.2 检查 SSH 服务状态 sudo systemctl status ssh确认出现 active (running)。 1.3 获取物理机 IP 地址 i…...

驱动开发硬核特训 │ Regulator 子系统全解
一、Regulator子系统概述 在 Linux 内核中,Regulator 子系统是专门用于管理电源开关、电压调整、电流控制的一套完整框架。 它主要解决以下问题: 设备需要的电压通常不一样,如何动态调整?有些设备休眠时需要关闭供电࿰…...
)
入门版 鸿蒙 组件导航 (Navigation)
入门版 鸿蒙 组件导航 (Navigation) 注意:使用 DevEco Studio 运行本案例,要使用模拟器,千万不要用预览器,预览器看看 Navigation 布局还是可以的 效果:点击首页(Index)跳转到页面(…...

怎样将visual studio 2015开发的项目 保存为2010版本使用
用的老旧电脑跑vs2015太慢了,实在忍不了了! 想把用 Visual Studio 2015 的做的项目保存为 Visual Studio 2010 兼容的格式,以后都使用2010写了。自己在网上搜了一下,亲测以下步骤可以的 手动修改解决方案和项目文件 修改解决方案…...

【学习笔记】软件测试流程-测试设计阶段
软件测试设计阶段这个阶段主要工作是编写测试用例。 什么是测试用例? 测试用例(TestCase)是为项目需求而编制的一组测试输入、执行条件以及预期结果,以便测试某个程序是否满足客户需求。简而言之,测试用例是每一个测…...

Rust 学习笔记:关于切片的两个练习题
Rust 学习笔记:关于切片的两个练习题 Rust 学习笔记:关于切片的两个练习题引用和切片引用的大小以下程序能否通过编译? Rust 学习笔记:关于切片的两个练习题 参考视频: https://www.bilibili.com/video/BV1GrDQYeEzS…...

BeeWorks企业内部即时通讯软件支持国产化,已在鸿蒙系统上稳定运行
一、企业用户面临的困境与痛点 一些企业用的即时通讯软件比较旧,存在的问题不仅影响了日常工作的正常开展,也阻碍了企业信息化建设的进程: ● 国产系统与移动端不兼容:仅支持Windows和MAC系统,无法在银河麒麟、统信U…...

java对文字按照语义切分
实现目标 把一段文本按照一个完整的一句话为单元进行切分。如:以逗号,感叹号结尾看作是一个句子。 实现方案 StanfordCoreNLP切分 引入依赖 <dependency><groupId>edu.stanford.nlp</groupId><artifactId>stanford-corenlp<…...

华纳云:centos如何实现JSP页面的动态加载
JSP(JavaServer Pages)作为Java生态中常用的服务器端网页技术,具有动态内容生成、可扩展性强、与Java无缝结合等优势。 而CentOS作为一款稳定、高效、安全的Linux服务器操作系统,非常适合部署JSP应用。 想要让JSP页面实现动态更新加载,避免…...
:会话+消息过期机制,设备远程控制,批量控制实现)
Android 消息队列之MQTT的使用(二):会话+消息过期机制,设备远程控制,批量控制实现
目录 一、实际应用场景 室内温湿度数据上传设备远程控制批量控制实现 二、会话管理、消息过期设置 4.1 会话管理 Clean Session参数 新旧会话模式对比典型应用场景 4.2 消息过期设置 MQTT 5.0消息过期机制 Message Expiry Interval属性QoS级别影响 三、实际应用场景 …...

一、JVM基础概念
一、JVM的设计目标 一次编译,到处运行(跨平台) ➔ Java编译成字节码,由JVM在不同平台解释/编译执行,实现跨平台。 内存管理与垃圾回收 ➔ JVM统一负责内存分配和回收,降低内存泄漏的风险。 性能优化 ➔ JIT(即时编译…...

深度学习---Pytorch概览
一、PyTorch 是什么? 1. 定义与定位 开源深度学习框架:由 Facebook(Meta)AI 实验室开发,基于 Lua 语言的 Torch 框架重构,2017 年正式开源,主打动态计算图和易用性。核心优势:灵活…...

第33周JavaSpringCloud微服务 分布式综合应用
第33周JavaSpringCloud微服务 分布式综合应用 一、分布式综合应用概述 分布式知识体系内容广泛,主要包括分布式事务、分布式锁、RabbitMQ等消息中间件的应用以及跨域问题的解决。 1.1 课程重点内容介绍 分布式事务 :在大型项目中普遍存在,…...

Paramiko 完全指南
目录 Paramiko 概述核心功能与模块框架安装与依赖基础用法与案例详解 SSH 连接与命令执行密钥认证SFTP 文件传输交互式会话端口转发 高级功能与实战技巧常见问题与解决方案总结与资源推荐 1. Paramiko 概述 是什么? Paramiko 是一个纯 Python 实现的 SSHv2 协议库…...
二进制部署教程(保姆级))
夜莺监控V8(Nightingale)二进制部署教程(保姆级)
夜莺监控部署 前置工作 1. 部署好mysql 2. 部署好redis 3. 部署好prometheus夜莺压缩包下载 本教程基于Centos7系统下的二进制方式部署,先去官网进行压缩包下载 在系统创建/opt/n9etest目录,并将压缩包拖进目录 mkdir /opt/n9etest进入/opt/n9etest࿰…...

鸿蒙应用开发 知识点 官网快速定位表
ArkTS 语言介绍 ArkTS 语言介绍 基础入门 资源分类与访问 添加组件(基础组件) 显示图片 (Image) 按钮 (Button) 单选框 (Radio) 切换按钮 (Toggle) 进度条 (Progress) 视频播放 (Video) 使用文本 文本显示 (Text/Span) 文本输入 (TextInput/TextArea) 使用弹窗 使用弹…...
的差异)
【神经网络与深度学习】两种加载 pickle 文件方式(joblib、pickle)的差异
引言 从深度学习应用到数据分析的多元化需求出发,Python 提供了丰富的工具和模块,其中 pickle 和 joblib 两种方式在加载数据文件方面表现尤为突出。不同场景对性能、兼容性以及后续处理的要求不尽相同,使得这两种方式各显优势。本文将通过深…...
)
quickbi finebi 测评(案例讲解)
quickbi & finebi 测评 国产BI中入门门槛比较低的有两个,分别是quickbi和finebi。根据我的经验通过这篇文章做一个关于这两款BI的测评文章。 quickbi分为个人版、高级版、专业版、私有化部署四种。这篇文章以quickbi高级版为例,对quickbi进行分享。…...

vue的生命周期 以及钩子
最早可以在created 时调用后端接口获取数据,因为beforecreated的时候 那个data 都还还是初始化出来 修改数据的时候触发 update 案例1:create 案例2:一进来页面获取搜索框焦点 echarts 饼图渲染 初始化dom后才去准备实例,所以必须要在dom之后…...

Mariadb 防火墙服务器和端口:mysql | 3306
Centos7 Mariadb 理解:Mariadb数据库就类似于我们生活中常见的Excel。 主要工作原理就是我们创造一个数据库其中创造一个数据表再在数据表中输入内容,分为三类。在详细点就是打开Excel(数据库),我们在其中加入…...
--web请求过程)
爬虫学习笔记(二)--web请求过程
Web请求全过程(重要) 从输入完网址(如输入百度网址)到返回页面以及页面中的数据这一完整的过程发生了什么事情? 服务器端渲染 在服务器端直接把数据和html整合,统一返回给浏览器,在页面源代码…...

开发vue项目所需要安装的依赖包
在开发Vue项目时,通常需要安装以下几个核心依赖包:1、Vue CLI、2、Vue Router、3、Vuex、4、Axios。这些依赖包可以确保你的Vue项目拥有基础的功能和良好的开发体验。接下来,我们将详细介绍每个依赖包的作用、安装方法以及使用案例。 一、VUE…...
——方法详解)
Java SE(4)——方法详解
1.方法的概念&使用 1.1 什么是方法? Java中的方法类似于C语言中的函数,是用于执行特定任务的代码块。 那么用方法组织起来的代码块和普通的代码相比有什么优势呢? 1.当代码规模较大且应用场景较为复杂时,方法能够模块化地组…...
)
网络安全实战指南:从安全巡检到权限维持的应急响应与木马查杀全(命令查收表)
目录 一、安全巡检的具体内容 1. 巡检的频率与目标是什么 2. 巡检的内容是什么以及巡检后如何加固 二、Windows环境下应急响应的主要流程 1. 流程概述及每个步骤详细解释 步骤1:隔离与遏制 步骤2:识别与分析 步骤3:清除与恢复 步骤4…...
