线性代数—向量与矩阵的范数(Norm)
参考链接:
范数(Norm)——定义、原理、分类、作用与应用 - 知乎
带你秒懂向量与矩阵的范数(Norm)_矩阵norm-CSDN博客
什么是范数(norm)?以及L1,L2范数的简单介绍_l1 norm-CSDN博客
范数(Norm)是线性代数中的一个基本概念,用来度量一个向量的“长度”或“大小”。
(简单来说,范数告诉我们一个向量离原点有多远。)
- 向量范数 表征 向量空间中向量的大小,
- 矩阵范数 表征 矩阵引起变化的大小。
在机器学习中,范数常用于:
- 衡量预测误差(损失函数)
- 控制模型参数(正则化)
- 比较向量之间的相似度(归一化)
不同范数对应不同的学习目标:
- L1 控稀疏;
- L2 控幅度;
- L∞ 控最大值。
引入范数的原因
我们都知道,函数与几何图形往往是有对应的关系,这个很好想象,特别是在三维以下的空间内,函数是几何图像的数学概括,而几何图像是函数的高度形象化。
但当函数与几何超出三维空间时,就难以获得较好的想象,于是就有了映射的概念,进而引入范数的概念。当有了范数的概念,就可以引出两个向量的距离的定义,这个向量可以是任意维数的。
通过距离的定义,进而我们可以讨论逼近程度,从而讨论收敛性、求极限。
- 范数在计算机领域多用于:迭代过程中收敛性质的判断。
- 一般迭代前后步骤的差值的范数表示其大小,常用的是二范数,差值越小表示越逼近实际值,可以认为达到要求的精度,收敛。
总的来说,范数存在的意义是为了实现比较距离。
比如,在一维实数集合中,我们随便取两个点4和9,我们知道9比4大。
但是到了二维实数空间中,取两个点(1,0)和(3,4),这个时候就没法比较它们之间的大小,因为它们不是可以比较的实数。
于是引入范数这个概念,把(1,0)和(3,4)通过范数分别映射到实数1 和 5 (两个点分别到原点的距离),这样我们就比较这两个点了。
所以可以看到,范数其实是一个函数,它把不能比较的向量转换成可以比较的实数。
数学原理

向量的范数
在数学上,对于向量范数的定义,就是只要满足以下三条性质的函数,我们就可以称为它为范数。

(条件1的 的意思就是当且仅当的意思)
所以,范数的是一个宽泛的概念,有很多种,但是一般只会用到常用的范数。
线性代数中最有用的一些运算符是范数(norm)。 非正式地说,向量的范数是表示一个向量有多大。 这里考虑的大小(size)概念不涉及维度,而是分量的大小。
在线性代数中,向量范数是将向量映射到标量的函数
。 给定任意向量x,向量范数要满足一些属性。
性质3&4即正定,性质1即齐次,性质2即三角不等性。
向量的 L0范数
意义:非0元素个数

评价:L0范数表示向量中非零元素的个数。
L0范数的这个属性,使其非常适用于机器学习中的稀疏编码。
在特征选择中,通过最小化L0范数来寻找最少最优的稀疏特征项。
但是,L0范数的最小化问题是NP难问题。而L1范数是L0范数的最优凸近似,它比L0范数要更容易求解。
因此,优化过程将会被转换为更高维的范数(例如L1范数)问题。
向量的 L1范数 (曼哈顿范数、、最小绝对误差)
意义:各个元素的绝对值之和(向量x中非零元素的绝对值之和)
几何意义:实际走的 “横+竖” 的 “城市街道” 距离。

使用 L1范数可以度量两个向量间的差异,如绝对误差和(Sum of Absolute Difference):

由于L1范数的天然性质,对L1优化的解是一个稀疏解,
因此L1范数也被叫做 “Lasso regularization”(稀疏规则算子)。
通过L1可以实现特征的稀疏,去掉一些没有信息的特征,例如在对用户的电影爱好做分类的时候,用户有100个特征,可能只有十几个特征是对分类有用的,大部分特征如身高体重等可能都是无用的,利用L1范数就可以过滤掉。
向量的 L2范数 (欧几里得范数)
意义:每个元素平方和再平方根
 即
即 
像L1范数一样,L2也可以度量两个向量间的差异,如平方差和(Sum of Squared Difference):

评价:L2范数是最常用的范数,比如用的最多的度量距离欧氏距离就是一种L2范数。
在回归里面,有人把加了L2范数项的回归c称为“岭回归”(Ridge Regression),有人也叫它“权值衰减(weight decay)”。
它被广泛的应用在解决机器学习里面的过拟合问题:
- 通常被用来做优化目标函数的正则化项,防止模型为了迎合训练集而过于复杂造成过拟合的情况,从而提高模型的泛化能力。
为什么L2范数可以防止过拟合?回答这个问题之前,我们得先看看L2范数实际上是什么。
L2范数是指向量各元素的平方和然后求平方根。我们让L2范数的规则项最小,可以使得的每个元素都很小,都接近于0(L1范数会让它等于0,而L2范数是接近于0),这是有很大的区别的。而越小的参数说明模型越简单,越简单的模型则越不容易产生过拟合现象。为什么越小的参数说明模型越简单?
因为当限制了参数很小,实际上就限制了多项式某些分量的影响很小,即 相当于减少参数个数。
向量的 Lp范数 (一般形式)
意义:每个元素p次方和再p次方根
- L0、L1、L2 都是Lp范数的特例,分别对应P=0、1、2的情况;
- 可调节p控制范数行为(越大越趋近于L∞,即最大范数)
 即
即 
向量的 ∞范数 (最大范数)
意义:向量的 Lp范数的 p取无限大,即为向量的无穷范数,主要被用来度量向量元素的最大值。
- 取向量中最大绝对值作为长度。
- 有时用于鲁棒性分析。
![]()
PS
L2范数其实就是向量的标准内积,向量的长度一定是范数,长度是范数的充分条件,但不是必要条件,也就是说,范数不一定就是向量的长度。由
长度定义的性质可知,满足长度的定义要符合平行四边形。
举一个反例就可以证明非必要性:向量L1范数不满足平行四边形法则(A=(0,1)、B=(1,0))。
由内积决定的长度具有更丰富的几何结构。
总结
简单总结一下就是:
- L1范数: 为x向量各个元素绝对值之和,也叫“稀疏规则算”(Lasso regularization)。
- 比如 向量A=[1,-1,3], 那么A的L1范数为 |1|+|-1|+|3|.
- L2范数: 为x向量各个元素平方和的1/2次方(即 元素平方和的开根号)。
- L2范数又称Euclidean范数或者Frobenius范数
- Lp范数: 为x向量各个元素绝对值p次方和的1/p次方。
使用机器学习方法解决实际问题时,通常用L1或L2范数做正则化(regularization),从而限制权值大小,减少过拟合风险。特别是在使用梯度下降来做目标函数优化时。
L1正则化产生稀疏的权值,L2正则化产生平滑的权值为什么会这样?
在支持向量机学习过程中,L1范数实际是一种对于成本函数求解最优的过程,因此,L1范数正则化通过向成本函数中添加L1范数,使得学习得到的结果满足稀疏化,从而方便提取特征。
- L1范数可以使权值稀疏,方便特征提取。
- L2范数可以防止过拟合,提升模型的泛化能力。
L1和L2正则先验分别服从什么分布
- L1是拉普拉斯分布。
- L2是高斯分布。
矩阵的范数
跟向量的范数定义类似,只不过矩阵的范数的性质比向量的范数性质多了一条相容性。
我们直接引出矩阵的范数定义:

矩阵范数的第三条性质也称为加法相容性,第四条是乘法相容性,前提都是矩阵之间可以进行加法或乘法的运算。
矩阵的 1-范数(列模)
意义:矩阵的 列向量的和 的最大值,即 A的每列元素绝对值之和 的最大值,也称为A的列范数。

矩阵的 2-范数(谱模)
意义: 矩阵的最大特征值的开平方,也称谱范数。
- 特征值相当于是两个维度的压缩,相当于是从矩阵的维度里面找到最大的。

矩阵的 ∞范数(行模)
意义:矩阵的 行向量的和 的最大值,即 A的每行元素绝对值之和 的最大值,也称为A的行范数。

矩阵的 F-范数
意义:Frobenius范数,即矩阵元素绝对值的平方和再开平方。类似于向量的L2范数。
 即
即 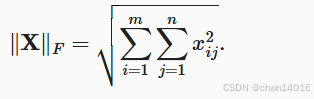
也可以描述为:

总结
简单总结一下就是:
- L1范数: 列范数,矩阵的 列向量的和 的最大值,即 A的每列元素绝对值之和 的最大值。
- L2范数:
矩阵的最大特征值的开平方,也称谱范数。
- 特征值相当于是两个维度的压缩,相当于是从矩阵的维度里面找到最大的。
- L∞范数: 行范数,矩阵的 行向量的和 的最大值,即 A的每行元素绝对值之和 的最大值。
- Lf范数: Frobenius范数,类似于向量的L2范数,矩阵元素平方和再开平方。
范数的作用
| 作用领域 | 用途 | 说明 |
|---|---|---|
| 向量距离 | 度量两个点或向量之间的“距离” | 用于损失函数、相似度计算 |
| 模型正则化 | 控制模型复杂度,防止过拟合 | 通过惩罚大参数避免学习噪声 |
| 向量归一化 | 把向量缩放到单位长度 | 常用于余弦相似度比较 |
| 稀疏表示 | 用最少的非零值表达信息 | L1 正则可自动“筛选特征” |
在机器学习中的实际应用
✅ 1. 损失函数中的误差度量
| 类型 | 范数 | 说明 |
|---|---|---|
| MAE(平均绝对误差) | L1 | 鲁棒,对异常值不敏感 |
| MSE(均方误差) | L2 | 常用,惩罚大误差更重 |
✅ 2. 模型正则化(Regularization)
| 类型 | 正则项 | 功能 |
|---|---|---|
| L1 正则(Lasso) | (\lambda \sum | \theta_i |
| L2 正则(Ridge) | λ∑θi2\lambda \sum \theta_i^2 | 缓和过拟合,不会让参数变0,但压小 |
✅ 3. 向量归一化(Normalization)

✅ 4. 稀疏建模(Sparse Modeling)
- 在某些应用中,希望模型只依赖少数几个特征(稀疏性):
- 如文本分类、基因数据分析;
使用 L1 正则可以“自动让不重要的参数变成 0”;
- L1 是稀疏性建模的核心工具。
面试范数相关常见提问汇总 + 答题思路
✅ 一、基础概念类问题(定义 + 原理)
❓Q1:解释一下什么是范数吗?
答题思路:
范数是一种用来衡量向量“大小”或“长度”的函数,它在机器学习中用于表示误差、距离、向量归一化或正则化。常见的范数有 L1 范数、L2 范数等,分别对应不同的应用需求。
❓Q2:L1 范数和 L2 范数的区别是什么?你更偏向哪一个?
答题思路:
- L1 范数是所有元素的绝对值之和,鼓励模型稀疏;
- L2 范数是所有元素平方和的平方根,鼓励整体平滑;
- 如果任务要求模型可解释性强、特征选择重要,我会选择 L1;
- 如果任务对稳定性更敏感,比如图像处理,我倾向 L2。
✅ 二、应用场景类问题(结合模型/正则)
❓Q3:在损失函数中为什么有时使用 L1 有时使用 L2?
答题思路:
- L1(如 MAE)更稳健,适合对异常值敏感的任务;
- L2(如 MSE)更常见,对大误差惩罚更重;
- 如果数据中有 outlier,建议使用 L1;
- 如果更关注整体误差稳定性,可以使用 L2。
❓Q4:正则化中 L1 和 L2 分别起什么作用?
答题思路:
- L1 正则通过绝对值惩罚,会使某些参数收缩为 0,实现特征选择;
- L2 正则通过平方惩罚,防止参数过大,减少过拟合;
- L1 更适合用于高维稀疏建模(如文本分类),L2 更适合神经网络等连续模型。
✅ 三、原理理解类问题(深入推导)
❓Q5:为什么 L2 正则不产生稀疏性,但 L1 会?
答题思路:
- 从几何角度讲,L1 范数的等值线是菱形,容易与损失函数的最优点交于坐标轴;
- 而 L2 范数的等值线是圆形,更倾向于“均匀缩小所有参数”而不是让某些为 0;
- 所以 L1 更容易“压掉”不重要的特征,让参数变为0。
❓Q6:你知道范数与梯度下降优化的关系吗?
答题思路:
- 在添加正则化的损失函数中,比如 L2,会影响梯度更新方向;
- L2 会加上 λθ\lambda \theta 项,等于对参数有一个“缩小”的趋势;
- L1 的梯度是非连续的(不可导点),所以常用次梯度或特殊优化方法处理。
✅ 四、项目/实践类问题(结合实际应用)
❓Q7:在项目中有没有用到范数?怎么选的 L1 / L2?
答题思路(举例):
- “在我做房价预测项目中,我使用了 L1 正则化进行特征选择,发现有多个冗余特征被自动归零,提升了模型解释性。”
- “而在另一个图像复原项目中,我使用了 L2 损失函数和 L2 正则,因为目标是尽可能还原每个像素值,不允许过大偏差。”
❓Q8:若模型过拟合了,会怎么用范数应对?
答题思路:
- 我会通过添加正则化项(L1/L2)来约束模型参数的规模;
- 如果模型很复杂,特征维度很高,我会尝试 L1 来让模型自动做特征选择;
- 如果我关注模型的稳定性和泛化性能,我会使用 L2 控制参数幅度。
✅ 五、开放性问题(考察综合素质)
❓Q9:如果我说 L2 正则是控制模型复杂度的“软剪枝”,你怎么理解?
答题思路:
- 软剪枝指的是“不强制为0,而是控制其变小”;
- L2 不会像 L1 一样使参数归零,但会持续压缩大的权重;
- 这有助于模型在保持全部特征的情况下减少过拟合。
快速知识卡片(可打印记忆)
| 项 | L1 范数 | L2 范数 |
|---|---|---|
| 公式 | (\sum | x_i |
| 名称 | 曼哈顿距离 | 欧几里得距离 |
| 特点 | 稀疏、鲁棒 | 平滑、常用 |
| 正则化应用 | Lasso(特征选择) | Ridge(稳定优化) |
| 适用场景 | 高维稀疏建模 | 连续模型控制复杂度 |
| 损失函数 | MAE | MSE |
| 面试关键词 | 特征选择、正则稀疏性 | 权重控制、余弦相似度归一化 |
相关文章:
)
线性代数—向量与矩阵的范数(Norm)
参考链接: 范数(Norm)——定义、原理、分类、作用与应用 - 知乎 带你秒懂向量与矩阵的范数(Norm)_矩阵norm-CSDN博客 什么是范数(norm)?以及L1,L2范数的简单介绍_l1 norm-CSDN博客 范数(Norm…...

微服务基础-Ribbon
1. Ribbon简介: 客户端的负载均衡: 2....

移除生产环境所有console.log
大多数团队都会要求不能在生产环境输出业务侧的内容,但是往往业务开发人员会有疏漏,所以需要在工程化环境中,整体来管理console.log。我最近也是接到这样一个需求,整理了一下实现方案。 不同团队,不同场景,…...

数字人接大模型第二步:实时语音同步
接上例第一步,还是dh_live项目,增加了一个完整的实时对话样例,包含vad-asr-llm-tts-数字人全流程,以弥补之前的只有固定的问答的不足。 VAD(Voice Activity Detection,语音活动检测)VAD用于检测用户是否正在说话,从而触发后续的语音处理流程。 ASR(Automatic Speech R…...

Tomcat的安装与配置
Tomcat Tomcat是一个Java圈子中广泛使用的HTTP服务器. 后续学习Severlet内容,就是依赖Tomcat. Java程序员,要想写个网站出来,绕不开Tomcat. 我们这里使用Tomcat8 在bin目录下,这两个文件尤为重要,需要说明的是,Tomcat是那Java写的,所以在运行时需要jdk. bat后缀:是Window…...

Spring AI Alibaba - MCP连接 MySQL
先看效果 直接问他数据库有什么表。 大模型调用MySQL进行查询 搭建项目 添加依赖 创建项目后新添加Maven 依赖: <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web</artifactId> …...

Spring Cloud Stream喂饭级教程【搜集全网资料整理】
文章较长,建议收藏关注,随时查看 Spring Cloud Stream 简介 Spring Cloud Stream 是 Spring 提供的一个框架,用于构建与共享消息系统相连接的高度可伸缩的事件驱动微服务,它建立在 Spring 已有的成熟组件和最佳实践之上ÿ…...

prometheus手动添加k8s集群外的node-exporter监控
1、部署node-exporter 1)helm方式部署 rootiZj6c72dzbei17o2cuksmeZ:~# helm repo add prometheus-community https://prometheus-community.github.io/helm-charts "prometheus-community" has been added to your repositories rootiZj6c72dzbei17o2cu…...
中安装Docker)
Linux(Centos版本)中安装Docker
文章目录 Linux(Centos版本)中安装Docker整体流程 Linux(Centos版本)中安装Docker整体流程 进入root权限进行安装: 下面开始安装Docker: 1、安装docker的yum管理工具:记得将yum仓库更改为国内的镜像源&…...
)
C语言-- 深入理解指针(4)
C语言-- 深入理解指针(4) 一、回调函数二、冒泡排序三、qsort函数3.1 使用qsort函数排序整型数据3.2 使用qsort函数排序double数据3.3 使用qsort来排序结构体数据 四、模仿qsort库函数实现通用的冒泡排序4.1 通用冒泡排序函数排序整型数据4.2 通用冒泡排…...

牟乃夏《ArcGIS Engine地理信息系统开发教程》学习笔记3-地图基本操作与实战案例
目录 一、开发环境与框架搭建 二、地图数据加载与文档管理 1. 加载地图文档(MXD) 2. 动态添加数据源 三、地图浏览与交互操作 1. 基础导航功能 2. 书签管理 3. 量测功能 四、要素选择与属性查询 1. 属性查询 2. 空间查询 五、视图同步与鹰眼…...

Spark Streaming实时数据处理实战:从DStream基础到自定义数据源集成
park-Streaming概述 Spark-Streaming是什么 Spark Streaming 用于流式数据的处理。Spark Streaming 支持的数据输入源很多,例如:Kafka、Flume、Twitter等,以及和简单的 TCP 套接字等等。数据输入后可以用 Spark 的高度抽象原语如:…...

微软GraphRAG的安装和在RAG中的使用体会
文章目录 0. 简介(1)**技术原理**(2)**优势**(3)**开源与演进** 1. 下载graphrag.git2.安装 poetry3.初始化项目:建立cases目录4. 修改.env5.修改settings.yaml,将两处 api_base改成中转站地址:…...
的使用指南)
Python学习记录7——集合set()的使用指南
文章目录 引言一、集合特性二、创建方式三、元素操作1、添加元素(1)add(element)(2)update(iterables) 2、删除元素(1)remove(element)(2)discard(element)(3)…...

apkpure 谷歌插件 下载的apk包
谷歌插件市场搜索 apkpure 然后直接搜索下载就行了 想看apk包中的静态资源,直接改apk 为zip后缀解压就行了 apple的ipa包也是相同的道理...

Android四大核心组件
目录 一、为什么需要四大组件? 二、Activity:看得见的界面 核心功能 生命周期图解 代码示例 三、Service:看不见的劳动者 两大类型 生命周期对比 注意陷阱 四、BroadcastReceiver:消息传递专员 两种注册方式 广播类型 …...

WSL2里手动安装Docker 遇坑
在 WSL2 里手动安装 Docker Engine 时遇坑:systemctl 和 service 命令在默认的 WSL2 Ubuntu 中 无法使用,因为 WSL2 没有 systemd。怎么办? 自己操作让 Docker Engine(dockerd)直接跑起来,挂到 /var/run/do…...

【ROS2】ROS开发环境配置——vscode和git
古月21讲-ROS2/1.系统架构/1.5_ROS2开发环境配置/ ROS机器人开发肯定离不开代码编写,课程中会给大家提供大量示例源码,这些代码如何查看、编写、编译 安Linux中安装装git sudo apt install git下载教程源码 《ROS2入门21讲》课程源码的下载方式&#x…...

django.db.models.query_utils.DeferredAttribute object
在 Django 中,当你看到 django.db.models.query_utils.DeferredAttribute 对象时,通常是因为你在查询时使用了 only() 或 defer() 方法来延迟加载某些字段。这两个方法允许你控制数据库查询中的字段加载方式,从而优化查询性能。 only() 方法…...

Linux内核中的编译时安全防护:以网络协议栈控制块校验为例
引言:内存安全的无声守卫者 在操作系统内核开发中,内存溢出引发的错误往往具有极高的隐蔽性和破坏性。Linux内核作为承载全球数十亿设备的基石,其网络协议栈的设计尤其注重内存安全性。本文通过分析一段看似简单的内核代码,揭示Linux如何通过编译时静态检查(Compile-Time…...
)
第11章 安全网络架构和组件(一)
11.1 OSI 模型 协议可通过网络在计算机之间进行通信。 协议是一组规则和限制,用于定义数据如何通过网络介质(如双绞线、无线传输等)进行传输。 国际标准化组织(ISO)在20世纪70年代晚期开发了开放系统互连(OSI)参考模型。 11.1.1 OSI模型的…...

Git常用命令简明教程
本教程整合并优化了Git核心命令,涵盖初始化、配置、文件操作、分支管理、远程仓库操作及常见场景,适合快速入门和日常参考。命令按使用流程分组,简洁明了,包含注意事项和最佳实践。 1. 初始化与配置 初始化Git仓库并设置基本配置…...

在 Ubuntu 24.04 系统上安装和管理 Nginx
1、安装Nginx 在Ubuntu 24.04系统上安装Nginx,可以按照下面的步骤进行: 1.1、 更新系统软件包列表 在安装新软件之前,需要先更新系统的软件包列表,确保获取到最新的软件包信息。打开终端,执行以下命令: …...
)
数据结构——二叉树和堆(万字,最详细)
目录 1.树 1.1 树的概念与结构 1.2 树相关的术语 1.3 树的表示法 2.二叉树 2.1 概念与结构 2.2 特殊的二叉树 2.2.1 满二叉树 2.2.2 完全二叉树 2.3 二叉树存储结构 2.3.1 顺序结构 2.3.2 实现顺序结构二叉树 2.3.2.1 堆的概念与结构 2.3.2. 2 堆的插入与删除数据…...

IdeaVim 配置与使用指南
一、什么是 IdeaVim? IdeaVim 是 JetBrains 系列 IDE(如 IntelliJ IDEA, WebStorm, PyCharm 等)中的一个插件,让你在 IDE 里使用 Vim 的按键习惯,大大提升效率。 安装方法: 在 IDE 中打开 设置(Settings) →…...

前端浏览器窗口交互完全指南:从基础操作到高级控制
浏览器窗口交互是前端开发中构建复杂Web应用的核心能力,本文深入探讨23种关键交互技术,涵盖从传统API到最新的W3C提案,助您掌握跨窗口、跨标签页的完整控制方案。 一、基础窗口操作体系 1.1 窗口创建与控制 // 新窗口创建(现代浏…...

考研系列-计算机组成原理第五章、中央处理器
一、CPU的功能及结构 1.运算器的基本结构 2.控制器结构...

python+flask+flask-sockerio,部署后sockerio通信异常
前言 用python开发了一个flask web服务,前端用html,前后端通过socketio通信,开发环境,windowsminicondavscode,开发完成后本地运行没有问题,然后就开始部署,噩梦就开始了。 问题描述 程序是部…...

深度解析:TextRenderManager——Cocos Creator艺术字体渲染核心类
一、类概述 TextRenderManager 是 Cocos Creator 中实现动态艺术字体渲染的核心单例类。它通过整合资源加载、缓存管理、异步队列和自动布局等功能,支持普通字符模式和图集模式两种渲染方案,适用于游戏中的动态文本(如聊天内容、排行榜&…...

同样开源的自动化工作流工具n8n和Dify对比
n8n和Dify作为两大主流工具,分别专注于通用自动化和AI应用开发领域,选择哪个更“好用”需结合具体需求、团队能力及业务场景综合判断。以下是核心维度的对比分析: 一、核心定位与适用场景 维度n8nDify核心定位开源全场景自动化工具ÿ…...
完整讲解与实战应用)
设计模式每日硬核训练 Day 16:责任链模式(Chain of Responsibility Pattern)完整讲解与实战应用
🔄 回顾 Day 15:享元模式小结 在 Day 15 中,我们学习了享元模式(Flyweight Pattern): 通过共享对象,分离内部状态与外部状态,大量减少内存开销。适用于字符渲染、游戏场景、图标缓…...

基于边缘人工智能的AI无人机-更高效更安全的飞行任务执行
基于边缘人工智能的AI无人机-更高效更安全的飞行任务执行 人工智能有可能改变人们的生活和工作方式。人工智能和无人机是近年来发展迅速的两项技术。当这两种技术结合在一起时,它们会创造出许多以前不可能的应用。基于人工智能的无人机旨在独立执行任务,…...

30、不是说字符串是不可变的吗,string s=“abc“;s=“123“不就是变了吗?
一、核心概念澄清:不可变性的真实含义 1、不可变性的定义 字符串不可变性指对象内容不可修改,而非变量不可修改。 类比: 不可变字符串 装在密封信封里的信纸(内容不可更改)变量赋值 更换信封的指向(从…...

线上查询车辆出险记录:快速掌握事故情况!
在如今汽车成为人们日常不可或缺的交通工具之际,车辆出险记录成为了许多车主关注的焦点之一。为了帮助车主们快速了解车辆出险、理赔、事故记录,现在有了一种便捷的方式,那就是通过API接口在线查询。本文将介绍如何利用API接口,通…...

Python爬虫课程实验指导书
1.1Requests类库的认知 1.1.1 认识请求类库 Requests是用Python语言编写,基于,采用Apache2 Licensed开源协议的。它比urllib更加方便,可以节约我们大量的工作,完全满足HTTP测试需求。urllibHTTP库 Requests官网地址:ht…...

streamlit实现非原生的按钮触发效果 + flask实现带信息的按钮触发
目录 简介不携带信息的触发隐藏指定st.button(label, key)触发button的html代码汇总 携带信息的触发为什么需要携带信息前端JavaScript修改flask处理总代码 简介 由于streamlit可以同时在实现前后端结合,非常方便,但是这也造成了user难以方便的对页面的…...

机器学习基础——Seaborn使用
1.使用tips数据集,创建一个展示不同时间段(午餐/晚餐)账单总额分布的箱线图 import matplotlib.pyplot as plt import numpy as np import pandas as pd import seaborn as snstips pd.read_csv(./tips.csv)sns.boxplot(data tips,x time,y total_bill, )plt.show() 2.使用…...

Godot开发2D冒险游戏——第三节:游戏地图绘制
一、初步构建游戏地图 在游戏场景当中添加一个新的子节点:TileMapLayer 这一层称为瓦片地图层 根据提示,下一步显然是添加资源 为TileMapLayer节点添加一个TileSet 将地板添加进来,然后选择自动分割图集 自定义时要确保大小合适 让Godot自…...

Spark Mllib 机器学习
概述 机器学习是什么 根据百度百科的定义: 机器学习是一种通过算法和模型使计算机从数据中自动学习并进行预测或决策的技术。 定义比较抽象,根据常见的机器学习可以总结出三个关键字: 算法、经验、性能。 机器学习的过程可以抽象成一个pipel…...

在windows使用docker打包springboot项目镜像并上传到阿里云
1、前提:已有spring项目 2、在项目根目录下创建Dockerfile文件 FROM openjdk:11 WORKDIR /ruoyi-admin COPY ruoyi-admin/build/libs/lifecolor-web.jar lifecolor-web.jar CMD ["java", "-jar", "lifecolor-web.jar"] 3、选…...

前端高频面试题day3
JavaScript作用域理解 核心概念 作用域:定义变量/函数的可见范围及生命周期,分为 全局作用域、函数作用域、块级作用域。作用域链:变量查找从当前作用域逐级向上直至全局,遵循词法作用域(静态作用域)。闭…...

时空特征如何融合?LSTM+Resnet有奇效,SOTA方案预测准确率超91%
LSTM有着不错的时序信息提取能力,ResNet有着不错的空间特征信息提取能力。如果现在有时空特征融合的创新需求,我们是否能将LSTM和ResNet两者的优点融合起来呢? 随着这个思路下去,LSTM ResNet混合模型横空出世,在各个…...

蓝桥杯Java全攻略:从零到一掌握竞赛与企业开发实战
蓝桥杯Java软件开发竞赛已成为全国高校学生展示编程能力的重要舞台,本指南将带您从零开始构建完整的Java知识体系,不仅覆盖蓝桥杯高频考点,还延伸至企业级开发实战,助您在竞赛中脱颖而出并为未来职业发展奠定坚实基础。 一、Java基础语法与数据结构 竞赛解题流程图设计 蓝…...

【Nginx】负载均衡配置详解
Nginx作为高性能的HTTP服务器和反向代理服务器,提供了强大的负载均衡功能。本文将详细介绍Nginx负载均衡的配置方法和相关策略。 一、基础负载均衡配置 1.单服务示例配置 配置nginx.conf模块 在Nginx配置文件中定义upstream模块: worker_processes a…...

打造企业级AI文案助手:GPT-J+Flask全栈开发实战
一、智能文案革命的序幕:为什么需要AI文案助手? 在数字化营销时代,内容生产效率成为企业核心竞争力。据统计,营销人员平均每天需要撰写3.2篇文案,而传统人工创作存在三大痛点: 效率瓶颈:创意构…...

【文献速递】snoRNA-SNORD113-3/ADAR2通过对PHKA2的A-to-I编辑影响胶质母细胞瘤糖脂代谢
Cui等人于2025年在Cellular & Molecular Biology Letters上的发表一篇研究论文,题目为“Effect of SNORD113-3/ADAR2 on glycolipid metabolism in glioblastoma via A-to-I editing of PHKA2”。这篇文章的核心内容是研究胶质母细胞瘤(GBMÿ…...

视频HLS分片与关键帧优化深度解析
视频HLS分片与关键帧优化深度解析 🌐 HLS基础架构 #mermaid-svg-OQmrXfradiCv3EGC {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-OQmrXfradiCv3EGC .error-icon{fill:#552222;}#mermaid-svg-OQmrXfrad…...

再谈从视频中学习:从给视频打字幕的Humanoid-X、UH-1到首个人形VLA Humanoid-VLA:迈向整合第一人称视角的通用人形控制
前言 本博客内,之前写了比较多的大脑相关的,或者上肢操作,而解读运动控制、规划的虽也有,但相对少 故近期 准备多写写双足人形的运动控制相关 一方面,我们有些客户订单涉及这块二方面,想让双足人形干好活…...

Ubuntu下MySQL的安装
Ubuntu下MySQL的安装 1. 查看当前操作系统版本2. 添加MySQL APT源2.1 访问下载页面,并下载发布包2.2 执行安装指令2.3 安装MySQL 3. 查看MySQL状态4. 设置开机自启动 1. 查看当前操作系统版本 通过命令lsb_release -a查看: 2. 添加MySQL APT源 2.1 访问下…...

DataStreamAPI实践原理——快速上手
引入 通过编程模型,我们知道Flink的编程模型提供了多层级的抽象,越上层的API,其描述性和可阅读性越强,越下层API,其灵活度高、表达力越强,多数时候上层API能做到的事情,下层API也能做到&#x…...

