当前位置：首页 > news >正文

DS B/B+/B*树及其应用(21)

news 来源：原创 2025/7/2 2:46:37

文章目录

前言
一、常见的搜索结构
- 内查找
- 外查找
二、B树的概念
三、B树的插入分析
四、B树的插入实现
- B树的节点设计
- B树的查找
- B树插入Key / Key & Value的过程
- B树的完整插入代码
- B树的中序遍历
- B树的删除
- B树的性能分析
五、B+树
六、B*树
七、B树系列总结及其应用
总结

前言

我们计算机界有自己的3b1b！！！

附上链接：
B树(B-树) - 来由, 定义, 插入, 构建
B树(B-树) - 删除
数据结构合集 - B+树

这个真的是难死我了，还得是我，谢谢DeepSeek老师！

一、常见的搜索结构

内查找

种类	数据格式	时间复杂度
顺序查找	无要求	O(N)
二分查找	有序	O(logN)
二叉搜索树	无要求	O(N)
二叉平衡树(AVL树和红黑树)	无要求	O(logN)
哈希	无要求	O(1)

外查找

以上结构适合用于数据量相对不是很大，能够一次性存放在内存中，进行数据查找的场景。如果数据量很大，比如有100G数据，无法一次放进内存中，那就只能放在磁盘上了，如果放在磁盘上，有需要搜索某些数据，那么如何处理呢？那么我们可以考虑将存放关键字及其映射的数据的地址放到一个内存中的搜索树的节点中，找数据时比较关键字，找到关键字也就找到这个数据在磁盘的地址，然后去这个地址去磁盘访问数据。

在这里插入图片描述

节点可以不存关键字，只存对应磁盘的地址。这个时候查找就要拿着地址去访问磁盘然后看关键字是否匹配。这个时候还是一样关键字比当前节点关键字大往右走，否则往左走。每一次比较节点都是一次IO

但是这里的问题是，要走高度次磁盘IO，因为节点里面只有地址要进行关键字比较就要读一次磁盘。这个时候 AVL/红黑树就不适合了，都是O(logN)，虽然在内存中查找比较快，10亿个数字需要30次。但是在磁盘中如果是30次IO，那就很慢了。还有哈希表，虽然查找说是O(1)，但是这个O(1)并不是一次而是常数次，更大的问题是极端场景下哈希冲突可能会非常严重，效率会下降很多。即使哈希表挂的是红黑树还是O(logN)。

在这里插入图片描述
使用平衡二叉树搜索树的缺陷：

平衡二叉树搜索树的高度是logN，这个查找次数在内存中是很快的。但是当数据都在磁盘中时，访问磁盘速度很慢，在数据量很大时，logN次的磁盘访问，是一个难以接受的结果。

使用哈希表的缺陷：

哈希表的效率很高是O(1)，但是一些极端场景下某个位置冲突很多，导致访问次数剧增，也是难以接受的。

那有没有更好的数据结构能够替代上面的东西呢？

就是我们今天讲得内容，B树及其系列！！！

对于磁盘IO来说，其实我们是IO定位需要较长的时间，于是我们可以在此基础上去做文章

压缩高度，二叉变多叉
一个节点存有多个关键字及映射的值

二、B树的概念

1970年，R.Bayer和E.mccreight提出了一种适合外查找的树，它是一种平衡的多叉树，称为B树(后面有一个B的改进版本B+树，然后有些地方的B树写的的是B-树，注意不要误读成"B减树")。一棵m阶( m > 2 )的B树，是一棵平衡的M路平衡搜索树，可以是空树或者满足一下性质：

根节点至少有两个孩子
每个分支节点都包含k-1个关键字和k个孩子，其中 ceil(m/2) ≤ k ≤ m ceil是向上取整函数（分支节点，孩子比关键字保持多一个的关系）
每个叶子节点都包含k-1个关键字，其中 ceil(m/2) ≤ k ≤ m
所有的叶子节点都在同一层
每个节点中的关键字从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域划分
每个结点的结构为：（n，A0，K1，A1，K2，A2，… ，Kn，An）其中，Ki(1≤i≤n)为关键字，且Ki<Ki+1(1≤i≤n-1)。Ai(0≤i≤n)为指向子树根结点的指针。且Ai所指子树所有结点中的关键字均小于Ki+1。n为结点中关键字的个数，满足ceil(m/2)-1≤n≤m-1。

Ai是指向孩子的指针，Ki是关键字，从每个结点的结构上我们就可以看到孩子的数量比关键字多一个。

总结：
在这里插入图片描述
实际上M通常会设计的比较大，M = 1024，一个节点1023个关键字，1024个孩子。

三、B树的插入分析

最难的要来咯！

为了简单起见，假设M = 3. 即三叉树，正常来说每个节点中最多存储两个关键字，最少一个关键字，两个关键字可以将区间分割成三个部分，因此节点应该有三个孩子。

用序列 {53, 139, 75, 49, 145, 36, 101} 构建B树的过程如下：

根节点至少有两个孩子，这里可以这样理解，最开始插入一个关键字，它有两个孩子，可以认为是空。所以根节点要单独拿出来。

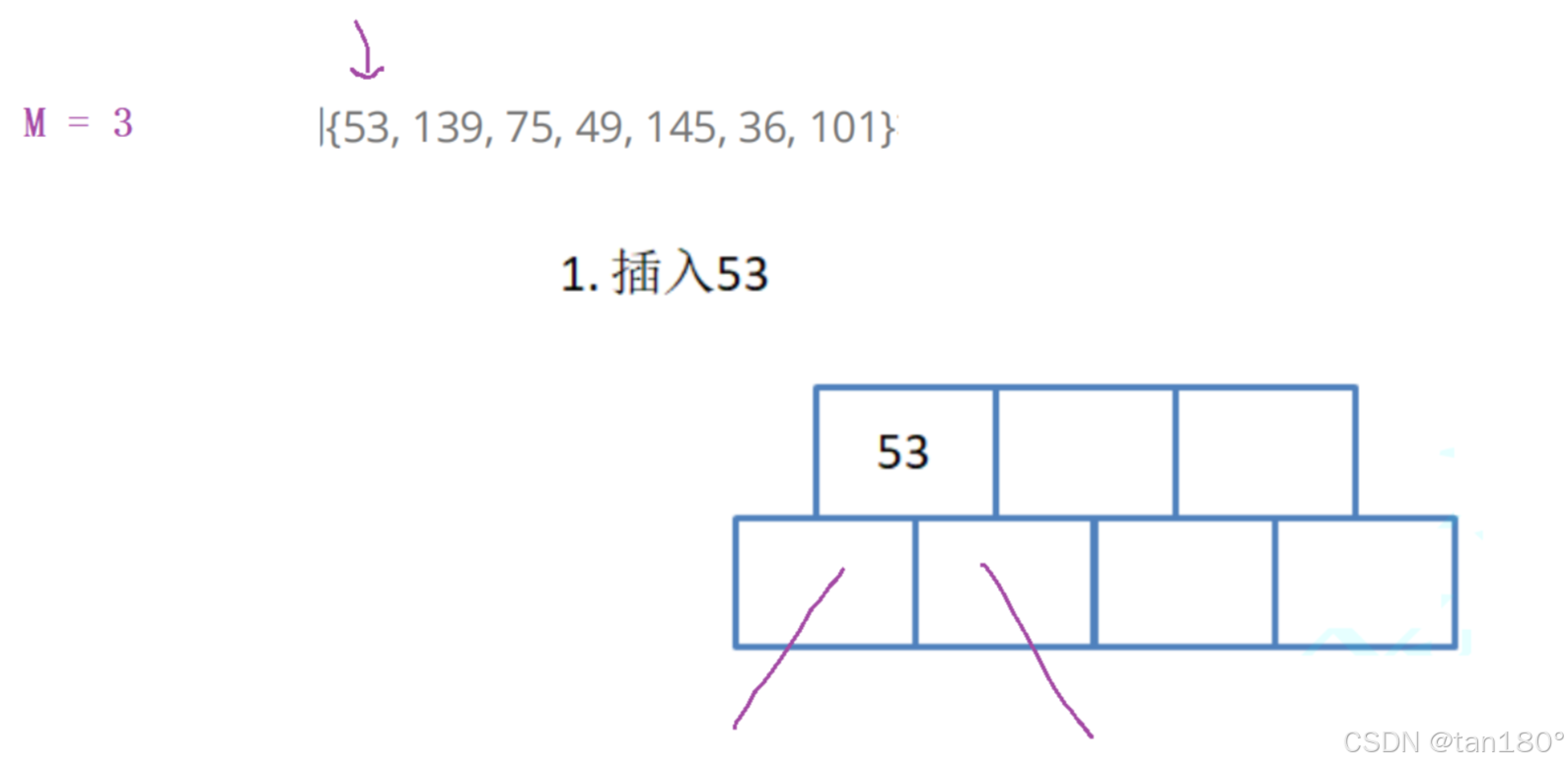
在这里插入图片描述
注意到 M = 3，正常来说不应该是2个关键字和3个孩子吗，为什么这里是3个关键字和4个孩子？多放一个是有原因的。

插入139没有什么影响

在这里插入图片描述
在插75，如果不多开一个，这个地方待会实现会变得复杂。插入的值因为要保证是有序的，所以可能在最前面，可能在中间，可能在最后面。但是现在并不敢就直接插入，一插入就要越界了。关键字个数等于M，关键字最多只能有M-1个。

在这里插入图片描述
基于这里的原因，我们就多给一个。

在这里插入图片描述
多给一个空间的好处是，方便插入，直接插入满了在分裂，不用管插在哪要挪动那些数据，也不怕越界。浪费一个空间不算啥。

在这里插入图片描述
关键字的数量等于M，则满了，满了就分裂出一个兄弟，提取中位数M/2，将中位数右边值和孩子拷贝给兄弟。将中位数给父亲，如果没有父亲就创建新的根。

插入49，注意新增节点只能在叶子节点插入。要保证节点内关键字是有序的，内部可以用直接插入排序挪动关键字和孩子。
在这里插入图片描述
插入145

插入36，发现关键字个数等于M，申请一个兄弟，找到中位数，将中位数右边的关键字和孩子分裂拷贝兄弟，提取中位数插入到父亲。插入要移动关键字和它的右孩子。插入之后别忘记最后要连接兄弟节点。

在这里插入图片描述
插入101，关键字等于M会分裂拷贝给兄弟，然后提取中位数给父亲，父亲插入之后，父亲的关键字也等于M了，也会分裂。分裂拷贝，找到中位数 M/2 ，申请兄弟节点，将中位数右边的关键字以及左孩子拷贝给兄弟，最后还要在将最后一个孩子也要拷贝给兄弟。然后提取中位数给父亲，父亲插入之后，如果父亲不满就结束，如果满就持续分裂。
在这里插入图片描述

B树的插入，你会发现它是天然平衡，因为它是向右和向上生长。

新插入的节点，一定是在叶子节点。因为叶子节点没有孩子，不影响关键字和孩子的关系。分支节点孩子保持比关键字多一个的关系。叶子节点满了，分裂出一个兄弟，提取中位数，向父亲插入一个值和孩子。

根节点分裂，增加一层。越到最后根节点越不容易分裂。

假设 M = 1024。一个节点最多放1023个关键字，1024个孩子，4层M路B树，就可以放一万亿个关键字和孩子了。
在这里插入图片描述
当然这是满的情况，不满我们也可以看一下，然后对比

插入过程总结：

如果树为空，直接插入新节点中，该节点为树的根节点
树非空，找待插入元素在树中的插入位置(注意：找到的插入节点位置一定在叶子节点中)
检测是否找到插入位置(假设树中的key唯一，即该元素已经存在时则不插入)
按照插入排序的思想将该元素插入到找到的节点中
检测该节点是否满足B-树的性质：即该节点中的元素个数是否等于M，如果小于则满足
如果插入后节点不满足B树的性质，需要对该节点进行分裂：
申请新节点
找到该节点的中间位置
将该节点中间位置右侧的元素以及其孩子搬移到新节点中
将中间位置元素以及新节点往该节点的双亲节点中插入，即继续4
如果向上已经分裂到根节点的位置，插入结束

四、B树的插入实现

B树的节点设计

template<class K, class V, size_t M>
struct BTreeNode
{// 孩子的数量比关键字的数量多一个/*pair<K, V>          _kvs[M - 1];BTreeNode<K, V, M>* _subs[M];*/// 空间一个空间，方便分裂，方便我们插入以后在分裂pair<K, V>          _kvs[M];BTreeNode<K, V, M>* _subs[M + 1];BTreeNode<K, V, M>* _parent;size_t _kvSize;BTreeNode():_kvSize(0),_parent(nullptr){for (size_t i = 0; i < M + 1; ++i){_subs[i] = nullptr;}}
};

B树的查找

比当前关键字小一定在它的左边，比它大就往右继续找，如果越界了，就往最后一个关键字的右孩子去找。走到叶子节点的nullptr说明没找到。

在这里插入图片描述

	// 第i个key的左孩子是subs[i]// 第i个key的右孩子是subs[i + 1]pair<Node*, int> Find(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){size_t i = 0;while (i < cur->_kvSize)				// 如果M比较大，这里应该改一改换成二分查找会快一些{if (cur->_kvs[i].first < key)		// key大于当前位置key，往右找++i;else if (cur->_kvs[i].first > key)	// key小于当前位置key，就往左孩子去找break;elsereturn make_pair(cur, i);}parent = cur;cur = cur->_subs[i];}// 没有找到return make_pair(parent, -1);}

B树插入Key / Key & Value的过程

按照直接插入排序的思想插入key，移动key也要移动它的右孩子，最后在把中位数和孩子插入

	// 往cur里面插入一个kv和subvoid InsertKV(Node* cur, const pair<K, V>& kv, Node* sub){// 将kv找到合适的位置插入进去int i = cur->_kvSize - 1;for (; i >= 0; ){if (cur->_kvs[i].first < kv.first){break;}else{// kv[i]往后挪动，kv[i]的右孩子也挪动cur->_kvs[i + 1] = cur->_kvs[i];cur->_subs[i + 2] = cur->_subs[i + 1];--i;}}cur->_kvs[i + 1] = kv;cur->_subs[i + 2] = sub;cur->_kvSize++;if (sub){sub->_parent = cur;}}

在这里插入图片描述

B树的完整插入代码

	bool Insert(const pair<K, V>& kv){// 初始处理// 处理空树情况if (_root == nullptr){_root = new Node;_root->_kvs[0] = kv;_root->_kvSize = 1;return true;}// 查找键是否存在// 返回一个pair，包含节点指针和键的索引(若找到)pair<Node*, int> ret = Find(kv.first);// 已经有了，不能插入  (当前如果允许插入就是mutil版本)if (ret.second >= 0){return false;}// 往cur节点中插入一个newkv和sub// 1、如果cur没满就结束// 2、如果满了就分裂，分裂出兄弟以后，往父亲插入一个关键字和孩子，再满还要继续分裂// 3、最坏的情况就是分裂到根，原来根分裂，产生出一个新的根，就结束了// 也就是说，我们最多分裂高度次Node* cur = ret.first;pair<K, V> newkv = kv;Node* sub = nullptr;while (1){InsertKV(cur, newkv, sub); // 1、如果cur没满就结束if (cur->_kvSize < M){return true;}else // 2、满了，需要分裂{// 分裂出一个兄弟节点Node* newnode = new Node;// 1、拷贝右半区间给分裂的兄弟节点int mid = M / 2;int j = 0;int i = mid + 1;newkv = cur->_kvs[mid];cur->_kvs[mid] = pair<K, V>();for (; i < M; ++i){newnode->_kvs[j] = cur->_kvs[i];cur->_kvs[i] = pair<K, V>();newnode->_subs[j] = cur->_subs[i];cur->_subs[i] = nullptr;if (newnode->_subs[j]){newnode->_subs[j]->_parent = newnode;}j++;newnode->_kvSize++;}// 还剩最后一个右孩子// 指针比键多一个，所以最后一个右孩子需要单独处理newnode->_subs[j] = cur->_subs[i];if (newnode->_subs[j]){newnode->_subs[j]->_parent = newnode;}cur->_kvSize = cur->_kvSize - newnode->_kvSize - 1;// 1、如果cur没有父亲，那么cur就是根，产生新的根// 2、如果cur有父亲，那么就要转换成往cur的父亲中插入一个key和一个孩子newnodeif (cur->_parent == nullptr){_root = new Node;_root->_kvs[0] = newkv;_root->_subs[0] = cur;_root->_subs[1] = newnode;cur->_parent = _root;newnode->_parent = _root;_root->_kvSize = 1;return true;}else{// 往父亲去插入newkv和newnode，转换成迭代逻辑sub = newnode;cur = cur->_parent;}}}return true;}

B树的中序遍历

	void InOrder(){_InOrder(_root);}void _InOrder(Node* cur){if (cur == nullptr){return;}size_t i = 0;while (i < cur->_kvSize){// 先访问左子树，再访问当前值_InOrder(cur->_subs[i]);cout << cur->_kvs[i].first << " ";++i;}// 再访问最后一个右子树_InOrder(cur->_subs[i]);}

在这里插入图片描述

B树的删除

这里就不细说了，大家可自行看开篇的视频，如果说插入要防上溢出，这里就要防止下溢出

B树的性能分析

B树上搜索一个值时间复杂度最坏就是走高度次假设每层结点关键字都是满的设为M，孩子也是M。忽略掉孩子比关键字多1。

设有h层，一层一层下去这就是一个等比数列。

在这里插入图片描述
这里我们可以用错位相减法来算

不满的情况

可以看出B树的效率是很高的！

五、B+树

B树总体来说还是非常依赖于搜索树，还区分左孩子右孩子。并且分支节点孩子的数量比关键字多一个，整体而言反而让结构变得复杂了不少。基于一系列原因大佬又对B树进行了优化。

B+树是B树的变形，是在B树基础上优化的多路平衡搜索树，B+树的规则跟B树基本类似，但是又在B树的基础上做了以下几点改进优化：

分支节点的子树指针与关键字个数相同
分支节点的子树指针p[i]指向关键字值大小在[k[i]，k[i+1])区间之间
所有叶子节点增加一个链接指针链接在一起
所有关键字及其映射数据都在叶子节点出现
方便了去遍历，不需要从根开始了
所有关键字及其映射数据都在叶子节点出现

1也就是说孩子与关键字个数相等， 2也就是说B树以前下标和我相等是我的左孩子，现在在[k[i]，k[i+1])之间。1、2合在一起相当于取消了最左边的那个子树。

在这里插入图片描述
分支节点根叶子节点有重复的值，分支节点存的是叶子节点索引。
父亲中存的是孩子节点中的最小值做索引。

在这里插入图片描述

比如在这颗B+树搜索一个33，是如何搜索的呢？
先找到根，如果比5还小根本不存在，5已经是最小的了。

在这里插入图片描述
如果比5大，往下一个。比28大还往下一个。比65小说明在65的左边。去P2找

比28大往下一个，比35小说明在55的左边。去P1找。最终找到33。如果是34，最终就是去33的右孩子去找，但33右孩子是空，所以找不到
在这里插入图片描述
插入的过程也是类似的。这里简单了解一下 M == 3 B+树分裂过程，它这里的结构搞的简单一些

刚开始插入要两层节点，一层做分支，一层做根
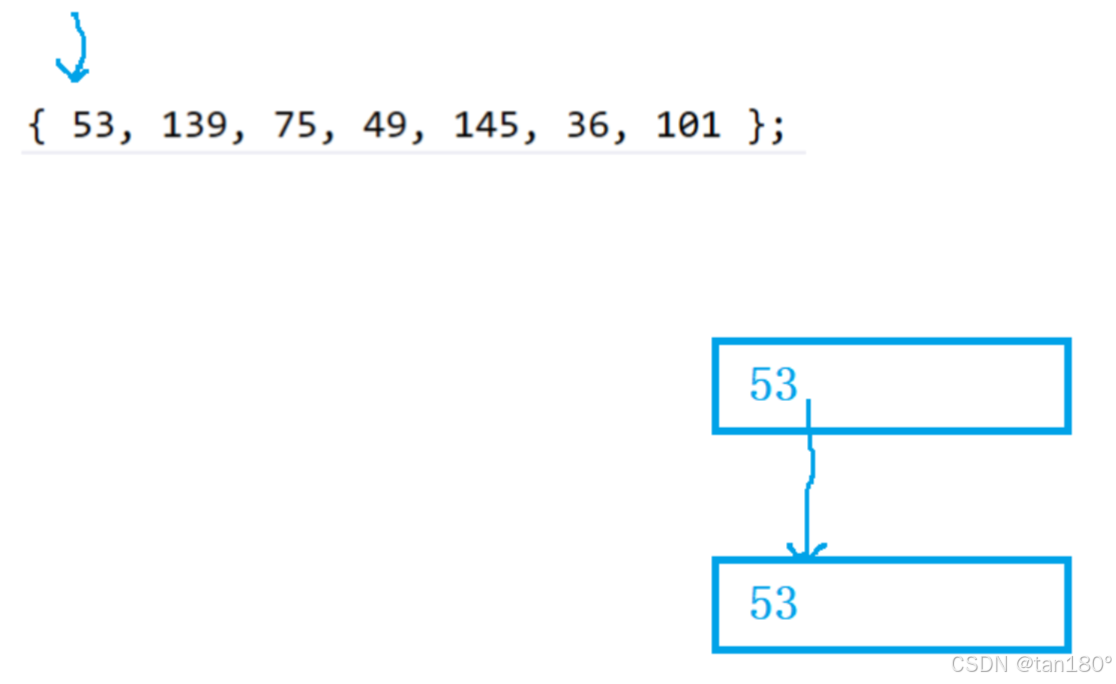
在这里插入图片描述
插入到139。目前关键字是3个了。因为B+树分支节点孩子和关键字个数相同所以不用分裂。只有当关键字个数 > M 才分裂

插入 49，关键字个数 > M 分裂
插入满了之后分裂一半给兄弟，转换成往父亲插入一个key和一个孩子，孩子就是兄弟，key就是兄弟的第一个最小值的key。
在这里插入图片描述
插入145，36

插入101，第二次分裂

再来两个数150、155，我们看看连续分裂的情况
在这里插入图片描述
B+树的插入过程根B树基本是类型的，细节区别在于，第一次插入两层节点，一层做分支，一层做根。后面一样往叶子去插入，插入满了之后分裂一半给兄弟，转换成往父亲插入一个key和一个孩子，孩子就是兄弟，key就是兄弟的第一个最小值的key。

总结：

简化B树孩子比关键字多一个的规则，变成相等
所有值都在叶子节点，方便遍历查找所有值

六、B*树

在B+树的分支节点增加指向兄弟节点的指针。
B+树节点原来关键字个数最少是1/2M，B*树要求节点关键字最少是2/3M，最多是M

在这里插入图片描述
B+树的分裂：

当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针

B*树最大的改变就是让每个节点更满。因为B树和B+树都有一个缺陷，可能会浪费一半的空间

B*树的结点关键字和孩子数量 -> [2/3M，M]

B*树的分裂：

当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针。

在这里插入图片描述

所以，B*树分配新结点的概率比B+树要低，空间使用率更高

七、B树系列总结及其应用

B树：有序数组+平衡多叉树；
B+树：有序数组链表+平衡多叉树；
B*树：一棵更丰满的，空间利用率更高的B+树

B树最常见的应用就是用来做索引。索引通俗的说就是为了方便用户快速找到所寻之物，比如：书籍目录可以让读者快速找到相关信息，hao123网页导航网站，为了让用户能够快速的找到有价值的分类网站，本质上就是互联网页面中的索引结构

当数据量很大时，为了能够方便管理数据，提高数据查询的效率，一般都会选择将数据保存到数据库，因此数据库不仅仅是帮助用户管理数据，而且数据库系统还维护着满足特定查找算法的数据结构，这些数据结构以某种方式引用数据，这样就可以在这些数据结构上实现高级查找算法，该数据结构就是索引

数据库有一个 Cathes&Buffers ，意思是数据存在磁盘中直接访问太慢，所以建一个缓存(可以考虑使用LRU)。对于B+树而言可以把所有分支节点存储到Cache里，搜索必然要走分支。如果使用B树缓存就没有多大意义，因为太大了（B树的分支节点存 key & value），分支节点既有数据也要数据所在磁盘的地址。B+树相比于B树而言，分支节点只存key，分支节点比较小。分支节点映射的磁盘数据块就可以尽量加载Cache。

总结

难死我了这个，大家一定要好好理解！！！

文章目录

前言

一、常见的搜索结构

内查找

外查找

二、B树的概念

三、B树的插入分析

四、B树的插入实现

B树的节点设计

B树的查找

B树插入Key / Key & Value的过程

B树的完整插入代码

B树的中序遍历

B树的删除

B树的性能分析

五、B+树

六、B*树

七、B树系列总结及其应用

总结

相关文章：