当前位置：首页 > news >正文

【C++指南】哈希驱动的封装：如何让unordered_map/set飞得更快更稳？【上】

news 来源：原创 2025/8/17 15:09:53

🌟 各位看官好，我是egoist2023！

🌍 种一棵树最好是十年前，其次是现在！

💬 注意：本文在哈希函数中主讲除法散列法，乘法散列法、全域散列法、双重散列等自行了解。

🚀 今天来学习哈希表的相关知识，为之后unordered_map/set的封装打下基础。

👍 如果觉得这篇文章有帮助，欢迎您一键三连，分享给更多人哦

引入：直接定址法

在现实生活中，我们往往会将一类东西跟另一种东西进行绑定，且这种 关系具有一定的联系 。

在计算机当中也是必然，如“left”的中文意思是“左边”，“string”的中文意思是“字符串”等等。而对于每个数字都有对应存储的下标。

当 关键字的范围⽐较集中 时，⽐如⼀组关键字都在[0,99]之间，那么我们开⼀个100个数的数组，每个关键字的值直接就是存储位置的下标。

但是如果 一组关键字比较分散 ，如只出现了1、20、99时，此时要开100空间的数组有97个空间会被浪费，这显然不是我们期望的。因此，关于一段 哈希的故事就此展开 。

哈希

哈希(hash)又称散列，是⼀种组织数据的⽅式。从译名来看，有散乱排列的意思。本质就是通过哈希函数把关键字Key跟存储位置建⽴⼀个映射关系，查找时通过这个哈希函数计算出Key存储的位置，进⾏快速查找。

哈希函数

⼀个好的哈希函数应该让N个关键字被等概率的均匀的散列分布到哈希表的M个空间中，但是实际中却很难做到。因此我们要尽量往这个⽅向去考量设计。

除法散列法（除留余数法）

当数据比较分散的情况下，用直接定址法是无法很好地处理问题的，那是否能仅用较小地空间让保证所有的值都映射到该空间上来呢(保证空间大于值数量)？于是有人提出了除法散列法的概念并对此进行了说明。

除法散列法也叫做除留余数法，假设哈希表的大小为M，那么通过key除以M的余数作为映射位置的下标，也就是哈希函数为：h(key) = key % M。（这样即能保证所有的值都在这个空间上）

哈希冲突和负载因子

当使⽤除法散列法时，要 尽量避免M为某些值 ，如2的幂，10的幂等。

如果是，那么key %2 ^X 本质相当于保留key的后X位，那么后x位相同的值，计算出的哈希值都是⼀样的，就冲突了。如：{63 , 31}看起来没有关联的值，如果M是16，即2^4，保留后4位，因为63的⼆进制后8位是 00111111，31的⼆进制后8位是 00011111，后四位都是相同的，那么都会映射到同一个空间上去，这样就产生了冲突，即哈希冲突。

因此 当使⽤除法散列法时，建议M取不太接近2的整数次幂的⼀个质数(素数) 。

负载因子：

假设哈希表中已经映射存储了N个值，哈希表的⼤⼩为M，M一定要大于，那么负载因子 = N/M，保证负载因子小于1。
负载因⼦越⼤，说明M是接近于N的，则空间利⽤率越⾼，相对地哈希冲突的概率越⾼；

负载因⼦越⼩，说明M的空间很大，则空间利用率低，相对地哈希冲突的概率越低。

处理哈希冲突

实践中哈希表⼀般还是选择除法散列法作为哈希函数，当然哈希表 ⽆论选择什么哈希函数也避免不了冲突 ，那么插⼊数据时，如何解决冲突呢？主要有两种两种⽅法，开放定址法和链地址法。

开放定址法

在开放定址法中所有的元素都放到哈希表⾥，当⼀个关键字key⽤哈希函数计算出的位置冲突了，则按照某种规则找到⼀个没有存储数据的位置进⾏存储，开放定址法中负载因⼦⼀定是⼩于的。这⾥的规则有三种： 线性探测、⼆次探测、双重探测（自行了解） 。（哈希表有三种状态表示： 存在、空、删除 ）

开放定址法的哈希表结构

enum Status
{EMPTY,EXIST,DELETE
};template<class K, class V>
struct HashData
{pair<K, V> _kv;Status _status = EMPTY;
};template<class K, class V, class Hash = HashFunc<K>>
class HashTable
{
public:HashTable(size_t size = 11):_tables(size), _n(0){}//...private:vector<HashData<K, V>> _tables;size_t _n;
};

优化

但是上面的实现并不是那么好，如果当映射的元素_n/_tables.size()大于负载因子时，显然是需要扩容的，如果选择2倍扩容，原本的11空间变为22空间，看似没有毛病。但前面我们说过，使用除法散列法时，要尽量避免M为某些值，即取不太接近2的整数次幂的⼀个质数。因此，不能直接地选择2倍扩容地方式来放大空间。那代码又该如何实现呢？

提前造好一些数据，这些数据得保证是质数，且是不太接近2的整数次幂的⼀个质数；
每次扩容的时候都往我们造好的数据上进行扩容。

static const int __stl_num_primes = 28;
static const unsigned long __stl_prime_list[__stl_num_primes] =
{53,         97,         193,       389,       769,1543,       3079,       6151,      12289,     24593,49157,      98317,      196613,    393241,    786433,1572869,    3145739,    6291469,   12582917,  25165843,50331653,   100663319,  201326611, 402653189, 805306457,1610612741, 3221225473, 4294967291
};inline unsigned long __stl_next_prime(unsigned long n)
{const unsigned long* first = __stl_prime_list;const unsigned long* last = __stl_prime_list + __stl_num_primes;const unsigned long* pos = lower_bound(first, last, n);return pos == last ? *(last - 1) : *pos;
}enum Status
{EMPTY,EXIST,DELETE
};template<class K, class V>
struct HashData
{pair<K, V> _kv;Status _status = EMPTY;
};template<class K, class V, class Hash = HashFunc<K>>
class HashTable
{
public:HashTable(size_t size = __stl_num_primes):_tables(size), _n(0){}//...private:vector<HashData<K, V>> _tables;size_t _n;
};

在上面这段程序中，哈希表默认初始空间是28，当大于负载因子时进行扩容，第一次扩容是53，第二次是97…… ，可以发现，每次扩容都是以近乎2倍扩容且满足不太接近2的整数次幂的⼀个质数。这种手动造数据的方法看似笨拙，实则这难道不是利用其特性下的一种取巧吗？

线性探测

在映射数据的时候可能会存在哈希冲突，此时从发⽣冲突的位置开始，依次线性向后探测，直到寻找到下⼀个没有存储数据的位置为⽌，如果⾛到哈希表尾，则回绕到哈希表头的位置。

h(key) = hash0 = key % M，hash0位置冲突了，则线性探测公式为：hc(key,i) = hashi = (hash0 + i) % M， i = {1, 2, 3, ..., M − 1}，保证线性探测时能从队尾走到队头，且因为负载因⼦小于1，则最多探测M-1次，⼀定能找到⼀个存储key的位置。

可以发现线性探测的问题会占用其他值可能映射到的空间，会导致原本不冲突的值产生哈希冲突。严重的话肯呢个会使多个hash0，hash1，hash2，hash3的值都争夺hash3位置，这种现象叫做群集/堆积。

二次探测（了解）

存在哈希冲突是必然的，但有什么比较好的方法可以减少哈希冲突的现象呢？

从发⽣冲突的位置开始，依次左右按⼆次⽅跳跃式探测，直到寻找到下⼀个没有存储数据的位置为止，如果往右⾛到哈希表尾，则回绕到哈希表头的位置；如果往左⾛到哈希表头，则回绕到哈希表尾的位置；

h(key) = hash0 = key % M , hash0位置冲突了，则⼆次探测公式为：hc(key,i) = hashi = (hash0 ± i^2 ) % M， i = {1, 2, 3, ...,M/2 }；
⼆次探测当 hashi = (hash0 − i 2 )%M 时，当hashi<0时，需要hashi += M。

线性探测实现

bool Insert(const pair<K, V>& kv)
{size_t hash0 = kv.first % _tables.size();size_t hashi = hash0;size_t i = 1;//如果该点存在 --> 线性探测while (_tables[hashi]._status == EXIST){hashi = (hashi + i) % _tables.size();i++;}_tables[hash0]._kv = kv;_tables[hash0]._status = EXIST;++_n;return true;
}

扩容

方案一：新建一个哈希表，遍历旧表让里面的数据重新映射到新表当中；

方案二：采用复用的手段将旧表数据映射到新表中。

if ((double)_n / (double)_tables.size() > 0.7)
{HashTable<K, V, Hash> newHT(__stl_next_prime(_tables.size() + 1));for (size_t i = 0;i < _tables.size();i++){if (_tables[i]._status == EXIST){newHT.Insert(_tables[i]._kv);}}_tables.swap(newHT._tables);
}

查找和删除

查找规律：巧妙利用线性探测的特性

删除规律：采用Find函数寻找该值是否存在，如果存在标记为del，返回true；否则，返回false。

	HashData<K, V>* Find(const K& key){size_t hash0 = key % _tables.size();size_t hash1 = hash0;size_t i = 1;while (_tables[hash1]._status != EMPTY){if (_tables[hash1]._kv.first == key && _tables[hash1]._status != DELETE){return &_tables[hash1];}hash1 = (hash1 + i) % _tables.size();++i;}return nullptr;}bool Erase(const K& key){HashData<K, V>* ret = Find(key);if (ret){ret->_status = DELETE;return true;}else{return false;}}

代码实现

static const int __stl_num_primes = 28;
static const unsigned long __stl_prime_list[__stl_num_primes] =
{53,         97,         193,       389,       769,1543,       3079,       6151,      12289,     24593,49157,      98317,      196613,    393241,    786433,1572869,    3145739,    6291469,   12582917,  25165843,50331653,   100663319,  201326611, 402653189, 805306457,1610612741, 3221225473, 4294967291
};inline unsigned long __stl_next_prime(unsigned long n)
{const unsigned long* first = __stl_prime_list;const unsigned long* last = __stl_prime_list + __stl_num_primes;const unsigned long* pos = lower_bound(first, last, n);return pos == last ? *(last - 1) : *pos;
}enum Status
{EMPTY,EXIST,DELETE
};template<class K, class V>
struct HashData
{pair<K, V> _kv;Status _status = EMPTY;
};template<class K>
struct HashFunc
{size_t operator()(const K& key){return (size_t)key;}
};template<class K, class V, class Hash = HashFunc<K>>
class HashTable
{
public:HashTable(size_t size = __stl_num_primes):_tables(size), _n(0){}bool Insert(const pair<K, V>& kv){//扩容 --> 负载因子大于0.7if ((double)_n / (double)_tables.size() > 0.7){HashTable<K, V, Hash> newHT(__stl_next_prime(_tables.size() + 1));for (size_t i = 0;i < _tables.size();i++){if (_tables[i]._status == EXIST){newHT.Insert(_tables[i]._kv);}}_tables.swap(newHT._tables);}size_t hash0 = kv.first % _tables.size();size_t hashi = hash0;size_t i = 1;//如果该点存在 --> 线性探测while (_tables[hashi]._status == EXIST){hashi = (hashi + i) % _tables.size();i++;}_tables[hash0]._kv = kv;_tables[hash0]._status = EXIST;++_n;return true;}HashData<K, V>* Find(const K& key){size_t hash0 = key % _tables.size();size_t hash1 = hash0;size_t i = 1;while (_tables[hash1]._status != EMPTY){if (_tables[hash1]._kv.first == key && _tables[hash1]._status != DELETE){return &_tables[hash1];}hash1 = (hash1 + i) % _tables.size();++i;}return nullptr;}bool Erase(const K& key){HashData<K, V>* ret = Find(key);if (ret){ret->_status = DELETE;return true;}else{return false;}}private:vector<HashData<K, V>> _tables;size_t _n;
};

链地址法

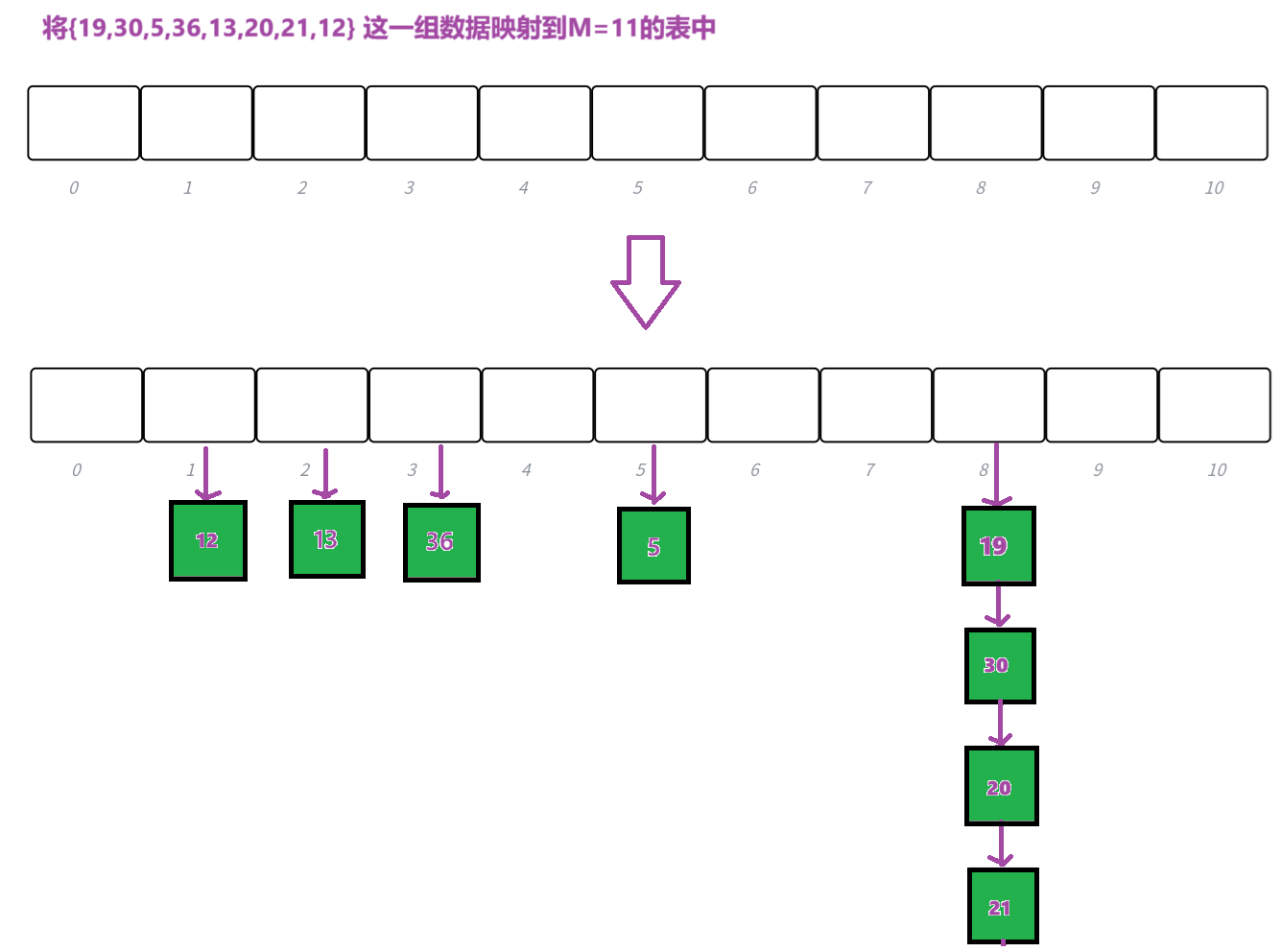
开放定址法无论怎样势必会造成哈希冲突，因其占⽤的都是哈希表中的空间，始终存在互相影响问题。那如何解决这种弊端呢？

链地址法为了解决这种冲突，不是再将所有的数据直接存储在哈希表中，而是通过指针的方式让每一个值都映射到对应空间，即使产生冲突会用指针的方式将它们悬挂起来，挂在哈希表该位置下面，当然我们形象地称这种方法为拉链法或哈希桶。

但是在一些极端场景下，如有人恶意造出一段数据让它都映射到同一个位置，导致某个桶特别长，查询时间复杂度达到了O(N)。有大佬提出，如果这个桶的长度超过⼀定阀值(8)时就把链表转换成红⿊树。（用全域散列法也可）

链地址法的结构实现

    //手动造数据见上面template<class K,class V>struct HashNode{pair<K, V> _kv;HashNode<K, V>* _next;HashNode(const pair<K, V>& kv):_next(nullptr),_kv(kv){}};template<class K, class V>class HashTable{typedef HashNode<K, V> Node;public:HashTable(size_t size = __stl_next_prime(0)):_tables(size, nullptr),_n(0){}private:vector<Node*> _tables;size_t _n;};

特殊情况：插入元素不是数字

如果插入元素是浮点数、负数情况呢？

仿函数的作用再次体现出来了，无论是整数、浮点数、负数，统一强转成正数来处理，找到该映射的位置，对查找、删除等操作都不会受到影响，因为我们同样需要将目标值强制转成正数映射到对应位置。

	//仿函数template<class K>struct HashFunc{size_t operator()(const K& key){return (size_t)key; // --> 针对浮点、负数等情况}};

针对字符串

但是字符串的处理，并不能直接强转成正数来处理，这并不被允许。因此，在这里采用特化的思想进行特殊处理，实现如下。

	//针对字符串template<>struct HashFunc<string>{size_t operator()(const string& key){size_t hash0 = 0;for (auto& ch : key){//对不同字符串但hash0相同的处理，减少冲突hash0 *= 131;hash0 += ch;}return hash0;}};

改动

template<class K, class V, class Hash = HashFunc<K>>

扩容

开放定址法负载因⼦必须⼩于1，链地址法的负载因⼦就没有限制了。在stl中的实现最⼤负载因⼦基本控制在1，⼤于1就扩容，我们同样采用此逻辑进行扩容。

扩容操作时，开一个新的哈希表，需要将旧表上的值都重新映射到新表中。

方法一：由于是链地址法的实现，一个位置下可能会挂着多个值（即哈希桶），那么就需要遍历该位置中桶的每个结点，将每个结点的值重新映射到新表中，而每次操作都需要申请新结点，并把旧表中该结点释放掉。显然，这种方式是非常浪费的，且效率非常低效。
方法二：正是由于采用的是链地址法的实现，由于哈希表中每个位置都是一个指针，那么我们只需要遍历旧表中结点映射在新表中的位置，使其指向旧表中该结点。最后，将旧表置为空，交换新旧链表，完成扩容操作。

		bool Insert(const pair<K, V>& kv){//不允许冗余if (Find(kv.first))return false;Hash hs;//需要扩容if (_n == _tables.size()){// 也可以，但是扩容新开辟节点，释放旧节点，有点浪费/*HashTable<K, V> newHT(__stl_next_prime(_tables.size() + 1));for (size_t i = 0; i < _tables.size(); i++){Node* cur = _tables[i];while (cur){newHT.Insert(cur->_kv);cur = cur->_next;}}_tables.swap(newHT._tables);*/vector<Node*> newtables(__stl_next_prime(_tables.size() + 1), nullptr);//遍历旧表for (size_t i = 0;i < _tables.size();i++){Node* cur = _tables[i];while (cur){//将旧表的每个结点插在新表中Node* next = cur->_next;size_t hash0 = hs(cur->_kv.first) % newtables.size();cur->_next = newtables[hash0];newtables[hash0] = cur;cur = next;}_tables[i] = nullptr;}_tables.swap(newtables);}size_t hash0 = hs(kv.first) % _tables.size();Node* newnode = new Node(kv);//头插newnode->_next = _tables[hash0];_tables[hash0] = newnode;++_n;return true;}

删除

        bool Erase(const K& key){Hash hs;size_t hash0 = hs(key) % _tables.size();Node* prev = nullptr;Node* cur = _tables[hash0];while (cur){if (cur->_kv.first == key){if (prev == nullptr){_tables[hash0] = cur->_next;}else{prev->_next = cur->_next;}--_n;delete cur;return true;}prev = cur;cur = cur->_next;}return false;}

代码实现

	static const int __stl_num_primes = 28;static const unsigned long __stl_prime_list[__stl_num_primes] ={53,         97,         193,       389,       769,1543,       3079,       6151,      12289,     24593,49157,      98317,      196613,    393241,    786433,1572869,    3145739,    6291469,   12582917,  25165843,50331653,   100663319,  201326611, 402653189, 805306457,1610612741, 3221225473, 4294967291};inline unsigned long __stl_next_prime(unsigned long n){const unsigned long* first = __stl_prime_list;const unsigned long* last = __stl_prime_list + __stl_num_primes;const unsigned long* pos = lower_bound(first, last, n);return pos == last ? *(last - 1) : *pos;}template<class K,class V>struct HashNode{pair<K, V> _kv;HashNode<K, V>* _next;HashNode(const pair<K, V>& kv):_next(nullptr),_kv(kv){}};//仿函数template<class K>struct HashFunc{size_t operator()(const K& key){return (size_t)key; // --> 针对浮点、负数等情况}};//针对字符串template<>struct HashFunc<string>{size_t operator()(const string& key){size_t hash0 = 0;for (auto& ch : key){//对不同字符串但hash0相同的处理，减少冲突hash0 *= 131;hash0 += ch;}return hash0;}};template<class K, class V, class Hash = HashFunc<K>>class HashTable{typedef HashNode<K, V> Node;public:HashTable(size_t size = __stl_next_prime(0)):_tables(size, nullptr),_n(0){}bool Insert(const pair<K, V>& kv){//不允许冗余if (Find(kv.first))return false;Hash hs;//需要扩容if (_n == _tables.size()){// 也可以，但是扩容新开辟节点，释放旧节点，有点浪费/*HashTable<K, V> newHT(__stl_next_prime(_tables.size() + 1));for (size_t i = 0; i < _tables.size(); i++){Node* cur = _tables[i];while (cur){newHT.Insert(cur->_kv);cur = cur->_next;}}_tables.swap(newHT._tables);*/vector<Node*> newtables(__stl_next_prime(_tables.size() + 1), nullptr);//遍历旧表for (size_t i = 0;i < _tables.size();i++){Node* cur = _tables[i];while (cur){//将旧表的每个结点插在新表中Node* next = cur->_next;size_t hash0 = hs(cur->_kv.first) % newtables.size();cur->_next = newtables[hash0];newtables[hash0] = cur;cur = next;}_tables[i] = nullptr;}_tables.swap(newtables);}size_t hash0 = hs(kv.first) % _tables.size();Node* newnode = new Node(kv);//头插newnode->_next = _tables[hash0];_tables[hash0] = newnode;++_n;return true;}Node* Find(const K& key){Hash hs;size_t hashi = hs(key) % _tables.size();Node* cur = _tables[hashi];while (cur){if (cur->_kv.first == key)return cur;cur = cur->_next;}return nullptr;}bool Erase(const K& key){Hash hs;size_t hash0 = hs(key) % _tables.size();Node* prev = nullptr;Node* cur = _tables[hash0];while (cur){if (cur->_kv.first == key){if (prev == nullptr){_tables[hash0] = cur->_next;}else{prev->_next = cur->_next;}--_n;delete cur;return true;}prev = cur;cur = cur->_next;}return false;}~HashTable(){for (size_t i = 0;i < _tables.size();i++){Node* cur = _tables[i];while (cur){Node* next = cur->_next;delete cur;cur = next;}_tables[i] = nullptr;}}private:vector<Node*> _tables;size_t _n;};

【C++指南】哈希驱动的封装：如何让unordered_map/set飞得更快更稳？【上】

🌟 各位看官好，我是egoist2023！ 🌍 种一棵树最好是十年前，其次是现在！ 💬 注意：本文在哈希函数中主讲除法散列法，乘法散列法、全域散列法、双重散列等自行了解。 &#x…...

编程日记 2025/8/17 15:09:53

论坛测试报告

作者前言 🎂 ✨✨✨✨✨✨🍧🍧🍧🍧🍧🍧🍧🎂 🎂 作者介绍： 🎂🎂 🎂 🎉🎉&#x1f389…...

编程日记 2025/8/9 21:48:23

人脸扫描黑科技：多相机人脸扫描设备，打造你的专属数字分身

随着科技的迅猛发展，人脸扫描这个词已经并不陌生，通过人脸扫描设备制作超写实人脸可以为影视制作打造逼真角色、提升游戏沉浸感，还能助力教育机构等领域生产数字人以丰富教学资源，还在安防、身份识别等领域发挥关键作用&#xff0…...

编程日记 2025/8/17 15:08:06

统计字符串每个字符出现频率

输入一个字符串，统计每个字符的出现频率，然后判断最大频率与最小频率的差值 cnt： 如果 cnt 是质数，则输出 "Lucky Word" 和差值； 否则输出 "No Answer" 和 0。 #include <bits/stdc.h> u…...

编程日记 2025/8/14 21:38:23

SQL-子查询

SQL子查询是嵌套在另一个SQL查询中的SELECT语句，将内部查询的结果作为外部查询的条件或者数据源。核心概念子查询是一个完整的SELECT语句，可以嵌入到其他查询的where, from, SELECT, HAVING等子句中，用于动态生成条件或临时数据集。例如…...

编程日记 2025/8/17 15:07:01

Python（21）Python日期时间完全指南：从基础到实战注意事项

目录一、背景与核心价值二、核心模块详解与实战2.1 datetime模块四剑客2.2 时区处理黄金法则三、企业级应用案例3.1 全球日志分析系统3.2 金融交易时间校验四、六大核心注意事项1. 时区意识优先原则‌2. 时间戳的精度陷阱‌3. 夏令时转换三步骤4. 日期格式化安全指南‌5. 性…...

编程日记 2025/8/12 4:54:19

【医学影像 AI】早产儿视网膜病变国际分类（第三版）

【医学影像 AI】早产儿视网膜病变国际分类（第三版） 0. 论文简介0.1 基本信息0.2 摘要0.3 缩略语0.4 ICROP3的关键内容总结 1. 引言2. 血管化位置：区域（ZONE）3. 加重病变与前加重病变4. 急性病变分期（阶段1-…...

编程日记 2025/8/17 15:09:52

焊接机器人的设计

一、引言随着制造业的发展，焊接工艺在各个领域得到广泛应用。焊接机器人具有焊接质量高、效率高、劳动强度低等优点，能够满足现代制造业对焊接生产的要求。设计一款性能优良的焊接机器人，对于提高焊接生产的自动化水平和产品质量具有重要意…...

编程日记 2025/8/17 8:34:07

SQL SERVER里面也可以插入存储过程,操作TCP,WEBSOCKET吗?数据发生改变时用于通知客户端

SQL SERVER里面也可以插入存储过程,操作TCP,WEBSOCKET吗?数据发生改变时用于通知客户端SQL存储过程入门🔥 - 人生得E不早朝深度思考完成用时28秒好的，用户的问题是：SQL Server里面是否可以通过插入存储过程来操作TCP或WebSocket&…...

编程日记 2025/8/17 15:07:48

利用 DeepSeek-R1 模型和计算机视觉微调模型实现马铃薯叶片疾病识别和分类

一、需求背景在农业现代化进程中，作物健康监测对于保障粮食安全和提高农业生产效率起着举足轻重的作用。马铃薯作为全球重要的粮食作物之一，其种植面积广泛，产量和质量直接关系到众多农户的生计以及食品供应链的稳定。准确、快速地鉴别马铃…...

编程日记 2025/8/16 22:11:02

文章记单词 | 第39篇（六级）

一，单词释义 themselves [əmˈselvz] pron. 他们自己；她们自己；它们自己；（用以加强语气）他们亲自，她们亲自，它们亲自；（反身代词） 指某人或某物本…...

编程日记 2025/8/17 15:06:59

深入理解C++中string的深浅拷贝

目录一、引言二、浅拷贝与深拷贝的基本概念 2.1 浅拷贝 2.2 深拷贝在C 中， string 类的深浅拷贝有着重要的区别。浅拷贝深拷贝 string 类中的其他构造函数及操作 resize 构造构造（赋值构造） 构造（拼接构造&#xf…...

编程日记 2025/8/17 15:07:50

C++ 常用的智能指针

C 智能指针一、智能指针类型概览 C 标准库提供以下智能指针（需包含头文件 <memory>）： unique_ptr：独占所有权，不可复制， 可移动shared_ptr：共享所有权，用于引用计数weak_pt…...

编程日记 2025/8/17 15:07:01

【AI部署】腾讯云GPU-常见故障—SadTalker的AI数字人视频—未来之窗超算中心 tb-lightly

ERROR: Could not find a version that satisfies the requirement tb-nightly (from torchreid) (from versions: none) ERROR: No matching distribution found for tb-nightly 解决阿里云 python -m pip install tb-nightly -i https://mirrors.aliyun.com/pypi/simple …...

编程日记 2025/8/16 22:41:23

三大等待和三大切换

三大等待 1、三大等待：等待的方式有三种：强制等待，隐性等待，显性等待。 1、强制等待：time.sleep(2)，秒优点：使用简单缺点：等待时间把握不准，容易造成时间浪费或者等待时…...

编程日记 2025/8/17 15:09:04

工程化实践：Flutter项目结构与规范

工程化实践：Flutter项目结构与规范在Flutter项目开发中，良好的工程化实践对于提高开发效率、保证代码质量和团队协作至关重要。本文将从项目结构、代码规范、CI/CD流程搭建以及包管理等方面，详细介绍Flutter项目的工程化最佳实践。项目结…...

编程日记 2025/8/17 15:08:06

数据结构-Map和Set

文章目录 1. 搜索树2. Map3. Set4. 哈希表4.1 哈希表的基本概念4.2 哈希表的实现方法4.3 Java中的哈希表实现 5. 哈希桶哈希桶的实现方式哈希桶的作用哈希桶的应用模拟实现 1. 搜索树二叉搜索树（Binary Search Tree, BST）是一种特殊的二叉树&#xff0…...

编程日记 2025/8/17 15:07:47

cpolar 内网穿透实现公网可以访问本机

1、登录网站，升级成专业版，测试的话建议选一个月付费，选择预留 2、保留的TCP地址增加一条记录，描述可以自己取 3、验证，生成一个Authtocken码 4、在安装目录下，打开CMD命令，复制上面的码运行aut…...

编程日记 2025/8/17 15:06:59

QT调用ffmpeg库实现视频录制

可以通过QProcess调用ffmpeg命令行，也可以直接调用ffmpeg库，方便。调用库安装ffmpeg ffmpeg -version 没装就装 sudo apt-get update sudo apt-get install ffmpeg sudo apt-get install ffmpeg libavdevice-dev .pro引入库路径，引入库 LIBS += -L/usr/lib/aarch64-l…...

编程日记 2025/8/15 2:32:53

AI专题（一）----NLP2SQL探索以及解决方案

前面写了很多编码、算法、底层计算机原理等相关的技术专题，由于工作方向调整的缘故，今天开始切入AI人工智能相关介绍。本来按照规划，应该先从大模型的原理开始介绍会比较合适，但是计划赶不上变化，前面通用大模型的工作…...

编程日记 2025/8/17 11:28:58

Redis 的指令执行方式：Pipeline、事务与 Lua 脚本的对比

Pipeline 客户端将多条命令打包发送，服务器顺序执行并一次性返回所有结果。可以减少网络往返延迟（RTT）以提升吞吐量。需要注意的是，Pipeline 中的命令按顺序执行，但中间可能被其他客户端的命令打断。典型场景&…...

编程日记 2025/8/16 11:52:29

群辉默认docker数据存储路径

做一下笔记今天不小心路径规划错误，好不容易找到了数据，特此做个路径记录。 /var/packages/ContainerManager/var/docker/...

编程日记 2025/8/17 15:09:06

【C++】入门基础【上】

目录一、C的发展历史二、C学习书籍推荐三、C的第一个程序1、命名空间namespace2、命名空间的使用3、头文件<iostream>是干什么的？ 个人主页<—请点击 C专栏<—请点击一、C的发展历史 C的起源可以追溯到1979年，当时Bjarne Stroustrup(本…...

编程日记 2025/8/17 15:09:06

Git LFS 学习笔记：原理、配置、实践与心路历程

最近在学习 Git LFS，把一些零散的笔记整理成一篇博文，记录我的学习思路与心路历程。以下内容均为个人理解总结，部分尚未在生产项目中验证，仅供回顾与参考。 🔍 Git LFS 是什么？原理是什么？ 刚接…...

编程日记 2025/8/10 5:34:25

SpringBoot集成oshi 查询系统数据

实现功能： <dependency><groupId>com.github.oshi</groupId><artifactId>oshi-core</artifactId><version>6.6.1</version></dependency><dependency><groupI…...

编程日记 2025/8/17 15:09:53

iOS Facebook 登录

iOS Facebook 登录官方文档 SDK下载链接...

编程日记 2025/8/17 15:08:04

uniapp打包IOS私钥证书过期了，如何在非mac系统操作

在非Mac系统下解决uniapp打包iOS私钥证书过期的问题，需通过以下步骤实现： --- ### **一、重新生成iOS证书（非Mac环境操作）** 1. **生成私钥和CSR文件** 使用OpenSSL工具（需提前安装）生成私钥和证书签…...

编程日记 2025/8/15 7:48:03

Axios的使用

Axios 是一个基于 Promise 的现代化 HTTP 客户端库，专为浏览器和 Node.js 设计。在企业级应用中，它凭借以下核心优势成为首选方案： 一、Axios 的核心优势特性说明Promise 支持天然支持异步编程，避免回调地狱拦截器机制可全局拦截…...

编程日记 2025/8/17 15:09:07

第八篇：系统分析师第三遍——3、4章

目录一、目标二、计划三、完成情况四、意外之喜(最少2点)1.计划内的明确认知和思想的提升标志2.计划外的具体事情提升内容和标志五、总结一、目标通过参加考试，训练学习能力，而非单纯以拿证为目的。 1.在复习过程中，训练快速阅读能力、掌…...

编程日记 2025/8/17 15:07:49

【2025-泛计算机类-保研/考研经验帖征集】

【2025-泛计算机类-保研/考研经验帖征集】打扰您1分钟时间看下这里： 这是一个无偿为爱发电的项目，旨在收集湖南大学2025届毕业的计算机类学科同学的经验帖， 我将定期汇总链接，在校内推免群中宣传，为校内的学弟学妹们…...

编程日记 2025/8/17 15:07:51

Flink介绍——实时计算核心论文之Kafka论文详解

引入我们通过S4和Storm论文的以下文章，已经对S4和Storm有了不错的认识： S4论文详解S4论文总结Storm论文详解Storm论文总结不过，在讲解这两篇论文的时候，我们其实没有去搞清楚对应的流式数据是从哪里来的。虽然S4里有Keyless …...

编程日记 2025/8/16 18:39:38

细节:如何制作高质量的VR全景图

细节：如何制作高质量的VR全景图 VR全景图是通过虚拟现实和3D技术实现的全景展示方式，能够将实景以1:1的比例等比复刻，并还原到互联网上，使用户能够在线上游览世界，获得沉浸式的体验。制作高质量的VR全景图是一个复杂而…...

编程日记 2025/8/17 15:08:04

深度学习中的概念——元素积（哈达玛积）

元素积操作（哈达玛积） 🔢 基本定义矩阵的哈达玛积对于两个同维度的矩阵： A [ a i j ] , B [ b i j ] A [a_{ij}], \quad B [b_{ij}] A[aij],B[bij] 它们的哈达玛积定义为： C A ∘ B 其中 c i j a i j…...

编程日记 2025/8/17 15:07:52

探索 Flowable 后端表达式：简化流程自动化

什么是后端表达式？ 在 Flowable 中，后端表达式是一种强大的工具，用于在流程、案例或决策表执行期间动态获取或设置变量。它还能实现自定义逻辑，或将复杂逻辑委托…… 后端表达式在 Flowable 的后端运行，无法访问前端…...

编程日记 2025/8/16 21:56:18

AI语音助手 React 组件使用js-audio-recorder实现，将获取到的语音转成base64发送给后端，后端接口返回文本内容

页面效果： js代码： import React, { useState, useRef, useEffect } from react; import { Layout, List, Input, Button, Avatar, Space, Typography, message } from antd; import { SendOutlined, UserOutlined, RobotOutlined, AudioOutlined, Stop…...

编程日记 2025/8/15 19:24:52

《软件设计师》复习笔记（11.6）——系统转换、系统维护、系统评价

目录一、遗留系统（Legacy System） 定义： 特点： 演化策略（基于价值与技术评估）： 高水平 - 低价值： 高水平 - 高价值： 低水平 - 低价值： 低水平 - 高价…...

编程日记 2025/8/17 5:47:38

学习threejs，使用EffectComposer后期处理组合器（采用RenderPass、GlitchPass渲染通道）

👨‍⚕️ 主页： gis分享者 👨‍⚕️ 感谢各位大佬点赞👍 收藏⭐ 留言📝 加关注✅! 👨‍⚕️ 收录于专栏：threejs gis工程师文章目录一、🍀前言1.1 ☘️THREE.EffectComposer 后期…...

编程日记 2025/8/16 9:34:36

Yarn的定义？

YARN（Yet Another Resource Negotiator） 是 Apache Hadoop 的核心组件之一，负责集群的资源管理和任务调度。它的主要作用是将 Hadoop 的资源管理和作业调度/监控功能分离，形成一个通用的资源管理平台，可以支持多种计算…...

编程日记 2025/8/14 5:46:36

职坐标IT培训热门技术实战精讲

在数字化转型浪潮中，人工智能、大数据与云原生已成为驱动产业升级的核心引擎。职坐标IT培训课程以实战导向为基石，聚焦高薪岗位核心技术栈，通过拆解企业级项目案例，将复杂的技术理论转化为可落地的工程实践。课程模块涵盖从架构设…...

编程日记 2025/8/11 23:18:32

前端：uniapp框架中＜scroll-view＞r如何控制元素进行局部滚动

以下是使用 <scroll-view> 实现局部滚动的完整示例，包含动态内容、滚动控制和滚动位置监听： 一、基础局部滚动示例 <template><view class"container"><scroll-view scroll-y :scroll…...

编程日记 2025/8/12 12:43:44

【KWDB 创作者计划】_算法篇---Stockwell变换

文章目录前言一、Stockwell变换原理详解1.1 连续S变换定义1.2 离散S变换1.3简介二、S变换的核心特点2.1频率自适应的时频分辨率2.1.1高频区域2.1.2低频区域 2.2无交叉项干扰2.3完全可逆2.4相位保持2.5与傅里叶谱的直接关系三、应用领域3.1地震信号分析3.2生物医学信号处理3.…...

编程日记 2025/8/14 18:10:29

桌面级OTA测试解决方案：赋能智能网联汽车高效升级

一、前言随着智能网联汽车的快速发展，OTA（Over-The-Air）技术已成为汽车软件更新和功能迭代的关键手段。为确保OTA升级的可靠性、安全性和效率，构建一套高效、便捷的桌面级OTA测试解决方案至关重要。本方案基于Vector先进的软硬…...

编程日记 2025/8/15 2:33:22

京东物流基于Flink StarRocks的湖仓建设实践

摘要：本文整理自京东物流高级数据开发工程师梁宝彬先生在 Flink Forward Asia 2024 论坛中的分享。内容主要为以下四个部分： 1、实时湖仓探索与建设 2、实时湖仓应用 3、问题与思考 4、未来展望今天，将分享的主题大纲包括：首先&a…...

编程日记 2025/8/17 14:22:24

【Test Test】灰度化和二值化处理图像

文章目录 1. 图像灰度化处理对比2. 代码示例3. 二值化处理 1. 图像灰度化处理对比 2. 代码示例 #include <opencv2/opencv.hpp> using namespace cv;int main() {Mat currentImage imread("path_to_image.jpg"); // 读取彩色图像Mat grayImage;// 将彩色图像…...

编程日记 2025/8/14 4:55:15

Docker快速入门

1 基本信息 1.1 基础概览 （1）容器与镜像容器‌：轻量级的独立运行时环境，基于Linux的命名空间（namespace）和控制组（cgroup）技术实现资源隔离‌。容器通过镜像创建，每个容…...

编程日记 2025/8/5 1:10:25

AI 编程工具—如何在 Cursor 中集成使用 MCP工具

AI 编程工具—如何在 Cursor 中集成使用 MCP工具这里我们给出了常用的MCP 聚合工具，也就是我们可以在这些网站找MCP服务这是一个MCP Server共享平台，用户可以在上面发布和下载MCP Server配置。在这里可以选择你需要的MCP 服务。如果你不知道你的mcp 对应的server 名称也不…...

编程日记 2025/8/13 12:10:08

航电系统通信与数据链技术分析

一、技术要点 1. 高带宽与低时延通信技术航电系统需支持实时数据传输，如民航VDL2数据链采用D8PSK调制和Reed Solomon编码技术，传输速率达31.5Kb/s，并通过物理层优化减少码间串扰。新一代LDACS系统则利用L频段频谱，提供比传统VD…...

编程日记 2025/8/16 15:35:48

windwos脚本 | 基于scrcpy，只投声音、只投画面

安装scrcpy，scrcpy自带adb 写脚本命名为 .bat 结尾注意这里的set "PATHD:\tools\scrcpy-win64-v3.2;%PATH%" 替换成scrcpy的安装目录 echo off :: 设置UTF-8编码 chcp 65001 > nul :: 设置标题 title 手机投屏工具:: 添加 scrcpy 路径到 PATH set &q…...

编程日记 2025/8/12 7:57:49

产品经理面试题与参考答案资料(2025年版）

一、技术背景与工具能力问题1：软件开发生命周期（SDLC）包括哪些阶段？作为产品经理，你如何参与每个阶段？参考答案：软件开发生命周期通常划分为需求分析、设计、开发、测试、部署和维护六个阶段。作为产品经理，你需要在...

编程日记 2025/7/25 11:10:37

HTML 初识

段落标签 <p>Lorem ipsum dolor sit amet consectetur adipisicing elit. Fugiat, voluptate iure. Obcaecati explicabo sint ipsum impedit! Dolorum omnis voluptas sint unde sed, ipsa molestiae quo sapiente quos et ad reprehenderit.&l…...

编程日记 2025/8/15 16:57:06

引入 ：直接定址法

哈希

哈希函数

除法散列法（除留余数法）

哈希冲突和负载因子

处理哈希冲突

开放定址法

优化

线性探测

二次探测（了解）

扩容

查找和删除

代码实现

链地址法

特殊情况：插入元素不是数字

改动

扩容

删除

代码实现

相关文章：

引入：直接定址法