当前位置：首页 > news >正文

数据结构——八大排序算法

news 来源：原创 2025/8/21 14:31:46

排序在生活中应用很多，对数据排序有按成绩，商品价格，评论数量等标准来排序。

数据结构中有八大排序，插入、选择、快速、归并四类排序。

插入排序

直接插入排序

希尔排序

选择排序

堆排序

冒泡排序

快速排序

hoare版本快排

挖坑法

前后指针法

归并排序

插入排序

什么是插入排序呢？插入排序就是把一个待排的值插入到已经有序的序列中，直到所有待排的值全部插入到序列中，得到一个新的有序序列。

插入排序有直接插入和希尔排序

直接插入排序

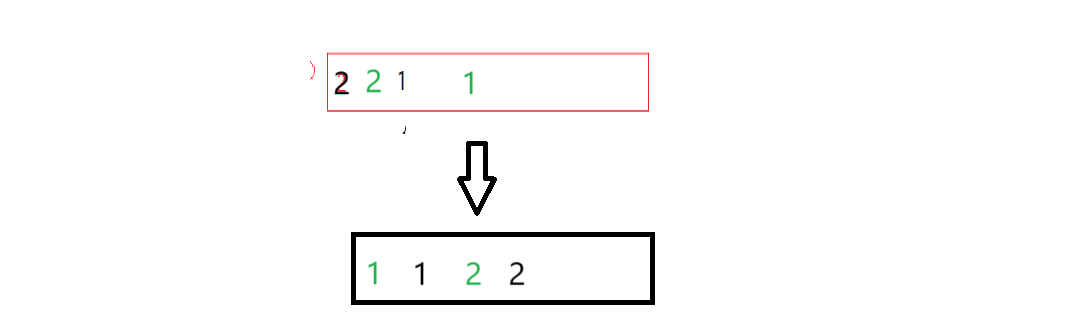
当插入到 i 个数据时，前i个数据已经有序，排第i个数据需要与前 i 个数据依次比较，将第 i 个数据放到合适的位置，根据下面的动图可以帮助更好的理解

代码实现：

void InsertSort(int* a, int n)
{for (int i = 1; i < n; i++){int end = i-1;int tmp = a[i];while (end >= 0){if (tmp < a[end]){a[end+1] = a[end];end -= 1;}else{break;}}a[end+1] = tmp;}
}

tmp来存储需要排序的值，end为需要排序值的前一个位置，tmp从后往前依次比较，当tmp小于end位置的值，就将这个值往后挪动，end往前移动一步，直到tmp大于或者end不满足进入循环的条件就把end+1下标的值改为tmp，就把前i个数据排好序了。

时间复杂度：最好情况：O(N) （数据全部有序）

平均情况：O(N^2)

最坏情况：O(N^2)（数据与我们要排的顺序逆序）

空间复杂度：O(1)

稳定性：稳定（判断稳定性的方法，在这组数据中有两个相同的数据，在把这组数据排好序后，在未排好时在后的数据不会在排好序后跑到未排好时在前的数据的前面）

在插入排序中如果有两个数据相同，在排序过程中，相同不会挪动该数据。

希尔排序

相比与直接插入排序希尔排序多了一个预排序，因为在直接插入排序中，这组数据越有序效率就越快，所以在希尔排序中就先对这组数据预排序，再使用直接插入排序。

那么怎么样进行预排序呢？如下

上图是gap=3的单趟排序。

距离为gap的为一组，按以上数据就可以分为三组，就这三组排序就可以达到预排序的效果，gap越大就分的组就越多，当gap=1时就是直接插入排序，所以我们可以先让gap为一个比较大的值，为数据个数的二分之一，一直减小直到为1，就排好序了。

代码展示：

void ShellSort(int* a, int n)
{int gap = n;while (gap>1){gap = gap / 2;//gap == 1 就是插入排序//gap > 1 预排序for (int j = 0; j < gap; j++){for (int i = gap + j; i < n; i += gap){int end = i - gap;int tmp = a[i];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}}
}

为什么这样效率会更快呢？，gap = 2^2^2^2^2……2^2,循环次数为logN，内循环为N，所以希尔排序的时间复杂度为NlogN（底为2）。

时间复杂度：最好情况：O(N^1.3)

平均情况：O(NlogN~N^2)

最坏情况：O(N^2)

空间复杂度：O(1)

稳定性：不稳定（因为在预排序时可能会把两个相同的数的相对前后位置改变）

选择排序

选择排序思想：每次选择待排序数据中最小（最大）的数据，存放在待排序列起始位置，直到全部数据排完。

代码实现：

void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void SelectSort(int* a, int n)
{int left = 0, right = n - 1;while (left < right){int maxi = left, mini = left;for (int i = left + 1; i <= right; i++){if (a[i] < a[mini]){mini = i;}if (a[i] > a[maxi]){maxi = i;}}Swap(&a[left], &a[mini]);if (left == maxi || right == mini){maxi = mini;}Swap(&a[right], &a[maxi]);left++;right--;}
}

这里我们思想是和选择一样的，只不过我们使用双指针从待排序列的两边开始，在序列中找最大和最小值，最小值放到待排的序列起始位置，最大的值放到待排序列的最后一个位置，当两个指针相等时就结束循环，这里需要注意的是在最小值交换到待排序列的位置时，left为待排序列的起始位置，right为最后一个位置，当left等于最大值的下标或者right等于最小值的下标时，需要将最小值的下标给最大值的下标。例如排序3、2、1、0。

这里进行了第一次交换，如果没有判断的话直接进入第二次交换就回到第一次交换之前，这两个数据就没有发生变换，导致排序失败。

时间复杂度：最好情况：O(N^2)

平均情况：O(N^2)

最坏情况：O(N^2)

空间复杂度：O(1)

稳定性：不稳定

示例：

堆排序

堆排序是利用堆积树来这种数据结构所设计的一种算法，通过堆来选数据，排升序要建大堆（每一个子树都满足双亲大于两个孩子），排降序建小堆（每一个子树都满足双亲小于两个孩子）。

在我之前的文章有堆更详细的讲解，更好帮住理解堆排序：https://blog.csdn.net/lrhhappy/article/details/147029631?spm=1001.2014.3001.5502

代码展示：

void AdjustDwon(int* a, int n, int parent)
{int child = parent * 2 + 1;while ((parent*2+1) < n){if ((child + 1) < n && a[child] < a[child + 1]){child++;}if (a[parent] < a[child]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapSort(int* a, int n)
{//建堆for (int i = (n-2)/2; i>=0; i--){AdjustDwon(a, n, i);}printArr(a, n);int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDwon(a, end, 0);end--;}printArr(a, n);
}

时间复杂度：最好情况：O(NlongN)

平均情况：O(NlongN)

最坏情况：O(NlongN)

空间复杂度：O(1)

稳定性：不稳定（想想示例）

冒泡排序

冒泡排序在是在初学是最早接触的排序，但是实际应用不怎么用，相比其他排序效率太低了。

冒泡思想：将键值较大的记录向序列的尾部移动，键值较小的记录向序列的前部移动。每次从序列起始位置开始与下一个位置比较，如果该位置大于下一个位置的值，就进行交换，就把最大的值换到序列的最后一个，循环往复，就可以排完全部数据。

代码展示：

//冒泡排序
void BubbleSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){for (int j = 0; j <n-i-1; j++){if (a[j] > a[j + 1]){Swap(&a[j], &a[j + 1]);}}}
}

时间复杂度：O(n^2) （不管要排序的序列是否有序，都需要进行比较）

空间复杂度：O(1)

稳定性：稳定（相等不会交换）

快速排序

hoare版本快排

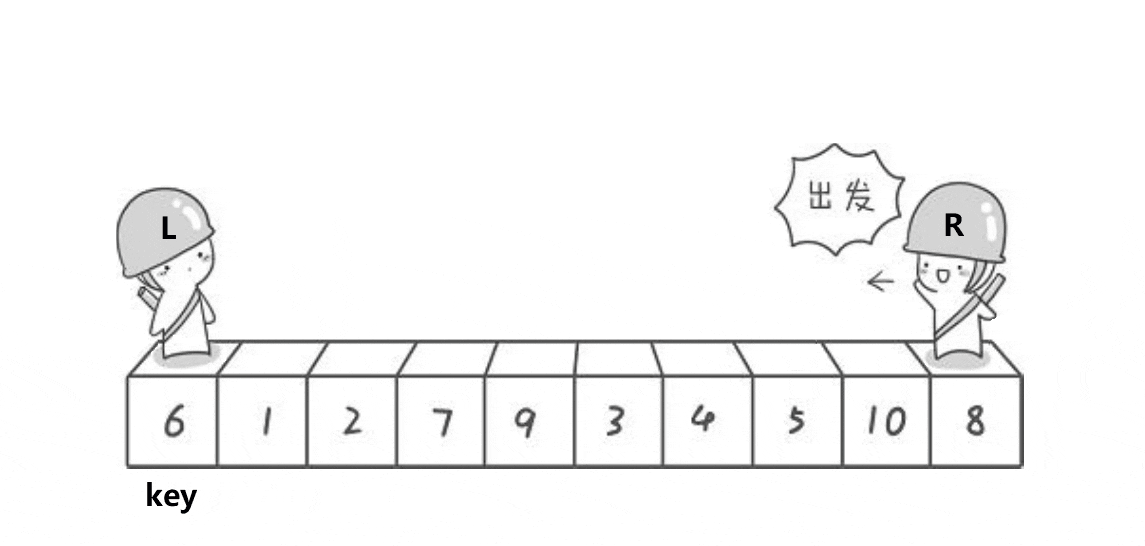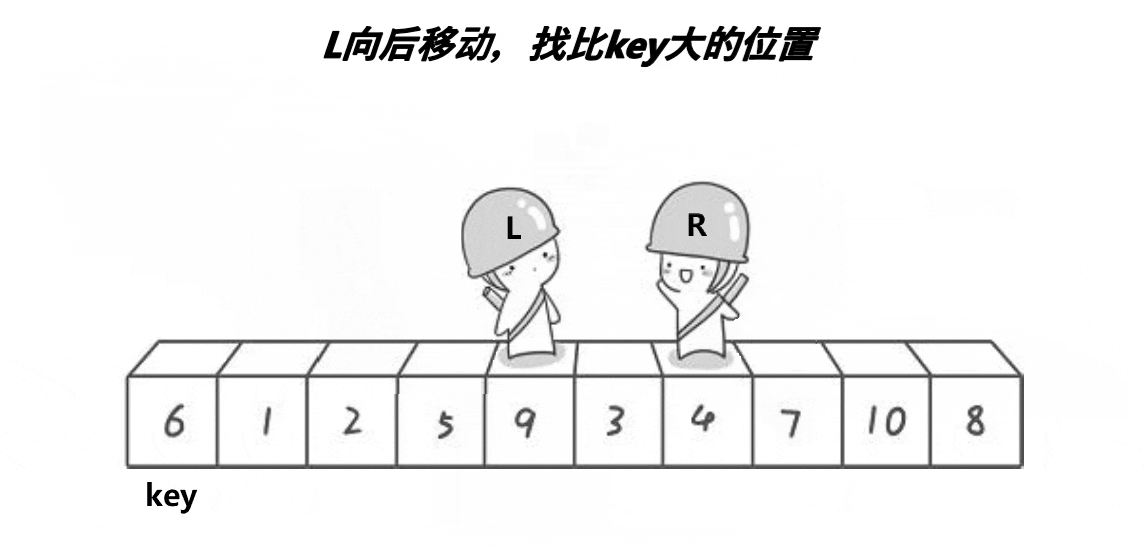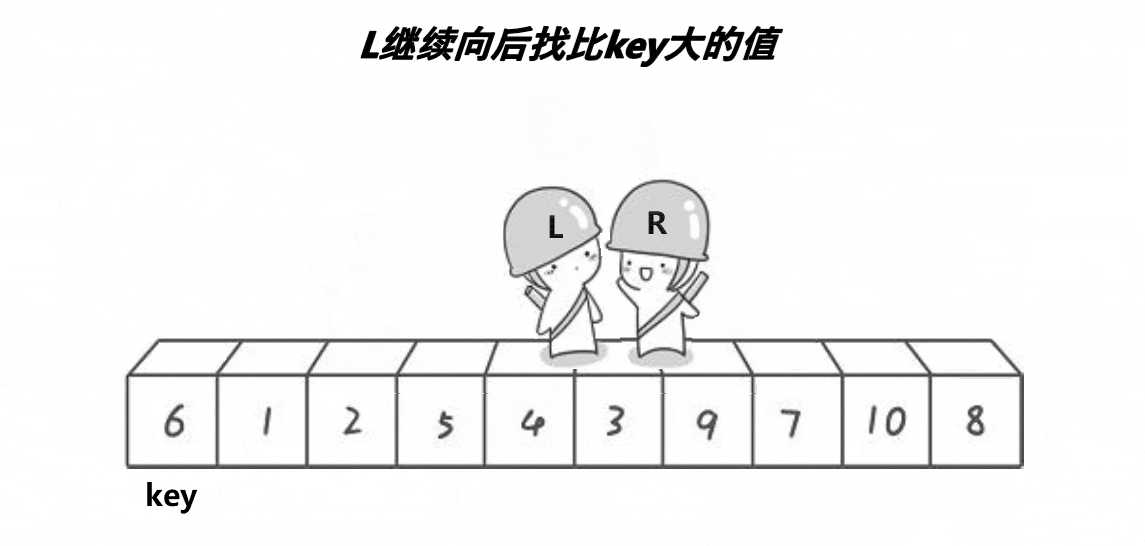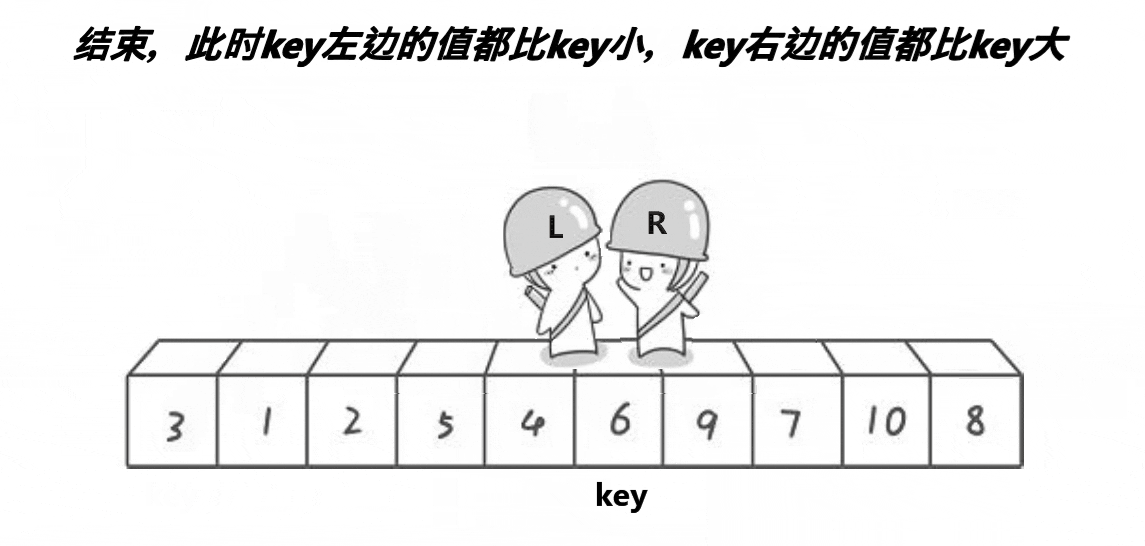
hoare快排思想：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

代码展示：

//三数取中
int GetMidi(int* a,int left, int right)
{int mid = (right - left) / 2;if (a[left] > a[mid]){if (a[right] > a[left]){return left;}else if (a[mid] > a[right]){return mid;}else{return right;}}else // a[left] < a[mid]{if(a[right]>a[mid]){return mid;}else if (a[left] > a[right]){return left;}else{return right;}}
}
//快排
void PartSort1(int* a, int left, int right)
{if (left >= right)return;int begin = left, end = right;//随机数法/*int reti = left + (rand() % (right - left));Swap(&a[left], &a[reti]);*///三数取中法int reti = GetMidi(a,left,right);Swap(&a[left], &a[reti]);int keyi = left;while (left < right){//找小while (left < right && a[right] >= a[keyi])right--;//找大while (left < right && a[left] <= a[keyi])left++;Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);keyi = left;PartSort1(a, begin, keyi - 1);PartSort1(a, keyi + 1, end);
}

根据上面的图可以得出大概的逻辑，left为序列的起始位置下标，right为最后一个数据的下标，选起始位置下标为keyi，right目标是找小于或者等于keyi位置的值，left的目标是找大于或者等于keyi位置的值，right先走，left再走，两个对应的值进行交换，当left等于right时与keyi位置的值交换，就完成了单趟的排序，以keyi位置分为两个区间[left,keyi] keyi [keyi+1,right],接着排这两个区间，排完就排四个区间……，从这里就可以知道使用递归会更好

注意：left和right在走的时候需要满足left小于right。

这里用到三数取中，以及随机取数，这里更推荐三数取中，这两个是对快排的优化，使keyi选择这个序列中更中间的数，更可以提高该算法的效率。

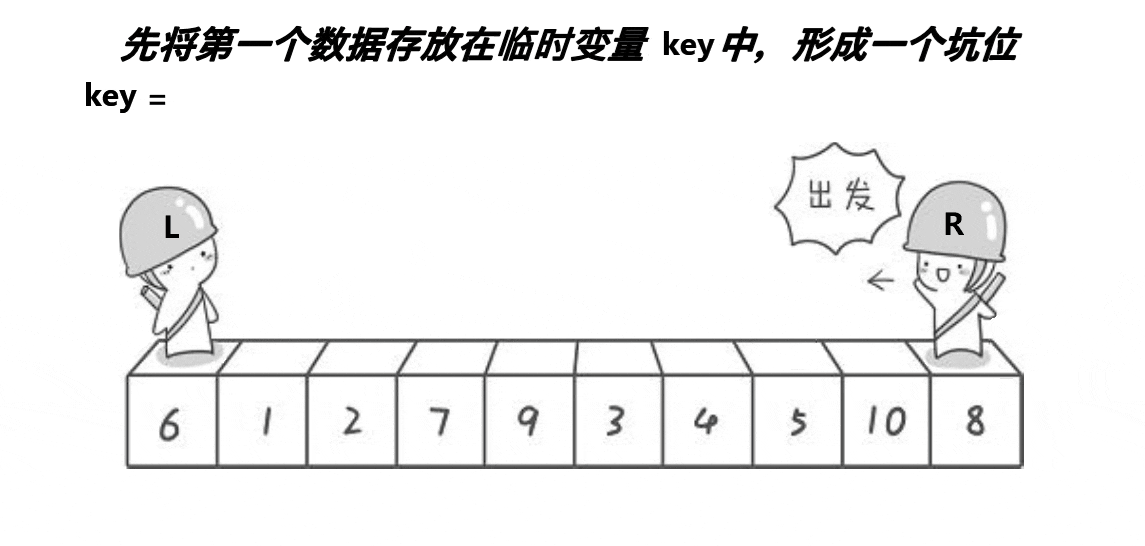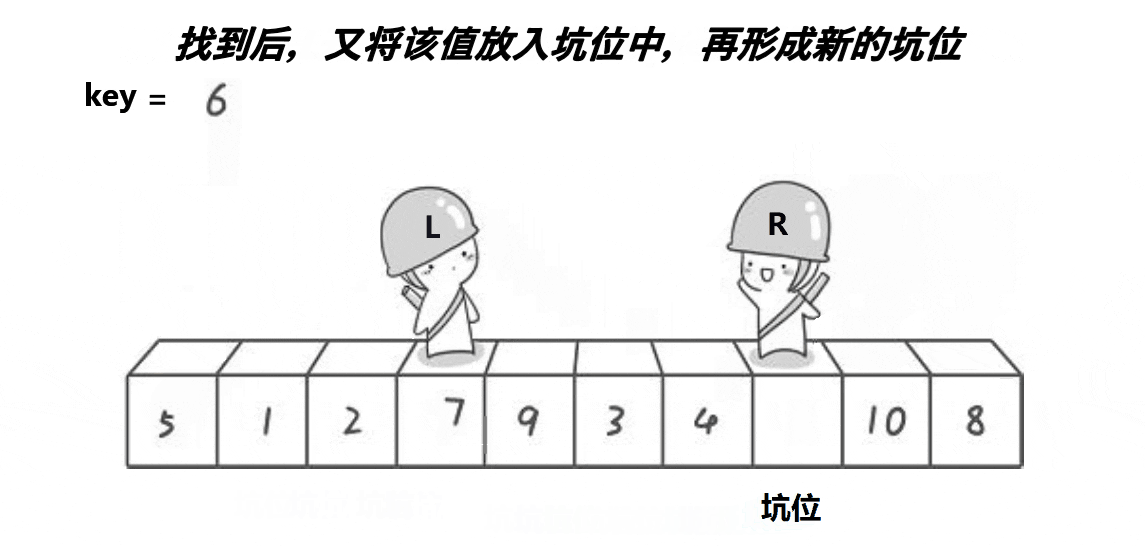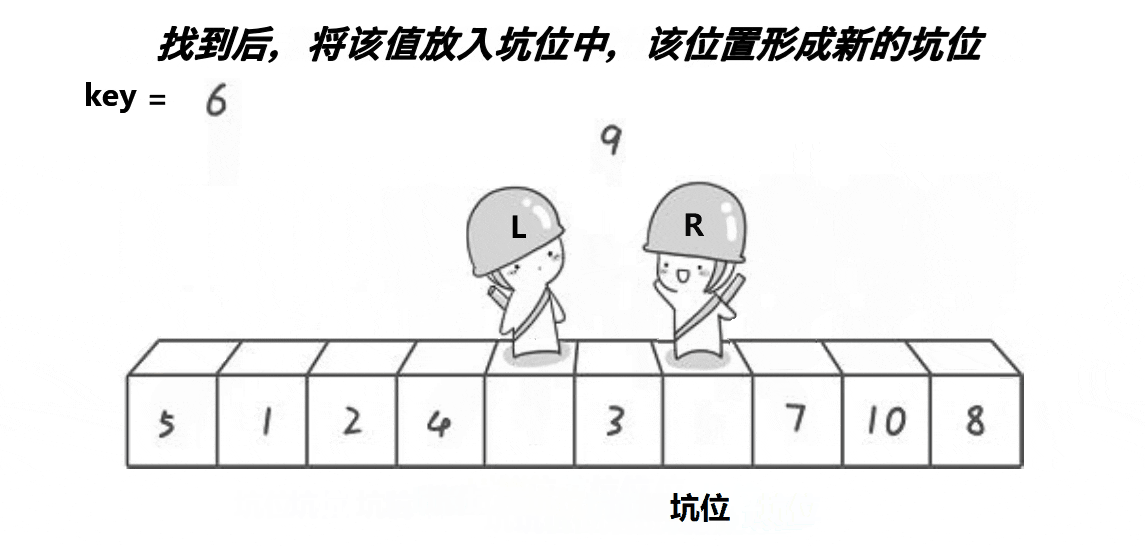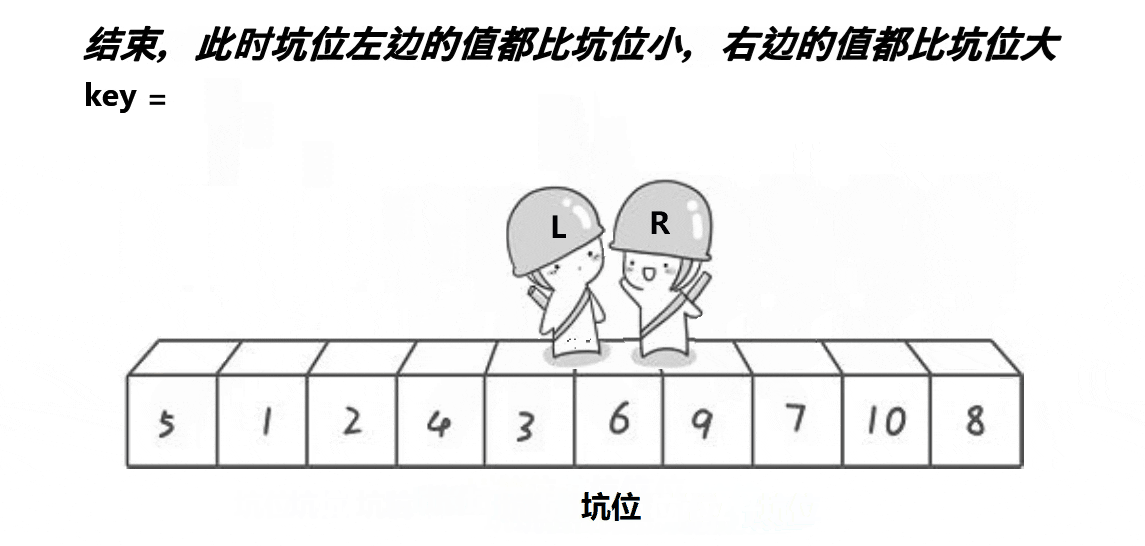
挖坑法

挖坑法key保存的是起始位置（看图中保存的是起始位置的值，因为创建的key是局部变量），当左边为key值，就需要先让右边先走，反之左边先走，定义一个变量key来存放起始位置，right先走，目标是找比key对应值小的值，再把right对应值给left对应值，接着left走，目标是找比key对应值大的值，找到之后把left对应值给right对应值，直到left和right相等，相等位置的值被赋值key对应值，这只是单趟的排序，这里使用递归，与hoare一样分两个、四个……区间，直到left大于或者等于right就返回。

void PartSort2(int* a, int left, int right)
{if (left >= right)return;int begin = left, end = right;//随机数法/*int reti = left + (rand() % (right - left));Swap(&a[left], &a[reti]);*///三数取中法/*int reti = GetMidi(a, left, right);Swap(&a[left], &a[reti]);*/int key = a[left];while (left < right){//找小while (left < right && a[right] >= key)right--;a[left] = a[right];//找大while (left < right && a[left] <= key)left++;a[right] = a[left];}a[left] = key;PartSort1(a, begin, left - 1);PartSort1(a, left + 1, end);
}

当完成一趟排序后，key对应值就到了最终排完后的位置，所以只需要对key对应值前后区间排序就可以，创建两个变量begin和end来存储当前序列的起始位置和末尾，递归时用得上。

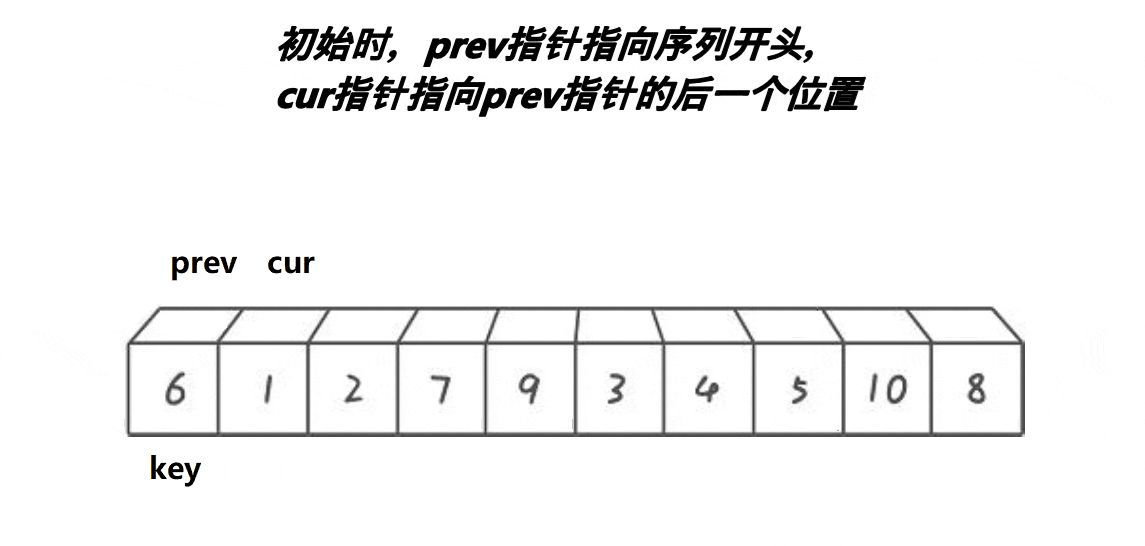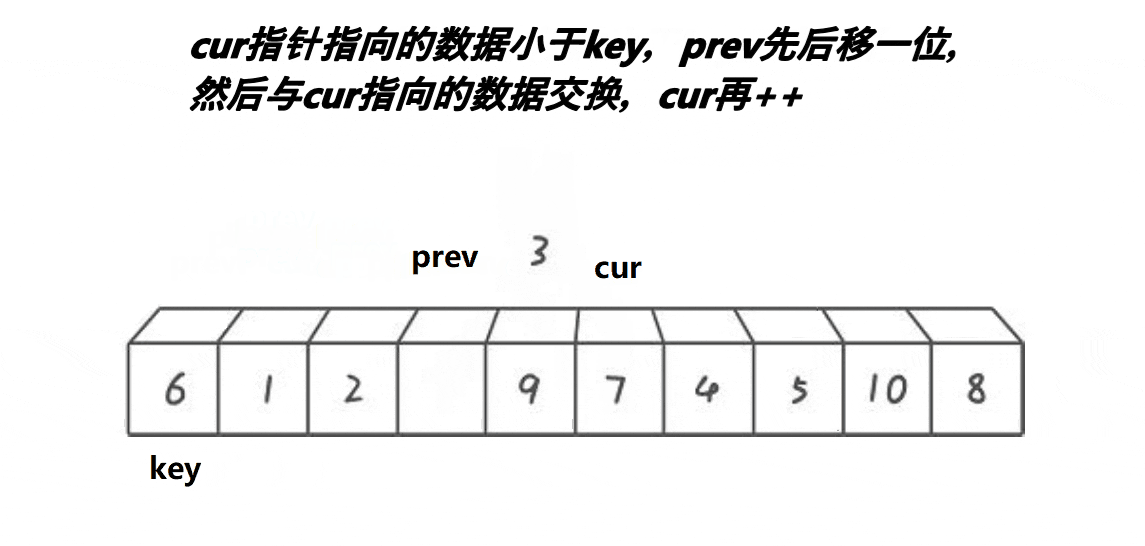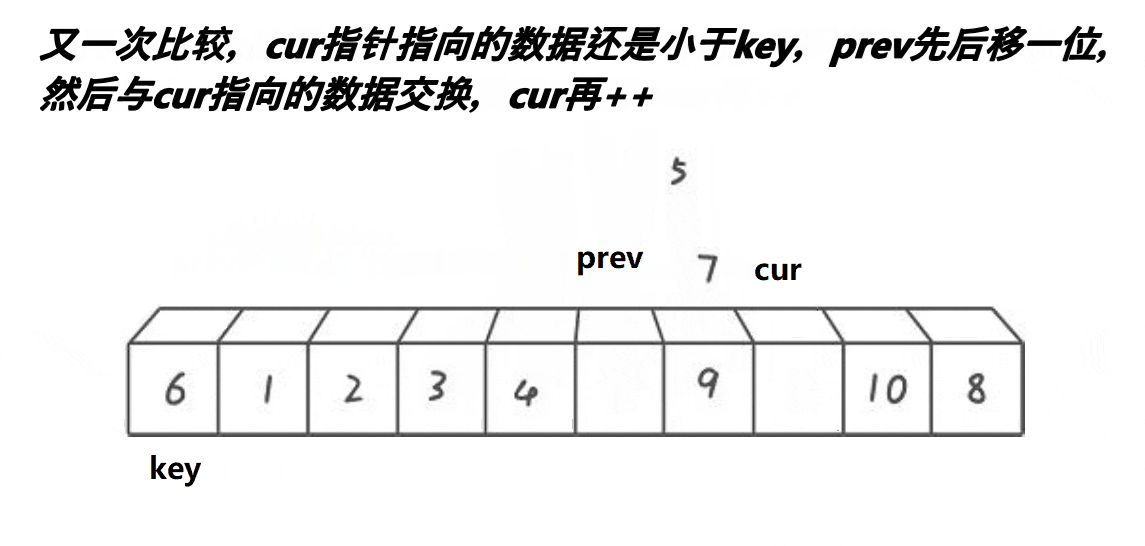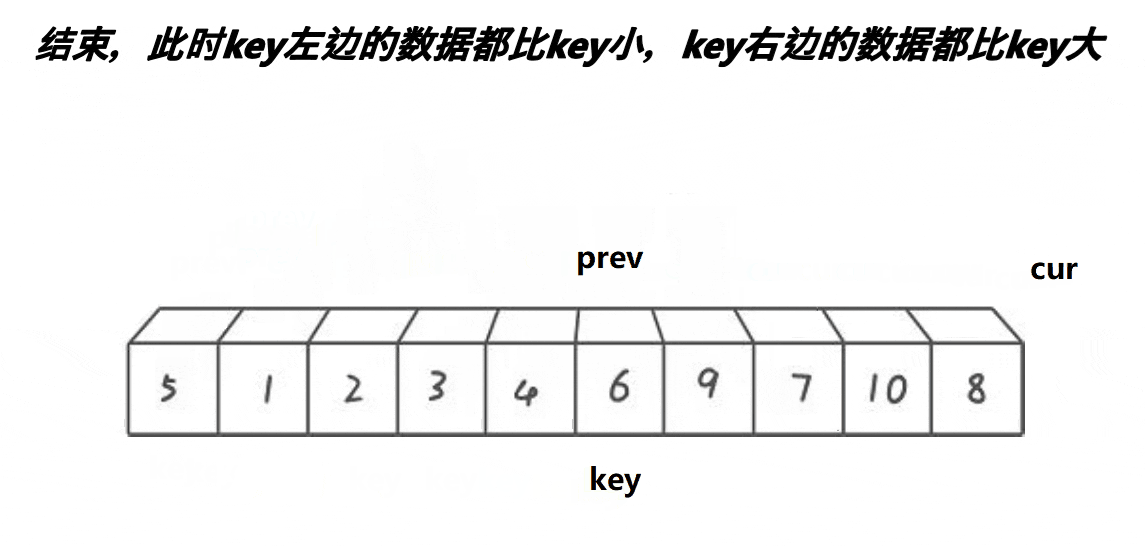
前后指针法

思想：创建两个变量prev和cur，prev在起始位置，cur在prev后一个位置，先对cur对应值和key对应值比较，如果小于key对应值就prev++，然后再交换prev和cur的值，cur++，如果大于key对应值，只cur++。

void PartSort3(int* a, int left, int right)
{if (left >= right)return;int prev = left, cur = left + 1;int keyi = left;while (cur <= right){if (a[cur] < a[keyi]){prev++;Swap(&a[cur],&a[prev]);}cur++;}Swap(&a[keyi], &a[prev]);//优化前/*PartSort3(a, left, prev - 1);PartSort3(a, prev + 1, right);*///优化后if ((right - left + 1) > 10)//在数据量大的时候可以省去很多次递归，分割成很多小区间时使用插入排序。{PartSort3(a, left, prev - 1);PartSort3(a, prev + 1, right);}else{//插入排序InsertSort(a + left, right - left + 1);}
}

创建两个变量prev和cur，prev在起始位置，cur在prev后一个位置，根据上面的思想写出代码，cur需要小于或者等于right，完成单趟就递归，这里进行了优化，因为递归就像二叉树的结构，在最后一层递归数量占一半了，我们可以在递归只剩最后几层时使用直接插入排序就可以增加算法效率，当区间小于十就开始使用插入排序。

时间复杂度：最好情况：O(NlogN)

平均情况：O(NlogN)

最坏情况：O(N^2)

空间复杂度：O(1)

稳定性：不稳定

示例：

归并排序

基本思想：归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

从上面的图可以更好的理解归并排序，将序列逐渐分为一个，再两个两个对比，这时就需要一个新的数组来存放排序后的数据，小的数据先放进新的数组，则每个序列对比时都是有序的，在把两个有序的序列合并成一个新的有序序列，直到将全部的小序列合并成一个有序序列就完成了归并排序。

代码展示：

//归并排序子函数
void _Mergesort(int* a, int left, int right, int* tmp)
{if (left >= right)return;int mid = (right + left) / 2;_Mergesort(a, left, mid, tmp);_Mergesort(a, mid + 1, right, tmp);int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;int j = left;//归并while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}memcpy(a + left, tmp + left, sizeof(int) * (right - left + 1));
}//归并排序函数
void Mergesort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}_Mergesort(a,0,n-1,tmp);free(tmp);
}

归并排序需要分为两个函数，因为这里是写递归的归并，开辟数组只需要开辟一次，所以我们在另一个函数写归并排序，归并排序就相当于后序遍历，先将序列分为一个一个再进行比较。

时间复杂度：O(NlogN)

空间复杂度：O(N)

稳定性：稳定

插入排序

直接插入排序

希尔排序

选择排序

堆排序

冒泡排序

快速排序

hoare版本快排

挖坑法

前后指针法

归并排序

相关文章：