当前位置：首页 > news >正文

解锁动态规划的奥秘：从零到精通的创新思维解析（9）

news 来源：原创 2025/8/21 16:11:31

前言：

小编在前几日写了关于动态规划中的多状态dp的问题，此时小编将会讲述一个动态规划我们常常会遇到的一类问题——股票问题，股票问题就类似小编上一篇所讲述的粉刷房子的问题，可以通过一个二维的dp表来代替多个一维的dp表。买卖股票算是一个很经典的问题了，下面小编简单介绍一下买卖股票问题。

“买卖股票问题”作为动态规划的经典案例，不仅在编程竞赛中频繁出现，也是面试中的常考题目。这类问题以其现实背景的贴近性和解法的多样性著称，不仅考察了对动态规划核心思想的掌握，还能帮助我们深入理解状态转移、子问题划分以及优化策略。

从最基本的一次买卖股票问题，到允许多次买卖甚至设置冷却期和手续费的复杂变体，每一步都体现了动态规划在不同约束条件下的灵活性与精妙性。本篇内容将以逐步深入的方式，剖析买卖股票问题的不同场景，通过数学建模和代码实现，让读者能够全面掌握这一重要的动态规划应用，并在实际问题中灵活运用。

1.买卖股票的最佳时机含冷却期

1.1.题目来源

1.2.题目分析

1.3.思路讲解

1.状态表示

1.2.状态转换方程

3.初始化

4.填表顺序

5.返回值

1.4.代码实操

1.5.代码展示

2.买卖股票的最佳时机含手续费

2.1.题目来源

2.2.题目分析

2.3.思路讲解

1.状态表示

2.状态转换方程

3.初始化

4.填表顺序

5.返回值

2.4.代码书写

2.5.代码展示

3.总结

1.买卖股票的最佳时机含冷却期

1.1.题目来源

本题来自于力扣，下面小编给出相应的链接；309. 买卖股票的最佳时机含冷冻期 - 力扣（LeetCode）

1.2.题目分析

本题的内容比较短，但是包含了许多内容，下面小编简单的概述一下：此时题目给与我们一个数组，此时这个数组里面的内容表示的是第i天时的股票价格，此时我们可以选择不购买当天的股票，或者是购买当天的股票，也可以选择把手头上的股票卖出，只不过本题多了一个限制——我们在卖出股票的第二天是无法购买股票的，因为有1天的冷却期。此时我们需要设计一个算法，这个算法是帮助我们计算我们在买卖股票的最大理论，这便是这个题目让我们去撰写的函数，并且值得一提的是，我们是不可以去参与多笔交易（我们必须在下次购买股票的时候把手头上的股票先卖出去）。

1.3.思路讲解

1.状态表示

此时我们需要一个二维的dp表来表示此时的状态，本题目到是让我们写dp表状态的时候很好入手，无非就是表示买入，可交易，冷冻期三种状态罢了，此时我们可以用dp表的三列来分别表示此时的状态。

dp[i][0]; //第i天结束以后，进入"买入"状态，此时的最大理论。
dp[i][1]; //第i天结束以后，进入"可交易"状态，此时的最大理论。
dp[i][2]; //第i天结束以后，进入"冷冻期"状态，此时的最大理论。

1.2.状态转换方程

此时的状态转换方程其实是本题目的最大难点，因为从题目给定我们的信息我们就可以知道，本题三个状态关系十分的密切，针对于这种情况，此时小编引入了一个小小的模型——状态机。

状态机：动态规划问题中的核心模型

在动态规划的解决方案中，状态机（State Machine）是一个重要的抽象模型，尤其适用于解决问题有明确状态和状态之间的转移规则时。买卖股票问题是应用状态机的典型场景，通过状态机的建模，我们可以清晰地表达状态的变化和转移，从而找到问题的最优解。

状态机是一个由状态（State）和状态转移（State Transition）组成的系统。在动态规划中，状态机通常用来描述问题在不同时间点的可能状态，以及这些状态之间如何通过某种操作发生转移。

在买卖股票问题中，状态机可以用来表示每一天结束时的可能状态，比如“手上有股票”或“手上没有股票”，并用状态转移来表达买入、卖出或保持现状的操作。

下面小编通过图片的方式展示一下状态机的使用方法。

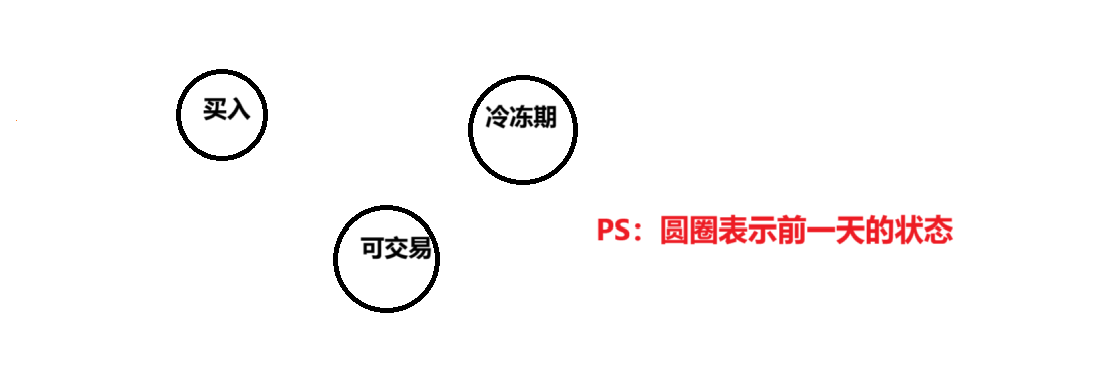
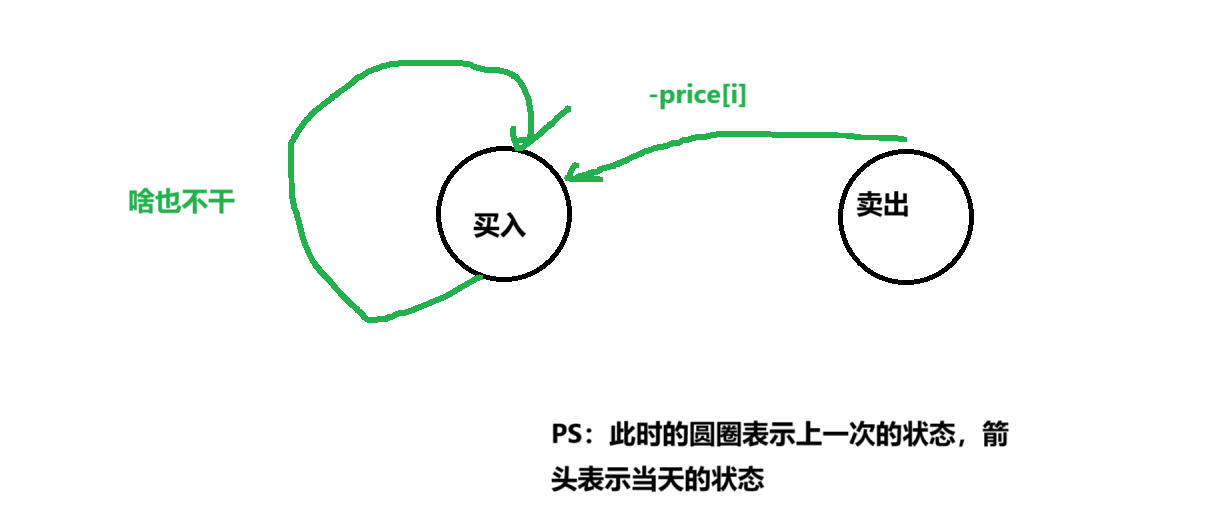
此时我们先来看买入状态，当前一天是买入状态的时候，证明此时已经买入了股票，所以我们可以选择卖出股票进入冷冻期状态；或者是啥也不干，当天还是买入状态。

此时我们在看冷冻期状态，此时如果前一天是冷冻期状态，那么根据题意，第二天仅仅只能是进入可交易状态（手里没股票）。

最后我们再看可交易的状态。如果第二天是可交易状态，那么我们也是有两种选择，分别是：从可交易状态进入买入状态，此时我们需要付费；也可以选择啥也不干，因为股票的价格不好，所以当天还是可交易状态。

所以我们根据状态机便可以很好的去列状态转换方程，如下所示：

dp[i][0] - max(dp[i - 1][0],dp[i - 1][1] - price[i]);//根据箭头指过来的方向
dp[i][1] = max(dp[i - 1][2],dp[i - 1][1]);
dp[i][2] = max(dp[i - 1][0] + price[i]);

3.初始化

初始化是我们在写状态转换方程的时候最主要注意的细节问题，此时我们可以知晓此时当我们选择第一个元素的时候就会出现数组越界的问题，针对于这种问题，小编认为多开辟一行作为虚拟节点是最省事的方式，只不过此时我们需要注意虚拟节点需要填入什么。根据题目，我们可以知道在买入状态的时候，此时手里必须有股票，所以dp[I] [0]应该是-price[i - 1]（注意下标的映射问题哦），其他的两个位置为0即可。

4.填表顺序

从上到下，从左到右。

5.返回值

根据题目，我们仅需返回最后一个位置中最大的元素即可。

1.4.代码实操

此时我们需要设置好一个dp表，此时这个dp表要比原先给定我们的数组要多开辟一行存入虚拟节点。并且给相应的位置进行初始化即可。

int n = prices.size();
vector<vector<int>> dp(n,vector<int>(3,0));
dp[0][0] = -prices[0];

此时我们再根据状态转换方程，通过循环填写数据即可。（一定要注意下标的映射）

for(int i = 1 ; i < n ; i++)
{dp[i][0] = max(dp[i - 1][0],dp[i - 1][1] - prices[i]);dp[i][1] = max(dp[i-1][1],dp[i-1][2]);dp[i][2] = dp[i-1][0] + prices[i];
}

最后，我们返回最后一个位置最大的数据即可。

 return max(dp[n - 1][1],dp[n - 1][2]);

1.5.代码展示

class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> dp(n,vector<int>(3,0));dp[0][0] = -prices[0];for(int i = 1 ; i < n ; i++){dp[i][0] = max(dp[i - 1][0],dp[i - 1][1] - prices[i]);dp[i][1] = max(dp[i-1][1],dp[i-1][2]);dp[i][2] = dp[i-1][0] + prices[i];}return max(dp[n - 1][1],dp[n - 1][2]);}
};

2.买卖股票的最佳时机含手续费

2.1.题目来源

本题还是来自于力扣，下面小编给出具体题目的链接：714. 买卖股票的最佳时机含手续费 - 力扣（LeetCode）

2.2.题目分析

下面就到了喜闻乐见的题目分析环节，本题其实和第一个题高度相似，只不过本题比第一个题要少了冷却期，多了手续费环节，所以此时我们在用状态机分析股票的时候，我们无须在分析三个状态，仅需两个状态我们就可以把这个题目做出来，只不过此时我们在每一次交易完成的时候都需要付手续费，这是和第一个题不同的地方，但是整体来说，本题的难度其实已经算是下降了，下面小编讲述一下本题的理论讲解。

2.3.思路讲解

首先，本题可以通过设置一个二维的dp表或者建立两个一维的dp表来实现本题的思路分析，这里我选用的是两个一维的dp表来实现的，分别叫f表和g表，那么接下来我们就可以按照动态规划五步走来实现本题目的思路讲解。

1.状态表示

此时我们通过题目的定义来对两个表进行正确的状态表示，此时我们可以清晰的知道本题一共就两个状态，分别是买入状态和卖出状态，所以小编此时便对两个表根据之和两个状态进行了定义。

f[i]; //到达i位置的时候，处于买入状态，此时的最大利润。
g[i]; //到达i位置的时候，处于卖出状态，此时的最大理论

2.状态转换方程

此时我们就可以通过状态表示来写出状态转换方程了，不过由于本题的复杂度蛮高的，所以小编还是推荐各位使用状态机来正确表示出状态转换方程，因为状态机可以极大程度上减少我们出错的概率。其状态如下图所示：

如果此时我们当天是买入状态，那么它的前一天可能还是买入状态，或者前一天是卖出状态，通过买股票进入了买入状态。

如果当天是卖出状态，那么前一天可能还是卖出状态，或者前一天是买入状态，只不过此时卖出了股票进入了卖出状态，此时我们有一个值得注意的点，那就是此时我们已经涉及到了手续费问题，因为已经完成了一笔交易，所以我们在得到卖股票的钱的时候，记得把手续费也交一下。

此时我们就完整的写出一个状态机，下面我们就可以根据状态机写出状态转移方程了，此时我们需要取到每一个状态的最大值，因为此时我们要得到最大理论。

f[i] = max(f[i - 1],g[i - 1] - prices[i]);
g[i] = max(g[i - 1],f[i - 1] + prices[i] - fee);

3.初始化

本题的越界问题还是很好发现的，此时当我们是第一个元素的时候，我们无法知道上一个元素的状态，因为上一个元素已经是越界状态了，我们可以根据每一个表的定义，来对第一个位置进行初始化，由于f表代表买入，所以第一个位置的元素肯定是买入了，而g表表示的卖出，因为第一个位置的元素没法卖掉，所以此时我们的g[0]就是0。

f[0] = -pirce[0]; 
g[0] = 0;

4.填表顺序

从左到右依次填写即可。

5.返回值

按理说此时我们返回两个表最后一个位置最大元素即可，但是此时我们通过定义就可以知道此时的f表代表着买入，g表代表着卖出，买入和卖出，仔细一想便可以知道当我们手里没股票的时候，证明此时我们的理论已经是最高了，所以我们仅需返回g表最后一个位置的元素即可。

2.4.代码书写

首先，我们先要创建好两个dp表，它们的大小跟着给定数组的大小一致即可，然后把相应位置的元素进行初始化。

int n = prices.size();
vector<int> f(n); //这个状态表示买入状态，此时手上有股票
vector<int> g(n);  //这个表示卖出状态，此时手上没股票
f[0] = -prices[0];

创建完表后，我们就可以根据之前我们分析的状态转换方程来填表了，此时我们借助循环就可以做到，填完表后，我们返回g表最后一个位置的元素即可。

for(int i = 1 ; i < n ; i++)
{f[i] = max(f[i - 1],g[i - 1] - prices[i]);g[i] = max(g[i - 1],f[i - 1] + prices[i] - fee);
}
return g[n - 1];

2.5.代码展示

class Solution {
public:int maxProfit(vector<int>& prices, int fee) {int n = prices.size();vector<int> f(n); //这个状态表示买入状态，此时手上有股票vector<int> g(n);  //这个表示卖出状态，此时受伤没股票f[0] = -prices[0];for(int i = 1 ; i < n ; i++){f[i] = max(f[i - 1],g[i - 1] - prices[i]);g[i] = max(g[i - 1],f[i - 1] + prices[i] - fee);}return g[n - 1];}
};

3.总结

本文到这里也就结束了，这是小编第一次讲述股票问题，所以内容有问题的话私信我即可，直接在评论区给我指点一下也没有问题，小编在写本文章的时候，已经度过了艰难的期末周，所以我现在十分舒畅，我准备在这几天多产出几篇文章以备不时之需，一起写题的时光总是很短暂的，那么各位大佬们，我们下一篇文章见啦。

1.买卖股票的最佳时机含冷却期

1.1.题目来源

1.2.题目分析

1.3.思路讲解

1.状态表示

1.2.状态转换方程

3.初始化

4.填表顺序

5.返回值

1.4.代码实操

1.5.代码展示

2.买卖股票的最佳时机含手续费

2.1.题目来源

2.2.题目分析

2.3.思路讲解

1.状态表示

2.状态转换方程

3.初始化

4.填表顺序

5.返回值

2.4.代码书写

2.5.代码展示

3.总结

相关文章：