当前位置：首页 > news >正文

决策树简介

news 来源：原创 2025/8/26 19:39:31

【理解】决策树例子

决策树算法是一种监督学习算法，英文是Decision tree。

决策树思想的来源非常朴素，试想每个人的大脑都有类似于if-else这样的逻辑判断，这其中的if表示的是条件，if之后的else就是一种选择或决策。程序设计中的条件分支结构就是if-else结构，最早的决策树就是利用这类结构分割数据的一种分类学习方法。

比如：你母亲要给你介绍男朋友，是这么来对话的：

女儿：多大年纪了？

母亲：26。

女儿：长的帅不帅？

母亲：挺帅的。

女儿：收入高不？

母亲：不算很高，中等情况。

女儿：是公务员不？

母亲：是，在税务局上班呢。

女儿：那好，我去见见。

于是你在脑袋里面就有了下面这张图：

作为女孩的你在决策过程就是典型的分类树决策。相当于通过年龄、长相、收入和是否公务员对将男人分为两个类别：见和不见。

【知道】决策树简介

决策树是什么？

决策树是一种树形结构，树中每个内部节点表示一个特征上的判断，每个分支代表一个判断结果的输出，每个叶子节点代表一种分类结果

决策树的建立过程：

1.特征选择：选取有较强分类能力的特征。

2.决策树生成：根据选择的特征生成决策树。

3.决策树也易过拟合，采用剪枝的方法缓解过拟合。

学习目标：

1.理解信息熵的意义

2.理解信息增益的作用

3.知道ID3树的构建流程

【理解】信息熵

ID3 树是基于信息增益构建的决策树.

定义

熵在信息论中代表随机变量不确定度的度量。
熵越大，数据的不确定性度越高
熵越小，数据的不确定性越低

公式

例子1：假如有三个类别，分别占比为：{1/3,1/3,1/3}，信息熵计算结果为：

例子2：假如有三个类别，分别占比为：{1/10,2/10,7/10}，信息熵计算结果为：

熵越大，表示整个系统不确定性越大，越随机，反之确定性越强。

例子3：假如有三个类别，分别占比为：{1,0,0}，信息熵计算结果为：

$H=-1\log(1)=0$

【理解】信息增益

定义

特征$A$对训练数据集D的信息增益$g(D,A)$，定义为集合$D$的熵$H(D)$与特征A给定条件下D的熵$H(D|A)$之差。即

根据信息增益选择特征方法是：对训练数据集D，计算其每个特征的信息增益，并比较它们的大小，并选择信息增益最大的特征进行划分。表示由于特征$A$而使得对数据D的分类不确定性减少的程度。

例子：

已知6个样本，根据特征a：

特征a	目标值
α	A
α	A
β	B
α	A
β	B
α	B

α 部分对应的目标值为： AAAB

β 部分对应的目标值为：BB

【知道】ID3树构建流程

构建流程：

计算每个特征的信息增益
使用信息增益最大的特征将数据集 S 拆分为子集
使用该特征（信息增益最大的特征）作为决策树的一个节点
使用剩余特征对子集重复上述（1，2，3）过程

案例：

已知：某一个论坛客户流失率数据

需求：考察性别、活跃度特征哪一个特征对流失率的影响更大

分析：

15条样本：5正样本、10个负样本

计算熵
计算性别信息增益
计算活跃度信息增益
比较两个特征的信息增益

1.计算熵

2.计算性别条件熵(a="性别")：

计算性别信息增益(a="性别")

计算活跃度条件熵(a=“活跃度")

计算活跃度信息增益(a=活跃度")

结论：活跃度的信息增益比性别的信息增益大，对用户流失的影响比性别大。

C4.5决策树

学习目标：

1.理解信息增益率的意义

2.知道C4.5树的构建方法

【理解】信息增益率

Gain_Ratio 表示信息增益率
IV 表示分裂信息、内在信息
特征的信息增益 ➗ 内在信息
1. 如果某个特征的特征值种类较多，则其内在信息值就越大。即：特征值种类越多，除以的系数就越大。
2. 如果某个特征的特征值种类较小，则其内在信息值就越小。即：特征值种类越小，除以的系数就越小。

信息增益比本质：是在信息增益的基础之上乘上一个惩罚参数。特征个数较多时，惩罚参数较小；特征个数较少时，惩罚参数较大。惩罚参数：数据集D以特征A作为随机变量的熵的倒数。

【知道】C4.5树构建说明

特征a的信息增益率：

信息增益：1-0.5408520829727552=0.46
特征熵：-4/6*math.log(4/6, 2) -2/6*math.log(2/6, 2)=0.9182958340544896
信息增益率：信息增益/分裂信息=0.46/0.9182958340544896=0.5

特征b的信息增益率：

信息增益：1
特征熵：-1/6*math.log(1/6, 2) * 6=2.584962500721156
信息增益率：信息增益/信息熵=1/2.584962500721156=0.38685280723454163

由计算结果可见，特征1的信息增益率大于特征2的信息增益率，根据信息增益率，我们应该选择特征1作为分裂特征。

CART决策树

学习目标：

1.理解基尼指数的作用

2.知道cart构建的特征选择方法

【知道】Cart树简介

Cart模型是一种决策树模型，它即可以用于分类，也可以用于回归。

分类和回归树模型采用不同的最优化策略。Cart回归树使用平方误差最小化策略，Cart分类生成树采用的基尼指数最小化策略。

【理解】基尼指数计算方法

信息增益（ID3）、信息增益率值越大（C4.5），则说明优先选择该特征。
基尼指数值越小（cart），则说明优先选择该特征。

【理解】基尼指数计算举例

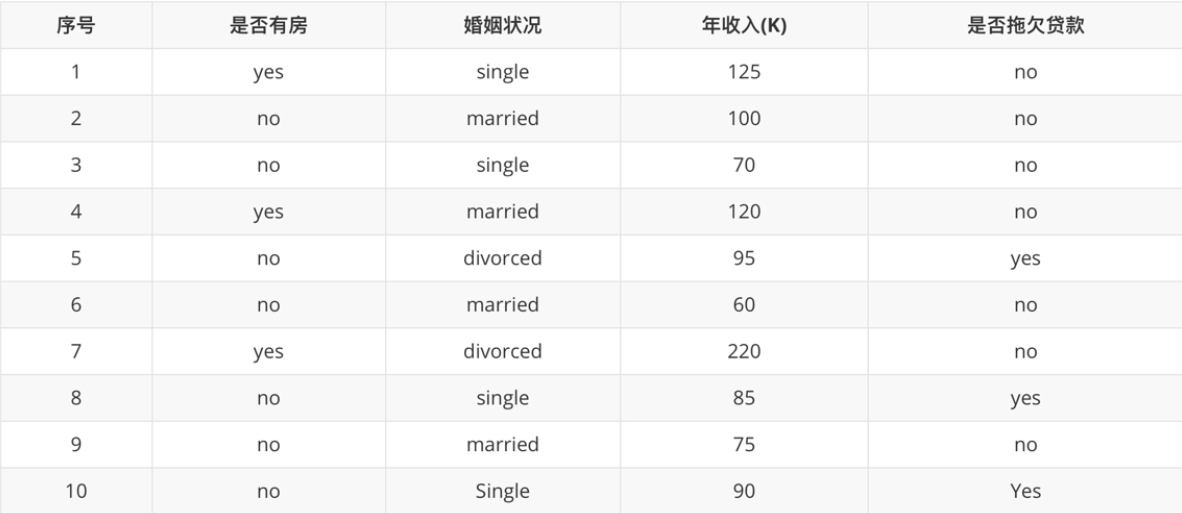
是否有房

计算过程如下：根据是否有房将目标值划分为两部分：

计算有房子的基尼值： 有房子有 1、4、7 共计三个样本，对应：3个no、0个yes
计算无房子的基尼值：无房子有 2、3、5、6、8、9、10 共七个样本，对应：4个no、3个yes
计算基尼指数：第一部分样本数量占了总样本的 3/10、第二部分样本数量占了总样本的 7/10：

婚姻状况

计算 {married} 和 {single,divorced} 情况下的基尼指数：

结婚的基尼值，有 2、4、6、9 共 4 个样本，并且对应目标值全部为 no：

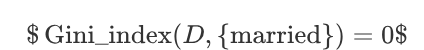
不结婚的基尼值，有 1、3、5、7、8、10 共 6 个样本，并且对应 3 个 no，3 个 yes：

以 married 作为分裂点的基尼指数：
计算 {single} | {married,divorced} 情况下的基尼指数
计算 {divorced} | {single,married} 情况下基尼指数
最终：该特征的基尼值为 0.3，并且预选分裂点为：{married} 和 {single,divorced}

年收入

先将数值型属性升序排列，以相邻中间值作为待确定分裂点：

以年收入 65 将样本分为两部分，计算基尼指数:

重复上面步骤，直到每个叶子结点纯度达到最高.

知道】比较

名称	提出时间	分支方式	特点
ID3	1975	信息增益	1.ID3只能对离散属性的数据集构成决策树 2.倾向于选择取值较多的属性
C4.5	1993	信息增益率	1.缓解了ID3分支过程中总喜欢偏向选择值较多的属性 2.可处理连续数值型属性，也增加了对缺失值的处理方法 3.只适合于能够驻留于内存的数据集,大数据集无能为力
CART	1984	基尼指数	1.可以进行分类和回归，可处理离散属性，也可以处理连续属性 2.采用基尼指数，计算量减小 3.一定是二叉树

回归决策树

学习目标：

1.了解回归决策树的构建原理

2.能利用回归决策树API解决问题

【了解】回归决策树构建原理

CART 回归树和 CART 分类树的不同之处在于:

CART 分类树预测输出的是一个离散值，CART 回归树预测输出的是一个连续值。
CART 分类树使用基尼指数作为划分、构建树的依据，CART 回归树使用平方损失。
分类树使用叶子节点里出现更多次数的类别作为预测类别，回归树则采用叶子节点里均值作为预测输出

CART 回归树构建:

例子：

假设：数据集只有 1 个特征 x, 目标值值为 y，如下图所示：

x	1	2	3	4	5	6	7	8	9	10
y	5.56	5.7	5.91	6.4	6.8	7.05	8.9	8.7	9

由于只有 1 个特征，所以只需要选择该特征的最优划分点，并不需要计算其他特征。

先将特征 x 的值排序，并取相邻元素均值作为待划分点，如下图所示：

| s | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 | 6.5 | 7.5 | 8.5 | 9.5 | | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
计算每一个划分点的平方损失，例如：1.5 的平方损失计算过程为：

R1 为小于 1.5 的样本个数，样本数量为：1，其输出值为：5.56

R2 为大于 1.5 的样本个数，样本数量为：9 ，其输出值为：

该划分点的平方损失：
以此方式计算 2.5、3.5... 等划分点的平方损失，结果如下所示：

s 1.5 2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5
m(s) 15.72 12.07 8.36 5.78 3.91 1.93 8.01 11.73 15.74
当划分点 s=6.5 时，m(s) 最小。因此，第一个划分变量：特征为 X, 切分点为 6.5，即：j=x, s=6.5

s	1.5	2.5	3.5	4.5	5.5	6.5	7.5	8.5	9.5
m(s)	15.72	12.07	8.36	5.78	3.91	1.93	8.01	11.73	15.74

对左子树的 6 个结点计算每个划分点的平方式损失，找出最优划分点：

x	1	2	3	4	5	6
y	5.56	5.7	5.91	6.4	6.8	7.05

s	1.5	2.5	3.5	4.5	5.5
c1	5.56	5.63	5.72	5.89	6.07
c2	6.37	6.54	6.75	6.93	7.05

s	1.5	2.5	3.5	4.5	5.5
m(s)	1.3087	0.754	0.2771	0.4368	1.0644

s=3.5时，m(s) 最小，所以左子树继续以 3.5 进行分裂:

假设在生成3个区域 之后停止划分，以上就是回归树。每一个叶子结点的输出为：挂在该结点上的所有样本均值。

x	1	2	3	4	5	6	7	8	9	10
y	5.56	5.7	5.91	6.4	6.8	7.05	8.9	8.7	9

1号样本真实值 5.56 预测结果：5.72

2号样本真实值是 5.7 预测结果：5.72

3 号样本真实值是 5.91 预测结果 5.72

CART 回归树构建过程如下：

选择第一个特征，将该特征的值进行排序，取相邻点计算均值作为待划分点
根据所有划分点，将数据集分成两部分：R1、R2
R1 和 R2 两部分的平方损失相加作为该切分点平方损失
取最小的平方损失的划分点，作为当前特征的划分点
以此计算其他特征的最优划分点、以及该划分点对应的损失值
在所有的特征的划分点中，选择出最小平方损失的划分点，作为当前树的分裂点

【实践】回归决策树实践

已知数据：

分别训练线性回归、回归决策树模型，并预测对比

训练模型，并使用1000个[0.0, 10]之间的数据，让模型预测，画出预测值图线

从预测效果来看：

1、线性回归是一条直线

2、决策树是曲线

3、树的拟合能力是很强的，易过拟合

决策树剪枝

学习目标：

知道什么是剪枝
理解剪枝的作用
知道常用剪枝方法
了解不同剪枝方法的优缺点

【知道】什么是剪枝?

剪枝 (pruning)是决策树学习算法对付 过拟合 的主要手段。

在决策树学习中，为了尽可能正确分类训练样本，结点划分过程将不断重复，有时会造成决策树分支过多，这时就可能因训练样本学得"太好"了，以致于把训练集自身的一些特点当作所有数据都具有的一般性质而导致过拟合。因此，可通过主动去掉一些分支来降低过拟合的风险。

剪枝是指将一颗子树的子节点全部删掉，利用叶子节点替换子树(实质上是后剪枝技术)，也可以（假定当前对以root为根的子树进行剪枝）只保留根节点本身而删除所有的叶子，以下图为例：

【知道】常见减枝方法汇总

决策树剪枝的基本策略有"预剪枝" (pre-pruning）和"后剪枝"（post- pruning) 。

预剪枝是指在决策树生成过程中，对每个结点在划分前先进行估计，若当前结点的划分不能带来决策树泛化性能提升，则停止划分并将当前结点标记为叶结点;
后剪枝则是先从训练集生成一棵完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶结点。

【理解】例子

在构建树时, 为了能够实现剪枝, 可预留一部分数据用作 "验证集" 以进行性能评估。我们的训练集如下:

验证集如下:

预剪枝

假设: 当前树只有一个结点, 即编号为1的结点. 此时, 所有的样本预测类别为: 其类别标记为训练样例数最多的类别，假设我们将这个叶结点标记为 "好瓜"。此时, 在验证集上所有的样本都会被预测为 "好瓜", 此时的准确率为: 3/7
如果进行此次分裂, 则树的深度为 2, 有三个分支. 在用属性"脐部"划分之后，上图中的结点2、3、4分别包含编号为 {1，2，3， 14}、 {6，7， 15， 17}、 {10， 16} 的训练样例，因此这 3 个结点分别被标记为叶结点"好瓜"、 "好瓜"、 "坏瓜"。此时, 在验证集上 4、5、8、11、12 样本预测正确，准确率为: 5/7。很显然, 通过此次分裂准确率有所提升, 值得分裂.
接下来，对结点2进行划分，基于信息增益准则将挑选出划分属性"色泽"。然而，在使用"色泽"划分后，编号为 {5} 的验证集样本分类结果会由正确转为错误，使得验证集精度下降为 57.1%。于是，预剪枝策略将禁止结点2被划分。
对结点3，最优划分属性为"根蒂"，划分后验证集精度仍为 5/7. 这个划分不能提升验证集精度，于是，预剪枝策略禁止结点3被划分。
对结点4，其所含训练样例己属于同一类，不再进行划分.

于是，基于预剪枝策略从上表数据所生成的决策树如上图所示，其验证集精度为 71.4%. 这是一棵仅有一层划分的决策树。

后剪枝

后剪枝先从训练集生成一棵完整决策树，继续使用上面的案例，从前面计算，我们知前面构造的决策树的验证集精度为42.9%。

首先考察结点6，若将其领衔的分支剪除则相当于把6替换为叶结点。替换后的叶结点包含编号为 {7， 15} 的训练样本，于是该叶结点的类别标记为"好瓜", 此时决策树的验证集精度提高至 57.1%。

然后考察结点5，若将其领衔的子树替换为叶结点，则替换后的叶结点包含编号为 {6，7，15}的训练样例，叶结点类别标记为"好瓜'；此时决策树验证集精度仍为 57.1%. 于是，可以不进行剪枝.
对结点2，若将其领衔的子树替换为叶结点，则替换后的叶结点包含编号为 {1， 2， 3， 14} 的训练样例，叶结点标记为"好瓜"此时决策树的验证集精度提高至 71.4%. 于是，后剪枝策略决定剪枝.
对结点3和1，若将其领衔的子树替换为叶结点，则所得决策树的验证集精度分别为 71.4% 与 42.9%，均未得到提高，于是它们被保留。
最终, 基于后剪枝策略生成的决策树如上图所示, 其验证集精度为 71.4%。

预剪枝优点：

预剪枝使决策树的很多分支没有展开，不单降低了过拟合风险，还显著减少了决策树的训练、测试时间开销

预剪枝缺点：

有些分支的当前划分虽不能提升泛化性能，甚至会导致泛化性能降低，但在其基础上进行的后续划分却有可能导致性能的显著提高
预剪枝决策树也带来了欠拟合的风险

后剪枝优点：

比预剪枝保留了更多的分支。一般情况下，后剪枝决策树的欠拟合风险很小，泛化性能往往优于预剪枝

后剪枝缺点：

但后剪枝过程是在生成完全决策树之后进行的，并且要自底向上地对树中所有非叶子节点进行逐一考察，因此在训练时间开销比未剪枝的决策树和预剪枝的决策树都要大得多。

决策树简介

【理解】决策树例子决策树算法是一种监督学习算法，英文是Decision tree。决策树思想的来源非常朴素，试想每个人的大脑都有类似于if-else这样的逻辑判断，这其中的if表示的是条件，if之后的else就是一种选择或决策。程序设计中的…...

编程日记 2025/8/26 19:39:31

ScrollView（滚动视图）详解和按钮点击事件

文章目录 **ScrollView（滚动视图）详解****1. 核心特性****2. 基本用法****XML 示例：简单滚动布局** **3. 水平滚动：HorizontalScrollView****4. 高级用法****(1) 嵌套滚动控件****(2) 动态添加内容****(3) 监听滚动事件** **5. 注…...

编程日记 2025/8/26 11:10:22

2025年3月，再上中科院1区TOP，“等级熵+状态识别、故障诊断”

引言 2025年3月，研究者在国际机械领域顶级期刊《Mechanical Systems and Signal Processing》（JCR 1区，中科院1区 Top，IF：7.9）上以“Rating entropy and its multivariate version”为题发表科学研究成果。…...

编程日记 2025/8/24 10:29:41

根据pdf文档生成问答并进行评估

目标是根据pdf文档生成问答，并进行评估。首先，安装依赖 pip install PyPDF2 pandas tqdm openai -q 具体过程如下： 1、将pdf放在opeai_blog_pdfs目录下，引用依赖 2、上传pdf文件，创建向量库 3、单个提问的向量检索…...

编程日记 2025/8/26 19:32:27

计算机网络 - 四次挥手相关问题

通过一些问题来讨论 TCP 的四次挥手断开连接说一下四次挥手的过程？为什么需要四次呢？time-wait干嘛的，close-wait干嘛的，在哪一个阶段？状态CLOSE_WAIT在什么时候转换成下一个状态呢？为什么 TIME-WAIT 状态…...

编程日记 2025/8/26 19:30:10

SLAM | 两组时间戳不同但同时开始的imu如何对齐

场景： 两个手机在支架上，同时开始采集数据需求： 对齐两个数据集的imu数据做到A图片 B imu 做法： 取出来两组imu数据到excel表中，画图 A组 B组： x轴 ： 所有imu的时间戳减去第一个时间…...

编程日记 2025/8/26 19:30:12

code review时线程池的使用

一、多线程的作用多个任务并行执行可以提升效率异步，让与主业务无关的逻辑异步执行，不阻塞主业务二、问题描述 insertSelective()方法是一个并发度比较高的业务，主要是插入task到任务表里，新建task，并且insertSele…...

编程日记 2025/8/23 4:28:38

物流网络暗战升级DHL新布局将如何影响eBay卖家库存分布策略？

物流网络暗战升级：DHL新布局将如何影响eBay卖家库存分布策略？ 跨境电商发展迅猛，卖家对物流的依赖程度不言而喻。尤其是平台型卖家，例如在eBay上经营多站点的卖家，物流成本和时效几乎直接决定了利润空间与客户满意度。…...

编程日记 2025/8/23 11:57:23

JAMA Netw. Open：机器学习解码大脑：精准预测PTSD症状新突破

创伤后应激障碍（PTSD）是一种常见的心理健康状况，它可以在人们经历或目睹创伤性事件（如战争、严重事故、自然灾害、暴力攻击等）后发展。PTSD的症状可能包括 flashbacks（闪回）、噩梦、严重的焦虑、…...

编程日记 2025/8/20 22:42:21

域控制器升级的先决条件验证失败,证书服务器已安装

出现“证书服务器已安装”导致域控制器升级失败时，核心解决方法是卸载已安装的证书服务‌。具体操作如下：‌ ‌卸载证书服务‌ 以管理员身份打开PowerShell，执行命令： Remove-WindowsFeature -Name AD-Certificate该命令会移除A…...

编程日记 2025/8/24 16:03:49

Node.js入门

Node.js入门 html,css,js 30年了 nodejs环境 09年出现 15年 nodejs为我们解决了2个方面的问题： 【锦上添花】让我们前端工程师拥有了后端开发能力（开接口，访问数据库） - 大公司BFF（50）【✔️】前端工程…...

编程日记 2025/8/22 19:21:30

使用CubeMX新建EXTI外部中断工程——不使用回调函数

具体的使用CubeMX新建工程的步骤看这里：STM32CubeMX学习笔记（3）——EXTI(外部中断)接口使用_cubemx exti-CSDN博客之前一直都是在看野火的视频没有亲手使用CubeMX生成工程，而且野火给的例程代码框架和自动生成的框架也不一样&…...

编程日记 2025/8/21 23:14:06

1、可变系数除法实现----利用除法的本质 timescale 1ns / 1ps // // Company: // Engineer: // // Create Date: 2025/04/15 13:45:39 // Design Name: // Module Name: divide_1 // Project Name: // Target Devices: // Tool Versions: // Description: // // Depe…...

编程日记 2025/8/17 19:05:04

win32汇编环境,网络编程入门之十九

;win32汇编环境,网络编程入门之十九 ;在这一编程里，我们学习一下如何使用gethostbyname函数，也顺便学一下如何将C定义的函数在WIN32汇编环境中使用 ;先看一下官方解释：从主机数据库中检索与主机名对应的主机信息。 ;它的原理是从你的电脑DNS中…...

编程日记 2025/8/26 19:37:11

Java学习手册：Java线程安全与同步机制

在Java并发编程中，线程安全和同步机制是确保程序正确性和数据一致性的关键。当多个线程同时访问共享资源时，如果不加以控制，可能会导致数据不一致、竞态条件等问题。本文将深入探讨Java中的线程安全问题以及解决这些问题的同步机制。线程安…...

编程日记 2025/8/25 6:45:51

在生信分析中，从生物学数据库中下载的序列存放在哪里？要不要建立一个小型数据库，或者存放在Gitee上？

李升伟整理在Galaxy平台中使用时，从NCBI等生物学数据库下载的DNA序列的存储位置和管理方式需要根据具体的工作流程和需求进行调整。以下是详细的分步说明和建议： 一、Galaxy中DNA序列的默认存储位置在Galaxy的“历史记录”（History&…...

编程日记 2025/8/20 2:26:08

Python异步编程入门：Async/Await实战详解

引言在当今高并发的应用场景下，传统的同步编程模式逐渐暴露出性能瓶颈。Python通过asyncio模块和async/await语法为开发者提供了原生的异步编程支持。本文将手把手带你理解异步编程的核心概念，并通过实际代码案例演示如何用异步爬虫提升10倍效率&#…...

编程日记 2025/8/26 19:37:10

cmd 终端输出乱码问题 |Visual Studio 控制台输出中文乱码解决

在网上下载，或者移植别人的代码到自己的电脑，使用VS运行后，控制台输出中文可能出现乱码。这是因为源代码的编码格式和控制台的编码格式不一致。文章目录查看源代码文件编码格式查看输出控制台编码格式修改编码格式修改终端代码页补充总结 …...

编程日记 2025/8/24 5:58:17

【算法】椭圆曲线签名（ECDSA）

🤔什么是椭圆曲线签名（ECDSA）？ 椭圆曲线签名算法（Elliptic Curve Digital Signature Algorithm，简称 ECDSA）是一种基于椭圆曲线密码学的数字签名算法。它主要用于加密货币（如 Bit…...

编程日记 2025/8/26 19:37:10

Linux下使用MTK的SP_Flash_tool刷机工具

MTK的SP_Flash_tool刷机工具安装流程如下： 1、解压SP_Flash_Tool_Linux_v5.1336.00.100_Customer.zip unzip SP_Flash_Tool_exe_Linux_64Bit_v5.1520.00.100.zip 2、首先安装 libusb-dev 这个包： sudo apt-get install libusb-dev 3、安装成功之后…...

编程日记 2025/8/26 19:34:49

FRP内网穿透代理两个web页面（多端口内网穿透）

内网机器代理两个web页面出来下载frp 选择0.51.2版本下载，高版本测试为成功 frp下载地址部署frp server端（公网部署） #上传到opt rootsdgs-server07:/opt# ll frp_0.51.2_linux_amd64.tar.gz -rw-r--r-- 1 root root 11981480 Apr 15 1…...

编程日记 2025/8/25 0:21:16

Jenkins插件下载慢解决办法

jenkins设置插件使用国内镜像_jenkins 国内镜像-CSDN博客国内源以下是一些常用的国内 Jenkins 插件更新源地址： 清华大学：https://mirrors.tuna.tsinghua.edu.cn/jenkins/updates/update-center.json华为开源镜像站：https://mirrors.huawei…...

编程日记 2025/8/26 19:39:30

【Unity笔记】Unity开发笔记：ScriptableObject实现高效游戏配置管理（含源码解析）

在Unity开发中，高效管理游戏配置数据是提升开发效率的关键。本文分享如何使用ScriptableObject构建可编辑的键值对存储系统，并实现运行时动态读取。一、为什么选择ScriptableObject？ 1.1 ScriptableObject的核心优势独立资源：…...

编程日记 2025/8/22 4:39:09

FPAG IP核调用小练习

一、调用步骤 1、打开Quartus 右上角搜索ROM，如图所示 2、点击后会弹出如图所示其中文件路径需要选择你自己的 3、点击OK弹出如图所示图中红色改为12与1024 4、然后一直点NEXT，直到下图这里要选择后缀为 .mif的文件 5、用C语言生成 .mif文件 //…...

编程日记 2025/8/26 19:30:11

vue动画

1、动画实现 （1）、操作css的transition或animation （2）、在插入、更新或移除DOM元素时，在合适的时候给元素添加样式类名 （3）、过渡的相关类名： xxx-enter-active: 进入的时候激活…...

编程日记 2025/8/21 12:13:20

大数据学习（106）-hivesql函数

🍋🍋大数据学习🍋🍋 🔥系列专栏： 👑哲学语录: 用力所能及，改变世界。 💖如果觉得博主的文章还不错的话，请点赞👍收藏⭐️留言📝支持一…...

编程日记 2025/8/26 19:37:12

AI日报 - 2025年04月16日

🌟 今日概览(60秒速览) ▎🤖 模型井喷 | OpenAI (o3/o4-mini, GPT-4.1), Meta (Llama 4 Scout/Maverick), Z.ai (GLM-4家族), Cohere (Embed 4), Google (DolphinGemma) 等发布新模型，多模态、长文本、高效推理成焦点。 ▎💼 商业…...

编程日记 2025/8/19 2:48:49

C# 经纬度坐标的精度及WGS84(谷歌)、GCJ02(高德)、BD09(百度)坐标相互转换（含高精度转换）

1. 概述 WGS-84坐标系（World Geodetic System一1984 Coordinate System）是一种国际上采用的地心坐标系，GCJ-02是由中国国家测绘局（G表示Guojia国家，C表示Cehui测绘，J表示Ju局）制订的地理信息系…...

编程日记 2025/8/20 18:36:11

案例：陌陌聊天数据分析

背景分析： 陌陌作为聊天平台每天都会有大量的用户在线，会出现大量的聊天数据，通过对聊天数据的统计分析 ，可以更好的对用户构建精准的用户画像 ，为用户提供更好的服务以及实现高 ROI 的平台运营推广&#xff…...

编程日记 2025/8/22 4:47:31

关闭谷歌浏览器（Google Chrome）的自动更新可以通过以下方法实现。具体操作步骤取决于你的操作系统。

关闭谷歌浏览器（Google Chrome）的自动更新可以通过以下方法实现。具体操作步骤取决于你的操作系统。 1. 在 Windows 上关闭 Chrome 自动更新2. 在 macOS 上关闭 Chrome 自动更新3. 在 Linux 上关闭 Chrome 自动更新4. 注意事项1. 在 Windows 上关闭 Chro…...

编程日记 2025/8/23 5:05:10

进程（完）

今天我们就补充一个小的知识点,查看进程树命令,来结束我们对linux进程的学习,那么话不多说,来看. 查看进程树 pstree 基本语法： pstree [选项] 优点：可以更加直观的来查看进程信息常用选项： -p：显示进程的pid -u&#xff…...

编程日记 2025/8/26 19:34:47

（劳特巴赫调试器学习笔记）四、Practice脚本.cmm文件编写

Lauterbach调试器文章目录 Lauterbach调试器一、什么是Practice脚本文件二、cmm脚本使用示例总结一、什么是Practice脚本文件官方文档解释： 因为Practice脚本以cmm为后缀，所以大多数人叫它cmm脚本。以tricore为例，在安装目录下&#xff…...

编程日记 2025/8/22 9:52:24

并行流parallelStream.map().collect()

一、使用场景先贴代码 public static void main(String[] args) {List<String> stringList new ArrayList<>();List<Integer> integerList new ArrayList<>();int num 10000;for (int i 0;i<num;i){stringList.add(String.valueOf(i));}stri…...

编程日记 2025/8/25 3:29:14

2025最新版flink2.0.0安装教程（保姆级）

Flink支持多种安装模式。 local（本地）——本地模式 standalone——独立模式，Flink自带集群，开发测试环境使用 standaloneHA—独立集群高可用模式，Flink自带集群，开发测试环境使用 yarn——计算资源统一…...

编程日记 2025/8/26 12:50:33

软件测试小讲

大家好，我是程序员小羊！ 前言： 在 Web 项目开发中，全面的测试是保证系统稳定性、功能完整性和良好用户体验的关键。下面是一个详细的 Web 项目测试点列表，涵盖了不同方面的测试： 1. 功能测试确保应用…...

编程日记 2025/8/26 19:39:29

DP35 【模板】二维前缀和 ---- 前缀和

目录一：题目二：算法原理三：代码实现一：题目题目链接：【模板】二维前缀和_牛客题霸_牛客网二：算法原理三：代码实现 #include <iostream> #include <vector> using name…...

编程日记 2025/8/21 13:42:31

C语言——分支语句

在现实生活中，我们经常会遇到作出选择和判断的时候，在C语言中也同样要面临作出选择和判断的时候，所以今天，就让我们一起来了解一下，C语言是如何作出选择判断的。目录 1.何为语句？ 2.if语句 2.1 if语句的…...

编程日记 2025/8/24 16:36:19

使用Docker安装Jenkins

1、准备 2、安装详见： https://www.jenkins.io/doc/book/installing/ https://www.jenkins.io/zh/doc/book/installing/ https://www.jenkins-zh.cn/tutorial/get-started/install/ # 方式1： # 详见：https://www.jenkins.io/doc/book/inst…...

编程日记 2025/8/25 15:49:47

东方博宜OJ ——2395 - 部分背包问题

贪心入门 ————2395 - 部分背包问题 2395 - 部分背包问题题目描述输入输出样例问题分析贪心算法思路代码实现总结 2395 - 部分背包问题题目描述阿里巴巴走进了装满宝藏的藏宝洞。藏宝洞里面有 N (N < 100)堆金币，第i堆金币的总重量和总价值分别是mi,vi (l …...

编程日记 2025/8/20 7:40:49

【期中准备特辑】计组，电路，信号

计组以点带面地复习书中内容！ 指令体系结构（ISA）是计算机硬件和软件的分界面世界上第一台电子计算机是 ENIAC（埃尼阿克） 第一代计算机采用电子管作为主要器件；第二代计算机采用晶体管；第三代…...

编程日记 2025/8/25 20:45:23

经典算法判断一个图是不是树

判断一个图是不是树问题描述给一个以0 0结尾的整数对列表，除0 0外的每两个整数表示一条连接了这两个节点的边。假设节点编号不超过100000大于0。你只要判断由这些节点和边构成的图是不是树。是输出YES，不是输出NO。输入样例1 6 8 5 3 5 2 6 4 5…...

编程日记 2025/8/26 13:22:37

力扣 283 移动零的两种高效解法详解

目录方法一：两次遍历法方法二：单次遍历交换法两种方法对比在解决数组中的零移动到末尾的问题时，我们需要保持非零元素的顺序，并原地修改数组。以下是两种高效的解法及其详细分析。方法一：两次遍历法思路分析…...

编程日记 2025/8/20 23:14:48

代码随想录第18天：二叉树

一、修剪二叉树（Leetcode 669） 递归法 class Solution:def trimBST(self, root: TreeNode, low: int, high: int) -> TreeNode:# 如果当前节点为空，直接返回空节点（递归终止条件）if root is None:return None# 如果…...

编程日记 2025/8/20 7:23:18

KMP算法核心笔记：前后缀本质与nextval实现

KMP算法核心笔记：前后缀本质与nextval实现核心疑问：为什么用「前后缀」而非「最大子串」？ 1. 结构唯一性前后缀限定在字符串首尾区域，最大子串可位于任意位置只有前后缀能保证滑动后的有效对齐 2. 移动确定性文本&#xf…...

编程日记 2025/8/22 16:03:00

Breeze 40A FOC 电调：Vfast 观测器技术赋能无人机精准动力控制

核心技术特性 1. 全新Vfast 观测器技术基于先进矢量控制算法（FOC 驱动），实现电机状态实时精准观测，适配性优于传统 FOC 方案，兼容主流无人机动力配置。高效算法设计，输出功率与力效超越多数方波电调&…...

编程日记 2025/8/22 2:22:57

如何处理ONLYOFFICE文档服务器与Java Web应用间的安全认证和授权

如何处理ONLYOFFICE文档服务器与Java Web应用间的安全认证和授权？ 处理 ONLYOFFICE 文档服务器与 Java Web 应用之间的安全认证和授权，通常涉及以下几个关键步骤和技术： 1. JWT (JSON Web Token) 认证启用 JWT： ONLYOFFICE 文档…...

编程日记 2025/8/21 21:09:36

手机上的PDF精简版：随时随地享受阅读

在移动互联网时代，随时随地阅读电子书和文档已经成为许多人的习惯。无论是学习、工作还是娱乐，一款好用的PDF阅读器都是必不可少的工具。今天，我们要介绍的思读PDF精简版，就是这样一款简洁而强大的PDF阅读工具，能够让…...

编程日记 2025/8/21 7:28:50

XCTF-web（一）

view_source F12ctrluctrlshiftiURL前添加：view-source:curl http://192.168.1.1robots 根据题目提示，查看一下robots.txt /flag_ls_h3re.php backup /index.php.bak ┌──(kali㉿kali)-[~] └─$ cat index.php.bak <html> <…...

编程日记 2025/8/23 1:50:09

字节跳动开源 Godel-Rescheduler：适用于云原生系统的全局最优重调度框架

背景在云原生调度中，一次调度往往无法解决所有问题，需要配合重调度来优化资源分配和任务摆放。传统的重调度框架主要集中在识别异常节点或任务，并通过迁移或删除来解决。然而，这些框架往往只能解决局部问题，无法提供…...

编程日记 2025/8/25 14:17:48

贪心算法day9（合并区间）

1.合并区间 56. 合并区间 - 力扣（LeetCode） 对于这种区间问题，我们应该先排序根据排序的结果总结一些规律，进而的得出解决该问题的策略。 class Solution {public static int[][] merge(int[][] intervals) {//第一步进行左端点…...

编程日记 2025/8/19 11:34:35

【理解】决策树例子

【知道】决策树简介

【理解】信息熵

【理解】信息增益

【知道】ID3树构建流程

C4.5决策树

【理解】信息增益率

【知道】C4.5树构建说明

CART决策树

【知道】Cart树简介

【理解】基尼指数计算方法

【理解】基尼指数计算举例

是否有房

婚姻状况

年收入

知道】比较

回归决策树

【了解】回归决策树构建原理

【实践】回归决策树实践

决策树剪枝

【知道】什么是剪枝?

【知道】常见减枝方法汇总

【理解】例子

预剪枝

后剪枝

相关文章：