当前位置：首页 > news >正文

C++红黑树

news 来源：原创 2025/8/28 12:03:20

一、红黑树的概念

二、红黑树的定义

三、红黑树的实现

一、红黑树的概念

红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或者Black。通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出两倍，因而是接近平衡的。

1.1红黑树的性质

1.每个结点不是红色就是黑色

2.根节点是黑色的

3.如果一个节点是红色的，则它的两个孩子结点是黑色的(不能出现连续的红色节点，父子节点：黑+黑/黑+红)

4.对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点(每条路径都包含相同数量的黑色节点)

5.每个叶子结点都是黑色的(此处的叶子结点指的是空结点)->方便数路径

注：路径是从根节点走到空

像这样的红黑树看似只有四条路径，实际上有八条路径，原因就是算上了空结点如下图

这也是为了更好地判断红黑树，避免混淆

像这个就不是红黑树，原因就是分出来红色那条线也算一条路径

那为什么能保证最长路径是最短路径的二倍呢？

最短路径:全黑

最长路径：一黑一红

假设每条路径都有N个黑色节点

每条路径的节点数量在N-2N之间

二、红黑树的定义

enum Color
{Red,Black
};
template<class K, class V>
struct RBTreenode
{RBTreenode<K, V>* _left;RBTreenode<K, V>* _right;RBTreenode<K, V>* _parent;pair<K, V> _kv;Color _col;RBTreenode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(Red){}
};

2.1插入

大致的插入代码上和AVL数差不多，具体的大家可以看一下我的AVL搜索树的这篇文章

https://mpbeta.csdn.net/mp_blog/creation/editor/147169928https://mpbeta.csdn.net/mp_blog/creation/editor/147169928那我们再想一下新增节点是红色的还是黑色的

如果我们在一条路径上新增的是黑色节点，那么势必会影响到所有的路径，因为每条路径的黑色节点是固定的，如果你新增的是红色节点，只会影响父亲，我们只需要根据规则灵活改变就行了

那我们选择了新增节点是红色的以后，分以下两种情况来讨论

1.新增节点父亲是黑色的，那么插入结束，不需要处理

2.新增节点父亲是红色的，需要处理（变色）/(旋转+变色)

我们看新增一个红色节点，如果父亲是红色的，那违反规则我们就把它变黑色，但是这条路径多了一个黑色节点，我们要减少一个黑色节点，把6变红，但是6的左边少了一个黑色节点，所有我们把5变黑，这只是最简单的一种情况

5是新增节点，如果我们还按上面的方法来把6变黑，把4变红，但是4的左没有节点了，就无法达到黑色节点平衡，这时候我们就要用到AVL树里面的双旋，旋转+变色

我们这里先双旋完，看就符合我们上面的步骤了

结论：关键看的是叔叔

cur为当前节点，f为父节点，g为祖父节点，u为叔叔节点

情况一：cur为红，f为红，g为黑，u存在且为红

解决方式:将f,u改为黑，g改为红，然后把g当成cur，继续向上调整

如果g是根，那把g变为黑色没问题；

如果g不是根，如果不把g变黑就会凭空多出一个黑色节点，所以我们变红，但是插入之前g是黑，我们继续要向上看，如果g的上面是黑那不用调整，如果是红还要继续向上调整

我们再把这个图拿出来细分一下

a，b是一个红节点，新增插入一个红节点，插入在a，b孩子热议位置，都引发变色+向上处理

像在这里的话，如果我们在b位置插入，插入节点就是cur，b就是f，a就是u，g就是之前的cur

所以说cur不一定是新增，也有可能是a，b的爷爷

那有多少种情况呢

cde形状组合:4*4*4

插入位置：4个位置

合计组合：256种情况，如果每条路径有两个黑色节点，那将是指数级增长，所以情况是很多的，才引申出来的抽象图

情况二：cur为红，f为红，g为黑，u不存在/u存在且为黑

如果u存在且为黑

如果我们要继续更改父亲变成黑色的话，黑色节点就无法控制了，就是你把f变黑，凭空多出一个黑色节点，用g变红来抵消，但是u的路径上就少了一个黑色节点，但是u本身也是黑色节点无法改变，这时候我们也仔细看一下最长路径已经超过最短路径的2倍了，所以我们要旋转+变色

解决方案：

f为g的左孩子，cur为f的左孩子，则针对f进行右单旋；

f为g的右孩子，cur为f的右孩子，则针对f进行左单旋

f、g变色--f变黑，g变红

那上面这种我们能不能换一种方案

不好，因为它不是终结态，f是红我们还要继续向上更新判断，f是黑我们就不用继续在向上更新了

情况三：cur为红，f为红，g为黑，u不存在且为黑

这种情况其实和上面是类似的，无非就是旋转的问题而已

解决方案：

f为g的左孩子，cur为f的右孩子，则针对f进行左单旋；

f为g的右孩子，cur为f的左孩子，则针对f进行右单旋

就转换为了情况2

最终呈现的是

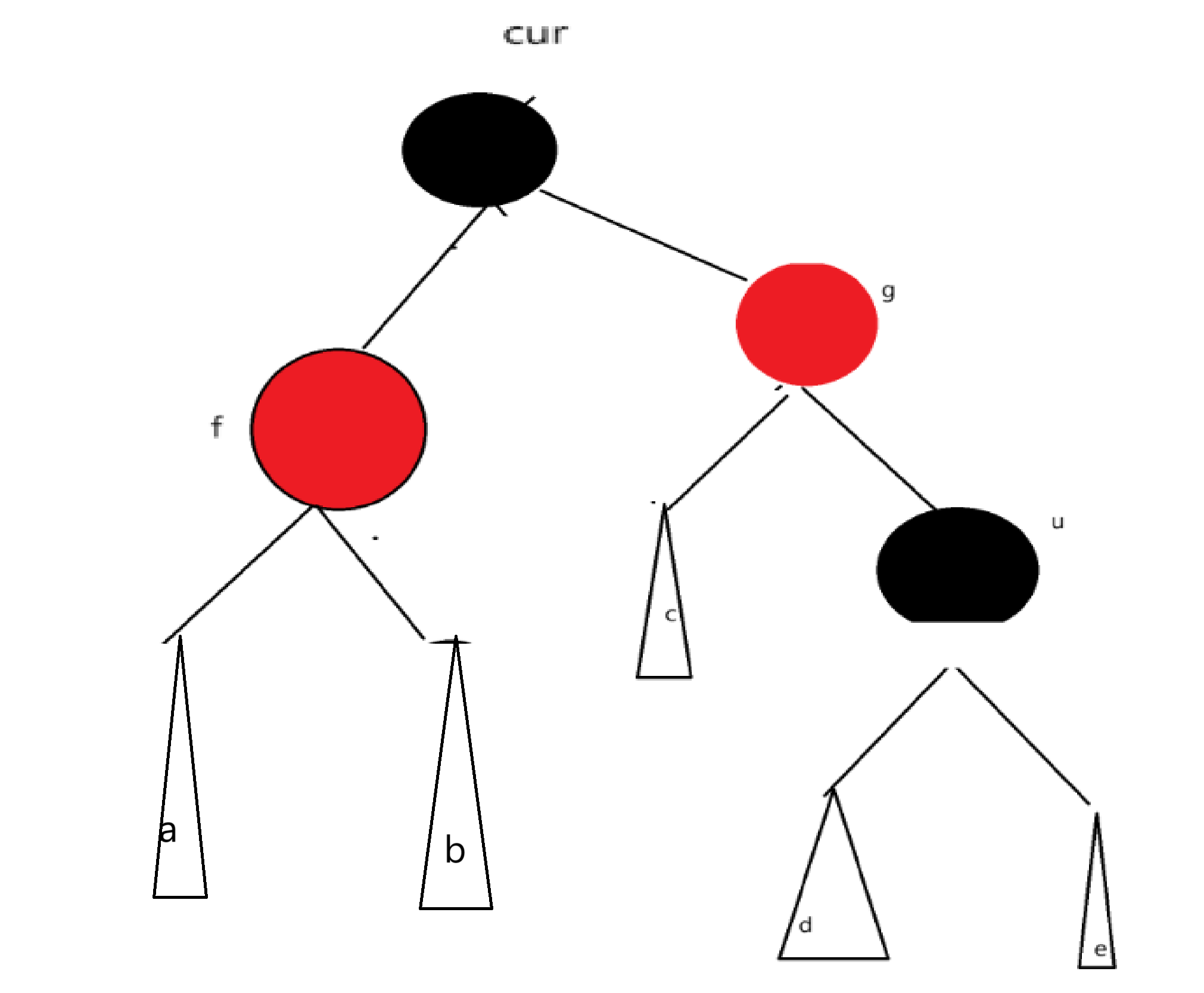u不存在，abcde都是空

u存在且为黑，abc都是一个黑色节点的红黑树，de是空或者红色节点

三、红黑树的实现

3.1旋转

void RoLeft(Node * parent)
{Node* SubR = parent->_right;Node* SubRL = SubR->_left;parent->_right = SubRL;SubR->_left = parent;if (SubRL)SubRL->_parent = parent;Node* parentParent = parent->_parent;parent->_parent = SubR;if (_root == parent){_root = SubR;SubR->_parent = nullptr;}else {if (parentParent->_left == parent){parentParent->_left = SubR;}else{parentParent->_right = SubR;}SubR->_parent = parentParent;}
}
void RoRight(Node * parent)
{Node* SubL = parent->_left;Node* SubLR = SubL->_right;SubL->_right = parent;parent->_left = SubLR;if (SubLR)SubLR->_parent = parent;Node* parentParent = parent->_parent;parent->_parent = SubL;if (_root == parent){_root = SubL;SubL->_parent = nullptr;}else{if (parentParent->_left == parent){parentParent->_left = SubL;}else{parentParent->_right = SubL;}SubL->_parent = parentParent;}
}

3.2插入

	bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = Black;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = Red;if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}while (parent&&parent->_col == Red){//      g//    p  u//  cNode* grandfather = parent->_parent;if(grandfather->_left==parent){Node* uncle = grandfather->_right;//叔叔存在且为红if (uncle && uncle->_col == Red){parent->_col = uncle->_col = Black;grandfather->_col = Red;cur = grandfather;parent = grandfather->_parent;}else{if (parent->_left == cur){//叔叔不存在或者叔叔存在且为黑RoRight(grandfather);parent->_col = Black;grandfather->_col = Red;}	//      g//    p  u//  celse{//叔叔不存在或者叔叔存在且为黑RoLeft(parent);RoRight(grandfather);cur->_col = Black;grandfather->_col = Red;}break;}}//      g//    u  p//       celse{Node* uncle = grandfather->_left;if (uncle && uncle->_col == Red){parent->_col = uncle->_col = Black;grandfather->_col = Red;cur = grandfather;parent = cur->_parent;}else {//      g//    u  p//       cif (parent->_right == cur){RoLeft(grandfather);grandfather->_col = Red;parent->_col = Black;}else{RoRight(parent);RoLeft(grandfather);grandfather->_col = Red;cur->_col = Black;}break;}}}_root->_col = Black;return true;}

void InOrder()
{_InOrder(_root);cout << endl;
}void _InOrder(Node* root)
{if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);
}

每一种情况我都有在上面做一点小标记，大家把我上面红黑树定义里面的情况都画出来，对照着写代码就可以了

3.3测试

int main()
{const int N = 30;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(rand());}RBtree<int, int> t;for (auto e : v){t.Insert(make_pair(e, e));}t.InOrder();return 0;
}

我在这里放随机数来测定，如果随机数测定成功了，那么静态数据也可以成功

还是和AVL树一样这里我们只能判断它是搜索树，不能判断它是红黑树

所以我们还要针对红黑树的规则来针对它写代码来测试它

针对规则三我们直接检查其实不好检查，因为孩子节点的情况太多了，两个孩子可以为空，为红等等

针对规则4我们可以考虑传值而不是传引用

我们使用传值的时候比如说2是1到1变2，但是返回上去到2的右还是1这样我们就能验证每条路径的黑色节点数量，那我们是否要记录下来呢，可以记录，把他们都放到一个数组vector里面去，或者我们可以更好地给出一个参考值，判断一下和这个参考值是否相等就行了

	bool IsBalance(){return _IsBalance(_root);}bool Check(Node* root,int blacknum,const int Referencevalue){if (root == nullptr){if (blacknum != Referencevalue){cout << "存在黑色节点数量不相等的路径" << endl;}return true;}if (root->_col == Red&&root->_parent->_col==Red){cout << "有连续的红色节点" << endl;return false;}if (root->_col == Black){++blacknum;}return Check(root->_left, blacknum, Referencevalue) && Check(root->_right, blacknum, Referencevalue);}bool _IsBalance(Node* root){if (root == nullptr)return false;if (root->_col == Red)return false;int blacknum = 0;int Referencevalue = 0;Node* cur = root;while (cur){if (cur->_col == Black)Referencevalue++;cur = cur->_left;}return Check(root, blacknum, Referencevalue);}

红黑树就写到这里了，接下来进入更难的封装，红黑树有了AVL树旋转做基础和铺垫学起来也会不那么复杂

一、红黑树的概念

二、红黑树的定义

三、红黑树的实现

相关文章：