当前位置：首页 > news >正文

【强化学习-蘑菇书-3】马尔可夫性质，马尔可夫链，马尔可夫过程，马尔可夫奖励过程，如何计算马尔可夫奖励过程里面的价值

news 来源：原创 2025/9/7 16:48:38

欢迎去各大电商平台选购纸质版蘑菇书《Easy RL：强化学习教程》

文章是根据蘑菇书EasyRL ，网络查找资料和汇总，以及新版本的python编写的可运行代码和示例，包含了一些自己对书内容的简单理解

一、马尔可夫性质

在随机过程中，马尔可夫性质（Markov property）是指一个随机过程在给定现在状态及所有过去状态情况下，其未来状态的条件概率分布仅依赖于当前状态。

举个例子：

明天的天气（是否下大雨）仅与今天的天气（是否刮大风）有关，而与前天及以前的天气无关

我今天醒来花呗剩余额度只和我昨天的额度及昨天的消费情况有关，跟历史数据没有关系。

The future is independent of the past given the present
未来独立于过去，只基于当下。

过去所有的信息都已经被保存到了现在的状态，基于现在就可以预测未来。

如果某一个过程满足马尔可夫性质，那么未来的转移与过去的是独立的，它只取决于现在。马尔可夫性质是所有马尔可夫过程的基础。

二、随机过程 :原文地址：https://zhuanlan.zhihu.com/p/448575579

马尔可夫链是随机过程 这门课程中的一部分，先来简单了解一下。

随机过程就是使用统计模型一些事物的过程进行预测和处理，比如股价预测通过今天股票的涨跌，却预测明天后天股票的涨跌；天气预报通过今天是否下雨，预测明天后天是否下雨。

这些过程都是可以通过数学公式进行量化计算的。通过下雨、股票涨跌的概率，用公式就可以推导出来 N 天后的状况。

天气预报通过今天是否下雨，预测明天后天是否下雨（的概率）：

股价预测通过今天股票的涨跌，却预测明天后天股票的涨跌（的概率）；

这个马尔可夫链是表示股市模型的，共有三种状态：牛市（Bull market）, 熊市（Bear market）和横盘（Stagnant market）。每一个状态都以一定的概率转化到下一个状态。比如，牛市以0.025的概率转化到横盘的状态。

这个状态概率转化图可以以矩阵的形式表示。如果我们定义矩阵P某一位置 $P (i, j)$ 的值为 $P (i ∣ j)$ ，即从状态i转化到状态j的概率，并定义牛市为状态0，熊市为状态1, 横盘为状态2。

这样我们得到了马尔科夫链模型的状态转移矩阵为：

$\begin{equation} %开始数学环境 P=\left( %左括号 \begin{array}{ccc} %该矩阵一共3列，每一列都居中放置 0.9 & 0.075 & 0.025\\ %第一行元素 0.15 & 0.8 & 0.05\\ %第二行元素 0.25 & 0.25 & 0.5\\ %第三行元素 \end{array} \right) %右括号 \end{equation}$

三、马尔科夫链

马尔可夫过程是一组具有马尔可夫性质的随机变量序列 s1,s2……，其中下一个时刻的状态s(t+1)只取决于s(t)，也就是上一时刻的状态（可以理解成：过去所有的信息都已经被保存到了现在的状态，基于现在就可以预测未来。）

从当前 s(t)，转移到 s(t+1),它是直接就等于它之前所有的状态转移到 s(t+1)。

离散时间的马尔可夫过程也称为马尔可夫链（Markov chain）

马尔可夫链是最简单的马尔可夫过程，其状态是有限的，

例如，下图里，有4个状态，这4个状态在 S1,S2,S3,S4之间互相转移

S1有0.1的概率留在S1， 0.2的概率去S2， 0.7的概率去S4
S2只能转移到S1
S3只能转移到S2
S4有0.5概率留在S4， 0.2概率转移到S3，0.3概率转移到S2
在这里插入图片描述
我们可以用状态转移矩阵（state transition matrix）P来描述状态转移的关系，
也就是从
S1->S1,S1->S2,S1->S3,S1->S4
S2->S1,S2->S2,S2->S3,S2->S4
S3->S1,S3->S2,S3->S3,S3->S4
S4->S1,S4->S2,S4->S3,S4->S4

带入图中的例子得到状态转移矩阵

S1->S1（0.1）,S1->S2（0.2）,S1->S3（0.0）,S1->S4（0.7）
S2->S1（1.0）,S2->S2（0.0）,S2->S3（0.0）,S2->S4（0.0）
S3->S1（0.0）,S3->S2（1.0）,S3->S3（0.0）,S3->S4（0.0）
S4->S1（0.0）,S4->S2（0.3）,S4->S3（0.2）,S4->S4（0.5）

它的每一行描述的是从一个节点到达所有其他节点的概率。

四、马尔可夫过程的例子

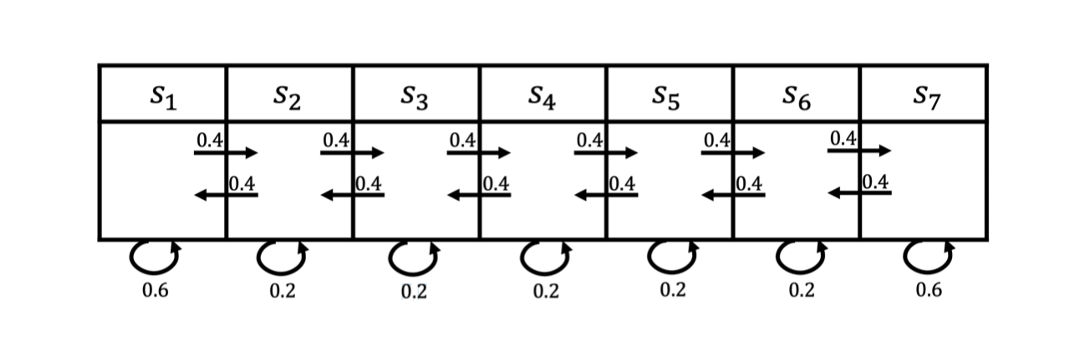
在这里插入图片描述
上图所示为一个马尔可夫过程的例子，这里有七个状态。

比如从 $s_1$ 开始，它有0.4的概率到 $s_2$ ，有 0.6 的概率留在当前的状态。
$s_2$ 有 0.4 的概率到 $s_1$ ，有 0.4 的概率到 $s_3$ ，另外有 0.2 的概率留在当前状态。

所以给定状态转移的马尔可夫链后，我们可以对这个链进行采样，这样就会得到一串轨迹。

例如，假设我们从状态 $s_3$ 开始，可以得到3个轨迹：

$s_3, s_4, s_5, s_6, s_6$ ；（ $s_6还可以去s_7,s_7又可以回到s_6，有很多的路径$ ）
$s_3, s_2, s_3, s_2, s_1$ ；
$s_3, s_4, s_4, s_5, s_5$ 。

这里只是列出了其中一些路径！！

通过对状态的采样，我们可以生成很多这样的轨迹。

例子2：

在这里插入图片描述
上图中有 A 和 B 两个状态，A 到 A 的概率是 0.3，A 到 B 的概率是 0.7；B 到 B 的概率是 0.1，B 到 A 的概率是 0.9。

初始状态在 A，如果我们求 2 次运动后状态还在 A 的概率是多少？非常简单：
$P=A\rightarrow A\rightarrow A +A\rightarrow B\rightarrow A$
其中
$A\rightarrow A\rightarrow A=0.3*0.3$

$A\rightarrow B\rightarrow A=0.7*0.9$

所以

$P = 0.3 * 0.3 + 0.7 * 0.9 = 0.72$

如果求 2 次运动后的状态概率分别是多少？初始状态和终止状态未知时怎么办呢？

这是就要引入转移概率矩阵 ，可以非常直观的描述所有的概率。

在这里插入图片描述

有了状态矩阵，我们可以轻松得出以下结论：

初始状态 A，2 次运动后状态为 A 的概率是 0.72；
初始状态 A，2 次运动后状态为 B 的概率是 0.28；
初始状态 B，2 次运动后状态为 A 的概率是 0.36；
初始状态 B，2 次运动后状态为 B 的概率是 0.64；

有了概率矩阵，即便求运动 n 次后的各种概率，也能非常方便求出。

状态转移矩阵的稳定性

状态转移矩阵有一个非常重要的特性，经过一定有限次数序列的转换，最终一定可以得到一个稳定的概率分布，且与初始状态概率分布无关。

更详细的信息在：

什么是马尔可夫链？：https://zhuanlan.zhihu.com/p/38764470

以上面的那个股市的例子来说：
假设我们当前股市的概率分布为： $[0.3, 0.4, 0.3]$ ，即30%概率的牛市，40%概率的熊盘与30%的横盘。然后这个状态作为序列概率分布的初始状态 $t 0$ ，将其带入这个状态转移矩阵计算 $t 1, t 2, t 3 \dots\dots$ 的状态。代码如下：

import numpy as np
matrix = np.matrix([[0.9, 0.075, 0.025],[0.15, 0.8, 0.05],[0.25, 0.25, 0.5]], dtype=float)
vector1 = np.matrix([[0.3, 0.4, 0.3]], dtype=float)for i in range(100):vector1 = vector1 * matrixprint('Courrent round: {}'.format(i+1))print(vector1)

可以发现，从第60轮开始，我们的状态概率分布就不变了，一直保持
，即62.5%的牛市，31.25%的熊市与6.25%的横盘。

那么这个是巧合吗？
我们现在换一个初始概率分布试一试，现在我们用 $[0.7, 0.1, 0.2]$ 作为初始概率分布，然后这个状态作为序列概率分布的初始状态 $t 0$ ，将其带入这个状态转移矩阵计算 $t 1, t 2, t 3 \dots\dots$ 的状态。代码如下：

import numpy as np
matrix = np.matrix([[0.9,0.075,0.025],[0.15,0.8,0.05],[0.25,0.25,0.5]], dtype=float)
vector1 = np.matrix([[0.7,0.1,0.2]], dtype=float)for i in range(100):vector1 = vector1*matrixprint('Current round: {}'.format(i+1))print(vector1)

可以看出，尽管这次我们采用了不同初始概率分布，最终状态的概率分布趋于同一个稳定的概率分布

也就是说我们的马尔可夫链模型的状态转移矩阵收敛到的稳定概率分布与我们的初始状态概率分布无关。

也就是说，如果我们得到了这个稳定概率分布对应的马尔可夫链模型的状态转移矩阵，则我们可以用任意的概率分布样本开始，带入马尔可夫链模型的状态转移矩阵，这样经过一些序列的转换，最终就可以得到符合对应稳定概率分布的样本。

这个性质不光对我们上面的状态转移矩阵有效，对于绝大多数的其他的马尔可夫链模型的状态转移矩阵也有效。同时不光是离散状态，连续状态时也成立。

五、马尔可夫奖励过程

1）非周期的马尔可夫链：

这个主要是指马尔可夫链的状态转化不是循环的，如果是循环的则永远不会收敛。幸运的是我们遇到的马尔可夫链一般都是非周期性的。

用数学方式表述则是：对于任意某一状态 $i$ ，d为集合 $n|n\geq1,P^n_{ii}>0$ 的最大公约数，如果 $d = 1$ ，则该状态为非周期的；

2）任何两个状态是连通的：

指的是从任意一个状态可以通过有限步到达其他的任意一个状态，不会出现条件概率一直为0导致不可达的情况；

3）马尔可夫链的状态数可以是有限的，也可以是无限的。

因此可以用于连续概率分布和离散概率分布；

4） $\pi$ 通常称为马尔可夫链的平稳分布。

在这里插入图片描述

马尔可夫奖励过程（Markov reward process, MRP）是马尔可夫链加上奖励函数。在马尔可夫奖励过程中，状态转移矩阵和状态都与马尔可夫链一样，只是多了奖励函数（reward function）。奖励函数 $R$ 是一个期望，表示当我们到达某一个状态的时候，可以获得多大的奖励。这里另外定义了折扣因子 $\gamma$ 。

折扣因子有以下的一些作用：

第一，有些马尔可夫过程是带环的，它并不会终结，我们想避免无穷的奖励。
第二，我们并不能建立完美的模拟环境的模型，我们对未来的评估不一定是准确的，我们不一定完全信任模型，因为这种不确定性，所以我们对未来的评估增加一个折扣。我们想把这个不确定性表示出来，希望尽可能快地得到奖励，而不是在未来某一个点得到奖励。
第三，如果奖励是有实际价值的，我们可能更希望立刻就得到奖励，而不是后面再得到奖励（现在的钱比以后的钱更有价值）。
第四：最后，我们也更想得到即时奖励。有些时候可以把折扣因子设为 0（ $\gamma=0$ ），我们就只关注当前的奖励。我们也可以把折扣因子设为 1（ $\gamma=1$ ），对未来的奖励并没有打折扣，未来获得的奖励与当前获得的奖励是一样的。折扣因子可以作为强化学习智能体的一个超参数（hyperparameter）来进行调整，通过调整折扣因子，我们可以得到不同动作的智能体。

六、如何计算马尔可夫奖励过程里面的价值

范围：范围（horizon） 是指一个回合的长度（每个回合最大的时间步数），它是由有限个步数决定的，例如在吃豆人里面，我们走XX步能吃到XX个豆子，这个步子不是无穷的，我们需要定义一个步数，决定吃豆人最多能走多少步。
回报：**回报（return）**可以定义为奖励的逐步叠加，假设时刻 $t$ 后的奖励序列为 $r_{t+1},r_{t+2},r_{t+3},\cdots$ ，则回报为
$G_{t}=r_{t+1}+\gamma r_{t+2}+\gamma^{2} r_{t+3}+\gamma^{3} r_{t+4}+\ldots+\gamma^{T-t-1} r_{T}$
其中， $T$ 是最终时刻， $\gamma$ 是折扣因子，越往后得到的奖励，折扣越多。这说明我们更希望得到现有的奖励，对未来的奖励要打折扣。

当我们有了回报之后，就可以定义状态的价值了，就是状态价值函数（state-value function）。对于马尔可夫奖励过程，状态价值函数被定义成回报的期望，即
$\begin{aligned} V^{t}(s) &=\mathbb{E}\left[G_{t} \mid s_{t}=s\right] \\ &=\mathbb{E}\left[r_{t+1}+\gamma r_{t+2}+\gamma^{2} r_{t+3}+\ldots+\gamma^{T-t-1} r_{T} \mid s_{t}=s\right] \end{aligned}$
其中， $G_t$ 是之前定义的折扣回报（discounted return）。我们对 $G_t$ 取了一个期望，期望就是从这个状态开始，我们可能获得多大的价值。所以期望也可以看成未来可能获得奖励的当前价值的表现，就是当我们进入某一个状态后，我们现在有多大的价值。

马尔可夫奖励过程

马尔可夫奖励过程依旧是状态转移，其奖励函数可以定义为：
智能体进入第一个状态 $s_1$ 的时候会得到 5 的奖励，
进入第七个状态 $s_7$ 的时候会得到 10 的奖励，
进入其他状态都没有奖励。
我们可以用向量来表示奖励函数，即 $\boldsymbol{R}=[5,0,0,0,0,0,10]$
在这里插入图片描述

图 2.4 马尔可夫奖励过程的例子

我们对 4 步的回合（ $\gamma=0.5$ ）来采样回报 $G$ 。

（1） $s_{4}, s_{5}, s_{6}, s_{7} \text{的回报}: 0+0.5\times 0+0.25 \times 0+ 0.125\times 10=1.25$

（2） $s_{4}, s_{3}, s_{2}, s_{1} \text{的回报}: 0+0.5 \times 0+0.25\times 0+0.125 \times 5=0.625$

（3） $s_{4}, s_{5}, s_{6}, s_{6} \text{的回报}: 0+0.5\times 0 +0.25 \times 0+0.125 \times 0=0$

我们现在可以计算每一个轨迹得到的奖励，

比如我们对轨迹 $s_4,s_5,s_6,s_7$ 的奖励进行计算，这里折扣因子是 0.5。在 $s_4$ 的时候，奖励为0。下一个状态 $s_5$ 的时候，因为我们已经到了下一步，所以要把 $s_5$ 进行折扣， $s_5$ 的奖励也是0。然后是 $s_6$ ，奖励也是0，折扣因子应该是0.25。到达 $s_7$ 后，我们获得了一个奖励，但是因为状态 $s_7$ 的奖励是未来才获得的奖励，所以我们要对之进行3次折扣。最终这个轨迹的回报就是 1.25。类似地，我们可以得到其他轨迹的回报。

这里就引出了一个问题，当我们有了一些轨迹的实际回报时，怎么计算它的价值函数呢？

比如我们想知道 $s_4$ 的价值，即当我们进入 $s_4$ 后，它的价值到底如何？

一个可行的做法就是我们可以生成很多轨迹，然后把轨迹都叠加起来。

比如我们可以从 $s_4$ 开始，采样生成很多轨迹，把这些轨迹的回报都计算出来，然后将其取平均值作为我们进入 $s_4$ 的价值。这其实是一种计算价值函数的办法，也就是通过蒙特卡洛（Monte Carlo，MC）采样的方法计算 $s_4$ 的价值。