当前位置：首页 > news >正文

【C语言】浮点数在内存的储存

news 来源：原创 2025/9/18 5:33:28

前言：

在上章，了解了整数在内存中的储存，在本章节为大家继续讲解浮点数的储存，也是数据储存的最后一部分。

浮点数是计算机科学中一种重要的数据类型，用于表示实数。它能够表示非常大或非常小的数值，并且可以处理小数部分。然而，浮点数的存储方式与整数完全不同，其存储原理和特性也决定了浮点数在使用过程中存在特殊。

介绍：

浮点数的概念：

浮点数是一种用来表示实数的数据类型，其特点是小数点的位置可以浮动。

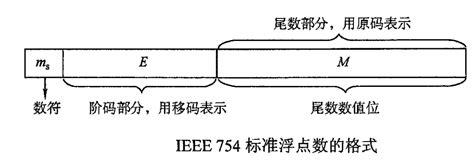
浮点数由三个部分组成：符号位（Sign）、指数位（Exponent）和尾数位（Mantissa）。符号位表示数值的正负，指数位表示数值的大小范围，尾数位则表示数值的具体精度。

浮点数的存储格式通常遵循IEEE 754标准，这是目前计算机系统中最常用的浮点数存储规范。IEEE 754标准定义了单精度浮点数（32位）和双精度浮点数（64位）两种主要格式。

常见的浮点数：3.1415926，1E10等，浮点数包含的类型有float，double，long double 浮点数的表示范围在头文件float.h中定义。

单/双精度

单精度浮点数（32位）
单精度浮点数由1位符号位、8位指数位和23位尾数位组成。具体存储方式如下：
- 符号位：1位，0表示正数，1表示负数。
- 指数位：8位，采用偏移量为127的二进制补码形式存储。
- 尾数位：23位，实际存储时省略了最高位的隐含1（即实际存储23位，但计算时加上隐含的1），这样可以节省存储空间。
双精度浮点数（64位）
双精度浮点数由1位符号位、11位指数位和52位尾数位组成：
- 符号位：1位，0表示正数，1表示负数。
- 指数位：11位，采用偏移量为1023的二进制补码形式存储。
- 尾数位：52位，同样省略了最高位的隐含1。

计组_浮点数表示/补码运算:定点数加减法/浮点数加减法(步骤+实例)「建议收藏」 - 全栈程序员必看

浮点数的范围与精度

范围
根据IEEE 754标准，单精度浮点数可以表示的数值范围为：
2^-126∼2^127

双精度浮点数的范围更广，可以表示更大的数值。

储存的原理

根据国际标准IEEE（电气和电子工程协会） 754，任意一个二进制浮点数V可以表示成下面的形式：

V = (-1)^S * M * 2^E

(-1)^S表示符号位，当S=0，V为正数；

当S=1，V为负数。

M表示有效数字，大于等于1，小于2。

2^E表示指数位。

举例：

十进制的5.0，写成二进制是 101.0 ，相当于 1.01×2^2 因为是二进制所以 底数是2，小数点向左移动了俩位所以指数是2 那么，按照上面V的格式，可以得出 S=0，M=1.01，E=2。

十进制的-5.0，写成二进制是 -101.0 ，相当于 -1.01×2^2，那么，S=1，M=1.01，E=2

在IEEE 754规定： 对于32位的浮点数，最高的1位是符号位S，接着的 8位是指数E，剩下的23位为有效数字M。

如图所示：

对于64位的浮点数，最高的1位是符号位S，接着的11位是指数E，剩下的52位为有效数字M。

有效数字M和指数E的特别规定

IEEE 754对有效数字M和指数E，还有一些特别规定

前面说过， 1≤M<2 ，也就是说，M可以写成 1.xxxxxx 的形式，其中xxxxxx表示小数部分。
IEEE 754规定，在计算机内部保存M时，默认这个数的第一位总是1，因此可以被舍去，只保存后面的xxxxxx部分。
比如保存1.01的时候，只保存01，等到读取的时候，再把第一位的1加上去。这样做的目的，是节省1位有效数字。
以32位浮点数为例，留给M只有23位，将第一位的1舍去以后，等于可以保存24位有效数字。

至于指数E，情况就比较复杂。

首先，E为一个无符号整数（unsigned int）

这意味着，如果E为8位，它的取值范围为0 ~ 255；
如果E为11位，它的取值范围为0 ~ 2047。但是，我们知道，科学计数法中的E是可以出现负数的。
所以IEEE 754规定，存入内存时E的真实值必须再加上一个中间数，对于8位的E，这个中间数是 127；
对于11位的E，这个中间数是 1023 。

比如，2^10的E是10，所以保存成32位浮点数时，必须保存成10+127=137，即 10001001。

取出原理

指数E的三种情况

（1） E不全为0或不全为1

这时，浮点数就采用下面的规则表示:

即指数E的计算值减去127（或1023），得到真实值，再将有效数字M前加上第一位的1。

比如：

0.5（1/2）的二进制形式为0.1，由于规定正数部分必须为1，即将小数点右移1位，则为
1.0*2^(-1)，其阶码为 -1+127=126，表示为 01111110，
而尾数1.0去掉整数部分为0，补齐0到23位 00000000000000000000000。所以 S=0 E=126 M=0 参考前面浮点数的储存模型可知则其二进制表示形式为:

0 01111110 00000000000000000000000

（2）E全为0

这时，浮点数的指数E等于1-127（或者1-1023）即为真实值。

有效数字M不再加上第一位的1，而是还原为0.xxxxxx的小数。这样做是为了表示±0，以及无限接近于0的很小的数字。

（3）E全为1

这时，如果有效数字M全为0，表示±无穷大（正负取决于符号位s)

例题

大家可以计算一下输出结果

#include <stdio.h>
int main()
{int n = 9;float* pFloat = (float*)&n;printf("n的值为：%d\n", n);printf("*pFloat的值为：%f\n", *pFloat);*pFloat = 9.0;printf("num的值为：%d\n", n);printf("*pFloat的值为：%f\n", *pFloat);return 0;
}

欧克，结果如下：

我猜部分帅哥，美女的结果都是：9 9.000000 9 9.000000

这是为什么呢？接下来只要好好思考一下浮点数的存储方式大家就明白了。

第一个简单：

n是 int类型，所以我们输出是以整形格式取出然后以%d十进制方式打印。

printf(“*pFloat的值为：%f\n”, *pFloat); 这个的话上难度了。

这个是对float类型的指针解引用但他指向地址是个整形而整形类型的在计算机存储的是补码：

9转成二进制就是 00000000000000000000000000001001

而按浮点数类型拿出的话 S=0 E=0 M= 0…1010

这里就是指数E为0的时候 套用浮点数计算公式 V = (-1)^S * M * 2^E

我们拿出的是一个无限接近0的一个小数而%f只打印6个零就不打印了所以我们打印的是： 0.000000

*pFloat = 9.0; printf(“num的值为：%d\n”, n);

这个打印为什么是1091567616

这段代码第一句话向指针指向的地址存进去了一个浮点数9.0

而浮点数的存储9.0 二进制是1001 写成科学计数法是 1.001

所以S=0 M=1.001 E=130 所以在内存存的是： 0 10000010 00100000000000000000000 转成十进制打印就是1091567616

*pFloat = 9.0;

*pFloat的值为：%f\n",

*pFloat这个是以浮点数的形式打印，而我们存进去的就是浮点数所以打印还是9.0

总结：

本章讲解了浮点数的概念；

存取原理；

希望对大家有所帮助。

有所帮助的话，关注一手把，我们下章再见！！！！

【C语言】浮点数在内存的储存

前言： 在上章，了解了整数在内存中的储存，在本章节为大家继续讲解浮点数的储存，也是数据储存的最后一部分。浮点数是计算机科学中一种重要的数据类型，用于表示实数。它能够表示非常大或非常小的数值，并且…...

编程日记 2025/9/18 5:33:28

安装 Calico 的两种主流方式对比

本文对比了 Calico 的两种主流安装方式： 使用 calico.yaml 的 Manifest 安装方式使用 Tigera Operator（tigera-operator.yaml custom-resources.yaml）安装方式 ✅ 1. 使用 Manifest 方式安装（直接部署 calico.yaml） …...

编程日记 2025/9/18 5:33:01

信用卡欺诈检测实战教程：从数据预处理到模型优化全解析

引言：为什么需要信用卡欺诈检测？ 根据尼尔森报告，全球每年因信用卡欺诈造成的损失超过250亿美元，金融机构需要在0.1秒内完成交易风险评估。本文将带您从零构建基于机器学习的信用卡欺诈检测系统，完整代码可视化分析&a…...

编程日记 2025/9/18 5:31:03

android studio 提示 Could not install Gradle distribution from https://services.gradle.org/distributions/gradle-8.0.2-bin.zip. Reason: java.net.SocketTimeoutException: Read timed out 一，手动下载 https://services.gradle.org/distributions/gradle…...

编程日记 2025/9/18 5:31:00

【Nodebb系列】Nodebb笔记写入方案

NodeBB写入方案前言最近在整理以前记录的碎片笔记，想把它们汇总到NodeBB中，方便管理和浏览。但是笔记内容有点多，并且用发帖的形式写到NodeBB中会丢失时间信息，因此整理了一套NodeBB写入方案，大致流程如下：建立标准笔记格式导出原始笔记，并编写脚本将笔记内容转换为…...

编程日记 2025/9/18 5:31:26

Spring Boot 集成 POI

Spring Boot 集合 POI Apache POI 官站：https://poi.apache.org/ 基础概念 Apache POI 是一个开源项目，提供 Java API 用于操作 Microsoft Office 文件格式。Apache POI 对 Excel 文件的处理分为两个主要类库： HSSF (Horrible Spreadsheet …...

编程日记 2025/9/10 3:09:36

8个方向使用DeepSeek打磨完美课题申报书！

一份出色的课题申报书，往往就是项目获批的关键。撰写高质量课题申报书绝非易事，它需要您在选题切入点、研究价值论证、技术路线设计、团队优势呈现、经费规划和预期成果等多维度进行精心布局，确保论证有力、重点突出、结构清晰。本文为您提供…...

编程日记 2025/9/7 18:53:42

Leetcode 34.在排序数组中查找元素的第一个和最后一个位置

题目描述给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值 target，返回 [-1, -1]。你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。考察二…...

编程日记 2025/9/18 5:31:28

ctfshow VIP题目限免密码逻辑脆弱

根据题目提示：公开的信息比如邮箱，可能造成信息泄露，产生严重后果在页面上找一个邮箱号从 QQ 上面搜索这个 QQ号，发现是一个叫大牛的人，地区是陕西西安然后我们拼接访问 /admin 发现了一个后台登录系统的页面&…...

编程日记 2025/9/18 5:33:28

C++初级入门学习

数据结构初级部分的学习我们已经学完了，接下来就进入C初阶部分的学习，因为数据结构的高阶部分要用到C才能够更好的理解并书写，所以我们要先学习C，初阶部分学完就能继续学习我们对数据结构了。好了，直接进入今天的主题吧…...

编程日记 2025/9/13 10:19:52

2025年汽车加气站操作工证考试内容

汽车加气站操作工证是从事汽车加气站相关操作工作的人员需要考取的资格证书考试内容理论知识：包括加气站的工艺流程、设备原理、安全操作规程、气体性质、消防知识、环境保护等方面的知识。例如，需要了解压缩天然气或液化天然气的储存、运输和加注流…...

编程日记 2025/9/16 13:41:18

python爬虫：喜马拉雅案例（破解sign值）

声明： 本文章中所有内容仅供学习交流使用，不用于其他任何目的，不提供完整代码，抓包内容、敏感网址、数据接口等均已做脱敏处理，严禁用于商业用途和非法用途，否则由此产生的一切后果均与作者无关&#xff…...

编程日记 2025/9/18 5:33:00

嵌入式AI前沿：精选工具与应用网站解析

1. Edge Impulse 网址：https://www.edgeimpulse.com/核心内容： 提供端到端的嵌入式AI开发平台，简化从数据收集到模型训练再到部署的全流程。支持多模态数据处理（音频、视觉、运动等），并优化模型以在资源受…...

编程日记 2025/9/18 5:31:28

【论文精读】Multi-scale Neighbourhood Feature Interaction Network

摘要（ABSTRACT） 光伏发电是工业领域的关键组成部分，其能量转换效率受光伏电池表面缺陷的显著影响。近年来，深度学习模型的广泛应用推动了缺陷检测技术的进步。然而，由于光伏电池缺陷尺寸差异较大（尤其是微…...

编程日记 2025/9/12 9:12:54

C++ 蓝桥云课代码练习

代码一 ，小明的背包1，代码见下 #include <iostream> #include <cstring> using namespace std;#define maxn 110 #define maxm 1001 #define inf -1int w[maxn], v[maxn]; int dp[maxn][maxm];int main() {memset(dp, inf, sizeof(dp));dp[…...

编程日记 2025/9/18 5:31:29

微软庆祝它成立整整50周年

每周跟踪AI热点新闻动向和震撼发展想要探索生成式人工智能的前沿进展吗？订阅我们的简报，深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同，从行业内部的深度分析和实用指南中受益。不要错过这个机会，成为AI领…...

编程日记 2025/9/18 5:30:59

android 启动四大组件

在 Android 开发中，启动通常是指启动一个 Activity、Service、BroadcastReceiver 或其他组件。以下是一些常见的启动方式： 1. 启动一个 Activity 要启动一个 Activity，可以使用 Intent。以下是一个示例代码： 示例：启…...

编程日记 2025/9/10 10:48:37

C# 串口通信

1. 导入 using System.IO.Ports;2. 初始化定义 SerialPort sp new SerialPort(); // 设置串口 sp.PortName "COM3"; // 串口 sp.BaudRate 9600; // 波特率 sp.Parity Parity.None; // 校验位 sp.DataBits 8; // 数据位 sp.StopBits StopBits.One; // 停…...

编程日记 2025/9/18 5:31:02

Spring事务详解

一、Spring对事务的支持 1.事务概述什么是事务在一个业务流程当中，通常需要多条DML（insert delete update）语句共同联合才能完成，这多条DML语句必须同时成功，或者同时失败，这样才能保证数据的安全。多…...

编程日记 2025/9/18 5:31:02

单片机FreeRTOSTickless低功耗模式应用示例

Tickless低功耗模式在很多需要延长电池寿命或减少能耗的场景中非常有用，特别是在那些大部分时间处于空闲状态的系统中。以下是一些使用Tickless模式的场景和例子： 1.传感器节点在物联网（IoT）中，许多传感器节点需要长…...

编程日记 2025/9/18 5:31:01

2025.4.9总结

今天周三，晚上默认不加班，每到闲暇的时候，总会瞎想。如今想想，是要多提升提升自身的软实力了。硬实力，是你的专业技能，是你吃饭的东西，而软实力则体现在人际交往，表达能力等方面。…...

编程日记 2025/9/18 5:31:03

Ceph异地数据同步之-Cephfs异地同步复制

#作者：闫乾苓文章目录 1.核心原理2.部署步骤3.cephfs同步测试4.查看cephfs文件同步状态5.优化cephfs文件系统同步的时间间隔 1.核心原理 Cephfs异地同步基于CephFS-mirror，其工作原理是基于CephFS的快照功能和cephfs-mirror工具的异步复制机制。它通过…...

编程日记 2025/9/10 12:33:32

大数据专业学习路线

大数据专业学习路线目录基础知识核心技术进阶技能实战项目职业发展学习资源学习计划常见问题 1. 基础知识 1.1 编程语言 Python：大数据分析的基础语言基础语法和数据类型函数和模块面向对象编程文件操作和异常处理常用库：NumPy, Pandas, Matplot…...

编程日记 2025/9/9 21:15:23

每日文献（十）——Part two

今天从第四部分级联RCNN开始介绍。目录四、级联RCNN 4.1 级联边界框回归 4.2 级联检测五、实验结果 5.1 实现细节 5.1.1 基准工作 5.2 质量不匹配 5.3 与迭代bbox和积分损失的比较 5.4 消融实验 5.5 与最先进的方法对比 5.6 泛化能力 5.7 PASCAL VOC数据集结果…...

编程日记 2025/9/14 9:35:01

8.3.1 MenuStrip（菜单）控件

编程日记 2025/9/17 20:23:46

仿真每日一练 | ABAQUS子程序DLOAD

ABAQUS中用户子程序DLOAD可用于定义分布载荷幅值随坐标、时间、单元编号、积分点编号等的变化，该功能主要应用于定义复杂的载荷工况，今天给大家举一个简单的例子介绍其使用方式： 图1 模型认识回顾一下ABAQUS的有限元分析流程： 图…...

编程日记 2025/9/11 21:49:10

Kubernetes(k8s)-备份Etcd介绍

作者介绍：简历上没有一个精通的运维工程师。请点击上方的蓝色《运维小路》关注我，下面的思维导图也是预计更新的内容和当前进度(不定时更新)。我们上一章介绍了Docker基本情况，目前在规模较大的容器集群基本都是Kubernetes，但是K…...

编程日记 2025/9/10 11:01:34

[leetcode]求最大公约数和最小公倍数（gcd和lcm算法）

求最大公约数和最小公倍数 Coding : 使用C的库 #include<iostream> #include<algorithm> using namespace std; int main() { int a, b; cout << "cin a and b of gcd : "; cin >> a >> b; int res __gcd(a, b);…...

编程日记 2025/9/11 21:34:18

B-tree 的原理源码分析及应用场景等

B-tree（B树）是一种自平衡的多路搜索树，广泛用于文件系统、数据库索引、键值存储系统等对大规模数据的高效插入、查找和删除有高要求的场景。相比于二叉搜索树（BST），B-tree 可以减少磁盘I/O次数，…...

编程日记 2025/9/16 0:18:45

MySQL 中的聚簇索引和非聚簇索引有什么区别？

MySQL 中的聚簇索引和非聚簇索引有什么区别？ 1. 从不同存储引擎去考虑在MySIAM存储引擎中，索引和数据是分开存储的，包括主键索引在内的所有索引都是“非聚簇”的，每个索引的叶子节点存储的是数据记录的物理地址（指针…...

编程日记 2025/9/12 15:20:23

重构居家养老安全网：从 “被动响应” 到 “主动守护”

随着全球老龄化加剧，居家养老安全成为社会关注的核心议题。传统养老模式依赖人工巡检或单一传感器，存在响应滞后、隐私泄露、场景覆盖不足等问题。由此智绅科技应运而生，七彩喜智慧养老系统构筑居家养老安全网。而物联网（Io…...

编程日记 2025/9/4 13:45:36

从静态绑定驱动模型到现代设备模型 —— 一次驱动架构的进化之旅

🔍 B站相应的视屏教程： 📌 内核：博文视频 - 从静态绑定驱动模型到现代设备模型在 Linux 内核的发展历程中，设备驱动结构经历了从"硬编码手动注册"的早期实现方式，到"设备模型统一管理&qu…...

编程日记 2025/9/11 18:26:02

MySQL学习笔记十五

第十七章组合查询 17.1组合查询 MySQL允许执行多个查询（多条SELECT语句），并将结果作为单个查询结果集返回。这些组合查询通常称为并（union）或复合查询（compound query）。以下几种情况需要使…...

编程日记 2025/9/9 13:34:30

NLP基础知识与词向量的转化方法发展

目录 1.NLP 基础知识点为什么需要自然语言处理？自然语言处理有哪些分类？自然语言处理有哪些实际应用？为什么需要自然语言处理？自然语言处理有哪些分类？自然语言处理有哪些实际应用？自然语言处理的技术/工作原理是什么？ 2.NLP文本转化为词向量的方法 2…...

编程日记 2025/9/4 13:38:55

VectorBT量化入门系列：第四章高级策略开发与优化

VectorBT量化入门系列：第四章高级策略开发与优化本教程专为中高级开发者设计，系统讲解VectorBT技术在量化交易中的应用。通过结合Tushare数据源和TA-Lib技术指标，深度探索策略开发、回测优化与风险评估的核心方法。从数据获取到策略部署&am…...

编程日记 2025/9/14 5:55:49

JVM虚拟机篇（七）：JVM垃圾回收器全面解析与G1深度探秘及四种引用详解

JVM垃圾回收器全面解析与G1深度探秘及四种引用详解 JVM虚拟机（七）：JVM垃圾回收器全面解析与G1深度探秘及四种引用详解一、JVM有哪些垃圾回收器1. Serial回收器2. ParNew回收器3. Parallel Scavenge回收器4. Serial Old回收器5. Parallel Old回…...

编程日记 2025/9/11 0:56:34

【蓝桥杯】15届JAVA研究生组F回文字符串

一、思路 1.这题去年考的时候想的是使用全排列进行尝试，实际不用这么麻烦，只用找到第一个和最后一个非特殊字符串的位置，然后分别向内检查是否对称，向外检查是否对称直到左指针小于0(可以通过添加使其对称) 2.至于如何找到第一个…...

编程日记 2025/9/10 0:40:13

TDengine 语言连接器（Python ）

简介 taospy 是 TDengine 数据库面向 Python 语言提供的官方连接器，连接器对外提供对数据库写入、查询、订阅等多种访问接口。安装连接器命令如下： # 原生连接和 REST 连接 pip3 install taospy# WebSocket 连接，可选装 pip3 install tao…...

编程日记 2025/9/17 23:22:48

Android compose源码浅析——Modifier

Modifier浅析 Modifier的使用foldOutfoldInanyall总结Modifier的使用先来一段代码1： @Preview(showBackground = true) @Composable fun GreetingPreview() {ComposeTestTheme {Box(modifier = Modifier.size(DpSize(Dp(100f),Dp(100f))).padding(Dp(10f)).background(Colo…...

编程日记 2025/9/12 17:29:36

基于机器视觉的多孔零件边缘缺陷检测（源码C++、opencv、凸包、凸缺陷检测）

👑主页：吾名招财 👓简介：工科学硕，研究方向机器视觉，爱好较广泛… 💫签名：面朝大海，春暖花开！ 基于机器视觉的多孔零件边缘缺陷检测（源码C、ope…...

编程日记 2025/9/15 14:17:39

JAVAWeb_Servlet：前置准备与理论简易介绍

要写JAVA_Web：首先就得建个项目——如何在Eclipse新建一个Web项目-CSDN博客然后我们考虑具体的代码细节（接下来就是我们的前置准备） 一、导包： 在 Eclipse 中，如果需要快速导入缺失的包（例如&#xff0…...

编程日记 2025/9/15 11:37:22

反射 tcp

反射临时越过权限获取成员变量1并进行修改成员方法 TCP客户端...

编程日记 2025/8/18 0:45:23

UML综合实验四

1. 计算机包含内存(RAM)、CPU等硬件设备，根据下面的“产品等级结构-产品族”示意图，使用抽象工厂模式实现计算机设备创建过程并绘制相应的类图。 2. 电脑组装工厂可以将CPU、内存、硬盘、主机、显示器等硬件设备组装在一起构成一台完整的电脑&#xff0c…...

编程日记 2025/9/15 12:52:41

＜《AI大模型应知应会100篇》第8篇：大模型的知识获取方式及其局限性

第8篇：大模型的知识获取方式及其局限性摘要大模型（如GPT、BERT、Qwen、DeepSeek等）凭借其卓越的自然语言处理能力，已经成为人工智能领域的明星。然而，这些模型“知道”什么？它们如何获取知识&#xff1f…...

编程日记 2025/9/15 20:26:54

【回眸】Linux 内核 (十六) 之多线程编程下

前言前面介绍了互斥锁，本篇博文介绍死锁及其他多线程遇到的情况。什么情况会造成死锁死锁指的是两个或两个以上的运算单元（进程、线程或协程），互相持有对方所需的资源，导致它们都无法向前推进，从而导…...

编程日记 2025/9/17 16:18:05

学习笔记083——Java Stream API

文章目录 1、过滤数据 filter()2、转换元素 map()3、排序 sorted()3.1、自定义排序规则 4、去重 distinct()5、限制元素数量 limit()6、收集结果 collect()6.1、收集为List6.2、收集为Set6.3、转为Map6.4、基本用法（注意键冲突会抛异常）6.5、处理键冲突&…...

编程日记 2025/9/15 10:16:52

逍遥模拟器ARM过检测技术全解析

逍遥模拟器ARM框架安装magisk和修改设备型号隐藏应用隐藏root过检测逍遥模拟器ARMmagisk改设备型号隐藏应用隐藏root 引言逍遥模拟器以其出色的性能和丰富的功能，深受广大用户喜爱，让用户能在电脑上轻松运行各类安卓应用和游戏。然而，为保…...

编程日记 2025/9/14 1:32:28

Easysearch VS Opensearch 数据写入与存储性能对比

本文记录 Easysearch 和 Opensearch 数据写入和数据存储方面的性能对比。准备压测工具：INFINI Loadgen 对比版本： Easysearch 1.11.1（lucene 8.11.4）Opensearch 2.19.1（lucene 9.12.1） 节点 JVM 配置…...

编程日记 2025/9/14 16:15:26

C++中STL学习（一）——向量、栈、堆、集合

#include “bits/stdc.h” using namespace std; int main() { // -------------------- 1、向量vector：可以替换数组，不需要事先指定长度 // ------------------------- vector arr; // 构建int数组 vector arr1(100); // 构建初始长度100的int向量 ve…...

编程日记 2025/9/16 1:58:33

柑橘病虫害图像分类数据集OrangeFruitDataset-8600

文章目录 1. 前言2. 数据类别介绍3. 数据集地址 1. 前言柑橘，作为水果界的 “宠儿”，不仅以其酸甜可口的味道深受大众喜爱，更是在全球水果产业中占据着举足轻重的地位。无论是早餐中的一杯橙汁，还是下午茶里的柑橘甜点&#xff…...

编程日记 2025/9/15 1:38:41

前言：

介绍：