当前位置：首页 > news >正文

数据结构（一）KMP+滑动窗口+链表+栈+队列

news 来源：原创 2025/9/20 15:46:24

数据结构-链表

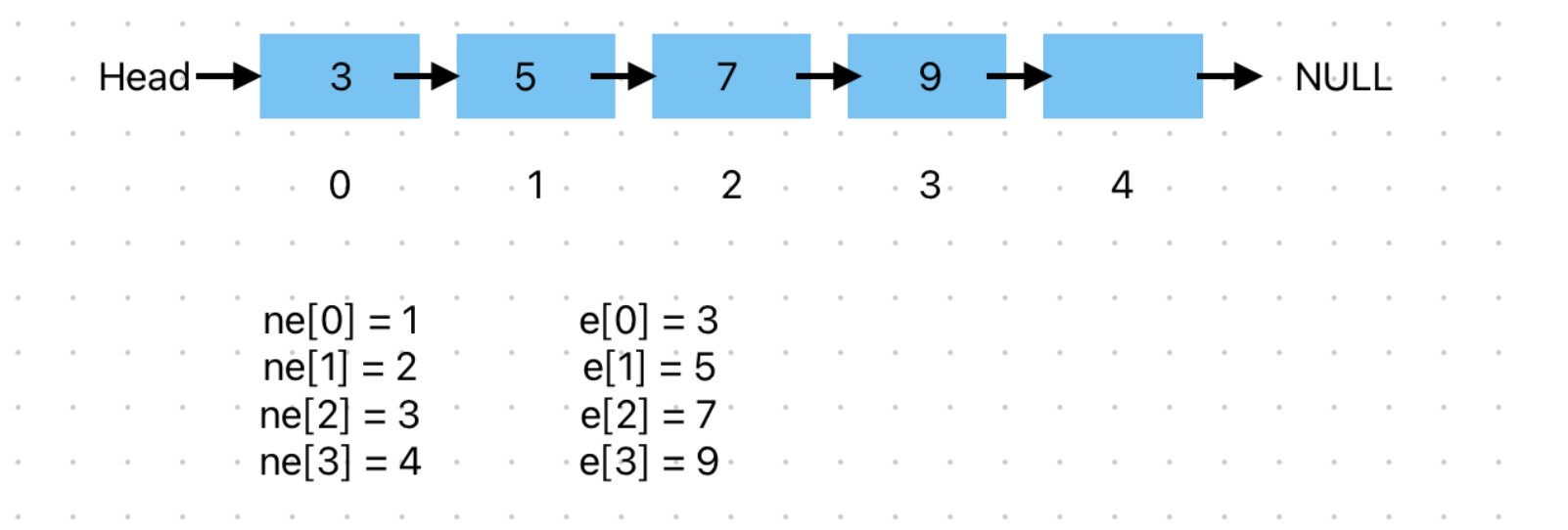
单链表

#include<iostream>
using namespace std;
const int N = 100010;

int head,e[N],ne[N],idx;

void init()
{head = -1;idx = 0;
}
void add_to_head(int x)
{e[idx] = x;ne[idx] = head;head = idx;idx++;
}
void add(int k,int x)
{e[idx] = x;ne[idx] = ne[k];ne[k] = idx;idx++;
}
void remove(int k)
{ne[k] = ne[ne[k]]; 
}
int main()
{int m;cin >> m;init();while(m--){int k,x;char op;cin >> op;if(op == 'H'){cin >> x;add_to_head(x);}else if(op == 'D'){cin >> k;if(k == 0) head = ne[head];else remove(k-1);}else{cin >> k >> x;add(k-1,x);}}for(int i = head;i!=-1;i=ne[i])cout << e[i] << ' ';cout << endl;return 0;
}

双链表

之所以在 “D”, “IL”, “IR” 要用 k+1 的原因是双链表的起始点是2. 所以，每个插入位置k的真实位置应该为 k-1+2 = k+1 (在单链表中为 k-1)。
0, 1 节点的作用是边界。0为左边界，1为右边界。他俩在这里有点类似保留字的作用。正因如此，我们的idx也是从2开始
最后遍历输出结果的 for (int i = rn[0]; i != 1; i = rn[i])。从 rn[0] 开始是因为 0 为左边界，而终止条件 i==1是因为1为右边界（如果碰到，说明已经遍历完毕）

#include<iostream>
using namespace std;

const int N = 100010;

int m;
int e[N],l[N],r[N],idx;

void insert(int a,int x)
{e[idx] = x;r[idx] = r[a];l[idx] = a;l[r[a]] = idx;r[a] = idx++;
}

void remove(int a)
{r[l[a]] = r[a];l[r[a]] = l[a];
}

int main()
{int m;cin >> m;r[0] = 1,l[1] = 0;idx = 2;while(m--){string op;cin >> op;int a,x;if(op == "L"){cin >> x;insert(0,x);}else if(op == "R"){cin >> x;insert(l[1],x);}else if(op == "D"){cin >> a;remove(a-1+2);}else if(op == "IL"){cin >> a >> x;insert(l[a+1],x);}else if(op == "IR"){cin >> a >> x;insert(a+1,x);}}for(int i = r[0];i!=1;i=r[i])cout << e[i] << ' ';cout << endl;return 0;
}

模拟栈（先进后出）

#include<iostream>
using namespace std;

const int N = 100010;
int m;
int stk[N],tt = 0;

int main()
{cin >> m;while(m--){string op;int x;cin >> op;if(op == "push"){cin >> x;stk[++ tt] = x;}else if(op == "pop")tt--;else if(op == "empty")cout << (tt ? "NO" : "YES") << endl;else cout << stk[tt] << endl;}return 0;
}

模拟队列（先进先出）

三木运算符

tt ? "NO" : "YES"

意思：如果 tt 为true 结果是 "NO"

如果 tt 是false 结果是"YES"，其中,在c++中,false 等价于0

#include<iostream>
using namespace std;

const int N = 100010;
int m;
int q[N],tt = -1,hh = 0;

int main()
{int m;cin >> m;while(m--){string op;cin >> op;int x;if(op == "push"){cin >> x;q[++tt] = x;}else if(op == "pop"){hh++;}else if(op == "empty") cout << (hh <= tt ? "NO" : "YES") << endl;else cout << q[hh] << endl;}return 0;
}

单调栈

暴力做法：两重循环。暴力求解

#include<iostream>
using namespace std;
const int N = 100010;
int stk[N],tt = 0;

int main()
{int n;cin >> n;while(n--){int x;cin >> x;//如果栈顶元素大于当前待入栈元素，则出栈while(tt && stk[tt] >= x)tt--;if(!tt)cout << "-1";else cout << stk[tt];stk[++tt] = x;}return 0;
}

//还有一种方法就是运用STL来做
#include<iostream>
#include<vector>
using namespace std;
int main()
{int n,x;cin >> n;vector<int> t;while(n--){cin >> x;while(t.size() > 0 and t.back() >= x){t.pop_back();}if(t.size() == 0){cout << -1 << ' ';}else cout << t.back() << ' ';
t.push_back(x);}return 0;
}

滑动窗口

//如果用普通队列的话
#include<iostream>
#include<queue>
using namespace std;

const int N = 1e6 + 10;
int a[N],n,k;

int main()
{cin >> n >> k;for(int i = 0;i<n;i++)  cin >> a[i];
//求每个窗口的最小值for(int i = 0;i<=n-k;++i){int minv = a[i];for(int j = i + 1;j < i + k;++j){minv  = min(minv,a[j]);}cout << minv << " ";}cout << endl;
//求每个窗口的最大值for(int i = 0;i <= n-k;++i){int maxv = a[i];for(int j = i + 1;j < i + k;++j){maxv = max(maxv,a[j]);}cout << maxv << " ";}cout << endl;
return 0;
}

如果运用单调队列的话，会超时

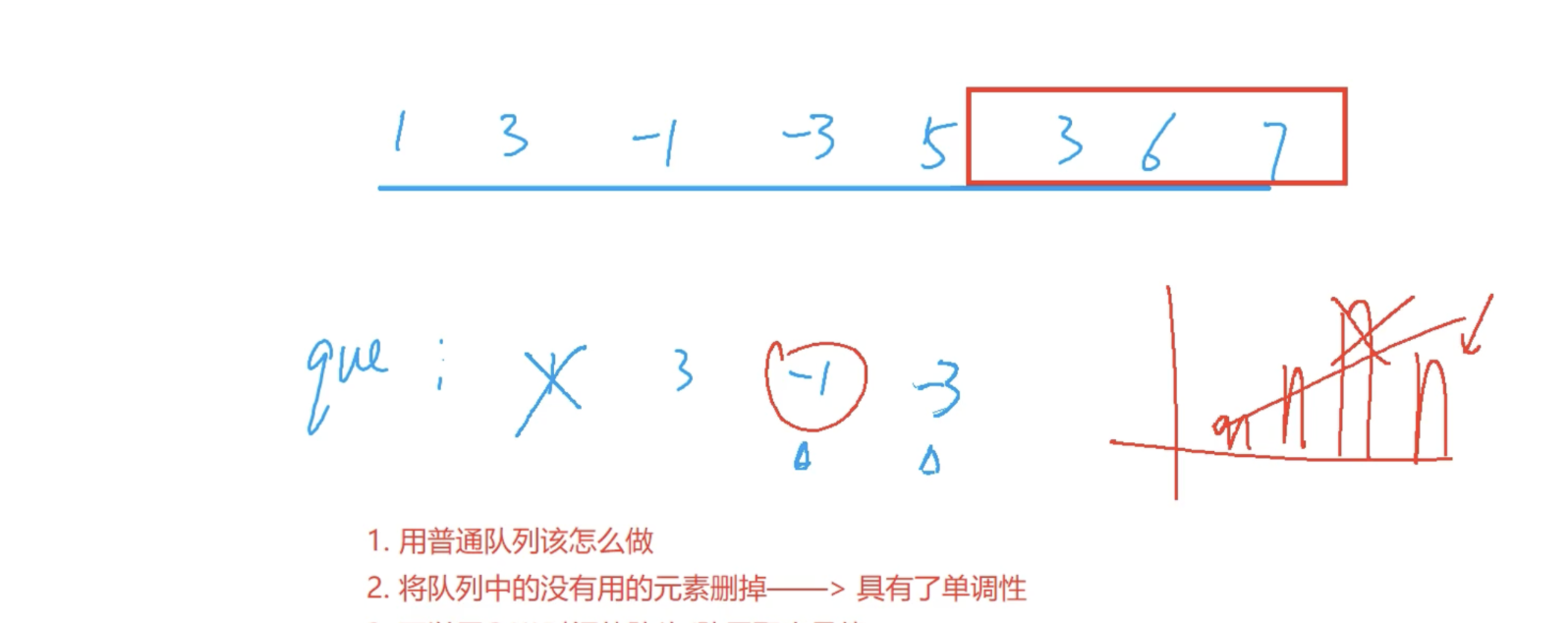
//运用双端队列
#include<iostream>
using namespace std;

const int N = 1000010;
//单调队列一般用双端队列保证其单调性.这里面的q数组表示下标，a数组表示数字
int a[N],q[N],n,k;
//队头与队尾，在队尾插入，在队头获取
int front = 0,tail = -1;
int main()
{scanf("%d%d",&n,&k);for(int i = 0;i<n;i++){scanf("%d",&a[i]);}//先找出这个窗口的最小值for(int i = 0;i < n;i++)
{if(front <= tail && i - k + 1 > q[front])front ++;while(front <= tail && a[i] <= a[q[tail]] ) tail--;//从队尾插入元素q[++tail] = i;//队头为窗口的最小值if(i >= k-1) printf("%d ",a[q[front]]);
}
printf("\n");//再找出这个窗口的最大值front = 0,tail = -1;for(int i = 0;i<n;i++){if(front <= tail && i - k + 1 > q[front])   front++;while(front <= tail && a[i] >= a[q[tail]]) tail--;q[++tail] = i;if(i >= k - 1) printf("%d ",a[q[front]]);}return 0;
}

KMP算法

暴力算法怎么做？如何去优化？

#include<iostream>
using namespace std;const int N = 100010,M = 1000010;
int n,m;
int ne[N];
char s[M],p[N];int main()
{cin >> n >> p + 1 >> m >> s + 1;//查找next数组进行一个匹配for(int i = 2,j = 0;i <= n;i++){while(j && p[i] != p[j + 1])   j = ne[j];if(p[i] == p[j+1])  j++;ne[i] = j;}//匹配操作for(int i = 1,j = 0;i <= m;i++){while(j && s[i] != p[j + 1]) j = ne[j];if(s[i] == p[j+1]) j++;if(j == n){printf("%d ",i - n);//j = ne[j];}}return 0;
}

这两张图片参考的acwing的四谷夕雨的

数据结构（一）KMP+滑动窗口+链表+栈+队列

数据结构-链表单链表 #include<iostream> using namespace std; const int N 100010; int head,e[N],ne[N],idx; void init() {head -1;idx 0; } void add_to_head(int x) {e[idx] x;ne[idx] head;head idx;idx; } void add(int k,int x) {e[idx] x;ne[id…...

编程日记 2025/9/20 15:46:24

C语言数据结构【队列】动态模拟实现

引言用动态方式模拟实现队列的各个接口一、队列的结构与概念概念：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出FIFO(First In First Out) 入队列：进行插入操作的一端称为队尾出队列…...

编程日记 2025/9/13 14:16:09

Python | 第十三章 | 多态 | 魔术方法 | 静态方法 | 抽象类

P130 多态练习题（1）2025/2/21 一、isinstance函数基本说明： isinstance()用于判断对象是否为某个类或其子类的对象基本语法:isinstance(object,classinfo)解读形参： object:对象 classinfo:可以是类名、基本类型或者由它们组成…...

编程日记 2025/9/10 15:16:46

线程安全问题的原因与解决方案总结

目录一什么是线程安全？ 二线程安全问题的实例三线程安全问题的原因 1.多个线程修改共享数据 2.抢占式执行 3.修改操作不是原子的 4.内存可见性问题 5.指令重排序四解决方案 1.同步代码块 2.同步方法 3.加锁lock解决问题一什么是线程安全&…...

编程日记 2025/9/20 6:55:50

设计模式-模版方法

目录什么是模版方法？ 怎么理解抽象类的算法骨架？ Burn功能骨架战士类法师类什么是模版方法？ 借助抽象类定义算法的骨架，再由具体子类实现算法的特定步骤。这种设计模式让算法的整体结构得以固定，同时又能让不…...

编程日记 2025/9/20 15:43:09

c# 运用策略模式与模板方法模式实例

策略模式策略模式的核心在于定义一系列算法，把它们封装起来，并且让它们能够相互替换。策略模式让算法的变化独立于使用算法的客户端。在这个方法里，策略模式的体现如下： convertFunc 参数：这是一个委托类型的参数&a…...

编程日记 2025/9/20 15:45:33

基于51单片机的3路温度报警器proteus仿真

地址： https://pan.baidu.com/s/1qrCpGuzZRbeFVVjaGMffQA 提取码：1234 仿真图： 芯片/模块的特点： AT89C52/AT89C51简介： AT89C51 是一款常用的 8 位单片机，由 Atmel 公司（现已被 Microchip 收…...

编程日记 2025/9/9 9:52:44

llama-factory微调qwen2.5-vl

本文不生产技术，只做技术的搬运工！！！前言目前大模型百花齐放，微调方法复杂多样，且教程复杂，工程端想要进行垂域模型适配困难重重，本篇博客详细介绍了qwen2.5-vl的全流程微调过程，包括环境配置、数据集制作、模型训练、模型导出、模型部署、模型推理等过程，希望对工…...

编程日记 2025/9/20 15:43:10

淘宝历史价格采集合规指南：官方 API + 轻量爬虫混合方案

在电商数据分析领域，获取淘宝商品的历史价格数据对于企业制定价格策略、进行竞品分析以及消费者洞察市场价格波动趋势都具有重要意义。然而，由于淘宝平台对数据安全和合规性的严格要求，历史价格采集工作需要在合法合规的框架内进行。本文将详…...

编程日记 2025/9/20 15:44:35

文档控件DevExpress Office File API v24.2亮点：不再支持非Windows系统

DevExpress Office File API是一个专为C#, VB.NET 和 ASP.NET等开发人员提供的非可视化.NET库。有了这个库，不用安装Microsoft Office，就可以完全自动处理Excel、Word等文档。开发人员使用一个非常易于操作的API就可以生成XLS, XLSx, DOC, DOCx, RTF, CS…...

编程日记 2025/9/11 10:09:33

TDengine.C/C++ 连接器

简介 C/C 开发人员可以使用 TDengine 的客户端驱动，即 C/C 连接器（以下都用 TDengine 客户端驱动表示），开发自己的应用来连接 TDengine 集群完成数据存储、查询以及其他功能。TDengine 客户端驱动的 API 类似于 MySQL 的 C API。…...

编程日记 2025/9/20 6:39:33

什么是混合搜索Hybrid Search？

🧠 向所有学习者致敬！ “学习不是装满一桶水，而是点燃一把火。” —— 叶芝我的博客主页： https://lizheng.blog.csdn.net 🌐 欢迎点击加入AI人工智能社区！ 🚀 让我们一起努力，共创AI未来！ 🚀 混合搜索通常指一种结合多种搜索方法或技术的搜索策略，旨在提供更…...

编程日记 2025/9/12 20:00:32

滤波器：模拟滤波器和数字滤波器的区别

滤波器是一种用于从信号中去除不需要的频率成分，只保留所需频率成分的电子设备或算法。根据实现方式的不同，滤波器主要分为模拟滤波器和数字滤波器两大类。以下是对这两种滤波器的详细比较： 一、实现方式与原理模拟滤波器实现方式&#xf…...

编程日记 2025/9/11 20:07:53

AudioRecord 录制pcm转wav

pcm转wav PCM 格式校验pcm 添加 wav 头信息WAVWAV 格式检验小端序？ 参考地址 PCM 格式校验 /*** 专业PCM文件验证（支持动态参数与多格式）* param silenceThreshold 静音检测阈值（0.0~1.0），默认90%零值为静…...

编程日记 2025/9/8 20:04:54

625SJBH网上便利店的设计与实现

1前言目前，网络正以一种前所未有的冲击力在影响着人类的活动，包括人类的生产和日常生活。网络的诞生和发展，颠覆了传统的信息传播方式，冲破了存在于传统交流方式中时间和空间的种种壁垒，极大地改变了人类从物质到精…...

编程日记 2025/9/18 12:15:24

如何开发英语在线训练小程序：从0到1的详细步骤

在数字化学习的浪潮下，英语在线训练小程序凭借便捷、高效的学习模式，成为众多英语学习者的得力助手。如果你也想开发一款独具特色的英语在线训练小程序，不妨参考以下步骤，开启你的小程序开发之旅。一、前期规划 （…...

编程日记 2025/9/16 3:26:13

java设计模式-装饰者模式

装饰者模式(Decorator) 定义 1、动态的将新功能附加到对象上，在对象功能扩展方面，他比继承更有弹性，也体现了开闭原则(OCP) 2、这里提到的动态的将新功能附加到对象和OCP原则，在后面应用实际上会以代码的形式体现。 //饮料 // 饮…...

编程日记 2025/9/19 17:36:10

我提了一个 Androidx IssueTracker

问题在运行 gradle plugin 插件的 transform R8 阶段出现了报错 Caused by: com.android.tools.r8.internal.xk: java.lang.NullPointerException: Cannot invoke “String.length()” because “” is null 报错日志 FAILURE: Build failed with an exception.* What went w…...

编程日记 2025/9/14 20:58:30

spring mvc @ResponseBody 注解转换为 JSON 的原理与实现详解

ResponseBody 注解转换为 JSON 的原理与实现详解 1. 核心作用 ResponseBody 是 Spring MVC 的一个注解，用于将方法返回的对象直接序列化为 HTTP 响应体（如 JSON 或 XML），而不是通过视图解析器渲染为视图（如 HTML&…...

编程日记 2025/9/10 18:23:27

RK3588芯片NPU的使用：Windows11 Docker中运行MobileNet模型以及部署到开发板进行目标检测

本文的目标本文将在RKNN Docker环境（见本系列的第二篇文章）中练习MobileNet图像分类示例，并通过adb工具部署到RK3588开发板。 MobileNet简介请参考上一篇文章。开发环境说明主机系统：Windows11目标设备：搭载RK35…...

编程日记 2025/9/6 14:20:19

智能仓储数字孪生Demo（Unity实现）

一、项目背景与行业痛点医药流通行业仓储管理面临三大核心挑战： 合规性风险：GSP（药品经营质量管理规范）对温湿度、药品批次追溯的严苛要求，传统人工记录易出错效率瓶颈：库区布局复杂，人工巡检…...

编程日记 2025/9/8 16:12:41

Qt上hook钩子的使用，监测键盘和鼠标。

演示平台：windows。编译环境：Qt5.12.2 MinGW 64-bit Windows API： ///加载钩子 /*** SetWindowsHookEx 函数解释* int idHook 所监控的挂钩类型* HOOKPROC lpfn 监控信息的处理函数* HINSTANCEhMod 监控信息的动态链接位置 nullptr则与本线…...

编程日记 2025/9/19 12:48:57

Android12源码编译之预置Android Studio项目Android.mk文件编写

1、在AndroidManifest.xml文件中添加package"com.sprd.silentinstalldemo"属性，因为新版本的Android Studio默认生成的AndroidManifest.xml是没有这个属性值的 <?xml version"1.0" encoding"utf-8"?> <manifest xmlns:an…...

编程日记 2025/9/18 22:44:26

微服务注册中心选择指南：Eureka vs Consul vs Zookeeper vs Nacos

文章目录引言微服务注册中心概述什么是服务注册与发现选择注册中心的标准常见的微服务注册中心1. Eureka1.1 理论基础1.2 特点1.3 示例代码 2. Consul2.1 理论基础2.2 特点2.3 示例代码 3. Zookeeper3.1 理论基础3.2 特点3.3 示例代码 4. Nacos4.1 理论基础4.2 特点4.3 示例代…...

编程日记 2025/9/18 15:48:57

pg_waldump无法定位WAL文件问题

目录排查pg_waldump无法定位WAL文件问题的步骤1. 确认WAL文件路径配置2. 检查WAL文件名格式3. 验证文件存在性4. 检查文件权限5. 时间线历史文件检查6. 使用pg_controldata验证状态7. 尝试指定完整路径典型错误场景及解决方案排查pg_waldump无法定位WAL文件问题的步骤 1. 确…...

编程日记 2025/9/12 11:14:03

Mysql安装

Mysql安装 1. windows安装1.1 官网下载1.2 安装 1. windows安装 1.1 官网下载官网下载选择对于版本，然后跳转到下载页 1.2 安装...

编程日记 2025/8/17 22:00:18

Windows版-RabbitMQ自动化部署

一键完成Erlang环境变量配置（ERLANG_HOME系统变量）‌ 一键完成RabbitMQ环境变量配置（RabbitMQ系统变量）‌ 实现快速安装部署RabbitMQ PS： 需提前下载安装： - otp_win64_25.0.exe (Erlang) - rabbit…...

编程日记 2025/9/13 2:03:57

spring mvc的拦截器HandlerInterceptor 接口详解

HandlerInterceptor 接口详解 1. 接口方法说明方法作用执行时机返回值/注意事项preHandle请求处理前拦截在控制器方法执行前调用返回 false 中断后续流程；返回 true 继续执行postHandle控制器方法执行后拦截在控制器方法返回结果后，视图渲染前调用无返…...

编程日记 2025/9/16 7:56:01

Linux平台内存泄漏检测工具介绍: ASan vs Valgrind

目录： 前言Valgrind 介绍在Ubuntu上安装Valgrind 核心主要功能Valgrind 基本用法1. --leak-checkfull2. --show-leak-kindsall3. --track-originsyes4. 其他常用选项--tool<name>--log-file<filename>-v / --verbose--error-exitcode<n> 示例命令…...

编程日记 2025/9/18 20:15:34

c# 数据结构链表篇有关单链表的一切

本人能力有限,本文仅作学习交流与参考,如有不足还请斧正目录 0.单链表好处 0.5.单链表分类 1.无虚拟头节点情况图示: 代码: 头插/尾插删除搜索遍历全部测试代码: 全部代码 2.有尾指针情况尾插全部代码 3.有虚拟头节点情况全部代码 4.循环单链表几个…...

编程日记 2025/9/15 2:04:11

二叉树层平均值：层序遍历+队列解法详解

给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。示例 1： 输入：root [3,9,20,null,null,15,7] 输出：[3.00000,14.50000,11.00000] 解释：第 0 层的平均值为 …...

编程日记 2025/9/9 3:58:52

解决 Docker Swarm 集群节点故障：从问题剖析到修复实战

解决 Docker Swarm 集群节点故障：从问题剖析到修复实战在使用 Docker Swarm 构建容器编排集群时，可能会遭遇各种难题。本文将分享一次处理 Docker Swarm 集群节点故障的实战经历，涵盖问题出现的缘由、详细剖析以及完整的解决步骤&#xff0…...

编程日记 2025/8/22 4:36:07

【Java中级】11章、注解、元注解介绍、快速入门，了解java注解的基本使用方式【2】

文章内容 JDK内置的基本注释类型 Override DeprecatedSuppressWarnings 元注解对注释进行注解 ❤️内容涉及注解的定义，快速入门，注意事项 🌈 跟着B站一位老师学习的内部类内容，现写这篇文章为学习内部类的小伙伴提供思路支持&…...

编程日记 2025/9/19 3:27:31

Qt中自定义插件和库(1)

Qt中自定义插件和库(1) 在Qt中自定义插件和库的方法有两种： 1.提升法。 2.自定义Qt Designer 插件法。下面就以《Qt 5.9 C开发指南》一书中的例子来讲解。下面先讲提升法。一、提升法提升法(Promotion)是Qt Designer中重用自定义控件的一种方法&#xff0c…...

编程日记 2025/9/18 15:20:02

RK3568下QT实现视频播放器

在开发多媒体应用时，视频播放器是常见的项目。QT 作为一款跨平台的 C++ 应用程序开发框架，凭借丰富的类库和工具，让开发视频播放器变得简单。本文将介绍如何使用 QT 的QMediaPlayer和QVideoWidget类，实现一个简单的视频播放器，并逐步添加打开视频、播放、暂停、停止以及进…...

编程日记 2025/9/16 4:57:34

Shell脚本核心要点总结

刷题： Shell脚本核心要点总结一、Shell基础定义：Shell是用户与内核交互的接口，本质是多个指令的集合，需遵循逻辑关系。类型： 编译型语言（如C）：需编译器（如gcc&#xf…...

编程日记 2025/9/15 7:27:21

C++-FFmpeg-(5)-1-ffmpeg原理-ffmpeg编码接口-AVFrame-AVPacket-最简单demo

1.视频编码原理 2.FFMpeg编码接口和AVPacket结构体详解 2.1ffmpeg编码接口 -编码器上下文 2.2AVPacket结构体 2.3AVFrame结构体 3.视频播放最简单demo 3.1FFMpeg编码器获取和上下文打开 3.2视频帧创建和测试 1.视频编码原理 1.1 流程：像素格式转换-&…...

编程日记 2025/9/19 1:53:39

Opencv计算机视觉编程攻略-第十二节处理视频序列

视频由一系列图像构成，这些图像称为帧，帧是以固定时间间隔获取的（称为帧速率，通常用帧/秒表示，例如大疆无人机抽取每一帧），本文将介绍如何读取、处理和存储视频序列。如果从视频序列中提取出独立…...

编程日记 2025/9/12 17:23:41

浮点许可优化管理软件 - 智能许可管理专家

为什么选择浮点许可优化管理软件? 在当今数字化时代，企业软件许可支出持续攀升，如何实现许可资源的最优配置成为一大挑战。浮点许可优化管理软件通过先进的算法和自动化技术，帮助企业实现许可资源的精准管理和成本优化。革命性的智能化功能…...

编程日记 2025/9/13 9:19:44

Spring Boot接口返回Long类型的数据时丢失精度的全局处理

1、问题当实体类中的字段为Long类型时，通过Ajax请求返回给前段，在js中数据会丢失精度直接通过postman请求或通过浏览器请求，看下响应则不会丢失精度 2、处理方式 1、使用JsonSerialize注解 JsonSerialize(using ToStringSerializer.…...

编程日记 2025/9/15 18:39:40

量子计算入门：开启未来计算的次元之门

在科幻电影中，我们常看到“量子计算机”被描绘成无所不能的黑科技——破解密码、模拟宇宙、瞬间完成超算百年的任务。但现实中，量子计算究竟是什么？它真的能颠覆传统计算机吗？ 一、从“硬币”到“薛定谔的猫”：量子世界…...

编程日记 2025/9/18 20:32:16

学习日志37—基于变分量子电路的量子机器学习算法综述

基于变分量子电路的量子机器学习算法综述论文原链接参考：https://crad.ict.ac.cn/article/cstr/32373.14.issn1000-1239.202330979 这篇综述的核心内容是基于变分量子电路（VQCs）的量子机器学习算法的研究现状、应用进展以及面临的挑战和未…...

编程日记 2025/9/18 20:22:39

初入Web网页开发

1、网页哪些内容 1.1 三个核心文件的作用 index.html：网页的骨架，用HTML编写网页结构和内容。 script.js：网页的行为，用JavaScript实现交互功能（如按钮点击事件）。 styles.css：网页的外观&…...

编程日记 2025/9/16 0:52:26

Vue进行前端开发流程

一、创建vue项目创建vue项目：先进入要操作的目录下，注意本项目是用vue2开发的。 vue create vue项目名二、项目开发 1.创建项目结构 2.开发功能模块主入口App.vue <template><div class"boss-app"><Header /><m…...

编程日记 2025/9/11 3:39:02

【深度学习:实战篇】--PyTorch+Transformer谣言检测系统

任务：构建一个多模态谣言检测模型。数据集描述如下： 数据集包含以下模态： 谣言文本：谣言的核心文本信息。2. 配图：与谣言文本相关的图像数据；3. OCR 文本：可以通过 PaddleOCR 从配图中提取的…...

编程日记 2025/9/20 11:04:27

PostGreSQL/openGauss表膨胀处理

如果面试官问你，Oracle与PG/OG最大的区别是什么？你要是没回答出MVCC机制，表膨胀，那你多半挂了。在PG/OG数据库中，命令vacuum full，插件pg_repack用于处理表膨胀，但是别高兴得太早，如…...

编程日记 2025/9/16 9:43:50

视频融合平台EasyCVR搭建智慧粮仓系统：为粮仓管理赋能新优势

一、项目背景当前粮仓管理大多仍处于原始人力监管或初步信息化监管阶段。部分地区虽采用了简单的传感监测设备，仍需大量人力的配合，这不仅难以全面监控粮仓复杂的环境，还容易出现管理 “盲区”，无法实现精细化的管理。而一套先进…...

编程日记 2025/9/18 18:16:07

基于 Node.js 和 Spring Boot 的 RSA 加密登录实践

在当今的互联网应用开发中，用户数据的安全性至关重要。登录功能作为用户进入系统的第一道防线，其安全性更是不容忽视。本文将介绍一种基于 RSA 加密的登录方案，前端使用 Node.js 的 node-forge 库对密码进行公钥加密，后端使用 Spr…...

编程日记 2025/9/20 12:34:24

jupyter在Pycharm中遇到的一个问题

jupyter比较简洁，可以分块执行，下面显示结果，还能用Markdown写注释，总体来说来还是比较好用的。但是遇到了一个奇怪的问题，从一个py文件中导入一个函数，结果输出为None。但是如果直接把这个函数的内容复制…...

编程日记 2025/9/14 11:56:44

十二、buildroot系统 adb登录权限设置

4.6.4、adb权限设置 android-adbd 是 ADB（Android Debug Bridge）的守护进程，允许开发者远程访问和调试设备。它通常用于 Android 设备，但在嵌入式 Linux上，也可以用来提供远程 shell、文件传输和应用调试功能。 …...

编程日记 2025/9/18 12:22:31

单链表

双链表

模拟栈（先进后出）

模拟队列（先进先出）

三木运算符

单调栈

滑动窗口

KMP算法

相关文章：