当前位置： 首页 > news >正文

约瑟夫环的四种(数组,链表,递归,迭代)解决方案，与空间、时间复杂度分析

news 来源：原创 2025/9/9 4:31:01

以下方法均没有考虑结果集的空间与时间复杂度

1.数组解法

实现代码（未优化）

class Main {public static void main(String[] args){Scanner read = new Scanner(System.in);int n = read.nextInt();int m = read.nextInt();int[] people = new int[n]; // 初始化数组(0表示存活，1表示出局)int currentIndex = 0; // 当前指针int count = 0;        // 计数器int alive = n;        // 存活人数List<Integer> sequence = new ArrayList<>();// 用来输出出局顺序的，与算法无关
​while (alive > 0) {if (people[currentIndex] == 0) {count++;if (count == m) {people[currentIndex] = 1;       // 标记出局sequence.add(currentIndex + 1); // 记录编号（这里加一是因为编号是从1开始，而数组是从0开始）count = 0;                      // 重新计数alive--;}}currentIndex = (currentIndex + 1) % n; // 模拟环形移动}
​// 输出结果for (int i = 0; i < n; i++) {if (i != 0) {System.out.print(" ");}System.out.print(sequence.get(i));}}
}

这个算法就是使用程序来模拟现实实际运行的情况

思路

  • 使用数组标记人员状态（存活/出局）。

  • 通过循环遍历数组计数存活者，找到第 m 个存活者后标记为出局。

时间复杂度

  • 单次出局操作：需要遍历 m ~（m+n）个存活者(因为会遍历到已经出局的人)。

  • 总时间复杂度：需处理 n 次出局，每次遍历 m ~（m+n）次，总时间复杂度约为 O(n*m) ~ O(n*m+n²)。也就是 O(n²)，当m很大的时候（并没有规定m一定要小于n！！！），这个算法是很亏的。

空间复杂度

  • 数组需 O(n) 空间，总空间复杂度为 O(n)。

优化点

如果考虑到m很大的情况，这段代码就又可以优化了。

当m大于现存活人生时，会出现重复遍历的情况，下面举一个例子：

假设 n=5，m=7，存活人数初始为 5：

  1. 第一轮有效步数 7%5=2，第二个人出局（编号 2）。

  2. 存活人数变为 4，有效步数 7%4=3，第三个人出局（编号 5）。

  3. 存活人数变为 3，有效步数 7%3=1，第一个人出局（编号 1）。

  4. 存活人数变为 2，有效步数 7%2=1，下一个人出局（编号 3）。

  5. 最后剩下编号 4 的人，出局顺序为 2 5 1 3 4。

通过取余优化，避免了每次遍历完整的 m 次，显著提升了效率。

优化后数组解法

import java.util.*;
​
class Main {public static void main(String[] args) {Scanner read = new Scanner(System.in);int n = read.nextInt();int m = read.nextInt();int[] people = new int[n];int currentIndex = 0;int count = 0;int alive = n;List<Integer> sequence = new ArrayList<>();
​while (alive > 0) {// 计算有效步数（取余优化）int effectiveM = m % alive;if (effectiveM == 0) {effectiveM = alive;}
​if (people[currentIndex] == 0) {count++;if (count == effectiveM) { // 用有效步数代替原mpeople[currentIndex] = 1;sequence.add(currentIndex + 1);count = 0;alive--;}}currentIndex = (currentIndex + 1) % n;}
​// 输出结果for (int i = 0; i < n; i++) {if (i != 0) {System.out.print(" ");}System.out.print(sequence.get(i));}}
}

优化后的时间复杂度与空间复杂度

  • 单次出局操作：经过取余操作后，有效步数的范围在 1 ~ n 之间。

  • 总时间复杂度：仍需处理 n 次出局，每次遍历 1 ~ n 次，总时间复杂度在 O(n) ~ O(n²) 之间，平均来说仍属于平方阶

  • 空间复杂度 ：总空间复杂度为 O(n)

2.链表解法

实现代码

import java.util.*;
​
class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();LinkedList<Integer> list = new LinkedList<>();for (int i = 1; i <= n; i++) list.add(i);ArrayList<Integer> sequence = new ArrayList<>();int currentIndex = 0;
​while (!list.isEmpty()) {currentIndex = (currentIndex + m - 1) % list.size();sequence.add(list.remove(currentIndex));}
​// 输出结果for (int i = 0; i < n; i++) {if (i != 0) System.out.print(" ");System.out.print(sequence.get(i));}}
}

思路

  • 实际上和数组解法类似，都是使用程序直接模拟实际行为。

  • 和数组不同的是，数组是使用标记来判断是否存活，而链表会将出局人移出，可以减少运行到后面的遍历数量。

时间复杂度

  • 单次删除操作：LinkedList 的 remove(int index) 方法平均需要 O(n) 时间，但是n会随着链表的缩短而减小，最终减少到1，所以单次的删除操作的时间复杂度在 O(1) ~ O(n) 。

  • 总时间复杂度：和优化后的数组类似，进行 n 次删除操作，总时间复杂度为 O(n) ~ O(n²)，仍属于平方阶

空间复杂度

  • 链表和结果列表各需 O(n) 空间，总空间复杂度为 O(n)。

3.递归解法

参考笔记

实现代码

import java.util.*;
​
class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();List<Integer> sequence = new ArrayList<>();for (int i = 1; i <= n; i++) {sequence.add(dg(n, m, i) + 1); // 加一是因为编号从 1 开始}// 输出出局顺序for (int i = 0; i < n; i++) {if (i != 0) {System.out.print(" ");}System.out.print(sequence.get(i));}}
​// 递归函数，计算第 i 轮出局的人的编号public static int dg(int n, int m, int i) {if (i == 1) {// 当只剩一个人时，直接返回最后一个人的编号（从 0 开始，所以要减1）return Math.floorMod(m - 1,n) ;//可以看作（m-1+n）% n}// 递归计算上一轮的结果，并加上 M 后取模return (dg(n - 1, m, i - 1) + m) % n;}
}

思路

  • 这段代码的解法思路就是将每一次淘汰人员都看作第一次淘汰，即下标都是从0开始

  • 递归就是为了计算淘汰出的人员的 原始下标 是多少

    新一轮中的编号：（旧一轮中的编号 - M）% 剩余人数

    eg:m=3

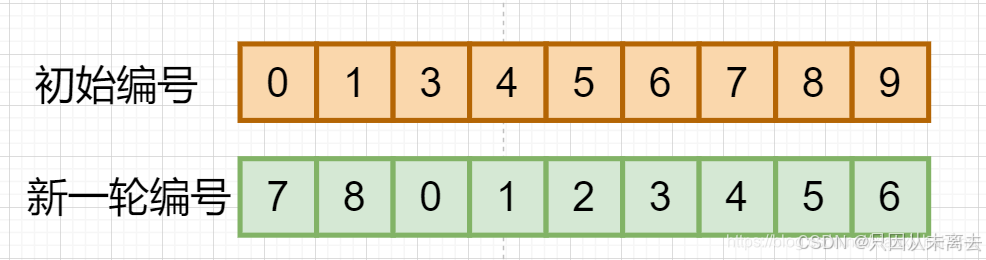
    因为每一次都从0开始数m个，所以将每一次的新一轮编号都减去m使其每次都是从0开始计数

    这时有人就要问了，我们在原本和谐的顺序中删除了一个2，不会使后续不连贯（少了个2，多了个9）吗？

    这就是这个 （旧一轮中的编号 - M）% 剩余人数 的妙处，他不仅能将需要约束在 0~（n-1）之间（因为淘汰了1人，9这个需要应该要剔除，最大值应该为8），还能将之前删掉的数据归入到n-1与0之间也就是8和0之间，这时候我们又能重新将其看成第一次在 n = 9，m=3 中淘汰玩家

    这就印证了递归解法的核心思路：

    • 每一次淘汰人员都看作第一次淘汰

    那么，旧一轮中的编号：（新一轮的编号 + M）% 剩余人数

    通过这个公式我们就能在每一层递归中保留上一层原始的下标

时间复杂度

  • 单次出局操作：每一次需要递归i层，i的值从1到n递增，所以单次时间复杂度在为 O(1)到O(n) 并为累加式

  • 总时间复杂度：需处理 n 次出局，每次遍历 1 ~ n 次，由等差数列求和公式可得总时间复杂度为
    O(1 + 2 + 3 + \ldots + n) = O\left(\frac{n(n+1)}{2}\right)

    也就是平方阶 O(n²) 而且会比较稳定。

    如果是只计算最终幸存人员的方式就为O(n)，因为他不需要像链表与数组一样依赖其他人的淘汰状态

空间复杂度

递归解法的主要空间开销来自于递归调用栈的深度。在每次递归调用 dg(n, m, i) 时，递归的深度为 i 层（例如，当计算第 i 轮出局时，需要递归 i 次）。由于主函数中对每个 i（从 1 到 n）都调用了一次递归函数，因此最大递归深度出现在计算最后一轮（i = n）时，此时递归深度为 n 层。

因此，空间复杂度为 O(n)，由递归调用栈的最大深度决定。

4.迭代解法

实现代码

import java.util.*;
​
class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();List<Integer> sequence = new ArrayList<>();
​for (int i = 1; i <= n; i++) {int current_k = n - i + 1; // 当前剩余人数int pos = (m - 1) % current_k; // 初始位置// 逐步计算在原始环中的位置for (int j = current_k + 1; j <= n; j++) {pos = (pos + m) % j;}sequence.add(pos + 1);}
​// 输出出局顺序for (int i = 0; i < n; i++) {if (i != 0) System.out.print(" ");System.out.print(sequence.get(i));}}
}

思路

  • 迭代解法和递归解法的思路是一致的，这种简单且深度固定的递归大多都能转化为某一公式的循环调用

  • 迭代解法其实是递归解法的优化版本，递归解法存在递归调用栈的开销，可能会导致栈溢出问题。而迭代解法通过循环的方式避免了递归调用栈的使用，直接从最底层的情况开始逐步向上计算，最终得到所需的结果。

  • 迭代解法同样基于递归解法中的核心递推公式： 旧一轮中的编号 = （新一轮的编号 + M） % 剩余人数

时间复杂度

  • 计算方式和递归方式一致

  • 单次出局操作：每一次计算需要循环 i 次，i 的值从 1 到 n 递增。

  • 总时间复杂度：需处理 n 次出局，每次遍历 1 ~ n 次，由等差数列求和公式可得总时间复杂度为O(1 + 2 + 3 + \ldots + n) = O\left(\frac{n(n + 1)}{2}\right)也就是平方阶 O(n²) ，

  • 同理如果是只计算最终幸存人员的方式就为O(n)

空间复杂度

  • 通过数学公式直接计算，避免了递归调用栈的开销，空间复杂度为 O(1) 在实际应用中比递归解法更加稳定，尤其是在处理大规模数据时。

相关文章：

约瑟夫环的四种(数组,链表,递归,迭代)解决方案，与空间、时间复杂度分析

以下方法均没有考虑结果集的空间与时间复杂度 1.数组解法 实现代码&#xff08;未优化&#xff09; class Main {public static void main(String[] args){Scanner read new Scanner(System.in);int n read.nextInt();int m read.nextInt();int[] people new int[n]; //…...

编程日记 2025/9/9 4:31:01

skynet.start 的作用详细解析

目录 skynet.start 的作用详细解析1. 功能概述2. 基本用法3. 关键作用(1) 注册消息处理函数(2) 启动事件循环(3) 服务生命周期管理 4. 与其他函数的协作5. 未调用 skynet.start 的后果6. 高级场景&#xff1a;何时不需要 skynet.start7. 总结 skynet.start 的作用详细解析 在 …...

编程日记 2025/9/8 5:09:59

Apache Doris 2025 Roadmap：构建 GenAI 时代实时高效统一的数据底座

在全球 290 位开发者的协作下&#xff0c;Apache Doris 在 2024 年完成了 7000 次代码提交&#xff0c;并发布了 22 个版本&#xff0c;实现在实时分析、湖仓一体和半结构化数据分析等核心场景的技术突破及创新。 2025 年&#xff0c;Apache Doris 社区将秉承“以场景驱动创新…...

编程日记 2025/9/3 7:05:57

springboot+easyexcel实现下载excels模板下拉选择

定义下拉注解 Target(ElementType.FIELD) Retention(RetentionPolicy.RUNTIME) public interface ExcelDropDown {/*** 固定下拉选项*/String[] source() default {};/*** 动态数据源key&#xff08;从上下文中获取&#xff09;*/String sourceMethod() default "";…...

编程日记 2025/9/9 3:53:12

vue3+ts+element-plus 开发一个页面模块的详细过程

目录、文件名均使用kebab-case&#xff08;短横线分隔式&#xff09;命名规范 子组件目录&#xff1a;./progress-ctrl/comps 1、新建页面文件 progress-ctrl.vue <script setup lang"ts" name"progress-ctrl"></script><template>&l…...

编程日记 2025/9/8 12:49:14

软考《信息系统运行管理员》- 7.1 物联网运维

物联网的概念及特征 物联网是在计算机互联网的基础上&#xff0c;通过射频识别 (RFID) 、 无线传感器、红外感应器、 全球定位系统、激光扫描器等信息传感设备&#xff0c;按约定的协议&#xff0c;把物与物之间通过网络连接起来&#xff0c; 进行信息交换和通信&#xff0c;以…...

编程日记 2025/9/6 10:42:32

【GPT入门】第33 课 一文吃透 LangChain：chain 结合 with_fallbacks ([]) 的实战指南

[TOC](【GPT入门】第33课 一文吃透 LangChain&#xff1a;chain 结合 with_fallbacks ([]) 的实战指南) 1. fallback概述 模型回退&#xff0c;可以设置在llm上&#xff0c;也可以设置在chain上&#xff0c;都带有with_fallbacks([])函数 2. llm的回退 2.1 代码 核心代码&…...

编程日记 2025/9/4 22:54:34

裴蜀定理：整数解的奥秘

裴蜀定理&#xff1a;整数解的奥秘 在数学的世界里&#xff0c;裴蜀定理&#xff08;Bzout’s Theorem&#xff09;是数论中一个非常重要的定理&#xff0c;它揭示了二次方程和整数解之间的关系。它不仅仅是纯粹的理论知识&#xff0c;还在计算机科学、密码学、算法优化等多个…...

编程日记 2025/9/8 16:39:00

Table as Thought论文精读

标题&#xff1a;Table as Thought: Exploring Structured Thoughts in LLM Reasoning 作者&#xff1a;Zhenjie Sun, Naihao Deng, Haofei Yu, Jiaxuan You 单位&#xff1a;University of Illinois Urbana-Champaign, University of Michigan 摘要&#xff1a; llm的推理…...

编程日记 2025/9/8 19:20:22

PyQt6实例_A股日数据维护工具_使用

目录 前置&#xff1a; 下载预备更新的数据 使用工具更新 用工具下载未复权、前复权、权息数据 在PostgreSQL添加两个数据表 工具&视频 前置&#xff1a; 1 本系列将以 “PyQt6实例_A股日数据维护工具” 开头放置在“PyQt6实例”专栏 2 日数据可在“数据库”专栏&…...

编程日记 2025/9/3 6:56:46

MySQL客户端工具-图形化工具-DataGrip 安装与使用

一. 常见的图形化工具 二. DataGrip 安装 官网&#xff1a;DataGrip&#xff1a;由 JetBrains 开发的数据库和 SQL 跨平台 IDE 二. DataGrip 使用...

编程日记 2025/9/7 1:29:57

企业管理系统的功能架构设计与实现

一、企业管理系统的核心功能模块 企业管理系统作为现代企业的中枢神经系统&#xff0c;涵盖了多个核心功能模块&#xff0c;以确保企业运营的顺畅与高效。这些功能模块通常包括&#xff1a; 人力资源管理模块&#xff1a;负责员工信息的录入、维护、查询及统计分析&#xff0c…...

编程日记 2025/9/4 9:17:36

1.Qt信号与槽

本篇主要介绍信号和槽&#xff0c;如何关联信号和槽以及用QPixmap在窗口中自适应显示图片 本文部分ppt、视频截图原链接&#xff1a;[萌马工作室的个人空间-萌马工作室个人主页-哔哩哔哩视频] 1. 信号 一般不需要主动发送信号&#xff0c;只有自定义的一些控件才需要做信号的…...

编程日记 2025/9/8 20:23:02

再生认证体系有哪些？不同标准对应的要求及可以做的审核机构

再生认证体系 标准 GRS再生回收认证要求 再生原材料的上游企业&#xff1a;需要具备GRS认证证书&#xff0c;以确保原材料的可追溯性和再生成分。 认证条件&#xff1a; 最终商品的再生成分比例必须至少为20%。 只有由至少50%的回收材料制成的产品才能贴上GRS标签。 认证机构…...

编程日记 2025/9/4 8:06:14

[CISSP] [6] 密码学和对称密钥算法

密码学的目标 1. 机密性&#xff08;Confidentiality&#xff09; 目标&#xff1a;保护信息不被未授权访问。 通过 加密&#xff08;Encryption&#xff09;技术确保数据只能被授权方解密和读取。主要方法&#xff1a; 对称加密&#xff08;AES、3DES&#xff09;&#xff…...

编程日记 2025/9/7 1:59:53

thinkphp每条一级栏目中可自定义添加多条二级栏目，每条二级栏目包含多个字段信息

小程序客户端需要展示团购详情这种结构的内容，后台会新增多条套餐，每条套餐可以新增多条菜品信息，每条菜品信息包含菜品名称，价格，份数等字段信息，类似于购物网的商品多规格属性，数据表中以json类型存储，手写了一个后台添加和编辑的demo 添加页面 编辑页面（json数据…...

编程日记 2025/9/9 2:38:50

混杂模式（Promiscuous Mode）与 Trunk 端口的区别详解

一、混杂模式&#xff08;Promiscuous Mode&#xff09; 1. 定义与工作原理 定义&#xff1a;混杂模式是网络接口的一种工作模式&#xff0c;允许接口接收通过其物理链路的所有数据包&#xff0c;而不仅是目标地址为本机的数据包。工作层级&#xff1a;OSI 数据链路层&#x…...

编程日记 2025/9/5 13:31:39

Spring Boot项目信创国产化适配指南

将 Spring Boot 项目适配信创国产化环境&#xff0c;需要从底层基础设施到上层应用组件进行全面替换和调整。以下是主要替换点和适配步骤的总结&#xff1a; 一、基础软件替换 1. JDK 替换 国外JDK&#xff1a;Oracle JDK、OpenJDK国产JDK&#xff1a; 阿里龙井&#xff08;D…...

编程日记 2025/9/4 4:33:53

MySQL：数据类型

数值类型 数值类型用于存储整数、小数、浮点数等&#xff0c;主要分为整数类型和浮点类型。 整数类型 数据类型存储大小取值范围&#xff08;有符号&#xff09;取值范围&#xff08;无符号&#xff09;说明TINYINT1字节-128 ~ 1270 ~ 255小整数&#xff0c;如布尔值&#x…...

编程日记 2025/9/2 8:30:49

maven引入项目内本地包方法

最近在写java实现excel转pdf功能&#xff1b; 网上有个包很好用&#xff0c;免费&#xff1a;spire.xls.free-5.3.0.jar。 但是maven打包项目时报错&#xff0c;找不到这个包。 jar包位置如下&#xff1a; 在项目/src/jar/spire.xls.free-5.3.0.jar。 解决方法&#xff1a…...

编程日记 2025/9/7 5:57:36

ARP协议

ARP协议 ARP协议的作用 当网络设备有数据要发送给另一台网络设备时&#xff0c;必须要知道对方的网络层地址&#xff08;即IP地址&#xff09;。IP地址由网络层来提供&#xff0c;但是仅有IP地址是不够的&#xff0c;IP数据报文必须封装成帧才能通过数据链路进行发送。数据帧…...

编程日记 2025/9/7 11:47:09

科技赋能安居梦：中建海龙以模块化革新重塑城市更新范式

在北京市西城区桦皮厂胡同&#xff0c;一栋始建于上世纪70年代的住宅楼正经历着一场脱胎换骨的蜕变。这座曾被鉴定为D级危房的建筑&#xff0c;在中建海龙科技有限公司&#xff08;以下简称“中建海龙”&#xff09;的匠心打造下&#xff0c;仅用三个月便完成"原拆原建&qu…...

编程日记 2025/8/29 14:33:18

2025 AI智能数字农业研讨会在苏州启幕，科技助农与数据兴业成焦点

4月2日&#xff0c;以"科技助农数据兴业”为主题的2025AI智能数字农业研讨会在苏州国际博览中心盛大启幕。本次盛会吸引了来自全国各地相关部门领导、知名专家学者、行业协会组织&#xff0c;以及县级市农业企业代表、县级市农产品销售商等万名嘉宾齐聚姑苏城&#xff0c;…...

编程日记 2025/9/3 20:48:07

2000-2021年 全国各地区城镇登记失业率数据

全国各地区城镇登记失业率数据2000-2021年.ziphttps://download.csdn.net/download/2401_84585615/90259723 https://download.csdn.net/download/2401_84585615/90259723 城镇登记失业率是衡量地区就业状况的重要指标&#xff0c;反映了在一定时期内&#xff0c;符合就业条件的…...

编程日记 2025/8/29 14:33:16

Cursor的主要好处

以下是Cursor的主要好处&#xff1a; 代码生成与优化 • 快速生成代码&#xff1a;根据简短描述或部分代码片段&#xff0c;Cursor能快速生成完整代码模块&#xff0c;还能智能预测下一步操作&#xff0c;将光标放在合适位置&#xff0c;让开发者一路Tab键顺滑编写代码。 • …...

编程日记 2025/9/8 19:41:16

超便捷语音转文字工具CapsWriter-Offline本地部署与远程使用全流程

文章目录 前言1. 软件与模型下载2. 本地使用测试3. 异地远程使用3.1 内网穿透工具下载安装3.2 配置公网地址3.3 修改config文件3.4 异地远程访问服务端 4. 配置固定公网地址4.1 修改config文件 5. 固定tcp公网地址远程访问服务端 前言 今天给大家安利一个绝对能让你工作效率飙…...

编程日记 2025/9/7 0:11:58

什么是数据仓库

什么是数据仓库 Data warehouse 是面向主题的 主要根据各种数据来源&#xff0c;来进行历史分析 形成一个趋势分析 为数据挖掘、预测建模、机器学习提供基础数据 与传统数据库比如gaussdb的区别。数据仓库注重历史数据分析&#xff0c;guassdb注重实时事务处理 数据仓库时企业的…...

编程日记 2025/9/6 3:55:45

【动态规划】二分优化最长上升子序列

最长上升子序列 II 题解 题目传送门&#xff1a;AcWing 896. 最长上升子序列 II 一、题目描述 给定一个长度为 N 的数列&#xff0c;求数值严格单调递增的子序列的长度最长是多少。 输入格式&#xff1a; 第一行包含整数 N第二行包含 N 个整数&#xff0c;表示完整序列 输…...

编程日记 2025/9/8 2:28:36

MySQL的安装与初始化流程

MySQL概述 MySQL是一个关系型数据库管理系统&#xff0c;由瑞典MySQL AB公司开发&#xff0c;MySQL AB公司被Sun公司收购&#xff0c;Sun公司又被Oracle公司收购&#xff0c;目前属于Oracle公司。 MySQL是目前最流行的关系型数据库管理系统&#xff0c;在WEB应用方面MySQL是最…...

编程日记 2025/9/4 17:13:19

flink standalone集群模式部署

一. 环境准备 1、下载并安装jdk11 2、下载flink 并解压 3、确保服务器之间的免密登录 二、集群搭建 搭建集群至少有三台机器&#xff0c;每台机器的分配角色如下 master: jobManager salve01&#xff1a;taskManager salve02&#xff1a;taskManager 1、在JobManager(…...

编程日记 2025/9/4 11:16:20

Linux线程概念与控制：【线程概念（页表）】【Linux线程控制】【线程ID及进程地址空间布局】【线程封装】

目录 一. 线程概念 1.1什么是线程 1.2分页式存储管理 1.2.1虚拟地址和页表的由来 1.2.2物理内存管理 1.2.3页表 1.2.4页目录结构 1.2.5二级页表地址转换 1.3线程的优点 二.进程VS线程 三.Linux线程控制 3.1POSIX线程库 3.2创建线程 ​编辑 pthread库是个什么东西 …...

编程日记 2025/9/5 22:15:40

7-6 混合类型数据格式化输入

本题要求编写程序&#xff0c;顺序读入浮点数1、整数、字符、浮点数2&#xff0c;再按照字符、整数、浮点数1、浮点数2的顺序输出。 输入格式&#xff1a; 输入在一行中顺序给出浮点数1、整数、字符、浮点数2&#xff0c;其间以1个空格分隔。 输出格式&#xff1a; 在一行中…...

编程日记 2025/9/7 1:30:01

最新全开源码支付系统，赠送3套模板

最新全开源码支付系统&#xff0c;赠送3套模板 码支付是专为个人站长打造的聚合免签系统&#xff0c;拥有卓越的性能和丰富的功能。它采用全新轻量化的界面UI 让您能更方便快捷地解决知识付费和运营赞助的难题&#xff0c;同时提供实时监控和管理功能&#xff0c;让您随时随地…...

编程日记 2025/8/29 10:13:57

Eclipse Leshan 常见问题解答 (FAQ) 笔记

本笔记基于 Eclipse Leshan Wiki - F.A.Q. 页面内容&#xff0c;旨在解答关于 Eclipse Leshan&#xff08;一个开源的 LwM2M 服务器和客户端 Java 实现&#xff09;的常见问题&#xff0c;帮助您更好地理解和使用该工具。 一、Leshan 是什么&#xff0c;我该如何使用它&#x…...

编程日记 2025/8/30 15:09:55

【6】数据结构的栈篇章

目录标题 栈的定义顺序栈的实现顺序栈的初始化入栈出栈获取栈顶元素顺序栈总代码与调试 双端栈的实现双端栈的初始化入栈出栈双端栈总代码与调试 链栈的实现链栈的初始化入栈出栈获取栈顶元素链栈总代码与调试 栈的定义 定义&#xff1a;栈&#xff08;Stack&#xff09;是一种…...

编程日记 2025/9/3 3:32:19

开源虚拟化管理平台Proxmox VE部署超融合

Proxmox VE 是一个功能强大、开源的虚拟化平台&#xff0c;结合了 KVM 和 LXC&#xff0c;同时支持高可用集群、存储管理&#xff08;ZFS、Ceph&#xff09;和备份恢复。相比 VMware ESXi 和 Hyper-V&#xff0c;PVE 具有开源、低成本、高灵活性的特点&#xff0c;适用于中小企…...

编程日记 2025/9/3 5:16:31

C语言基础要素(019)：输出ASCII码表

计算机以二进制处理信息&#xff0c;但二进制对人类并不友好。比如说我们规定用二进制值 01000001 表示字母’A’&#xff0c;显然通过键盘输入或屏幕阅读此数据而理解它为字母A&#xff0c;是比较困难的。为了有效的使用信息&#xff0c;先驱者们创建了一种称为ASCII码的交换代…...

编程日记 2025/9/3 0:26:49

函数柯里化（Currying）介绍（一种将接受多个参数的函数转换为一系列接受单一参数的函数的技术）

文章目录 柯里化的特点示例普通函数柯里化实现使用Lodash进行柯里化 应用场景总结 函数柯里化&#xff08;Currying&#xff09;是一种将接受多个参数的函数转换为一系列接受单一参数的函数的技术。换句话说&#xff0c;柯里化将一个多参数函数转化为一系列嵌套的单参数函数。 …...

编程日记 2025/9/9 1:37:40

基于大模型的主动脉瓣病变预测及治疗方案研究报告

目录 一、引言 1.1 研究背景 1.2 研究目的 1.3 研究意义 二、大模型预测主动脉瓣病变原理 2.1 大模型介绍 2.2 数据收集与处理 2.3 模型训练与优化 三、术前预测与评估 3.1 主动脉瓣病变类型及程度预测 3.2 患者整体状况评估 3.3 手术风险预测 四、术中应用与监测…...

编程日记 2025/9/9 0:48:09

VSCode开发者工具快捷键

自动生成浏览器文件.html的快捷方式 在文本里输入&#xff1a; &#xff01; enter VSCode常用快捷键列表 代码格式化&#xff1a;Shift Alt F向上或向下移动一行&#xff1a;Alt Up 或者 Alt Down快速复制一行代码&#xff1a;Shift Alt Up 或者 Shift Alt Down快速保…...

编程日记 2025/9/8 14:05:10

AI助力PPT制作，让演示变得轻松高效

AI助力PPT制作&#xff0c;让演示变得轻松高效&#xff01;随着科技的进步&#xff0c;AI技术早已渗透到各行各业&#xff0c;特别是在办公领域&#xff0c;AI制作PPT已不再是未来的梦想&#xff0c;而是现实的工具。以前你可能需要花费数小时来制作一个完美的PPT&#xff0c;如…...

编程日记 2025/9/4 21:40:41

行业专家视角下的技术选型与任务适配深度解析

行业专家视角下的技术选型与任务适配深度解析 一、任务属性与技术栈的映射逻辑 &#xff08;1&#xff09;学术类项目需优先考虑技术严谨性、可复现性和理论深度&#xff1a; 机器学习模型开发&#xff1a;PyTorchJupyterMLflow形成完整实验闭环&#xff0c;TensorFlow Exte…...

编程日记 2025/9/7 18:11:55

从零构建大语言模型全栈开发指南：第五部分：行业应用与前沿探索-5.2.1模型偏见与安全对齐（Red Teaming实践）

👉 点击关注不迷路 👉 点击关注不迷路 👉 点击关注不迷路 文章大纲 大语言模型全栈开发指南：伦理与未来趋势 - 第五部分：行业应用与前沿探索5.2.1 模型偏见与安全对齐（Red Teaming实践）一、模型偏见的来源与影响1. 偏见的定义与分类2. 偏见的实际影响案例二、安全对齐…...

编程日记 2025/9/4 3:18:36

JUC系列JMM学习之随笔

JUC: JUC 是 Java 并发编程的核心工具包，全称为 Java Util Concurrent，是 java.util.concurrent 包及其子包的简称。它提供了一套强大且高效的并发编程工具，用于简化多线程开发并提高性能。 CPU核心数和线程数的关系：1核处理1线程（同一时间单次） CPU内核结构： 工作内…...

编程日记 2025/9/2 17:00:21

OpenRouter开源的AI大模型路由工具，统一API调用

简介 ‌OpenRouter是一个开源的路由工具‌&#xff0c;它可以绕过限制调用GPT、Claude等国外模型。以下是对它的详细介绍&#xff1a; 一、主要功能 OpenRouter专注于将用户请求智能路由到不同的AI模型&#xff0c;并提供统一的访问接口。它就像一个“路由器”&#xff0c;能…...

编程日记 2025/9/1 17:54:12

3.9/Q2，Charls最新文章解读

文章题目&#xff1a;Association between remnant cholesterol and depression in middle-aged and older Chinese adults: a population-based cohort study DOI&#xff1a;10.3389/fendo.2025.1456370 中文标题&#xff1a;中国中老年人残留胆固醇与抑郁症的关系&#xff1…...

编程日记 2025/9/5 18:23:34

水下图像增强与目标检测：标签缺失的“锅”？

水下图像增强与目标检测&#xff1a;标签缺失的“锅”&#xff1f; 在水下计算机视觉领域&#xff0c;图像增强和目标检测一直是研究热点。然而&#xff0c;一个有趣的现象引起了研究者的关注&#xff1a;在某些情况下&#xff0c;增强后的水下图像用于目标检测时&#xff0c;…...

编程日记 2025/9/7 18:48:51

从扩展黎曼泽塔函数构造物质和时空的结构-13

得到这些数据到底有什么用呢&#xff1f;无非都是振动&#xff0c;只有频率不同。电性振动和磁性振动的正交环绕关系&#xff0c;本质上只是某个虚数单位的平方倍数&#xff0c; 既然如此&#xff0c;我们就可以考虑&#xff0c;把电和磁当成同一种东西。比如通过改变真空介电常…...

编程日记 2025/9/4 17:57:34

Android学习总结之handler源码级

一、核心类关系与线程绑定&#xff08;ThreadLocal 的核心作用&#xff09; 1. Looper 与 ThreadLocal 的绑定 每个线程的 Looper 实例通过 ThreadLocal<Looper> sThreadLocal 存储&#xff0c;确保线程隔离&#xff1a; public final class Looper {// 线程本地存储&…...

编程日记 2025/9/3 14:15:57

多模态学习（八）：2022 TPAMI——U2Fusion: A Unified Unsupervised Image Fusion Network

论文链接&#xff1a;https://ieeexplore.ieee.org/stamp/stamp.jsp?tp&arnumber9151265 目录 一.摘要 1.1 摘要翻译 1.2 摘要解析 二.Introduction 2.1 Introduciton翻译 2.2 Introduction 解析 三. related work 3.1 related work翻译 3.2 relate work解析 四…...

编程日记 2025/9/8 10:16:54