当前位置：首页 > news >正文

深度学习查漏补缺：4.数据分布的度量

news 来源：原创 2025/5/8 18:43:48

一、数据分布差异的度量

1.KL散度（Kullback-Leibler Divergence）

什么是KL散度？
KL散度是一种用来衡量两个概率分布之间差异的工具。你可以把它想象成一个“距离测量器”，但它不是传统意义上的距离（比如两点之间的直线距离），而是更像在比较两个分布的“相似程度”。简单来说，它告诉你：一个分布（P）有多像另一个分布（Q），或者说要把P“伪装”成Q需要付出多大的代价。

关键词：概率分布、差异、不对称。
本质：KL散度不是对称的，也就是说，P到Q的“距离”和Q到P的“距离”通常不一样。

        用一个生活中的比喻:
        假设你有两个朋友，一个喜欢吃甜食（P分布），另一个喜欢吃辣食（Q分布）。你想让甜食朋友假装成辣食朋友，去骗过一群美食家：
        如果甜食朋友（P）只知道甜品的味道，要模仿辣食朋友（Q）的口味，他需要学习辣椒的味道、麻的口感等等，这个“学习成本”就是KL散度（从P到Q）。
        反过来，如果辣食朋友（Q）要假装成甜食朋友（P），他需要学甜品的甜度和奶油味，这个“学习成本”是另一个KL散度（从Q到P）。
        因为甜食和辣食的差异方向不同，这两个“伪装成本”通常不一样。

KL散度的值越小，说明两个分布越相似；值越大，说明差异越大。

        KL散度的特点:
        1. 非负性：KL散度总是大于等于0。如果等于0，说明两个分布完全一样（P = Q）。
        2. 不对称性：从P到Q的KL散度和从Q到P的KL散度通常不同。就像甜食朋友学辣食和辣食朋友学甜食的难度不一样。
        3. 信息论背景：它来自信息论，可以理解为“用Q来编码P的信息时多花了多少力气”。

        一个简单的例子
        假设你有两袋糖果：
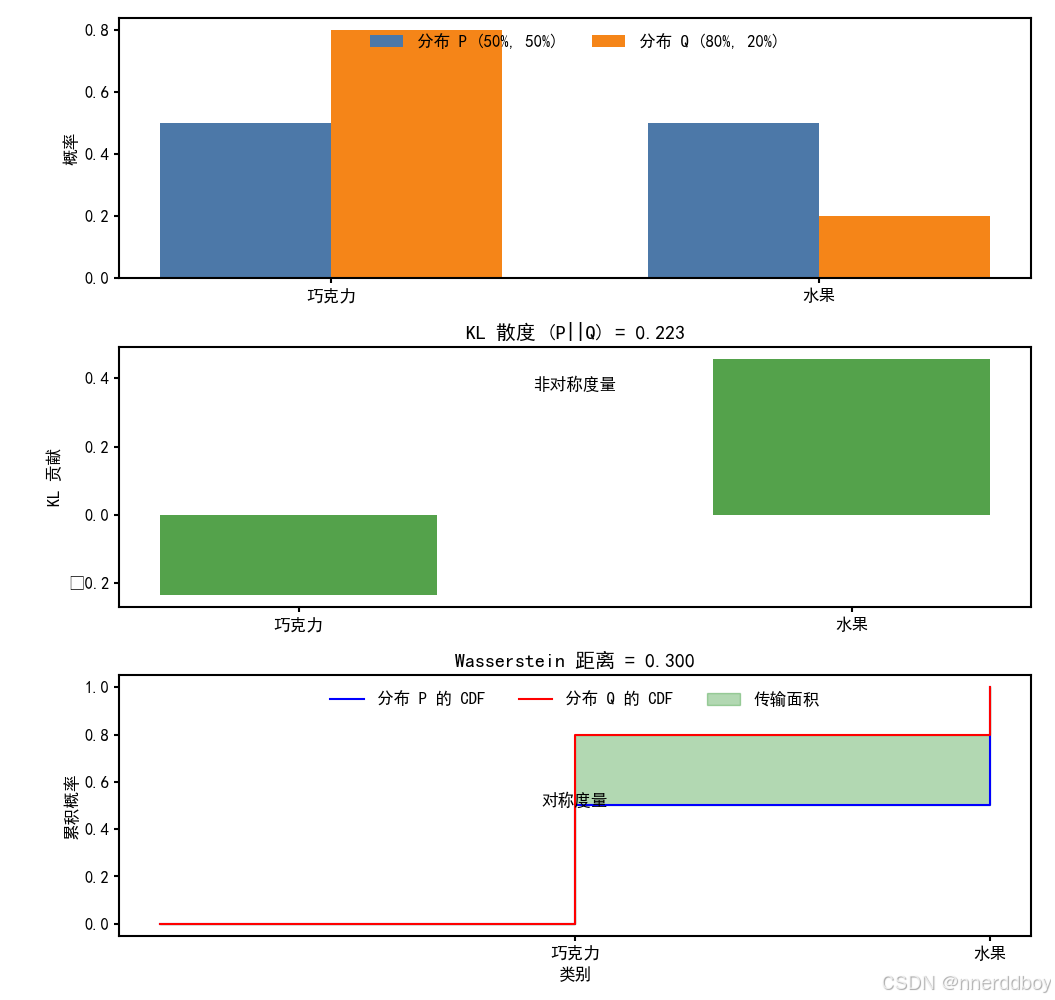
        袋子P：50%巧克力糖，50%水果糖。
        袋子Q：80%巧克力糖，20%水果糖。

        现在你想用袋子Q的分布（80%巧克力，20%水果）去描述袋子P（50%巧克力，50%水果）：
        在P的世界里，水果糖和巧克力糖一样常见，但Q认为水果糖很少。如果你用Q的“眼光”去看P，就会低估水果糖的出现频率。
        KL散度（P到Q）会告诉你：用Q来模拟P有多不靠谱，需要额外调整多少。

反过来，用P去模拟Q（从Q到P），则是另一种调整，因为P会高估水果糖的概率。两种方向的调整成本不同，所以KL散度不对称。

计算KL散度的大致思路：
1. 看P和Q在每个点上的概率。
2. 对每个点，算P的概率除以Q的概率，取对数，再乘以P的概率。
3. 把所有点的结果加起来，就得到了KL散度。

用糖果例子来说，就是比较每个糖果类型（巧克力、水果）的比例差异，再综合起来看总的“伪装难度”。

        总结
        KL散度是个衡量分布差异的工具，像是在问“一个分布假装成另一个分布有多难”。
        它不对称，值越小越相似，等于0时完全一样。
        在你的迁移学习任务中，可以用它挑出跟目标域最像的源域数据，或者优化模型让源域和目标域“看起来更像”。

2.Wasserstein距离

什么是Wasserstein距离？

Wasserstein距离是用来衡量两个概率分布之间差异**的一种方法。你可以把它想象成一个“搬运工”，它的任务是把一个分布的“货物”（概率质量）搬到另一个分布的位置上，而Wasserstein距离就是完成这个搬运工作所需要的最小“总成本”。

关键词：概率分布、搬运、最优成本。
本质：它考虑了分布之间的“几何形状”和“位置关系”，比KL散度更直观地反映分布的实际距离。

        用一个生活中的比喻
        想象你有两个堆沙子：
        堆P：一堆沙子在操场左边。
        堆Q：另一堆沙子在操场右边，距离左边10米。

        你的任务是用铲子把P的沙子搬到Q的位置，变成Q的形状：
        如果P和Q的沙子总量一样（都是1吨），你需要把1吨沙子从左边搬到右边10米。
        搬运的“成本”就是：沙子重量（1吨） × 搬运距离（10米） = 10吨·米。
        这个“最小搬运成本”就是Wasserstein距离。

如果P和Q的形状不同（比如P是尖尖的沙堆，Q是扁平的沙堆），你还需要调整沙子的分布形状，成本会更复杂，但核心还是“搬运距离 × 搬运量”的总和。

       Wasserstein距离的特点:
        1. 对称性：不像KL散度，Wasserstein距离是对称的，从P到Q和从Q到P的距离是一样的（搬沙子从左到右和从右到左成本相同）。
        2. 几何意义：它考虑了分布之间的“空间距离”，更像现实中的直观距离。
        3. 非负性：距离总是大于等于0，如果两个分布完全一样，距离为0。
        4. 搬运计划：它会找到最优的搬运方式，让总成本最小。

        一个简单的例子
        假设有两个商店的苹果库存分布：
        商店P：50%苹果在仓库A，50%在仓库B。
        商店Q：80%苹果在仓库A，20%在仓库B。
        仓库A和仓库B相距10公里。

        你需要把P的苹果分布调整成Q的分布：
        P有50%的苹果在B（0.5个单位），Q只有20%在B（0.2个单位），所以要从B搬0.3个单位的苹果到A。
        搬运成本 = 0.3 × 10公里 = 3公里。
        这里假设总苹果量是1个单位，Wasserstein距离就是3。

这个距离告诉你：要把P变成Q，最少需要搬运3公里·单位的苹果。反过来从Q到P也是一样的成本。

        和KL散度的区别：还记得前面讲的KL散度吗？KL散度像是在比较两个分布的“信息伪装难度”，它不关心分布的空间位置，只看概率值本身。而Wasserstein距离更像“物理搬运”，它会考虑分布的“位置”和“形状”：
        如果两个分布概率值完全一样（比如P和Q都是50% A，50% B），KL散度是0，Wasserstein距离也是0。
        但如果P和Q位置不同（比如P在左边，Q在右边10米），KL散度只看概率值可能觉得差不多，但Wasserstein距离会算上这10米的搬运成本。

        计算Wasserstein距离的大致思路：
        1. 把两个分布想象成两堆沙子。
        2. 找到一种最优的搬运方案：从P的每个点搬多少沙子到Q的每个点。
        3. 计算每条搬运路线的成本（距离 × 搬运量），然后加起来取最小值。

在实际中，计算机用优化算法（比如线性规划）来算这个最小成本。

Wasserstein距离就像一个搬运工，计算把一个分布“搬”成另一个分布的最小成本。
它对称、有几何意义，适合比较分布的位置和形状差异。

Python代码示例：

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import wasserstein_distanceP = np.array([0.5, 0.5])
Q = np.array([0.8, 0.2])
categories = ['巧克力', '水果']eps = 1e-10
P = P + eps; P = P / P.sum()
Q = Q + eps; Q = Q / Q.sum()kl_div = np.sum(P * np.log(P / Q))values = np.array([0, 1])
wasserstein_dist = wasserstein_distance(values, values, P, Q)cdf_P = np.cumsum(P)
cdf_Q = np.cumsum(Q)plt.rcParams.update({'font.family': 'SimHei',  'font.size': 12,'axes.linewidth': 1.5,'lines.linewidth': 1.5,'xtick.major.width': 1.5,'ytick.major.width': 1.5,
})fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(8, 10), sharex=False)# 子图 1：原始分布
x = np.arange(len(categories))
width = 0.35
ax1.bar(x - width/2, P, width, label='分布 P (50%, 50%)', color='#4C78A8')
ax1.bar(x + width/2, Q, width, label='分布 Q (80%, 20%)', color='#F58518')
ax1.set_xticks(x)
ax1.set_xticklabels(categories)
ax1.set_ylabel('概率')
ax1.legend(frameon=False, loc='upper center', ncol=2)# 子图 2：KL 散度的贡献
kl_contribution = P * np.log(P / Q)
ax2.bar(x, kl_contribution, width=0.5, color='#54A24B')
ax2.set_xticks(x)
ax2.set_xticklabels(categories)
ax2.set_ylabel('KL 贡献')
ax2.set_title(f'KL 散度 (P||Q) = {kl_div:.3f}')
ax2.text(0.5, max(kl_contribution)*0.8, '非对称度量', ha='center')# 子图 3：Wasserstein 距离的 CDF 差异
ax3.step([0, 1, 2], [0, *cdf_P], 'b-', label='分布 P 的 CDF', where='post')
ax3.step([0, 1, 2], [0, *cdf_Q], 'r-', label='分布 Q 的 CDF', where='post')
ax3.fill_between([0, 1, 2], [0, *cdf_P], [0, *cdf_Q], step='post', color='green', alpha=0.3, label='传输面积')
ax3.set_xticks([1, 2])
ax3.set_xticklabels(categories)
ax3.set_xlabel('类别')
ax3.set_ylabel('累积概率')
ax3.set_title(f'Wasserstein 距离 = {wasserstein_dist:.3f}')
ax3.text(1, 0.5, '对称度量', ha='center')
ax3.legend(frameon=False, loc='upper center', ncol=3)plt.tight_layout()
plt.show()

深度学习查漏补缺：4.数据分布的度量

一、数据分布差异的度量 1.KL散度（Kullback-Leibler Divergence） 什么是KL散度？ KL散度是一种用来衡量两个概率分布之间差异的工具。你可以把它想象成一个“距离测量器”，但它不是传统意义上的距离（比如两点之…...

编程日记 2025/5/8 18:43:48

银河麒麟V10 aarch64架构安装mysql教程

国产操作系统 ky10.aarch64 因为是arm架构，故选择mysql8，推荐安装8.0.28版本尝试8.0.30和8.0.41版本均未成功，原因不明☹️ 1. 准备工作 ⏬ 下载地址：https://downloads.mysql.com/archives/community/ 2. 清理历史环境不用管…...

编程日记 2025/5/8 18:02:48

【NLP 52、多模态相关知识】

生活应该是美好而温柔的，你也是 —— 25.4.1 一、模态 modalities 常见： 文本、图像、音频、视频、表格数据等罕见： 3D模型、图数据、气味、神经信号等二、多模态 1、Input and output are of different modalities (eg： tex…...

编程日记 2025/5/8 18:08:49

[NCTF2019]Fake XML cookbook [XXE注入]

题目源代码 function doLogin(){var username $("#username").val();var password $("#password").val();if(username "" || password ""){alert("Please enter the username and password!");return;}var data "…...

编程日记 2025/4/29 17:29:49

I²C总线高级特性与故障处理分析

IC总线高级特性与故障处理深度分析目录 1. IC基础回顾 1.1 IC通信基本原理1.2 IC总线时序与协议1.3 寻址方式与读写操作 2. IC高级特性 2.1 多主机模式2.2 时钟同步与伸展2.3 高速模式与Fast-mode Plus2.4 10位寻址扩展 3. IC总线故障与锁死 3.1 断电锁死原理3.2 总线挂起与…...

编程日记 2025/5/8 18:38:15

【力扣hot100题】（039）二叉树的直径

这题在简单题中有点难度，主要是不要把边数和深度搞混（我就这样）。我想了很久，发现如果当前节点没有右节点，就将它的右长度设为0，左节点同理，并且在递归是不会加一，而是将加一的操作…...

编程日记 2025/5/8 18:06:54

L2-001 紧急救援

注意题目没有说边的数量，实际最多有5e5条边，开小了第四个样例会错！！！ - 思路: Dijkstra 求最短路并且维护路径条数和最大人数。 #include<bits/stdc.h> using namespace std;typedef pair<int, int> pii…...

编程日记 2025/5/8 17:59:28

分组背包问题

与01背包的区别是，多了一个限制条件，将物品打包，每组物品只能用一个 #include <iostream> #include <algorithm>using namespace std;const int N 110;int v[N][N], w[N][N], s[N]; int f[N]; int n, m;int main() {cin >>…...

编程日记 2025/5/8 17:31:19

【工业场景】用YOLOv12实现饮料类别识别

饮料类别识别任务的意义在于帮助人们更快速地识别和区分不同类型的饮料，从而提高消费者的购物体验和满意度。对于商家而言，饮料类别识别可以帮助他们更好地管理库存、优化货架布局和预测销售趋势，从而提高运营效率和利润。此外，饮…...

编程日记 2025/5/8 18:28:45

宽带空时波束形成算法原理及MATLAB仿真

宽带阵列信号处理空时波束形成、空时波束形成方向图卫星导航空时抗干扰算法 MATLAB仿真文章目录前言一、空时波束形成结构二、空时波束形成方向图三、MATLAB仿真四、MATLAB源代码总结前言 \;\;\;\;\; 空时波束形成（Space-Time Beamforming）是一种结…...

编程日记 2025/5/8 17:19:50

406. 根据身高重建队列

链接 406. 根据身高重建队列 - 力扣（LeetCode） 题目思路可能的一个思路是先对高的人进行处理，这样后面插入矮的人时不会影响高的人的位置。比如，如果先处理高个子，那么当插入一个矮个子的时候，前面的高…...

编程日记 2025/5/8 17:35:58

机器学习：人工智能的核心驱动力

近年来，机器学习（Machine Learning，简称ML）已成为人工智能（AI）领域的核心驱动力。它不仅广泛应用于图像识别、自然语言处理、医疗诊断等领域，还推动了自动驾驶、智能推荐系统等前沿技术的发展。…...

编程日记 2025/5/8 17:18:24

机器视觉中的传统视觉与深度视觉

工业视觉是现代制造业中一个非常重要的应用领域，广泛用于产品质量检测，尤其是在生产线上。几乎所有的工业产品在流入市场之前，都要经历严格的缺陷检测环节，以确保它们符合质量标准。而在这一过程中，工业视觉检测系统发…...

编程日记 2025/5/8 17:12:01

机器学习开发全流程详解：从数据到部署的完整指南

机器学习项目的成功不仅依赖算法选择，更在于系统化的开发流程。本文详细拆解各阶段的核心任务、工具及注意事项，并通过表格总结帮助开发者快速掌握关键要点。 1. 数据获取与准备数据是机器学习的基础，需确保数据的质量与代表性。关键任务…...

编程日记 2025/5/4 17:42:12

春晚魔术[蓝桥]

这里考虑到N很大则快速幂无法处理，因为它并没有被取模欧拉定理： 当是质数时是质数两边同时取mod， // // Created by yumo_ // #include<bits/stdc.h>using namespace std; #define scin std::cin #define scout std::cout using …...

编程日记 2025/5/5 3:14:26

CF580B Kefa and Company（滑动窗口）

题目描述 Sergei B., the young coach of Pokemons, has found the big house which consists of n flats ordered in a row from left to right. It is possible to enter each flat from the street. It is possible to go out from each flat. Also, each flat is connecte…...

编程日记 2025/5/4 4:23:11

多模态RAG实践：如何高效对齐不同模态的Embedding空间？

目录多模态RAG实践：如何高效对齐不同模态的Embedding空间？ 一、为什么需要对齐Embedding空间？ 二、常见的对齐方法与关键技术点 （一）对比学习（Contrastive Learning） （二&#…...

编程日记 2025/5/8 17:22:47

linux 时钟

chronyc sourcestats 查看所有的源以及那个比较稳定 chronyc tracking 查看当前使用的是那个 ntpstat synchronised to NTP server (119.28.183.184) at stratum 3 time correct to within 57 ms polling server every 1024 s chronyc tracking | grep "Reference ID&quo…...

编程日记 2025/5/8 15:31:21

【leetcode100】每日温度

1、题目描述给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。示例 1: 输…...

编程日记 2025/5/5 17:50:47

华为交换综合实验——VRRP、MSTP、Eth-trunk、NAT、DHCP等技术应用

一、实验拓扑二、实验需求 1,内网Ip地址使用172.16.0.0/16分配 2,sw1和SW2之间互为备份 3, VRRP/STP/VLAN/Eth-trunk均使用 4,所有Pc均通过DHCP获取IP地址 5,ISP只能配置IP地址 6,所有电脑可以正常访问IsP路由器环回三、需求分析 1、设备连接需求二层交换机（LS…...

编程日记 2025/5/5 13:29:54

边缘检测技术现状初探2:多尺度与形态学方法

一、多尺度边缘检测方法多尺度边缘检测通过在不同分辨率/平滑度下分析图像，实现： 粗尺度（大σ值）：抑制噪声，提取主体轮廓细尺度（小σ值）：保留细节，检测微观…...

编程日记 2025/5/6 3:28:38

【JavaScript】十四、轮播图

文章目录实现一个轮播图，功能点包括： 自动播放鼠标经过暂时播放鼠标离开继续播放点击切换按钮手动切换 div盒子嵌套先写出静态HTML，再使用JS来修改样式和数据，渲染页面： <!DOCTYPE html> <html lang"…...

编程日记 2025/5/7 9:20:07

19信号和槽_信号和槽的基本概念

①Linux 信号 Signal 是系统内部的通知机制. 是进程间通信的方式 （给进程发信号kill命令，像情景内存泄漏，管道一端关闭另一端还是读，会给进程发信号） ②信号三要素信号源: 谁发的信号信号的类型: 哪种类别的信号信…...

编程日记 2025/4/29 23:06:26

云端革命：数字文明的重构与新生

引言：算力大爆炸时代 2023年，当ChatGPT在全球掀起AI狂潮时，很少有人意识到，支撑这场智能革命的正是背后庞大的云计算基础设施。每天，全球云计算平台处理的数据量超过500EB，相当于5亿部高清电影&#xff1b…...

编程日记 2025/5/7 15:10:58

论文阅读笔记：Denoising Diffusion Implicit Models （4）

0、快速访问论文阅读笔记：Denoising Diffusion Implicit Models （1） 论文阅读笔记：Denoising Diffusion Implicit Models （2） 论文阅读笔记：Denoising Diffusion Implicit Models &#xff08…...

编程日记 2025/5/4 22:51:10

红帽Linux怎么重置密码

完整流程 ●重启操作系统，进入启动界面 ●然后按进入选择项界面 ●找到linux单词开头的那一行，然后移动到该行末尾（方向键移动或者使用键盘上的end），在末尾加入rd.break ●按ctrl x进入rd.break模式 ●在该模式下依次…...

编程日记 2025/5/5 1:27:10

关于存储的笔记

存储简介名称适用场景常见运用网络环境备注块存储高性能、低延迟数据库局域网专业文件存储数据共享共享文件夹、非结构化数据局域网通用对象存储大数据、云存储网盘、网络媒体公网（断点续传、去重）海量存储协议名称协议块存储FC-SAN或IP-SAN承载的…...

编程日记 2025/5/6 12:43:16

java根据集合中对象的属性值大小生成排名

1：根据对象属性降序排列 public static <T extends Comparable<? super T>> LinkedHashMap<T, Integer> calculateRanking(List<ProductPerformanceInfoVO> dataList, Function<ProductPerformanceInfoVO, T> keyExtractor) {Linked…...

编程日记 2025/5/6 15:39:31

蓝桥杯嵌入式16届—— LED模块

使用主板是STMG431RBT6 STMG431RBT6资源资源配置表跳线说明表引脚状况 PC8~PC15分别对应着LD1~LD8 SN74HC573ADWR 是一种锁存器当 LE（锁存使能）为高电平，输出 Q 实时跟随输入 D 的变化。当 LE 为低电平，输出锁定为最后…...

编程日记 2025/5/7 14:34:11

【IOS webview】源代码映射错误，页面卡住不动

报错场景 safari页面报源代码映射错误，页面卡住不动。机型：IOS13 技术栈：react 其他IOS也会报错，但不影响页面显示。 debug webpack配置不要GENERATE_SOURCEMAP。解决方法： GENERATE_SOURCEMAPfalse react-app…...

编程日记 2025/4/30 22:24:08

206. 反转链表 92. 反转链表 II 25. K 个一组翻转链表

leetcode Hot 100系列文章目录一、翻转链表二、反转链表 II三、K 个一组翻转链表总结一、翻转链表建立pre为空，建立cur为head，开始循环：先保存cur的next的值，再将cur的next置为pre，将pre前进到cur的位置&#xf…...

编程日记 2025/5/6 17:09:14

绘制动态甘特图（以流水车间调度为例）

import matplotlib.pyplot as plt import matplotlib.animation as animation import numpy as np from matplotlib import cm# 中文字体配置（必须放在所有绘图语句之前） plt.rcParams[font.sans-serif] [SimHei] plt.rcParams[axes.unicode_minus] Fa…...

编程日记 2025/5/8 7:21:15

生成式AI应用带来持续升级的网络安全风险

生成式AI应用带来持续升级的网络安全风险概要根据Netskope最新研究，企业向生成式AI（GenAI）应用共享的数据量呈现爆炸式增长，一年内激增30倍。目前平均每家企业每月向AI工具传输的数据量已达7.7GB，较一年前的250MB实现…...

编程日记 2025/5/5 23:52:52

C++17更新内容汇总

C17 是 C14 的进一步改进版本，它引入了许多增强特性，优化了语法，并提升了编译期计算能力。以下是 C17 的主要更新内容： 1. 结构化绑定（Structured Bindings） 允许同时解构多个变量，从 std::tup…...

编程日记 2025/5/6 7:51:43

conda activate激活环境失败问题

出现 CondaError: Run conda init before conda activate 的错误，通常是因为 Conda 没有正确初始化当前的命令行环境。以下是解决方法： 1. 初始化 Conda 运行以下命令以初始化 Conda： conda init解释： conda init 会修改当前 S…...

编程日记 2025/4/29 11:23:35

TensorFlow实现逻辑回归

目录前言TensorFlow实现逻辑回归前言实现逻辑回归的套路和实现线性回归差不多, 只不过逻辑回归的目标函数和损失函数不一样而已. TensorFlow实现逻辑回归 import tensorflow as tf import numpy as np import matplotlib.pyplot as plt from sklearn.datasets import mak…...

编程日记 2025/5/5 21:04:51

第十四届蓝桥杯大赛软件赛省赛Python 大学 C 组：6.棋盘

题目1 棋盘小蓝拥有 nn 大小的棋盘，一开始棋盘上全都是白子。小蓝进行了 m 次操作，每次操作会将棋盘上某个范围内的所有棋子的颜色取反(也就是白色棋子变为黑色，黑色棋子变为白色)。请输出所有操作做完后棋盘上每个棋子的颜色。输入格…...

编程日记 2025/5/5 0:10:13

电商场景下高稳定性数据接口的选型与实践

在电商系统开发中，API接口需要应对高并发请求、动态数据更新和复杂业务场景。我将重点解析电商场景对数据接口的特殊需求及选型方案。一、电商API必备的四大核心能力千万级商品数据实时同步支持SKU基础信息/价格/库存多维度更新每日增量数据抓取与历史版本对比…...

编程日记 2025/5/6 23:29:17

内网服务器centos7安装jdk17

1. 下载 JDK 17 安装包（在外网环境操作） 在可联网的机器上下载 JDK 17 的压缩包（推荐使用 OpenJDK）： OpenJDK 官方源： Adoptium Eclipse Temurin Azul Zulu 直接下载命令示例（在外网机器上执行…...

编程日记 2025/5/1 8:29:12

Git 使用教程

Git 使用教程 Git 是目前最流行的分布式版本控制系统，它能够高效地管理代码，并支持团队协作开发。本文将介绍 Git 的基本概念、常用命令以及如何在实际项目中使用 Git 进行版本控制。 1. Git 基本概念在使用 Git 之前，需要了解以下几个基…...

编程日记 2025/5/5 0:24:24

【无标题】跨网段耦合器解决欧姆龙CJ系列PLC通讯问题案例

欧姆龙CJ系列PLC不同网段的通讯问题一、项目背景某大型制造企业的生产车间内，采用了多台欧姆龙CJ系列PLC对生产设备进行控制。随着企业智能化改造的推进，需要将这些PLC接入工厂的工业以太网，以便实现生产数据的实时采集、远程监控以及与企业…...

编程日记 2025/5/2 3:57:03

13_pandas可视化_seaborn

导入库 import numpy as np import pandas as pd # import matplotlib.pyplot as plt #交互环境中不需要导入 import seaborn as sns sns.set_context({figure.figsize:[8, 6]}) # 设置图大小 # 屏蔽警告 import warnings warnings.filterwarnings("ignore")关系图 …...

编程日记 2025/5/5 2:29:39

【C++进阶四】vector模拟实现

目录 1.构造函数（1）无参构造（2）带参构造函数（3）用迭代器构造初始化函数（4）拷贝构造函数 2.operator= 3.operator[] 4.size() 5.capacity() 6.push_back 7.reserve 8.迭代器（vector的原生指针） 9.resize 10.pop_back 11.insert 12.erase 13.memcpy…...

编程日记 2025/4/27 11:14:41

14使用按钮实现helloworld(1)

目录还可以通过按钮的方式来创建 hello world 涉及Qt 中的信号槽机制本质就是给按钮的点击操作,关联上一个处理函数当用户点击的时候就会执行这个处理函数 connect（谁发的信号， 信号类型， 谁来处理这个信息， 怎么处理的&…...

编程日记 2025/5/6 21:25:39

嵌入式EMC设计面试题及参考答案

目录解释 EMC（电磁兼容性）的定义及其两个核心方面（EMI 和 EMS）电磁兼容三要素及相互关系为什么产品必须进行 EMC 设计？列举至少三个实际工程原因分贝（dB）在 EMC 测试中的作用是什么？为何采用对数单位描述干扰强度？传导干扰与辐射干扰的本质区别及典型频率范围…...

编程日记 2025/4/30 2:40:13

cursor的.cursorrules详解

文章目录 1. 文件位置与作用2. 基本语法规则3. 常用规则类型与示例3.1 忽略文件/目录3.2 限制代码生成范围3.3 自定义补全建议3.4 安全规则 4. 高级用法4.1 条件规则4.2 正则表达式匹配4.3 继承规则 5. 示例文件6. 注意事项 Cursor 是一款基于 AI 的智能代码编辑器，…...

编程日记 2025/5/7 5:58:59

Opencv计算机视觉编程攻略-第七节提取直线、轮廓和区域

第七节提取直线、轮廓和区域 1.用Canny 算子检测图像轮廓2.用霍夫变换检测直线；3.点集的直线拟合4.提取连续区域5.计算区域的形状描述子图像的边缘区域勾画出了图像含有重要的视觉信息。正因如此，边缘可应用于目标识别等领域。但是简单的二值边缘分布图…...

编程日记 2025/5/6 10:02:38

清明假期在即

2025年4月2日，6~22℃，一般遇见的事：这么都是清明出去玩？你们不扫墓的么。感受到的情绪：当精力不放在一个人身上，你就会看到很多人，其实可以去接触的。反思：抖音上那么多不幸和幸…...

编程日记 2025/5/6 19:54:15

数字孪生技术解析：开启虚拟与现实融合新时代

一、数字孪生技术的概念与原理数字孪生技术是一种通过构建物理对象的数字映射，实现虚拟与现实同步的技术。该技术集成了物联网、云计算、人工智能、大数据等多种前沿技术，能够对物理世界进行全方位的仿真和管理。在数字孪生技术中，物理建模…...

编程日记 2025/5/5 17:50:50

Docker Registry 清理镜像最佳实践

文章目录 registry-clean1. 简介2. 功能3. 安装 docker4. 配置 docker5. 配置域名解析6. 部署 registry7. Registry API 管理8. 批量清理镜像9. 其他10. 参考 registry-clean 1. 简介 registry-clean 是一个强大而高效的解决方案，旨在简化您的 Docker 镜像仓库管理…...

编程日记 2025/5/7 17:19:06

一、数据分布差异的度量

1.KL散度（Kullback-Leibler Divergence）

2.Wasserstein距离

相关文章：