论文解读:《Word embedding factor based multi-head attention》——基于词嵌入因子的多头注意力
原文链接:Word embedding factor based multi-head attention | Artificial Intelligence Review
多头注意力机制线性地将查询、键和值投影到不同的子空间中,允许模型从不同的角度理解输入序列,并利用输入句子序列中有关令牌之间关系的信息。
Transformer、Bert等基于多头注意力机制的深度学习模型存在两个问题:
第一,头的数量总是手动设置的,并且不清楚在面对新的NLP任务时,我们应该设置多少头才能达到最佳性能。
第二,当这些头将自注意力机制中的查询、键和值投影到不同的子空间时,它们的实际意义缺乏合理的解释。
多头注意力机制的改进:
1.引入了分歧正则化来多样化注意力分布,增强了模型捕获不同特征的能力。
2.提出了一种改进多头协作的方法,这表明当前的方法可能无法充分利用不同头的协作潜力。
3.提出了动态组合多头注意力机制(DCMHA ),通过动态组合注意力头来增加模型的表达能力。
这些方法主要通过改进位置编码、通道和空间压缩以及信息传递机制来提高多头注意力,从而提高Transformer或BERT等模型的性能和效率。然而,它们并没有解决注意力头数量的自动选择和注意力机制的可解释性问题。
针对上述问题,本文提出一种新的注意力机制——基于因子分析的多头注意力机制。
首先,在自注意力机制计算过程之前,对输入的词向量进行因子分析。通过语言模型获得的预训练词嵌入已经包含了关于单词的句法和语义信息,而因子分析可以用来识别嵌入矩阵所有维度之间的可能关系。
第二,多头注意力中的头数可以根据因子分析中确定的公因子个数来确定。此外,自注意力机制中的查询、键和值可以根据公共因子和原始词嵌入维度之间的对应关系进行识别。
第三,我们为查询、键和值设计了一种新的线性投影方法,在使用较少参数的情况下,在实践中取得了有竞争力的性能。通过我们的方法和后续的投影规则得到的查询、键和值与典型的多头注意力机制相比,在语义上更加聚焦,具有更强的可解释性。
最后,类似于典型的多头注意力机制,将每个头计算得到的新表达式合并作为输出。该方法可以用于任何使用自注意力机制的NLP任务。在本文中,我们将说明使用BERT作为背景的方法,因为它在其架构中使用了自注意力机制。
因子分析是一种从一组变量中提取公共因子的统计方法,可分为两类:验证性因子分析和探索性因子分析。验证性因素分析通常用于检验变量与因素之间关系的预定假设,而探索性因素分析在没有预定假设的情况下,探索可能存在的关系并提取公因子。
因子分析的目的与主成分分析类似, 要把多个变量的信息压缩到少数几个变量中, 压缩的结果称为“因子”, 因子需要起到把变量分组的作用。
模型架构
该模型的整体架构与BERT等基于Transformer编码器的模型一致。输入数据首先经过一个词嵌入层,得到每个视图的初始嵌入向量。然后经过注意力层,注意力层由多头注意力机制和基于位置的全连接前馈网络组成。注意力层由N个相同的层堆叠而成。每层有两个子层。第一种是本文提出的FAM Attention层,第二种与传统框架相同。我们还在两个子层的周围使用了一个残差连接,然后使用层归一化。最后,通过线性层得到输出。

子图( 2 )说明了FAM 注意力机制。这里的S - D Attention表示尺度化的点积注意力
FAM注意力机制
使用预训练的词向量模型(Word2vec、Glove2vec),可以正常地初始化词嵌入层中的参数,并以微调的方式帮助训练整个语言模型。这些WVM产生的词嵌入向量被认为在一定程度上具有表示相关句子的一些句法和语义信息的能力。从一个特定的词向量机中得到一个词嵌入向量矩阵W =
,其中k是词汇量的大小,d是嵌入维数,我们假设d维向量可以从不同的角度来表示每个词的含义。作者通过对W进行探索性因子分析来考察d个维度之间潜在的相似关系,从而对词向量表示有更深入的理解。
探索性因子分析尝试识别出基础变量(或称因子)来解释在一组观察到的变量中体现的相关模式。因子分析通常用于数据降维,其目的是识别出少数几个因子来解释大多数在众多显性变量中所观测到的方差。因子分析也可用于生成关于因果机制的假设或过滤变量以用于随后的分析。
BERT 中的典型多头注意力涉及将查询、键和值线性地投影到h个不同的子空间中,以学习来自h个不同视图的输入表示。如果输入数据是句子对,这些输入是由词嵌入,位置编码和额外段嵌入的加法和产生的。h是多头注意力机制中的头数,通常手动设置为8,12或16。作者通过应用因子分析结果来决定头的个数,并得到这h个不同的子空间,这比规范的手动设置更具有实际意义。
词嵌入的语义分解
为确定词头个数及其对应的维度,采用因子分析法对词嵌入的所有维度进行降维分解。首先,需要对词嵌入矩阵W进行巴特利特的球型检验和KMO检验,以检验W是否适合做因子分析。因子分析模型的拟合方法主要有3种:极小残差算法 、最大似然法和主成分分析法 ( PCA ) 。在这项研究中,选择了PCA,因为它可以很容易地计算W的特征值和公因子的累积方差贡献。PCA在实际实验中也有较快的计算速度。对于h < d个公共因子的因子分析的代数表示见下面的公式:

式中:Wi表示原始词嵌入矩阵的第i维向量,i = 1,2,· · ·,d;Fj表示公因子,j = 1,2,..,h;ei表示Wi的具体因子;Vi ( j )表示权重,表示Wi与公共因子fj相关联的程度,即因子载荷。
头的个数通过如下结果决定:
首先,计算W的协方差矩阵为C,并对C的特征值进行降序排序;
其次,观察特征值的下降趋势,找出特征值开始下降的点。在实际中,我们识别这种下降的标准是基于一个明确且自动的标准:当当前特征值与下一个特征值的差值小于上一个特征值与当前特征值的差值时,我们选择"头"的数量。这个概念类似于因子分析中的碎石图,曲线斜率开始趋于平缓的点意味着向特征值差异逐渐减小的过渡。其数学表达式为eh - e(h + 1 )< e(h - 1) - eh,其中eh表示按降序排列的第h个特征值。此时,将公共因子数h设为该点特征值的累加数;
第三,利用PCA对W进行因子分析,将公共因子设置为h,得到d个维度与h个因子的对应关系,即每个维度属于哪个因子。
查询、键和值的不同投影
作者采用了一种精细的线性投影设计,使得模块能够对输入信息获得更深入的理解。这不同于典型自注意力中的多传感头注意力,它直接将整个输入投影到相同大小的不同子空间中。根据上一节因子分析的结果,得到了由原始词嵌入矩阵X分解得到的h个成分{ c1,c2,· · ·,ch }:

其中,Disassemble ( X )函数是指对输入矩阵X进行因子分析,b是批次大小,l是序列长度,len_fi是fi的长度。fi表示一个列表{ di1,di2,· · ·,dlen _ fi i },其中fi中的len_fi维度属于第i个公因子。显然,fi的长度之和等于d,如下式所示。

然后将聚合的h部分进行单独的缩放点积自注意力:

式中:qi∈Rlen _ fi * len _ fi、ki∈Rlen _ fi * len _ fi和vi∈Rlen _ fi * len _ fi均为可学习的线性投影矩阵,其大小由fi的长度决定。最后,将输出c′1,c′2,· · ·,c′h按照X中d维的原始相对顺序组合在一起。
![]()
如图2所示,相同颜色的尺寸表示它们属于一个相同的公因子,而不同特定颜色打印的所有d维尺寸属于不同的公因子,这应该与因子分析结果一致。属于同一公因子的尺寸在拆卸过程中合并在一起。在实现新颖的FAM注意力机制后,在合并过程中所有维度都恢复到原来的位置。

其中b表示批大小,l表示序列长度,d表示每个嵌入的长度。
S-D Attention表示尺度化的点积注意力
算法进阶的理论阐释
因子分析的本质可以理解为将相关的维度聚为一类,将相关性较小的维度分离出来,相当于根据嵌入的语义进行聚类。
传统的多头注意力通过线性投影将整个嵌入映射到相同大小的几个子空间,相当于将嵌入的所有维度平均分配。
作者的方法在应用线性投影之前先对输入进行因子分析,类似于从语义角度对嵌入维度进行聚类。
方差常用来衡量信息的不确定性或信息的混乱程度。
作者的方法得到的类内偏差平方和Var(X)小于或等于传统方法得到的类内偏差平方和Var(Xold):
![]()
计算Q、K、V的过程实质上是对原始矩阵的一次线性变换。作者的方法Q、K、V的参数矩阵大小比传统方法小,经过线性变换后,数据的总方差会更小。
![]()
作者的方法得到的方差比传统方法的小,信息混淆程度更低,提高了模型的学习有效性。
传统多头注意力中的参数总数为:
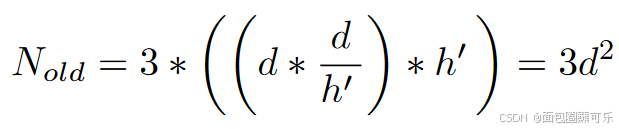
作者提出的新型自注意力机制中的可学习参数总数为:

比较得到如下结果:
![]()
注意力机制包括三个步骤:
( 1 )将输入投影到子空间,( 2 )自注意力和( 3 )级联后的最终投影。
表1比较了每个步骤的FAM层和典型多头注意力层的计算复杂度。

复杂度的差异仅在于从步骤( 1 )开始的线性投影,即矩阵乘法的底层。
选取的公因子个数的影响
由PCA理论可知,增加主成分的个数会导致更多信息被保留。

(b)显示了我们的方法在不同数量的注意力头下的性能,使用FAM Attention块对所有模型进行处理。
横轴表示公共因子(头数),纵轴表示对应注意力头数的模型预测准确率。
随着公共因子个数的增加,模型性能有所提升,但提升程度随着公共因子个数的变大而减小。
当词嵌入的长度一定时,较大数量的注意力头导致从原始变量中提取的因子保留的信息量更大,导致这些因子表达的语义子空间更细致、更鲜明。由这些注意力头计算得到的新词嵌入更加准确。

增加注意力头的数量虽然可以提高模型精度,但也会导致计算效率降低。因此,为了在有效性和效率之间取得平衡,不能无限制地增加头数。
相关文章:

论文解读:《Word embedding factor based multi-head attention》——基于词嵌入因子的多头注意力
原文链接:Word embedding factor based multi-head attention | Artificial Intelligence Review 多头注意力机制线性地将查询、键和值投影到不同的子空间中,允许模型从不同的角度理解输入序列,并利用输入句子序列中有关令牌之间关系的信息。…...

单片机和微控制器知识汇总——《器件手册--单片机、数字信号处理器和可编程逻辑器件》
目录 四、单片机和微控制器 4.1 单片机(MCU/MPU/SOC) 一、定义 二、主要特点 三、工作原理 四、主要类型 五、应用领域 六、选型与设计注意事项 七、发展趋势 4.2 数字信号处理器(DSP/DSC) 编辑编辑 一、定义 二、工作原理 三、结构特点 四、应用领域 五、选型与设计注…...
——48.旋转图像)
LeetCode hot 100 每日一题(15)——48.旋转图像
这是一道难度为中等的题目,让我们来看看题目描述: 给定一个 n n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。 你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。 提示…...

Java多线程精讲:线程操作与状态转换全解析
前言 本章内容为作者结合学习与实践的总结整理,虽力求准确,但疏漏之处在所难免。若有任何疑问或建议,恳请读者朋友们不吝指正,共同完善知识体系,感激不尽! 一、认识多线程(Thread&#…...

HashMap的位操作是什么?HashSet 的 contains 方法复杂度是多少?红黑树简单讲一下?
一、HashMap 的位操作设计 HashMap 使用位运算优化哈希计算与索引定位,核心场景如下: 哈希扰动函数 计算键的哈希值时,将高16位与低16位异或: static final int hash(Object key) {int h;return (key null) ? 0 : (h key.hash…...

GitHub开源的容器管理面板-Dpanel
dpanel Docker安装部署二进制部署 GitHub官网 一块轻量化docker可视化管理面板,由国人开发,个人觉得是比较好用的,功能都很齐全,并且可以通过修改源码,自定义前端样式等。 Docker安装部署 官网 部署环境࿱…...

vue-将组件内容导出为Word文档-docx
1. 安装依赖 首先,我们需要安装docx库,以便在前端生成Word文档。可以通过以下命令进行安装: npm install docx 2. 实现导出功能 2.1 初始化文档 使用docx库创建一个新的文档实例,并定义文档的结构和内容。我们使用Document、…...

IMX6ULL学习篇——系统学习设备树
IMX6ULL学习篇——系统学习设备树 这篇博客的目的是系统的整理一下设备树当中的一些非常基本的概念。基于之前的学习,我们已经至少掌握了字符设备的基本的框架,编写一个最简单的字符设备简单的流程。 但是我们知道,一个外设很有可能是…...

使用vector构造杨辉三角形
力扣118题: 给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。 在「杨辉三角」中,每个数是它左上方和右上方的数的和。 示例 1: 输入: numRows 5 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]示例 2: 输入: numRows 1…...

亮数据爬取API爬取亚马逊电商平台实战教程
前言 在当今数据驱动的商业环境中,企业需要快速、精准地获取互联网上的公开数据以支持市场分析、竞品调研和用户行为研究。然而,传统的手动网页爬取方式面临着诸多挑战:IP封锁、验证码干扰、网站结构频繁变更,以及高昂的运维成本…...

AI+金融 应用 使用DeepSeek、Qwen等大模型输入自然语言,得到通达信等行情软件公式代码,导入后使用
AI金融 应用 使用DeepSeek、Qwen等大模型输入自然语言,得到通达信等行情软件公式代码,导入后使用。不会编程,也能行情软件中实现个性化条件选股,个性化技术指标。 AIbxm低估值趋势选股策略,参考提示词: 编…...

SmolVLM2: 让视频理解能力触手可及
一句话总结: SmolVLM 现已具备更强的视觉理解能力📺 SmolVLM2 标志着视频理解技术的根本性转变——从依赖海量计算资源的巨型模型,转向可在任何设备运行的轻量级模型。我们的目标很简单: 让视频理解技术从手机到服务器都能轻松部署。 我们同步发布三种规…...

去中心化金融
什么是去中心化金融 去中心化金融(Decentralized Finance,简称 DeFi)是一种基于区块链技术构建的金融系统,旨在通过去除传统金融机构(如银行、证券公司等)作为中介,提供各种金融服务。这些服务…...

Mysql并发事务带来哪些问题?
大家好,我是锋哥。今天分享关于【Mysql并发事务带来哪些问题?】面试题。希望对大家有帮助; Mysql并发事务带来哪些问题? 1000道 互联网大厂Java工程师 精选面试题-Java资源分享网 在 MySQL 中,事务并发执行时会引发一系列问题,…...

PCL 点云多平面探测
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 Open3D为我们提供了一种点云多平面探测的算法,该算法使用基于鲁棒统计的方法进行平面补丁检测。该算法具体过程:首先将点云细分为更小的块(使用二分法),然后尝试为每个点云块匹配一个平面。如果平面通过了鲁棒平…...

OpenBMC:BmcWeb添加路由5 设置handler函数
对路由对象完成了权限和method的设置后,最重要的就是设置路由的处理函数: //http\routing\taggedrule.hpptemplate <typename... Args> class TaggedRule :public BaseRule,public RuleParameterTraits<TaggedRule<Args...>> {...template <typename F…...
---损失(loss) 准确率(accuracy)问题)
攻破tensorflow,勇创最佳agent(2)---损失(loss) 准确率(accuracy)问题
实战播: 怎么判定一个模型好不好,你设置的值对不对? 需要再看几个值: 例如: model Sequential()for units in model_structure:model.add(Dense(units, activationrelu))model.add(Dropout(train_config.get(dropout_rate, 0.3)))model.add(Dense(1, activationsigmoid)) 他…...

括号合法题
一、括号合法题 2116. 判断一个括号字符串是否有效 //采用从左往右和从右往左遍历的贪心算法,分别保证前缀合法,后缀合法。public boolean canBeValid(String s, String locked) {int ns.length();if (n%21) return false;int num0;// 从左到右扫描&…...

C++11之深度理解lambda表达式
前言 在现代C中,Lambda表达式提供了一种简洁而强大的方式来定义匿名函数,使代码更具可读性和灵活性。自C11引入Lambda以来,它已经成为STL算法、并发编程和回调机制中的重要工具。随着C14、C17和C20的不断演进,Lambda的功能也在不断…...

字符串常量,数组和指针的不同形式
在 C 语言中,字符串 "hello" 存储在内存中是一个字符数组,它的内存布局通常如下: 1. 字符串常量区: 字符串常量(如 "hello")是存储在程序的数据段(通常称为 .data 或 .ro…...

全面讲解python的uiautomation包
在常规的模拟鼠标和键盘操作,我们一般使用pyautogui,uiautomation模块不仅能直接支持这些操作,还能通过控件定位方式直接定位到目标控件的位置,而不需要自己去获取对应坐标位置。uiautomation模块不仅支持任意坐标位置截图&#x…...

性能测试笔记
8、JMeter扩展开发 扩展组件开发的意义 输入参数协议复杂调用逻辑功能等等 开发前的工具准备 下载jdk并安装,配置环境变量下载maven,配置环境变量修改settings.xml本地仓库,远程仓库的地址Eclipse新建Maven项目编辑 pom.xml Maven常用命令…...

相对位置2d矩阵和kron运算的思考
文章目录 1. 相对位置矩阵2d2. kron运算 1. 相对位置矩阵2d 在swin-transformer中,我们会计算每个patch之间的相对位置,那么我们看到有一连串的拉伸和相减,直接贴代码: import torch import torch.nn as nntorch.set_printoptio…...
)
从C语言开始的C++编程生活(2)
前言 本系列文章承接C语言的学习,需要有C语言的基础才能学会哦~ 第2篇主要讲的是有关于C的缺省参数和函数重载。 C才起步,都很简单呢! 目录 前言 缺省参数 基本语法 缺省参数的作用 函数重载 基本语法 重载的作用 缺省参数 缺省参数…...
)
【设计模式】深入解析装饰器模式(Decorator Pattern)
深入解析装饰器模式(Decorator Pattern) 一、装饰器模式的核心概念 装饰器模式是一种结构型设计模式,用于动态地给对象添加新功能,而不改变其原始代码。 1. 为什么需要装饰器? 避免继承带来的类爆炸问题࿱…...
)
K8S集群新增和删除Node节点(K8s Cluster Adds and Removes Node Nodes)
实战:在已有K8S集群如何新增和删除Node节点 在Kubernetes (K8S) 集群中,Node节点是集群中的工作节点,它们运行着容器的实际实例。管理K8S集群中的Node节点,包括新增和删除节点,是一个常见且重要的操作,可以…...

2503C++,C++标准的执行
最优雅的应该是c26刚刚引入的std::execution,通过sender/receiver模型和常用的异步算法来简化调用异步逻辑,还可随时改成协程. #include <stdexec/execution.hpp> #include <exec/static_thread_pool.hpp> int main() {exec::static_thread_pool pool(3);auto sch…...

nodejs中实现一个自定义的require方法
1.前言 大家对nodejs中的require方法应该不会陌生,这个方法可以用来导入nodejs的内置模块,自定义模块,第三方模块等,使用频率非常高,那么这个方法内部是如何实现的呢?本篇文章就是从头到尾拆分实现流程,最终实现一个自定义的require方法的 2.前置操作 导入所需的nodejs内置…...

vscode/cursor中python运行路径设置 模块导入问题
vscode/cursor中python运行路径设置 ## 文件路径设置 问题描述 pycharm的项目用cursor运行,出现目录找不到 后来利用 os.getcwd(),经过打印调试发现是IDE的本身配置问题 pycharm中,os.getcwd()默认打开当前脚本所在目录 vscode/cursor中…...
)
Spring学习笔记05——Spring Boot的文件结构2(POJO类)
在Spring Boot项目中,将Entity、DTO、VO放在POJO子模块中是一种常见的分层设计,它们各自承担不同的职责,通过一个通俗的例子来解释它们的作用: POJO(Plain Old Java Object)是指普通的、简单的Java对象&am…...
)
html和css 实现元素顺时针旋转效果(椭圆形旋转轨迹)
一 实现效果 二 实现代码 我自己是用react写的。 1. react 代码如下: import React from "react"; import styles from "./index.less";export default () > {return <div className{styles.containers}><div className{styles.c…...

C# 的Lambda表达式常见用法和示例
C# 的 Lambda 表达式是一种强大的语法糖,能够极大简化代码并增强灵活性。以下是它的主要功能和应用场景,结合具体示例说明: 1. 简化委托实例化 Lambda 可以快速定义委托(如 Func、Action),无需显式…...

2024年数维杯数学建模C题天然气水合物资源量评价解题全过程论文及程序
2024年数维杯数学建模 C题 天然气水合物资源量评价 原题再现: 天然气水合物(Natural Gas Hydrate/Gas Hydrate)即可燃冰,是天然气与水在高压低温条件下形成的类冰状结晶物质,因其外观像冰,遇火即燃&#…...

Qt中10倍提升动态截屏及渲染60帧/秒
Qt中10倍提升动态截屏及渲染60帧/秒 理解模态窗口和非模态窗口 在C中,窗口的**模态(Modal)和非模态(Modeless)**显示是两种不同的对话框或窗口行为模式,主要区别体现在用户交互和程序流程控制上。以下是它…...

OpenCV 基础全方位剖析:夯实计算机视觉开发根基
在计算机视觉的广袤领域中,OpenCV 是一座极为关键的里程碑。无论是在前沿的学术研究,还是在蓬勃发展的工业界,OpenCV 凭借其强大的功能与高效的性能,为开发者提供了丰富的图像处理和计算机视觉算法,助力无数项目落地。…...

Java试题
试题: 解析 1-5: 5: 6: 7: 8: 9: 10: 11: 12: 13:...

基于 arco 的 React 和 Vue 设计系统
arco 是字节跳动出品的企业级设计系统,支持React 和 Vue。 安装模板工具 npm i -g arco-cli创建项目目录 cd someDir arco init hello-arco-pro? 请选择你希望使用的技术栈React❯ Vue? 请选择一个分类业务组件组件库Lerna Menorepo 项目❯ Arco Pro 项目看到以…...

解密细胞衰老与溶解:AbMole助力胰腺癌研究新突破
近日,一项由德国罗斯托克大学医学中心的研究团队完成的研究,在探索胰腺癌细胞衰老与溶解的复杂机制上取得了重要进展。这项研究不仅深化了我们对胰腺癌生物学特性的理解,更为未来的研究开辟了新的方向。而在这场科学探索中,AbMole…...

罗德与施瓦茨FSU8,频谱分析仪
罗德与施瓦茨FSU8频谱分析仪 R&S FSU系列频谱仪是动态范围、相位噪声、电平精度和分辨率带宽等频谱仪指标,所有这些指标也是用户设计、测量和生产下一代无线通讯元件的重要保障。出色的表现能力 频率范围:从20Hz开始,分别到3.6 GHz, 8…...

【零基础JavaScript入门 | Day7】三大交互案例深度解析|从DOM操作到组件化开发
【零基础JavaScript入门 | Day7】三大交互案例深度解析|从DOM操作到组件化开发 🌟今日知识图谱: ✅ 事件驱动编程 → 按钮交互与定时器控制 ✅ 组件化思维 → 可复用UI模块开发 ✅ 用户体验优化 → 动画与状态反馈设计 ✅ 工程化实践 → 代码…...

[BalticOI 2009] Radio Transmission 无线传输
题目来自洛谷网站: KMP思路: 结论:n - ne[n] 模拟样例,如下图所示: 代码: #include<bits/stdc.h> #define int long long using namespace std; const int N 1e620;int n; char s[N]; int ne[N];…...
—— 部署 Cloudflare Pages 和 Cloudflare Workers)
SvelteKit 最新中文文档教程(10)—— 部署 Cloudflare Pages 和 Cloudflare Workers
前言 Svelte,一个语法简洁、入门容易,面向未来的前端框架。 从 Svelte 诞生之初,就备受开发者的喜爱,根据统计,从 2019 年到 2024 年,连续 6 年一直是开发者最感兴趣的前端框架 No.1: Svelte …...

32位汇编:MASM32环境搭建与汇编窗口程序
引言 “汇编语言”是计算机底层的编程语言,直接操作硬件资源。32位汇编相比16位汇编在寄存器宽度、内存寻址和指令集等方面有了显著提升。本文将带你从零开始搭建32位汇编开发环境,并编写第一个窗口程序。 1. 环境搭建 1.1 下载MASM32 MASM32是一个专门…...

如何在 `php-fpm` 启动后自动运行自定义命令
如何在 php-fpm 启动后自动运行自定义命令 在使用 php-fpm 时,有时需要在 php-fpm 启动后自动运行一些自定义命令,例如启动一个 Web 应用程序。本文将详细介绍如何通过 systemd 的 ExecStartPost 指令实现这一功能,并记录解决过程中遇到的问…...
)
26考研——图_图的代码实操(6)
408答疑 文章目录 五、图的代码实操图的存储邻接矩阵结构定义初始化插入顶点获取顶点位置在顶点 v1 和 v2 之间插入边获取第一个邻接顶点获取下一个邻接顶点显示图 邻接表结构定义初始化图插入顶点获取顶点位置在顶点 v1 和 v2 之间插入边获取第一个邻接顶点获取下一个邻接顶点…...

栈资源释放示例
import java.util.EmptyStackException; /** * 栈资源释放示例类 * 栈资源在编程中通常指两种概念:1) 内存中的调用栈空间(存储方法调用和局部变量),由系统自动管理 * 2) 自定义的栈数据结构(如链表实现的栈对象&…...

【Qt 01】cmake搭建Qt VS2019开发环境
文章目录 准备第一步:安装Qt5 库第二步:编写CMakeLists.txt第三步:编写批处理文件其他配置Qt VS Toolsqt 源码调试配置 疑问初始的.ui, .qrc文件如何生成? 准备 编码:vscode debug: vs2019 Qt vs Tools 插件 c包管理…...

余弦退火算法与学习率预热
余弦退火算法与学习率预热 总述: (1)标准余弦退火算法(Cosine Annealing)是通过单次的余弦曲线调整学习率,在一个周期内让学习率从一个最大值平滑下降η_max到最小值η_min,这种调整模式是非周…...

ref vs reactive,watch vs watchEffect的区别与使用场景
一、ref 与 reactive 的核心区别 使用场景 ref:处理基本数据类型;需要重新赋值对象(如从api获取新数据) reactive:处理复杂的嵌套对象或者数组,不需要整体替换,直接访问属性(避免频繁写.value&…...

SQLark SQL编辑器秘籍,编写高效SQL查询
SQLark 是一款功能强大的数据库开发和管理工具,用于快速查询、创建和管理不同类型的数据库系统,支持达梦、Oracle 和 MySQL 数据库。SQLark内置的 SQL 编辑器,基于语法解析,集成智能提示、实时语法检查及语法高亮等功能࿰…...
