当前位置：首页 > news >正文

前馈神经网络 - 参数学习（优化问题）

news 来源：原创 2025/8/19 5:44:34

神经网络的参数学习比线性模型要更加困难，主要原因有两点:（1)非凸优化问题和（2)梯度消失问题，本文我们来学习和分析这两类问题。

一、非凸优化问题

1、非凸优化问题演示：

神经网络的优化问题是一个非凸优化问题。

以一个最简单的 1-1-1 结构的两层神经网络为例：

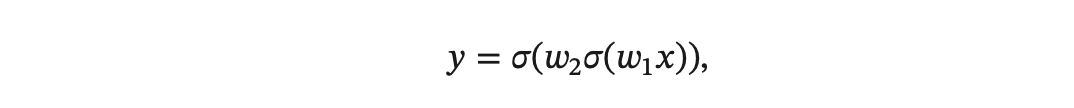
其中 𝑤1 和 𝑤2 为网络参数，𝜎(⋅) 为 Logistic 函数。

给定一个输入样本 (1, 1)，分别使用两种损失函数，第一种损失函数为平方误差损失:L(𝑤1, 𝑤2) = (1 − 𝑦)^2，第二种损失函数为交叉熵损失 L(𝑤1, 𝑤2) = log 𝑦。

当 𝑥 = 1, 𝑦 = 1 时，其平方误差和交叉熵损失函数分别为:L(𝑤1, 𝑤2) = (1 − 𝑦)^2 和 L(𝑤1, 𝑤2) = log 𝑦。

损失函数与参数 𝑤1 和 𝑤2 的关系如下图所示，可以看出两种损失函数都是关于参数的非凸函数。

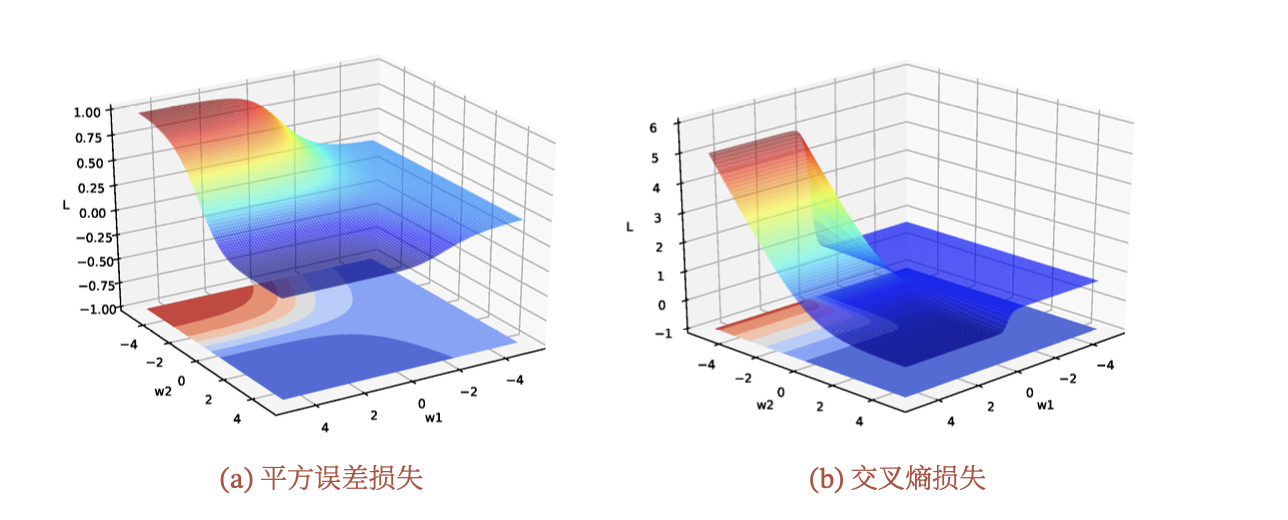
2、关于非凸优化问题的进一步理解

神经网络的参数优化涉及非凸优化问题，这是由于其损失函数的高维性和非线性结构导致的复杂地形。以下是逐步解释：

损失函数的非凸性：
- 非线性激活函数：如ReLU、sigmoid等激活函数引入了非线性，导致损失函数无法保持凸性。
- 多层结构：深度神经网络的多层叠加进一步增强了非线性，使损失函数呈现多个局部极小值和鞍点。
局部极小值与鞍点：
- 局部极小值：高维空间中存在大量局部最优解，梯度下降可能陷入其中。
- 鞍点：在高维空间中，鞍点数量远多于局部极小值，梯度接近零，导致优化停滞。
优化挑战：
- 初始化敏感性：不同参数初始化可能导致收敛到不同解，合理的初始化（如He、Xavier）有助于找到良好起点。
- 梯度消失/爆炸：深层网络中梯度可能因连乘效应变得极小或极大，影响参数更新。
应对策略：
- 优化算法改进：
  - 动量法：引入动量项加速收敛并减少震荡。
  - 自适应学习率：如Adam、RMSProp，动态调整学习率以适应不同参数。
- 正则化技术：如Dropout、权重衰减（L2正则化），防止过拟合并平滑损失函数。
- 批量归一化：加速训练并减少对初始化的敏感度。
- 随机性引入：小批量梯度下降的噪声有助于逃离局部最优。
高维空间的特性：
- 宽谷现象：许多局部极小值在损失值上接近，实际中任一均可接受。
- 鞍点逃离：高维空间中，梯度下降结合动量可有效逃离鞍点。
实际表现与理论差异：
- 尽管理论上是非凸的，实践表明深度神经网络可通过上述方法有效训练，暗示损失函数可能存在有利结构（如平坦区域）。

总结：神经网络的非凸优化虽具挑战，但通过算法改进、正则化及高维空间特性，仍能高效训练模型。关键在于利用经验策略缓解非凸性带来的困难，而非追求全局最优。

二、梯度消失问题

1、梯度消失问题演示：

在神经网络中误差反向传播的迭代公式为：

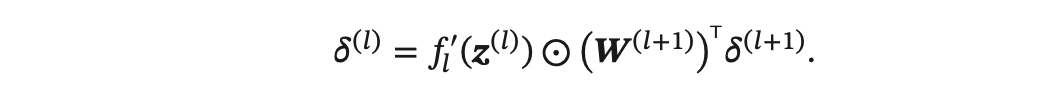
误差从输出层反向传播时，在每一层都要乘以该层的激活函数的导数。当我们使用 Sigmoid 型函数:Logistic 函数 𝜎(𝑥) 或 Tanh 函数时，其导数为：

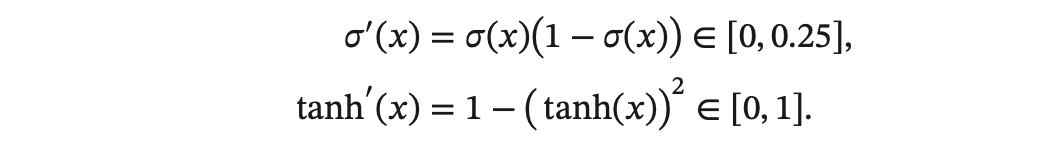
Sigmoid 型函数的导数的值域都小于或等于 1，如下图所示：

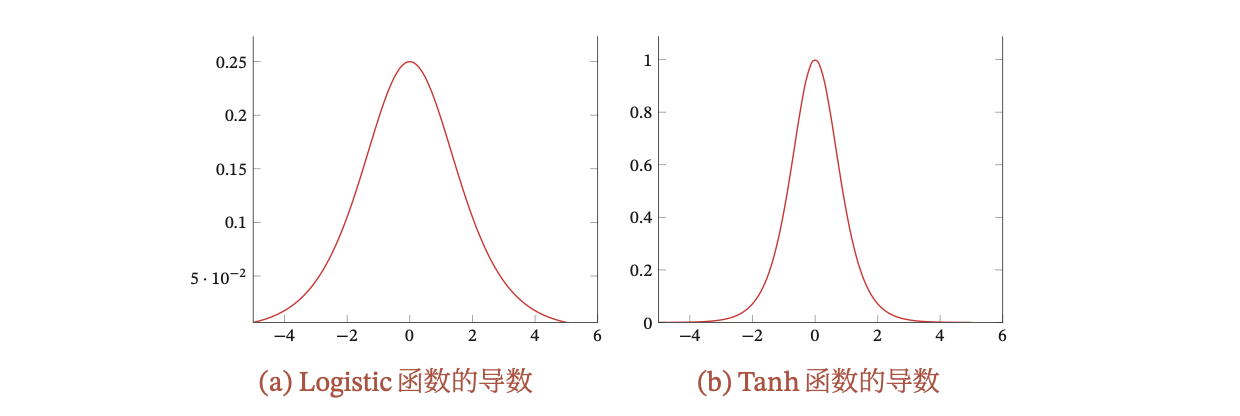
由于 Sigmoid 型函数的饱和性，饱和区的导数更是接近于 0。这样，误差经过每一层传递都会不断衰减。当网络层数很深时，梯度就会不停衰减，甚至消失，使得整个网络很难训练。这就是所谓的梯度消失问题(Vanishing Gradient Problem)，也称为梯度弥散问题。

在深度神经网络中，减轻梯度消失问题的方法有很多种。一种简单有效的方式是使用导数比较大的激活函数，比如 ReLU 等。

2、进一步理解梯度消失问题

如何理解神经网络的参数优化过程中的梯度消失问题？

梯度消失（Vanishing Gradient）是神经网络训练中常见的问题，尤其在深层网络中更为突出。它表现为反向传播过程中，靠近输入层的参数梯度变得极小甚至趋近于零，导致这些参数无法有效更新，网络难以学习到有效的特征表示。以下从原因、数学解释、影响及解决方案四部分详细分析。

（一）梯度消失的原因

激活函数的选择
使用 Sigmoid 或 Tanh 等饱和型激活函数时，其导数在输入较大或较小时会趋近于零。例如：
- Sigmoid 的导数最大值为 0.25（当输入为 0 时），随着输入远离 0，导数迅速衰减。
- Tanh 的导数最大值为 1（输入为 0 时），但在输入较大时也会趋近于零。
后果：反向传播时，梯度需要逐层乘以激活函数的导数，导致梯度指数级衰减。
深层网络的链式法则放大效应
假设网络有 LL 层，反向传播时梯度需通过链式法则逐层相乘：

（二）数学示例：梯度消失的量化分析

（三）梯度消失的影响

浅层参数无法更新
靠近输入层的参数梯度趋近于零，导致网络无法学习到输入数据的底层特征（如边缘、纹理等）。
网络收敛缓慢或停滞
参数更新幅度极小，损失函数下降缓慢，甚至陷入局部极值。
模型性能受限
深层网络的优势无法发挥，模型可能退化为浅层网络的效果。

（四）解决方案

使用非饱和激活函数
- ReLU（Rectified Linear Unit）：
  
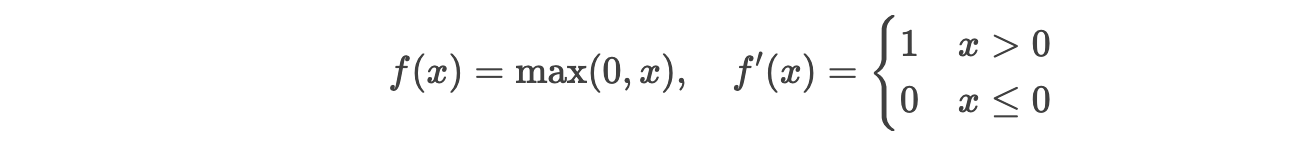
  在正区间导数为 1，避免了梯度衰减，但需注意“神经元死亡”问题（负区间梯度为 0）。
- Leaky ReLU：
  
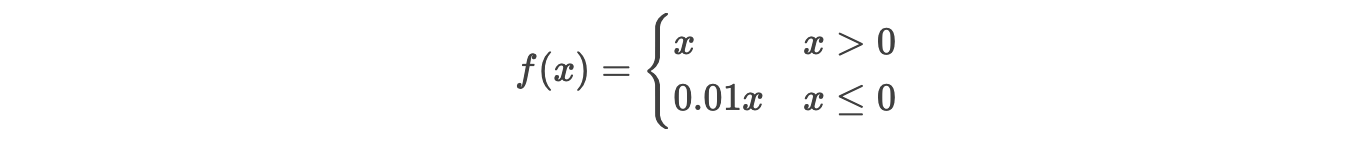
  负区间保留微小梯度，缓解神经元死亡问题。
残差连接（ResNet）
引入跳跃连接（Skip Connection），将输入直接传递到深层：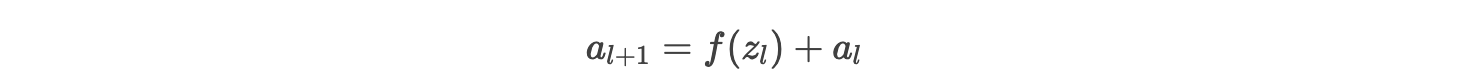

作用：梯度可通过跳跃连接直接回传，绕过非线性变换，避免梯度消失。
批量归一化（Batch Normalization）
对每层输入进行标准化：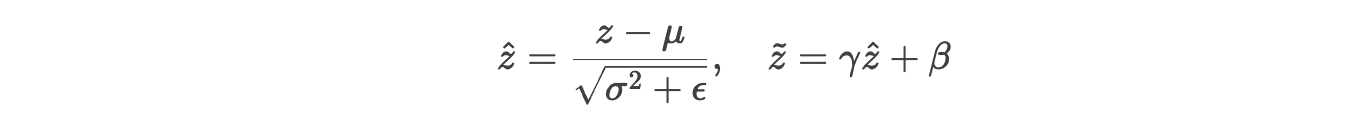

作用：稳定输入分布，减少激活函数饱和概率，间接缓解梯度消失。
梯度裁剪与自适应优化器
- 梯度裁剪：限制梯度幅值，防止梯度爆炸（与梯度消失问题相关）。
- Adam、RMSProp：自适应调整学习率，对不同参数使用不同的更新幅度，提升稳定性。
参数初始化策略
- Xavier 初始化：根据输入输出维度调整初始权重范围，避免激活值过早饱和。
- He 初始化：专为 ReLU 设计，初始权重方差为 2/n2/n，其中 nn 为输入维度。

（五）实际案例

问题场景：训练一个 10 层全连接网络时，发现前 3 层的权重几乎不更新，损失函数下降缓慢。
诊断：检查各层梯度，发现输入层梯度接近零，中间层梯度逐渐增大。
解决方案：

将 Sigmoid 激活函数替换为 ReLU。
加入残差连接，允许梯度直接回传。
使用 He 初始化参数。
结果：输入层梯度显著增大，模型收敛速度加快，准确率提升。

总结

梯度消失的根源在于激活函数的导数过小与深层链式法则的乘积效应，导致浅层梯度衰减。通过替换激活函数、引入残差结构、批量归一化等方法，可有效缓解这一问题。实际应用中需结合网络深度、任务需求选择合适的策略，确保梯度稳定传播，充分发挥深层网络的表达能力。